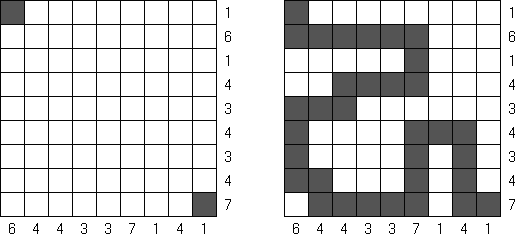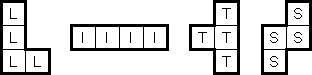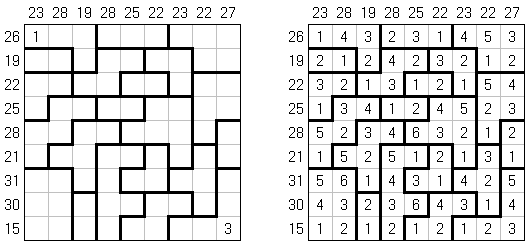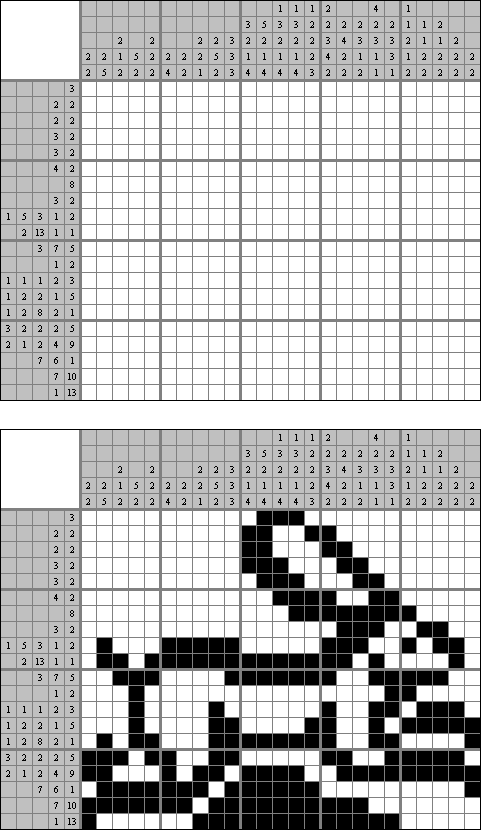
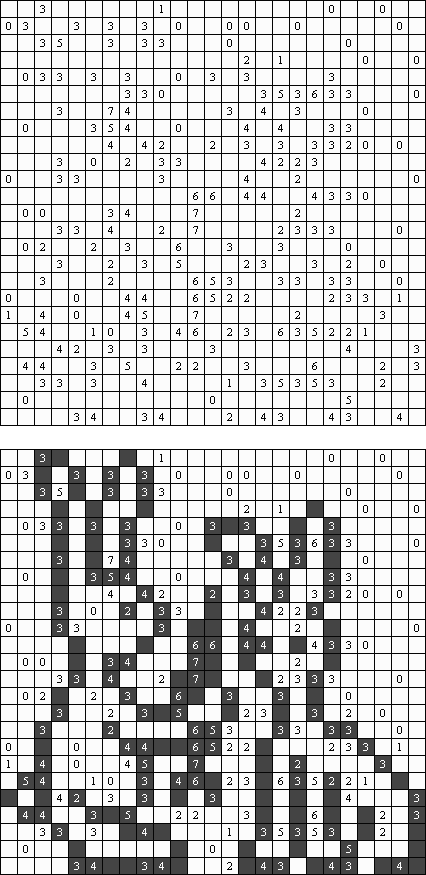
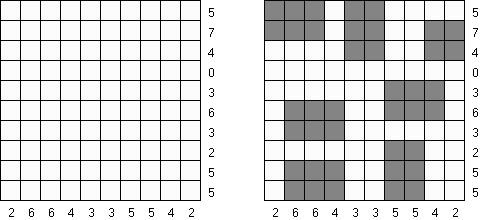
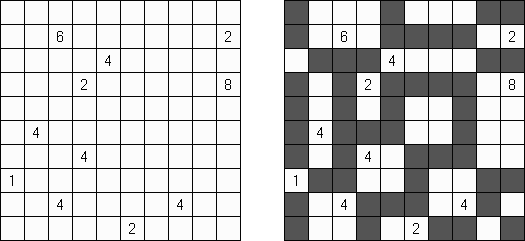
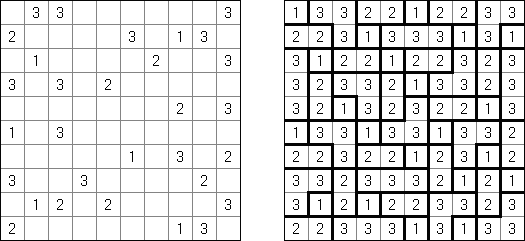
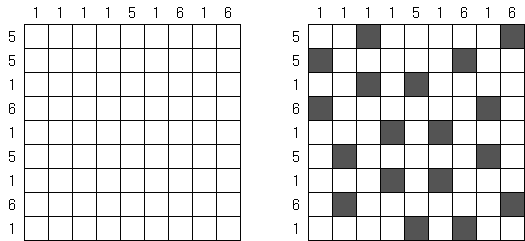
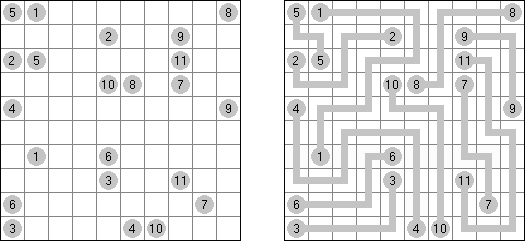
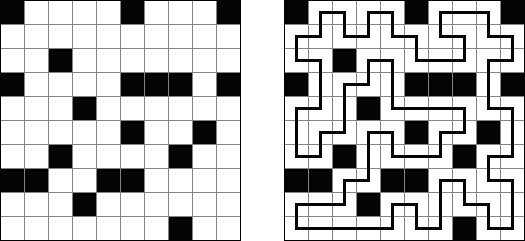
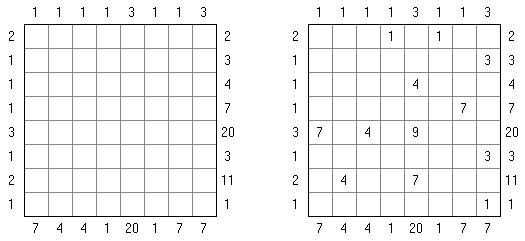
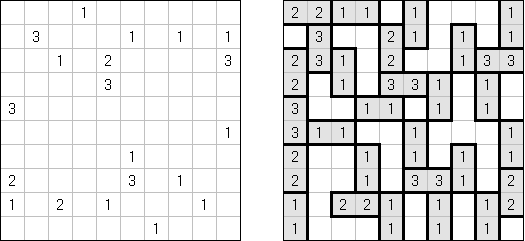
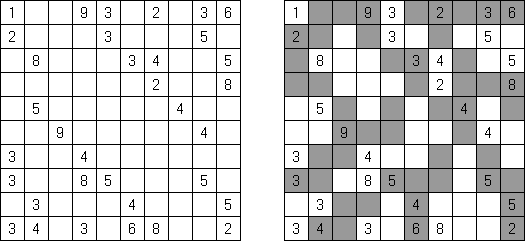
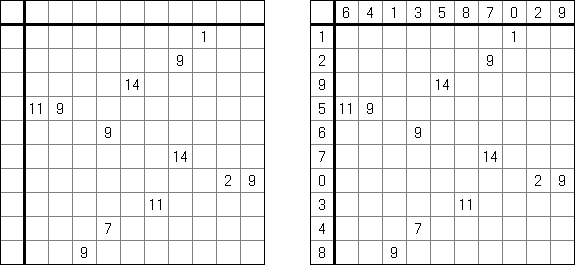
Cross+A パズル

Cross+Aは様々な種類のパズルを解く。プログラムはパズルの作成のバッチモードを利用できる仕様になっている。

判じ絵（ののぐらむ、イラストロジック、ピクロスともいう；英語：Nonogram、Paint By Numbers、Griddler、CrossPix、Hanjie）とは、ヒント数字を使い、正方形または長方形の中に絵をかくパズルである。1個の数字は、連続して黒く塗り潰すマス目の数を表している。そして、同じ列の数字は各黒マスのグループでの黒マスの数を表している。グループの間、少なくとも1白マスがある。

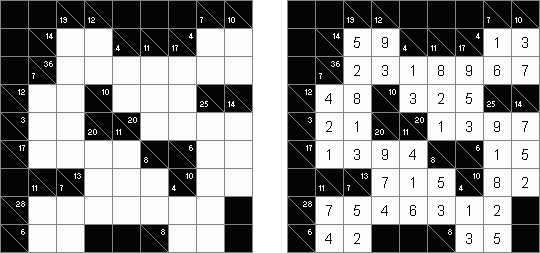
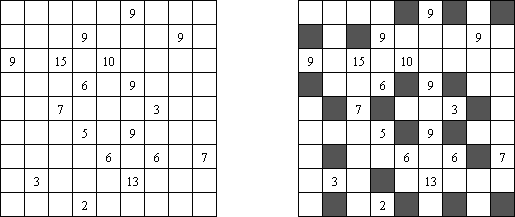
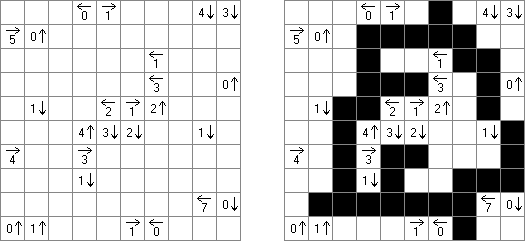
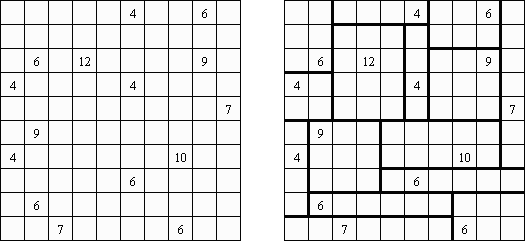
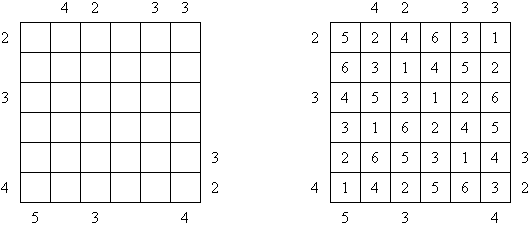
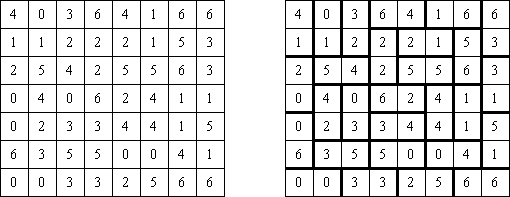
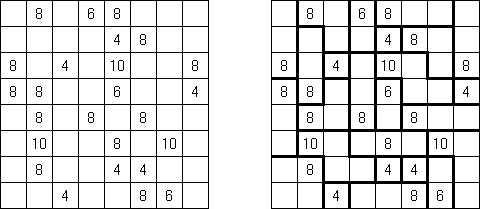
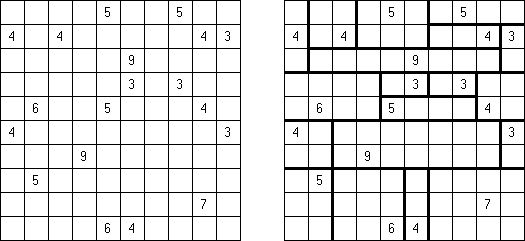
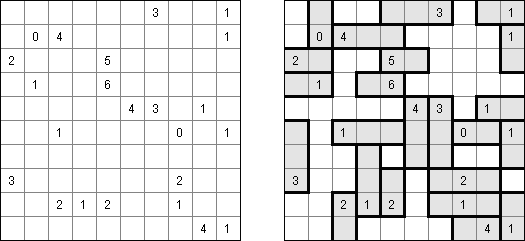
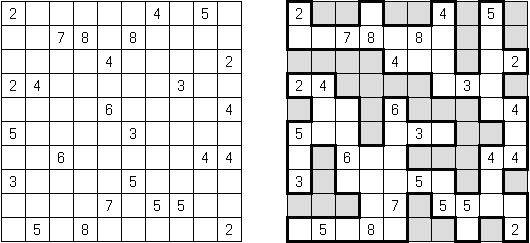
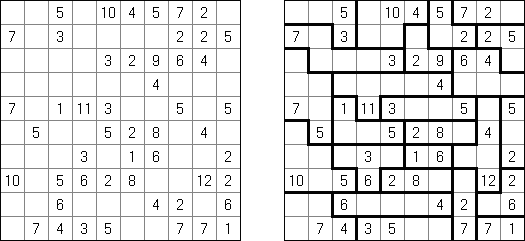
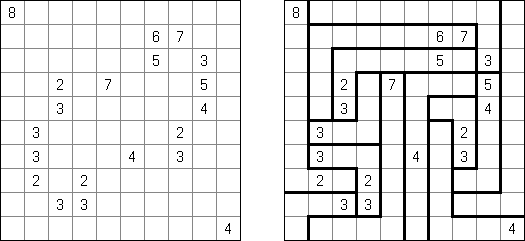
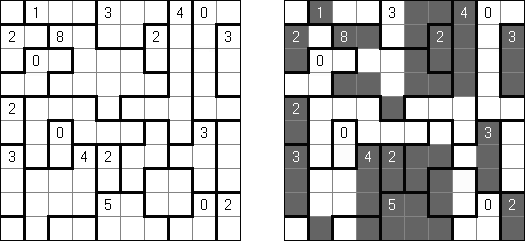
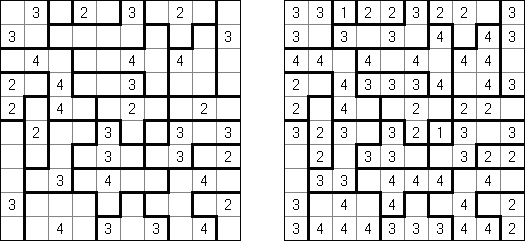
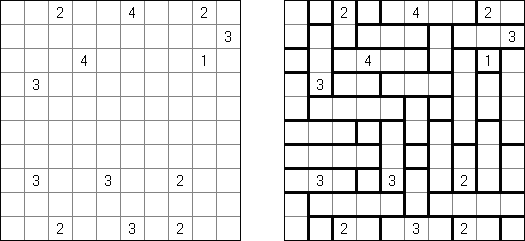
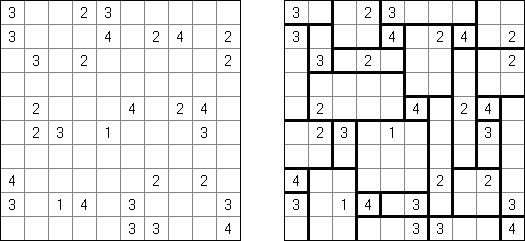
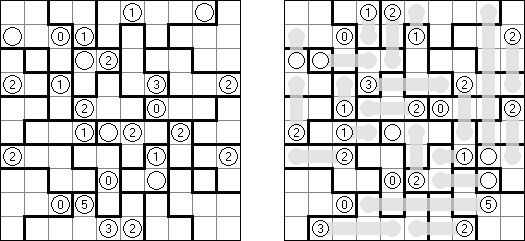
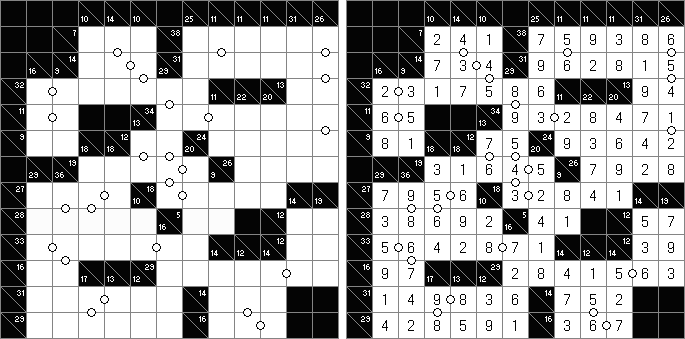
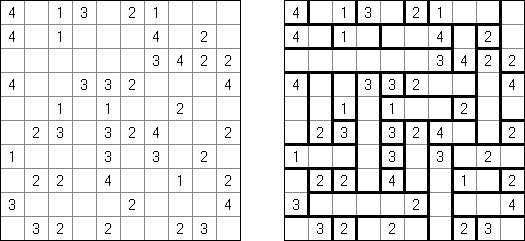
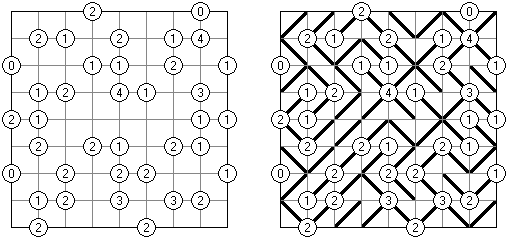
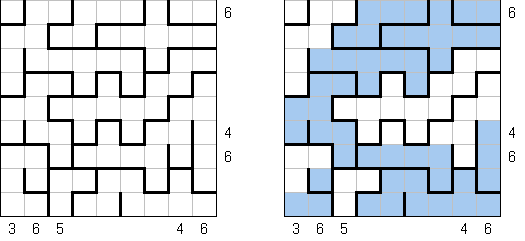
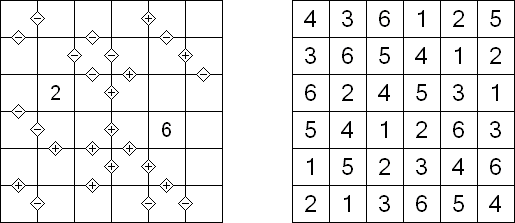
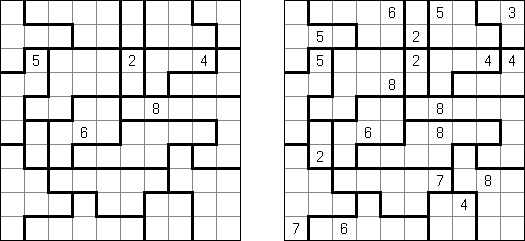
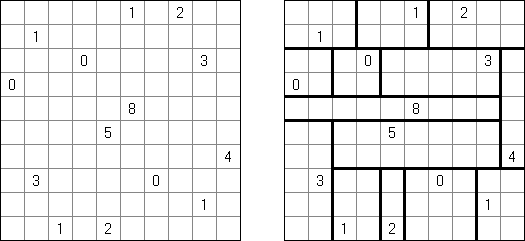
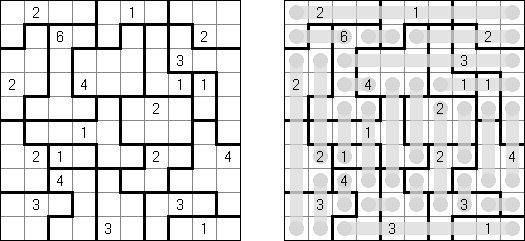
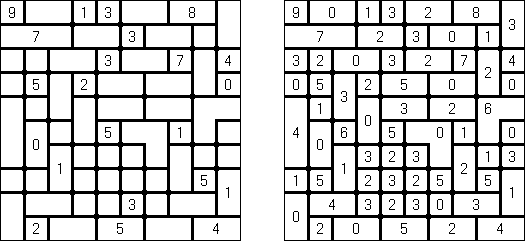
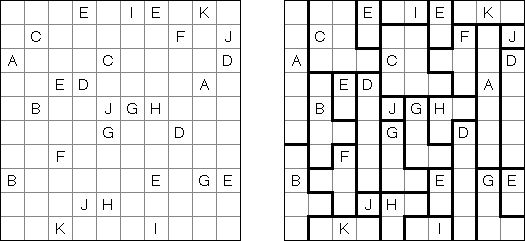
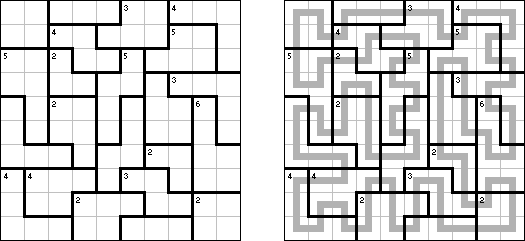
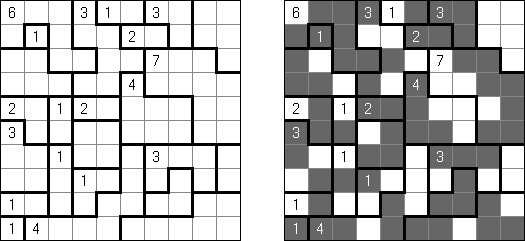
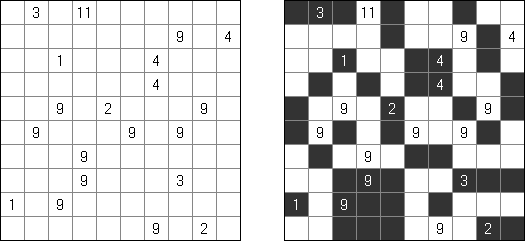
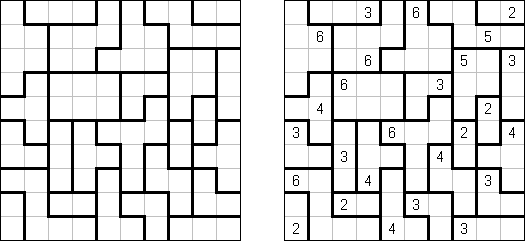
カックロ（加算クロス・サムクロス・クロスサムともいう；英語：Kakuro、Cross Sums）とは足し算のパズルで、数学クロスワードという。空マスに1～9の数字を入れる。斜めに仕切られたマスにある数字のうち、右上にある数字は横へ続く空マスの計、左下にある数字は縦へ続く空マスの計を表す。例えば、6は1+5とか4+2になる（連続する空マスに同じ数字は入らないので、3+3は書けない）。

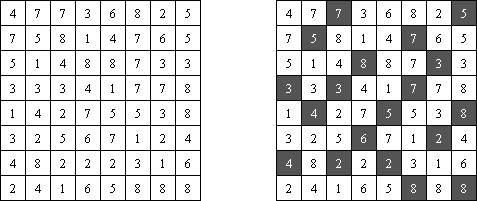
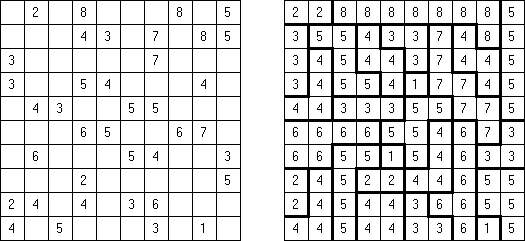
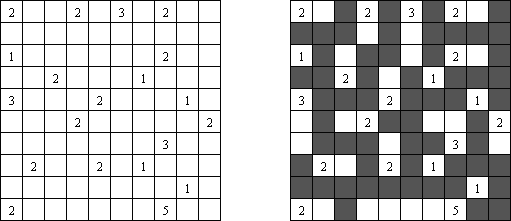
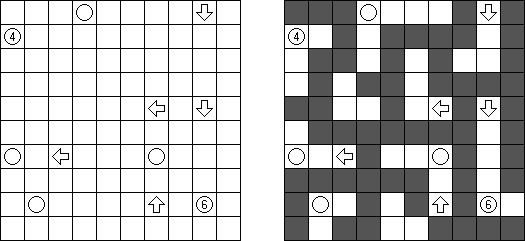
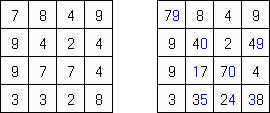
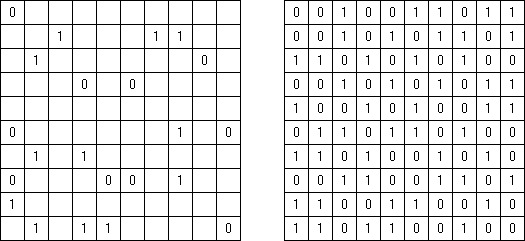
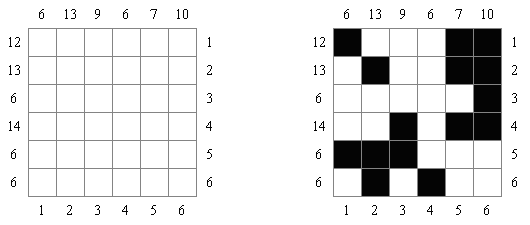
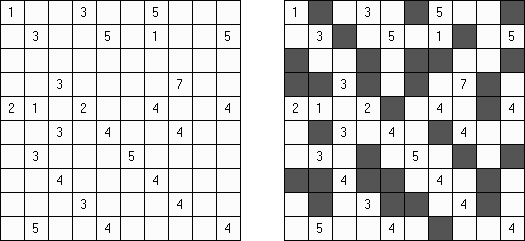
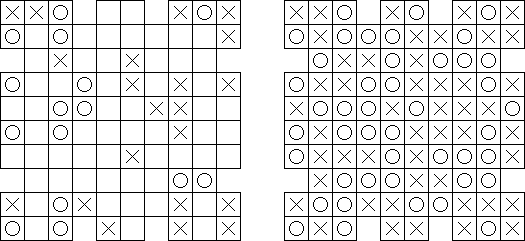
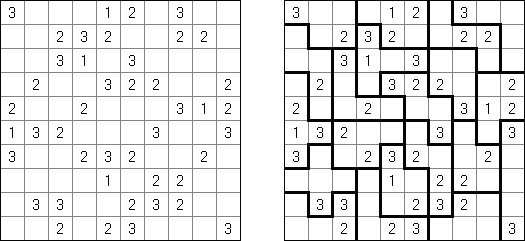
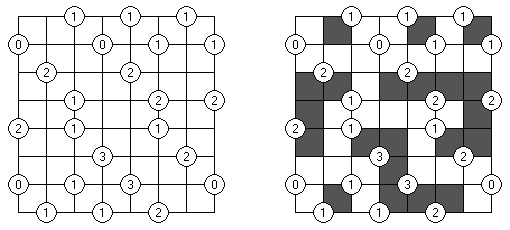
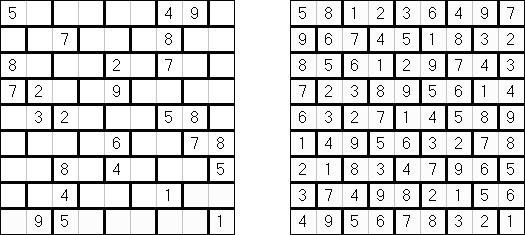
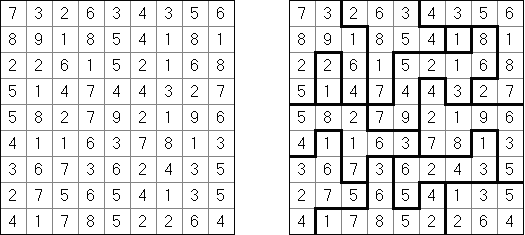
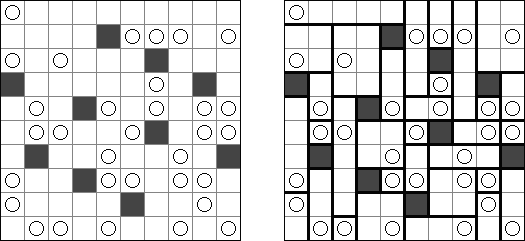
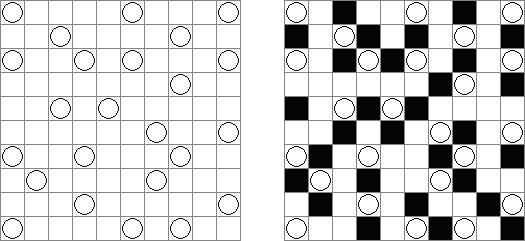
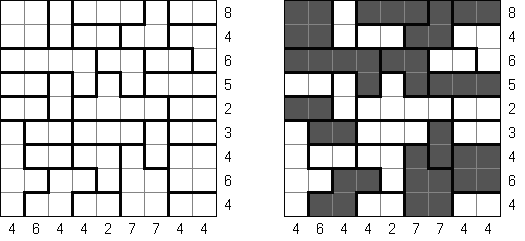
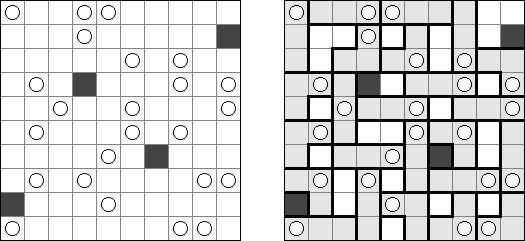
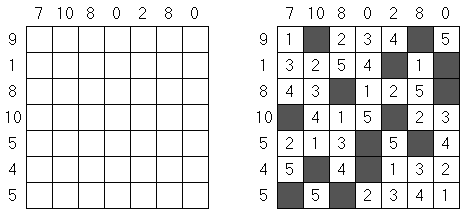
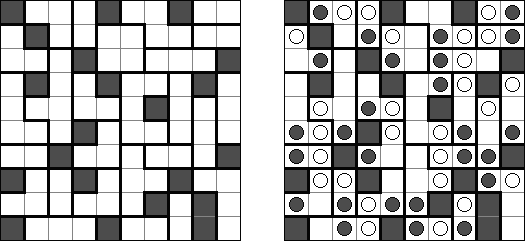
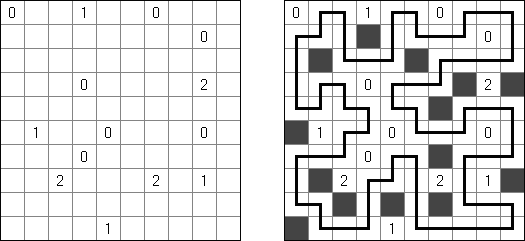
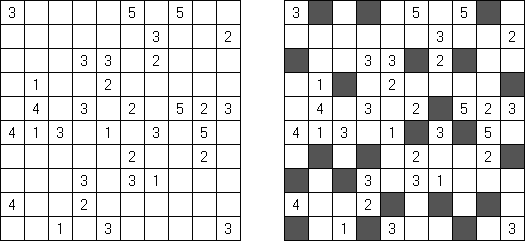
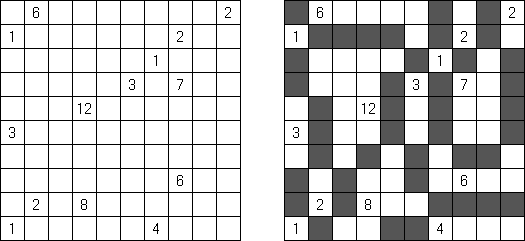
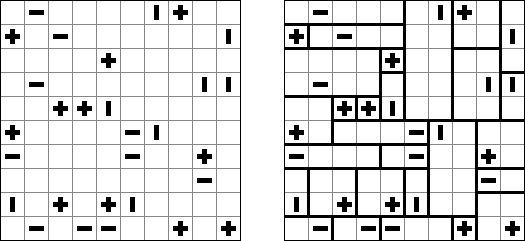
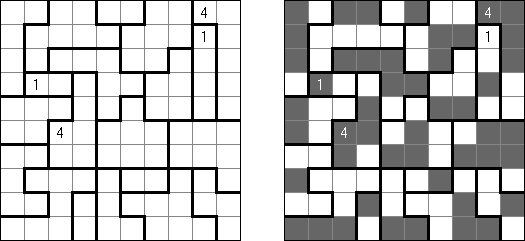
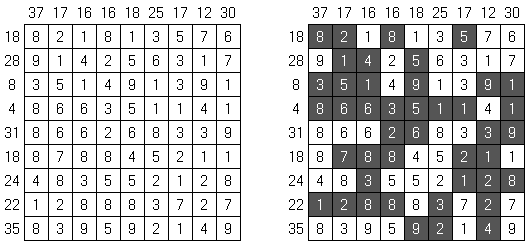
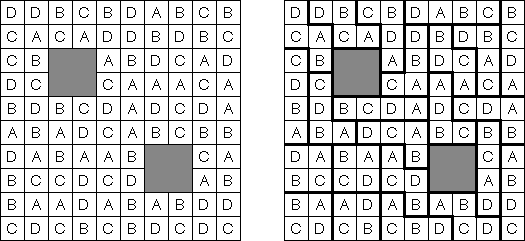
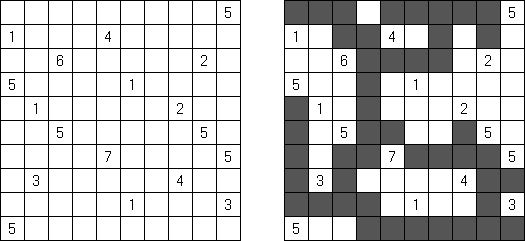
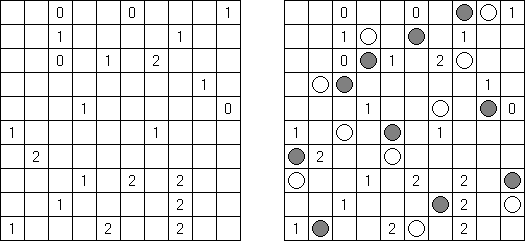
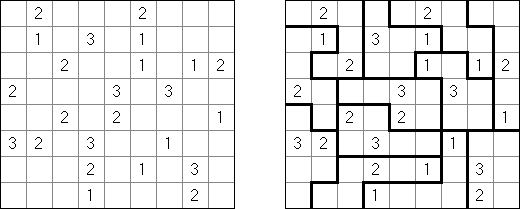
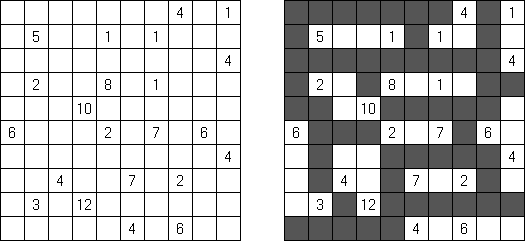
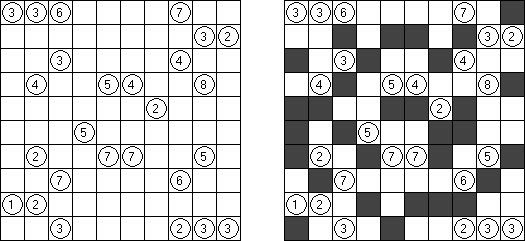
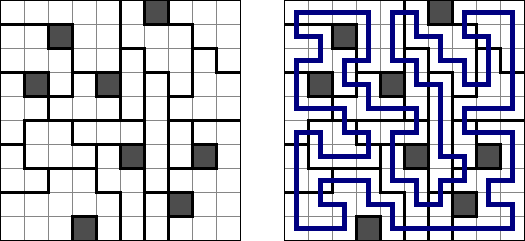
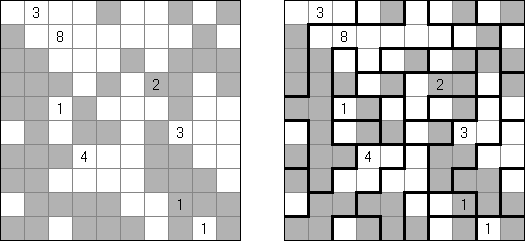
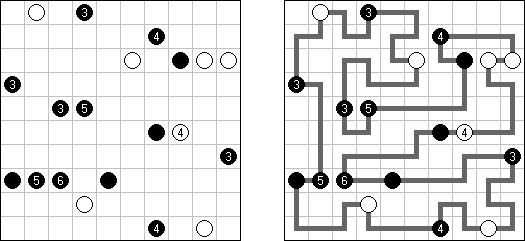
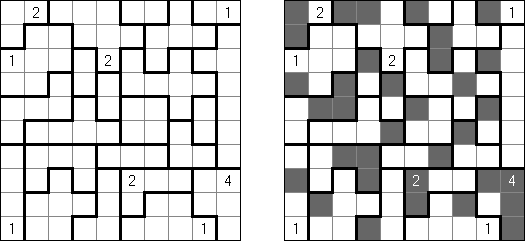
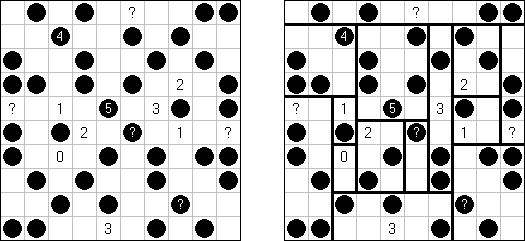
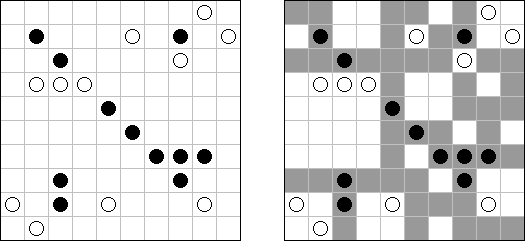
一人にしてくれ（Hitori）とは論理パズルの一つ。 各行・各列に同じ数字が残らないように、盤面に黒マスを配置する。黒マスは縦横に連続しない。また、黒マスで盤面が分断されてはいけない。

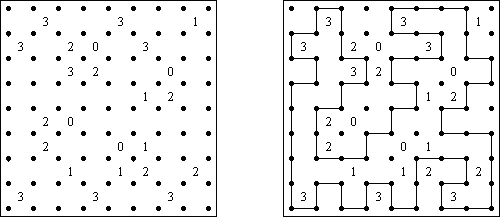
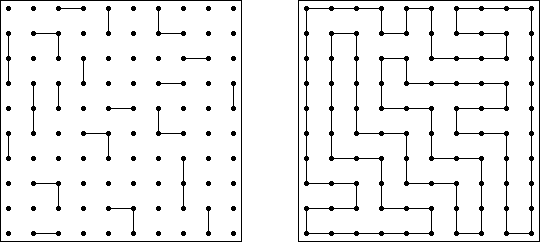
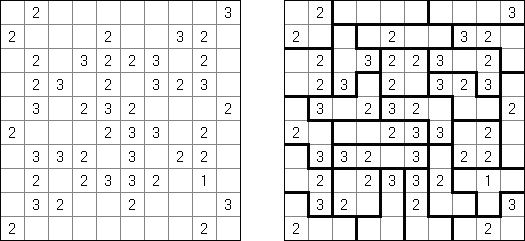
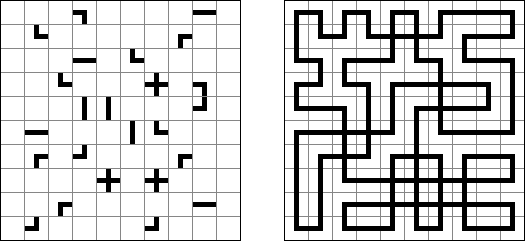
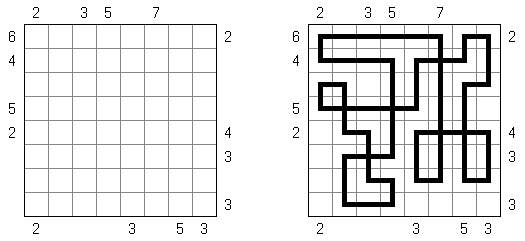
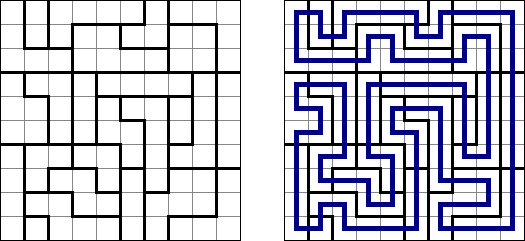
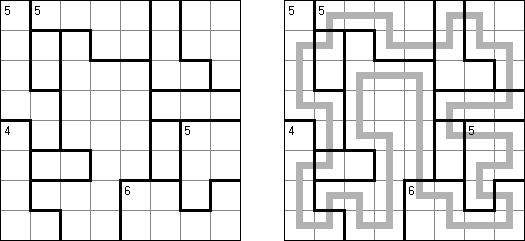
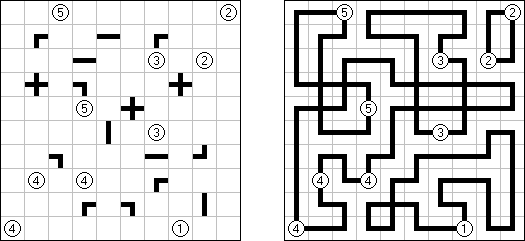
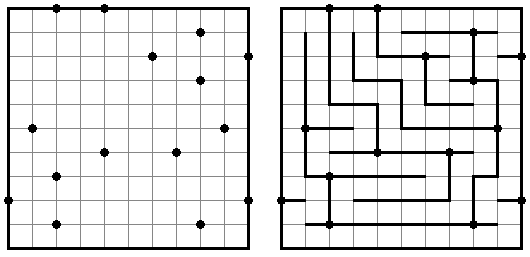
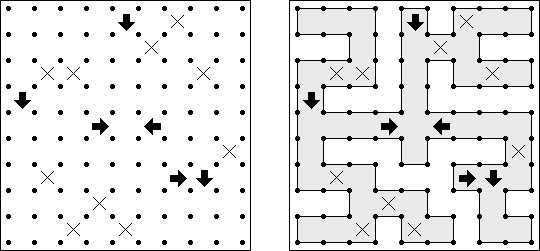
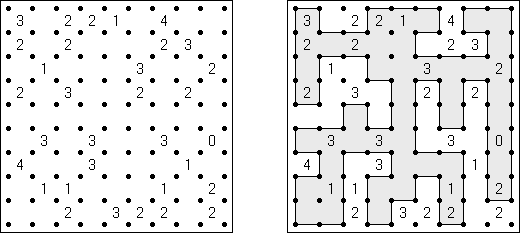
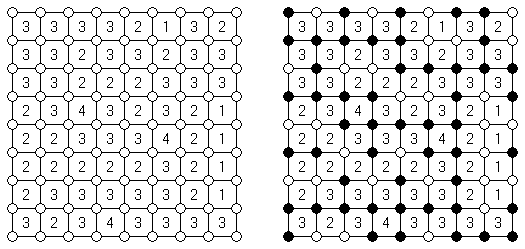
スリザーリンク（スリリンともいう；英語：Slitherlink、Fences、Loop the Loop、Dotty Dilemma、Sli-Lin）とは迷路みたいなペンシルパズルである。等間隔に碁盤の目状に配置された点の間を線分でつなぎ、盤面全体に一つの輪を作ることを目指す。点の間に書かれた数字は、その数字の周囲の4つの点の間にいくつの線分が引かれるかを示す。数字の無い所は周囲にいくつの線分が引かれるかは分からない。

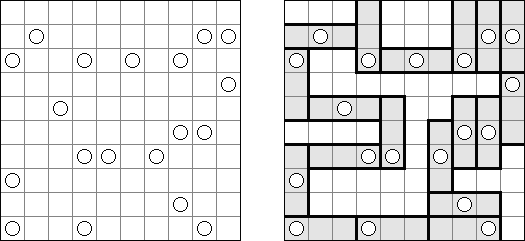
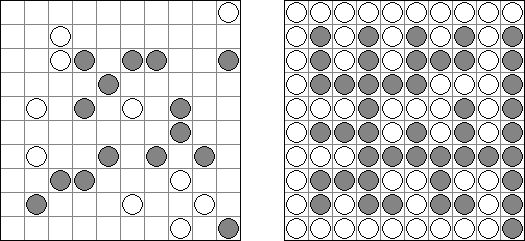
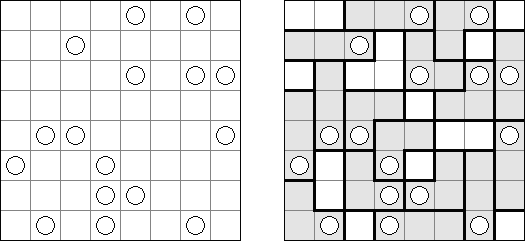
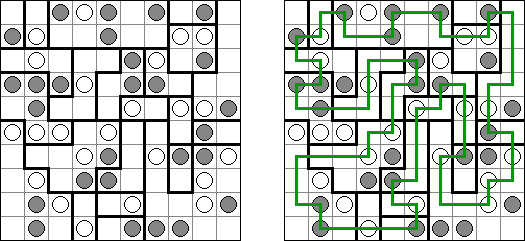
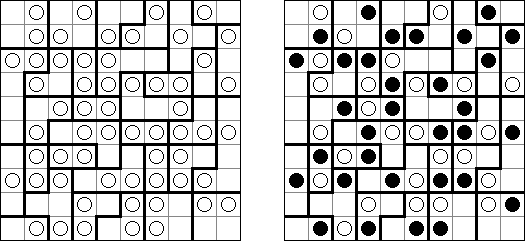
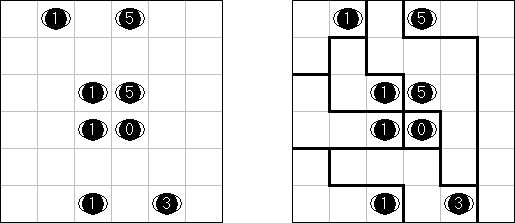
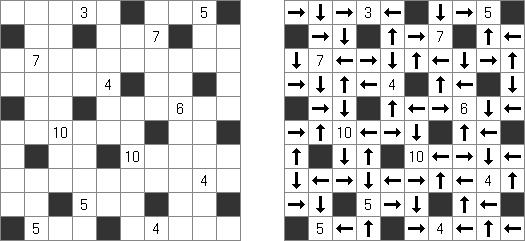
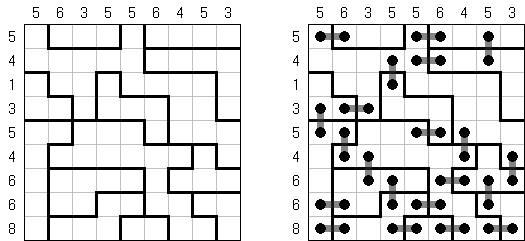
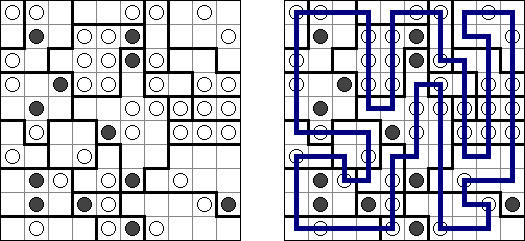
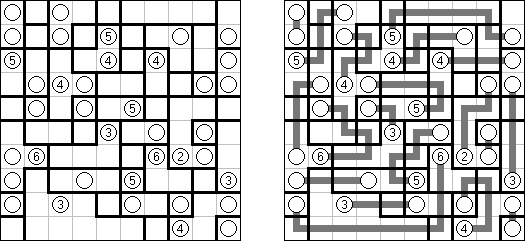
B&Wリンク絵（モノクロともいう；英語：Link-a-Pix、Paint by Pairs）とはマスを埋め、イラストを完成させるペンシルパズルである。1以外グリッドのマスに書いてある数字は全部ペアがある。1のマスはそのまま1つマスだけ塗り潰す。ペアを線でつなぐ。数字は線分の長さを表現する。数字の数だけ縦横に進み、線で結んだマスを塗り潰すと、隠れた絵が完成される。

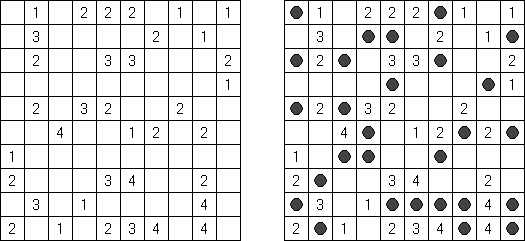
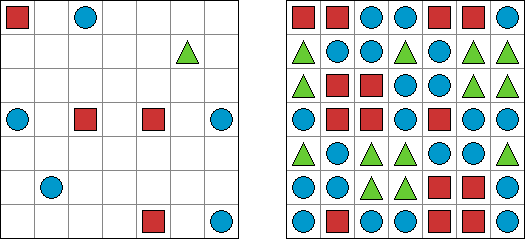
モザイクアート（Fill-a-Pix、Fill-In、Mosaic、Magipic、Nurie Puzzle、Nampre Puzzle）とはロジックをもとに盤面の数字を塗り潰すアート系パズルである。盤面にある数字をヒントに、マス目を塗り潰すかブランクにするか決定する。この数字は、数字の書いてあるマスを中心に3x3の範囲（9マス内）で塗り潰すマスの数である。例えば、0を含めた周りの9マスは全部白マスになる。

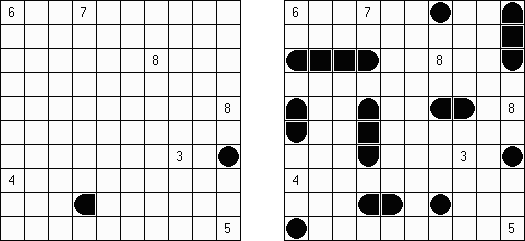
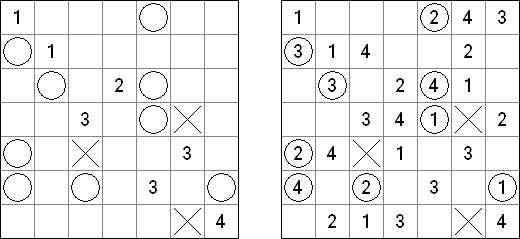
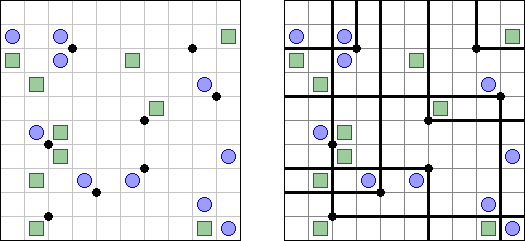
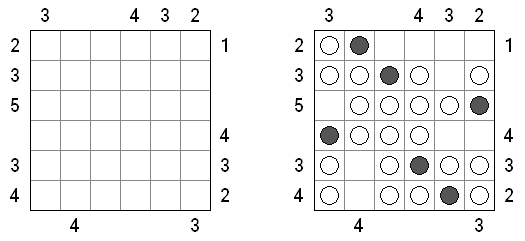
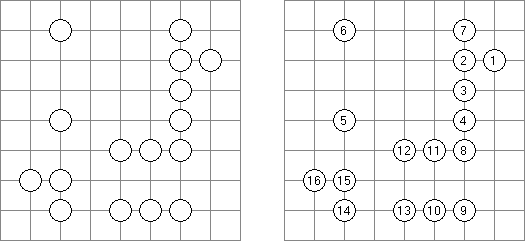
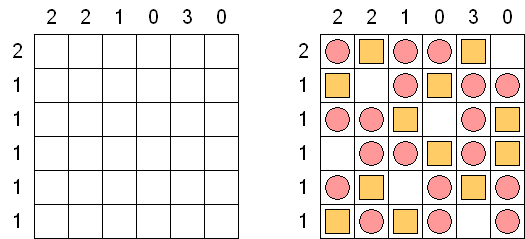
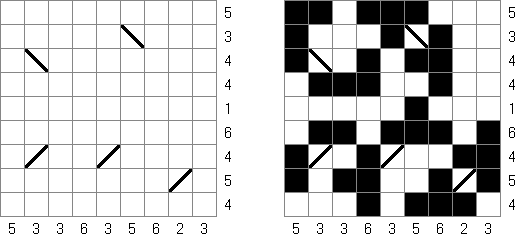
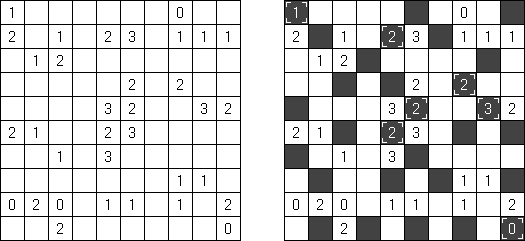
バトルシップ（Battleships、Solitaire Battleships、Battleship Solitaire）とは海戦ゲームという有名なテーブルゲームを基にしたペンシルパズルである。それぞれの船は決まった数のマスを縦または横方向に連続して占める。また、各船は互いに縦横斜めに接しない。盤面の外に置かれる数字は、その列のマスの中で艦影が存在するマスの数を表す。

一般的な10×10の枠では次のような船が用いられる：

• 戦艦（4マス分の大きさ） 1隻
• 巡洋艦（3マス分の大きさ） 2隻
• 駆逐艦（2マス分の大きさ） 3隻
• 潜水艦（1マス分の大きさ） 4隻

ゲームの始めから船の部分が指定されることもある。

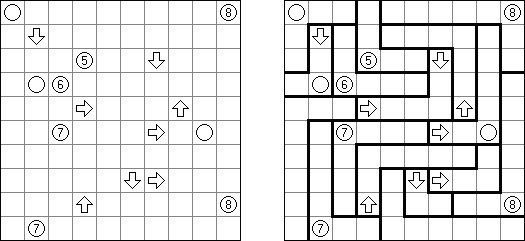
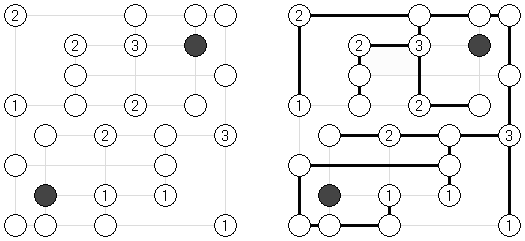
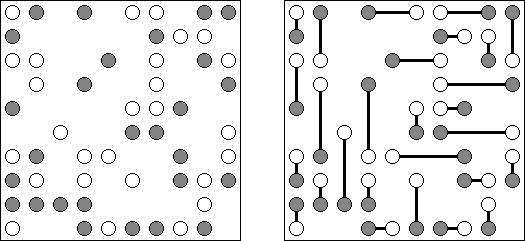
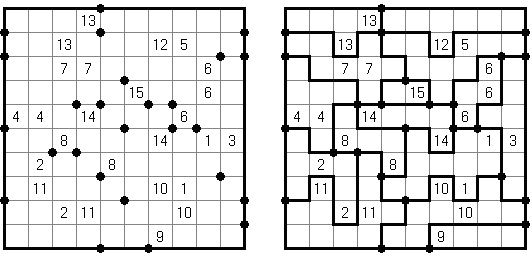
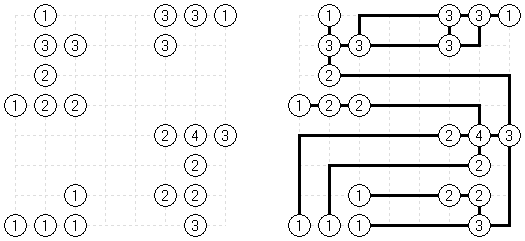
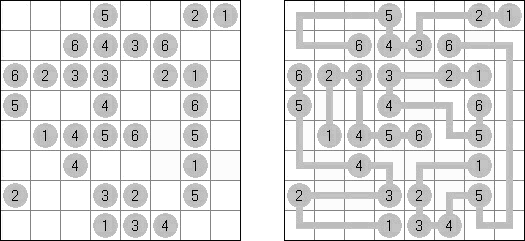
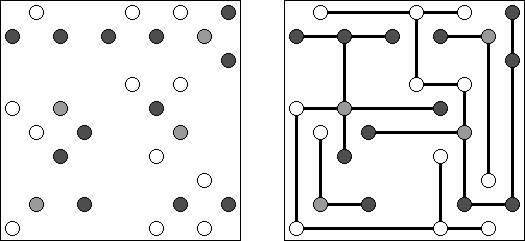
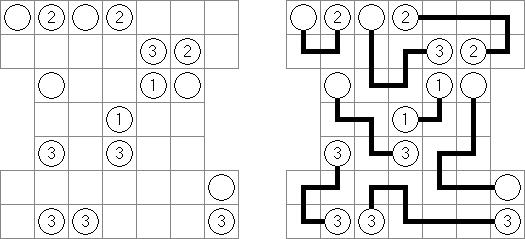
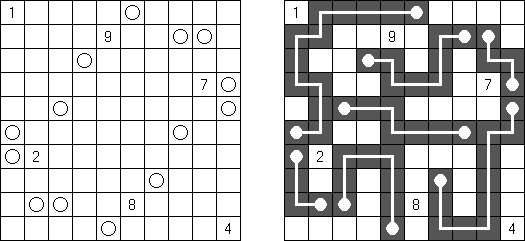
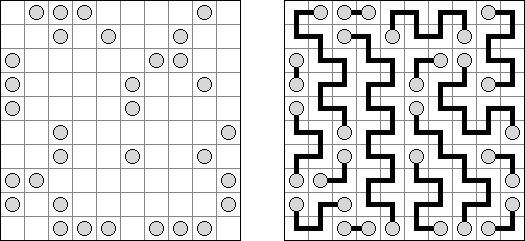
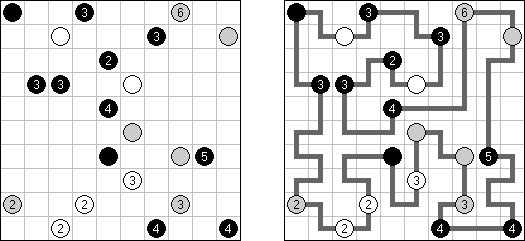
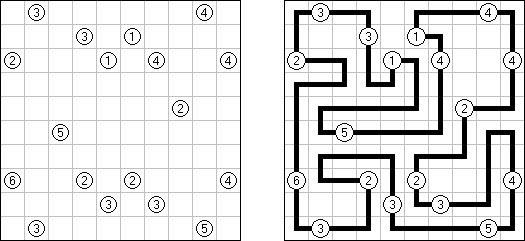
橋をかけろ（はし、ブリッジともいう；英語：Hashiwokakero、Hashi、Bridges、Chopsticks、Ai-Ki-Ai）は、数字同士を線でつなぐペンシルパズルである。丸（島同士） を線（橋）で結び、 すべての数字が線でつながっているようにする。数字はその数字から引かれる線の数を表す。どの数の間にも2本までしか線は引けない。線は縦または横方向に引かれる。線は他の線と交差したり数字を横切ったりしない。

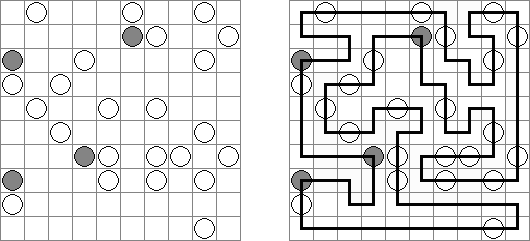
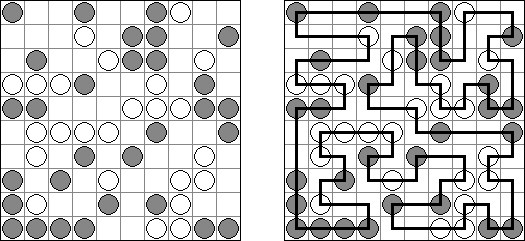
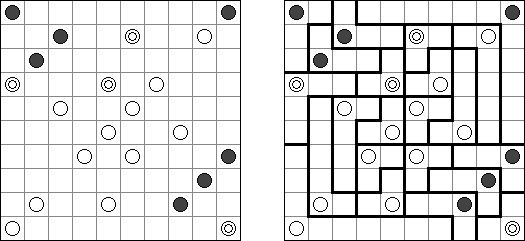
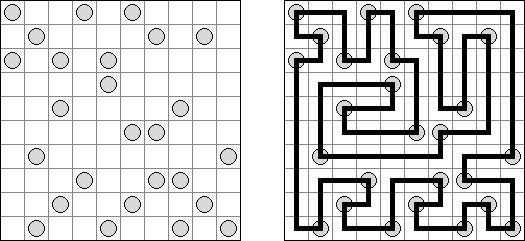
ましゅ（白真珠黒真珠ともいう；英語：Masyu、White Pearls and Black Pearls）とは白丸と黒丸を通る一つの輪を作るペンシルパズルである。1つのマスに通ることのできる線は1本だけ。白丸を通る線は、白丸のマスでは必ず直進する。両隣のマスの少なくとも1つで直角に曲がる。黒丸を通る線は、黒丸のマスで必ず直角に曲がる。黒丸の隣のマスは直進する。

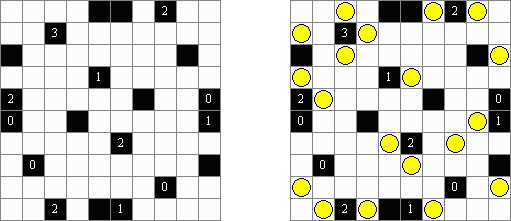
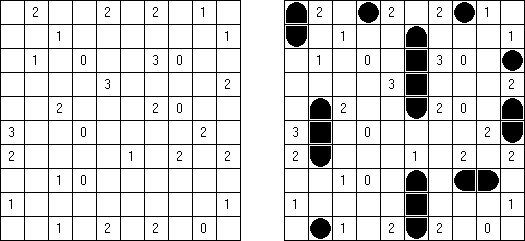
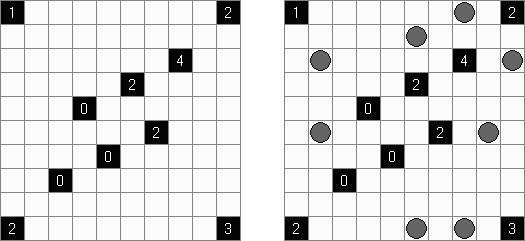
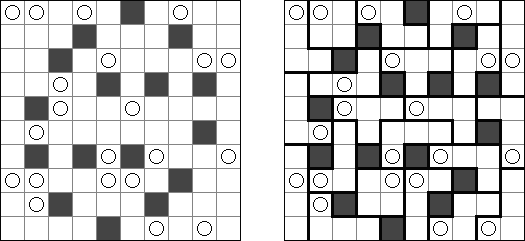
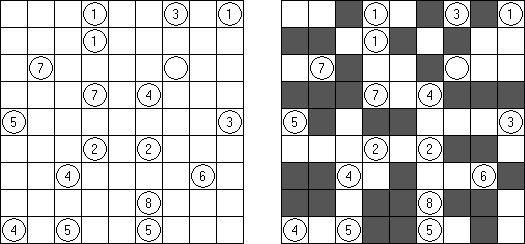
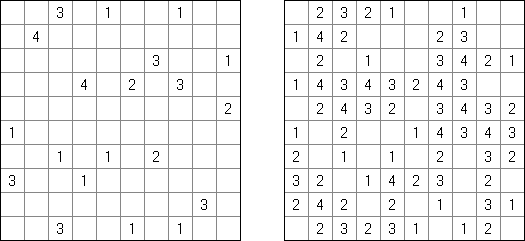
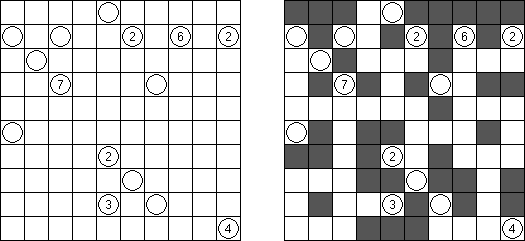
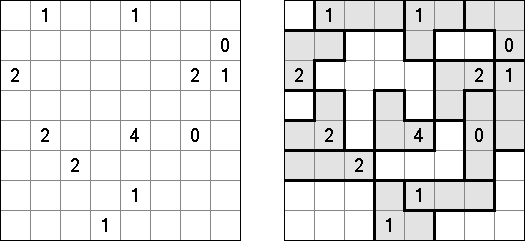
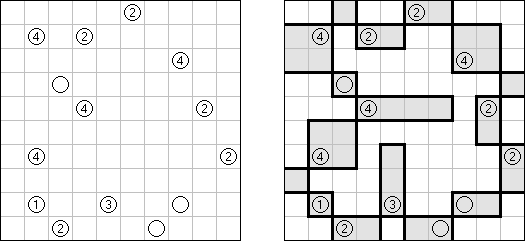
美術館（Bijutsukan、Light Up、Akari）とは論理パズルの一種である。 盤面には黒マス（この一部に数字が配置される）と白マスがある。盤面の全ての白マスの、縦方向または横方向に電球が存在するように配置するのが目的である。電球からは縦横に光が出ていて、光は黒マスでさえぎられる。黒マスの中の0～4いずれかの数字は、数字のあるマスと縦横に接する白マスにおかれた電球の数を表す。数字のないマスの周りに電球の数は限られていない。しかし、電球がおかれたマスには、他の電球からの光が当たってはいけない。

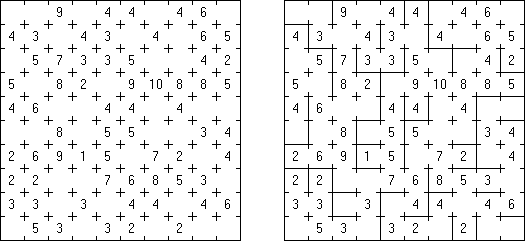
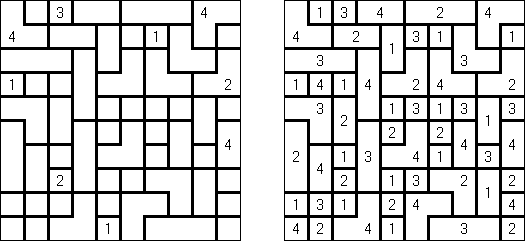
フォルイミノ（Fillomino、Polyominous）とは盤面を数字で埋めるペンシルパズルである。 ヒント数字をもとにし、盤面を複数のブロックに分割することを目的とする。マスの中の数字はブロックの面積を表す。パズルを解くように、空マスに数字を入れ、ブロックの部分とする。つながった同じ数字は、別の同じ数字のつながったものと辺を共有しない。

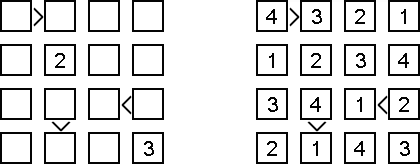
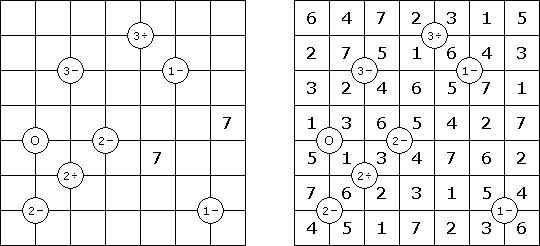
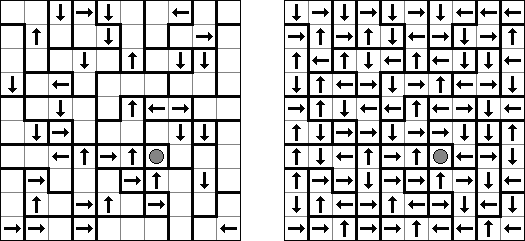
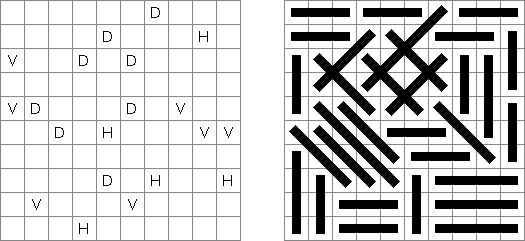
不等式（不等号ナンプレともいう；英語：Futoshiki、Hutoshiki、Unequal）とは数独に似ている論理パズルである。盤面のマスにはいくつかの数字、マスの間に不等号がある。不等号に矛盾がないように、また、縦と横の列で同じ数字が重ならないように、全ての空マスを数字で埋めることはゲームの目的である。

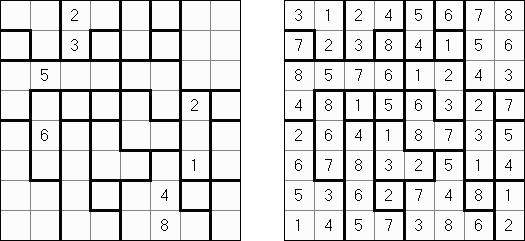
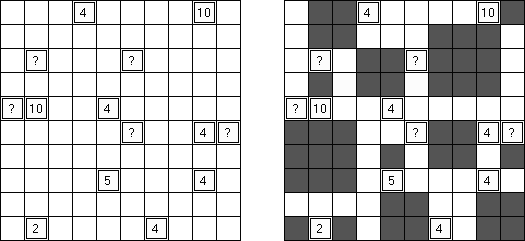
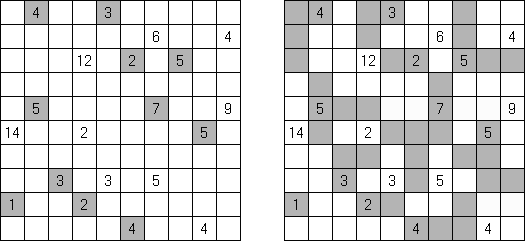
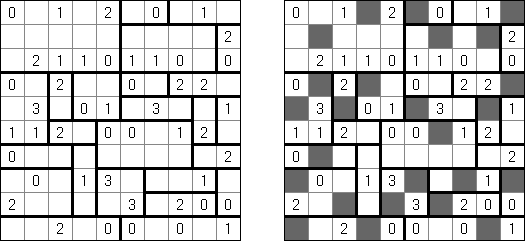
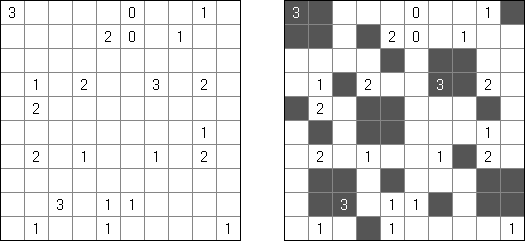
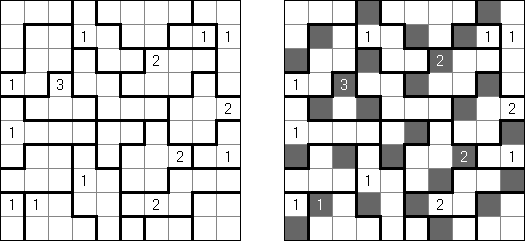
黒どこ（黒マスはどこだ；英語：Kuromasu、Kurodoko、Where is Black Cells?）とはグリッドに黒マスを配置するペンシルパズルである。ヒント数字をもとにし、次のようなルールに従い、マスを塗り潰す：

• 数字は、その数字から上下左右の各方向に連続していくつの白マスがあるかの合計を示す。
• 数字があるマスは常に白マスになる。
• 黒マスは縦横に連続しない。
• 黒マスによって盤面が分断されてはいけない。

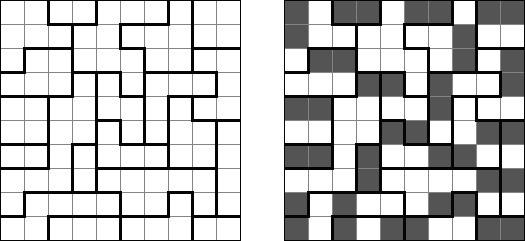
ぬりかべ（部屋の構築、島と潮流、煉瓦を敷くともいう；英語：Nurikabe、Cell Structure、Islands in the Stream）とは数字を使うペンシルパズルの一種である。日本の民話に塗壁というのは夜道で人間の歩行を阻む、姿の見えない壁のような妖怪という意味があった。

ゲームの目的は、ルールに従い、問題に記された数値と等しい面積のブロック（「島」）に分割されるように黒マス（「川」）を配置していくことである。

• 数字は「川」に囲まれた白マスの「島」の面積であり、各「島」には数字が一つだけ入る。
• 「島」は縦横に連続しない。
• 全ての黒マスは縦横に一つつながりになる。
• 黒マスが2×2以上の固まりになってはいけない。

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

ヤジかべ（Yajikabe） was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

テントサイト（テントともいう；英語：Tents、Tents and Trees）とは理論ペンシルパズル一種である。マスには「木」があり、次のようなルールに従い、「木」の隣に"テント"を配置するようにする：

• 全ての「木」に一つずつ"テント」をつなげる。
• 「テント」は、つなげる「木」の隣のマスに置くようにする。
• 「テント」は縦横斜めで接しない。
• 盤外の数字は、その列に入る「テント」の数を表す。

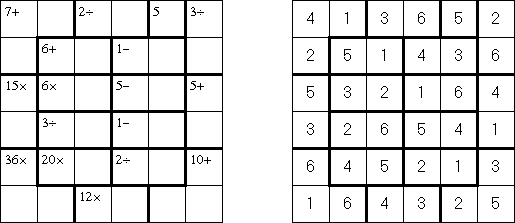
堅くなるパズル（Calcudoku、KenKen、KENKEN、KenDoku、Square Wisdom）とは数学的な論理パズルである。枠内の縦横同じ数字が重複しないよう一つずつ入れる。予め記された数字と加減乗除の記号は、太線で区切られた空間内に入る数字の全てを加減乗除した結果を示している。キラー数独と違って、ブロックの中に同じ数字を置いてもいい。

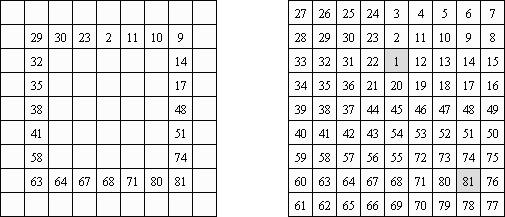
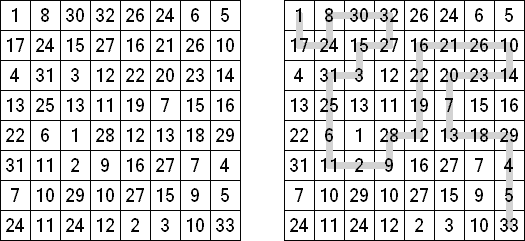
ヒダド（イディッシュ語で「私のパズル」;英語：Hidato、Hidoku）とはギオル・ベネディック（Gyora Benedek）というイシラエルの数学者に作成されたパズルである。 1から順番に数字を縦、横、斜めのいずれかにつなげていくようにする。パズルには最大と最小の数字が予め記される。ゲームを簡単にするとか、一つだけ正解があるように、外の数字も記されることが多い。

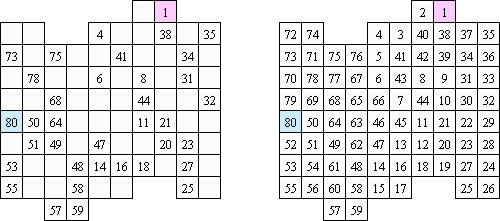
ナムブリックス（Numbrix）とは1から81までの数字を並べるパンシルパズルである。9x9のマスにヒント数字があり、これをもとにし、1から81までの数字を縦横に順番に並べるようにする。斜めに並べてはいけない。

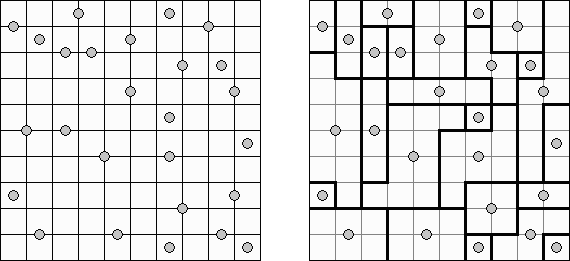
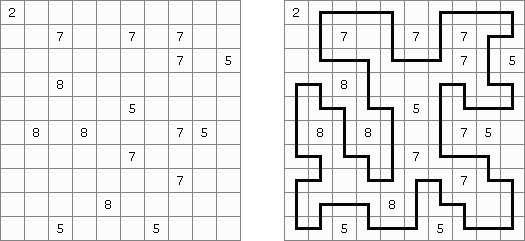
四角に切れ（ナンバーエリアともいう；英語：Shikaku、Divide by Squares、Divide by Box、Number Area）とはペンシルパズルの一種である。配置された数字をもとに盤面を長方形に分割する。各長方形は数字を1つずつ含む。この数字は長方形の面積を表す。

天体ショー（Galaxies、Tentai Show）とは論理と幾何学を兼ね備えるペンシルパズルである。 丸を含む正方形のグリッドを分割する。各ブロックには丸は一つだけあり、全てのブロックは丸を中心に点対称の図形になる。

スカイースクレーパー（Skyscrapers）とはビルディングパズルの一種である。縦横の全ての列に、指定された範囲の数字を一つずつ入れる。縦横の列で同じ数字が重ならないようにする。それらの数字は、そこに配置されている「ビルの階数」を表す。盤外の数は、その方向から見たとき、最初の「盤面の端」までにいくつのビルが見えると表す。

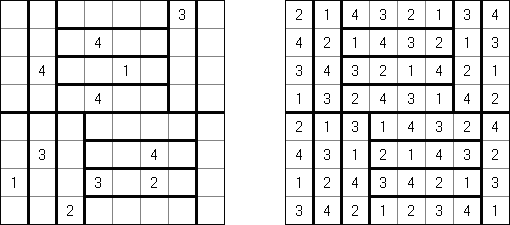
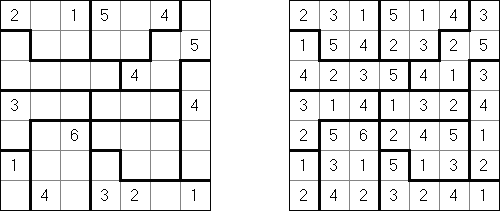
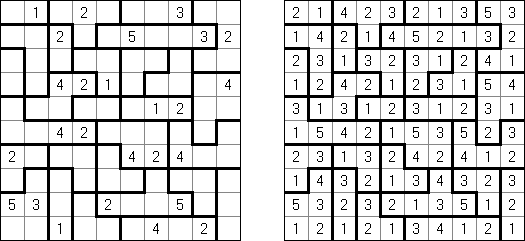
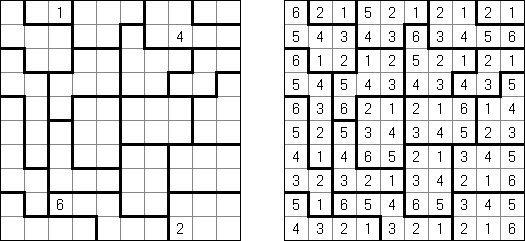
波及効果（Hakyuu、Hakyuu Kouka、Hakyukoka、Ripple Effect、Seismic）とは理論パズルの一種である。 太線に区切られたブロック（「部屋」）の全てのマスに、1からその「部屋」のマス数までの数字を1ずつ入れる。同じ数字を、縦横の同じ列に入れる場合は、数字と数字の間に、数字と同じ数以上の他の数字がなければいけない。例えば、5を二つ同列に入れる場合は、その間に5マス以上他の数字を配置しなければならない。

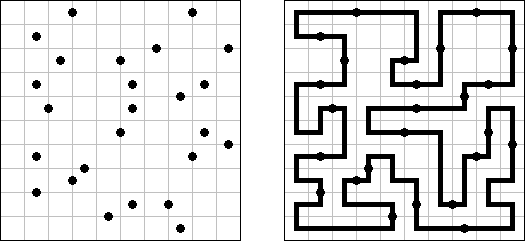
グランド・ツア（Grand Tour）とは正方形のグリッドの全ての点を通り、交差や枝分かれはしない一つの輪を作ることを目指す論理パズルである。正しい答えが一つだけあるように、一部のセグメントは予め記される。

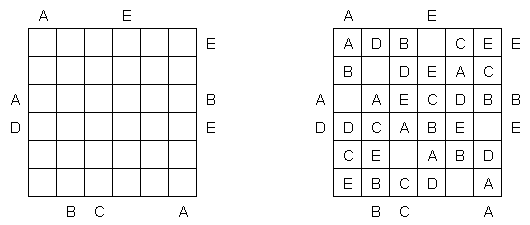
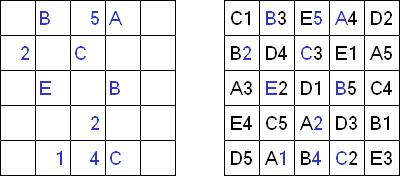
ABCプレース（Easy as ABC、ABC End View、Last Man Standing）とは文字を使う論理パズルである。縦横の各列内に、指定された範囲のアルファベット（例えば、A-E）1個ずつ入るようにする。 文字が入らないマスもある。枠外のアルファベットは、その列で最も辺に近い位置にあるアルファベットを表す。

クラウドズ（雲；英語：Clouds、Rain Clouds、Radar）とはバトルシップいうパズルの一種である。縦横斜めに互いに接しないように長方形の「雲」を盤面に配置する。盤面の外に置かれる数字は、その列に「雲」が存在するマスの数を表す。「雲」の数とサイズは指定されないが、長方形の辺は2マス以上である。

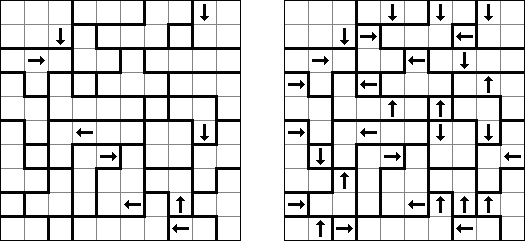
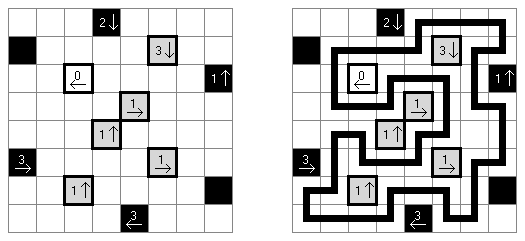
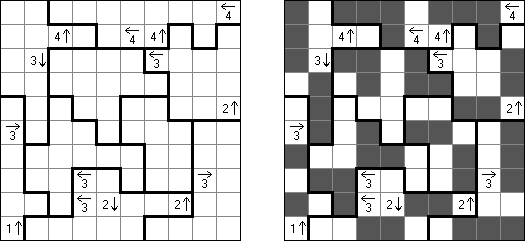
ヤジリン（Yajilin、Arrow Ring、Straight and Arrow）とは長方形か正方形の論理パズルである。目的は、盤面に黒マスを配置しつつ輪を完成させることである。記された数字は、黒マスを正しく置くために必要である。 The grid may contain gray cells that can not be part of the loop.

• 数字は、同じマスに入っている矢印の方向に入る黒マスの数を表す。このマスは黒マスとして扱わない。
• 線は縦横のマスの中央を通り、1マスに1本だけ通過できる。線は交差や枝分かれはしない。
• 数字は入っているマスと黒マスの外の全てのマスに線が通る。
• 黒マス同士は隣り合わない。
• 盤面に矢印に示されていない黒マスもある。

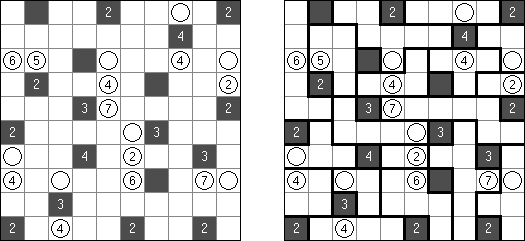
マインスイーパ（Minesweeper）は Microsoft Windows を使う人が皆知っているパズルである。 ヒント数字を使い、地雷（マイン）を配置することが目的である。各数字は、隣接するマスでの地雷の数を表す。各マスに地雷が一つ、数字のマスに地雷がない。

マインスイーパ・バトルシップ（Minesweeper Battleships、Battlemines）は人気なパズルの2つの種類を結合する。各船は互いに縦・横・斜めに接しない。マスの一部には数字がある。数字はまわりのマスに（斜めのマスも含んで）存在するバトルシップの部分の合計を表す。

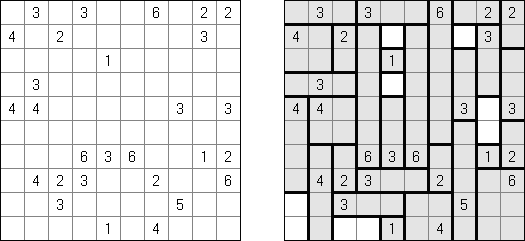
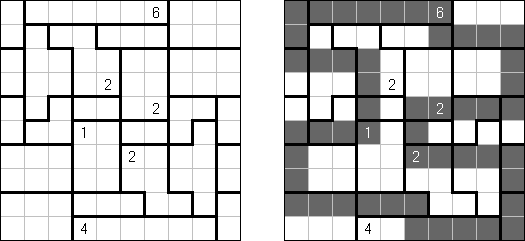
へやわけ（Heyawake）とは黒マスを塗り潰すペンシルパズルの一つである。長方形のグリッドは「部屋」に太線で区切られる。出ている数字は、「部屋」の中に入る黒マスの数を表す。 数字が入っていない「部屋」にいくつの黒マスが入るか分からない。

• 黒マスは辺で接しない。
• 黒マスにより盤面が分断されることがない。
• 白マスは縦横にまっすぐに3つの「部屋」にわたって続けてはいけない。

テンナー・グリッド（Tenner Grid、From 1 to 10、Zehnergitter、Grid Ten）は10マスの広さがある長方形のグリッドを使うペンシルパズルである。各横列に0～9を入れる。縦列に同じ数字があってもいい。グリッドの下の数字は縦列の数字の合計を表す。縦横斜めに連続するマスに同じ数字を入れてはいけない。

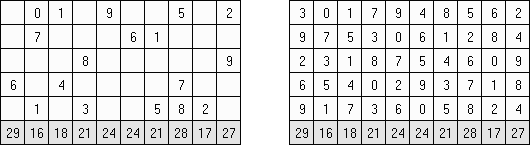
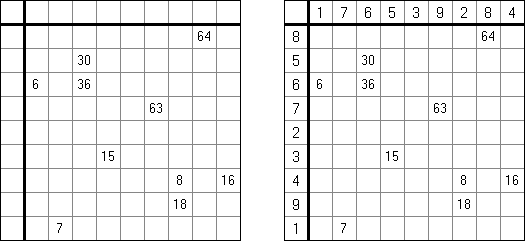
ハンドレッド（百；英語：Hundred）というパズルの正方形の盤面にヒント数字がある。各縦列や各横列の合計は100になるように、数字を入れることがゲームの目的である。

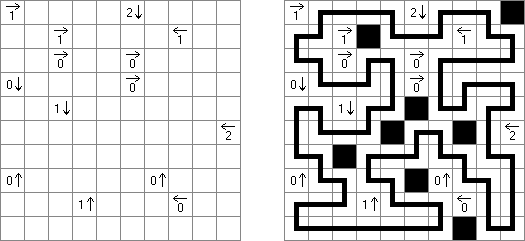
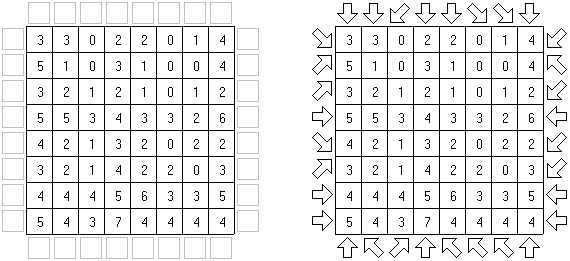
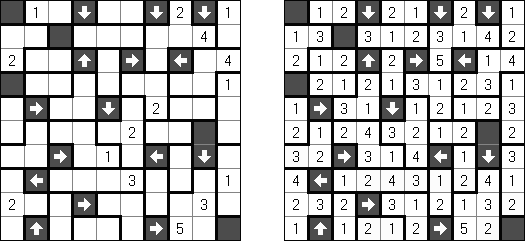
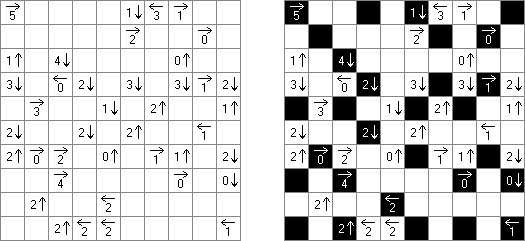
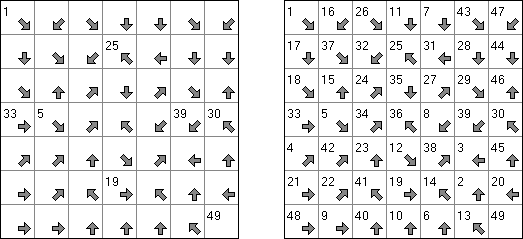
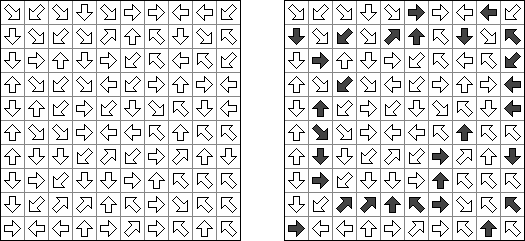
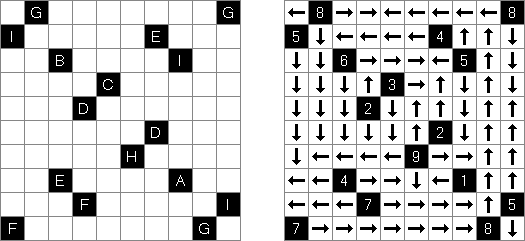
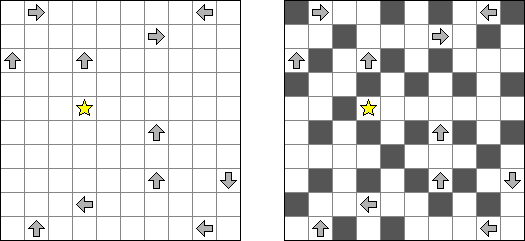
アローズ（矢印；英語：Arrows）は論理パズル一種である。長方形のグリッドの各マスに数字がある。ゲームの目的は盤面の外に矢印を配置することである。各矢印は少なくとも一つのマスの方向を指す。数字はマスの方向を指す矢印の数を表す。

メトレックス（Mathrax）とは論理パズルの一種である。盤面の縦列や横列に同じ数字は重ならないように、マスに数字を入れることは目的である。一部の数字は予め問題に記されている。グリッドの線の交差に、次のような追加の条件を含む丸もある：

• 数字や加減乗除の記号：丸の中の数字は加減乗除した結果を示す。加減乗除のため丸に隣接する互いに斜めにある数字のペアを使う。
• 丸の中にEの文字があれば、丸を囲むマスに全ての数字は偶数である（「E」は英語の「even」の省略）。
• 丸の中にOの文字があれば、丸を囲むマスに数字は全て奇数である（「O」は英語の「odd」の省略）。

ストレイトス（Str8ts または Straights とはポーカーの用語：順番にした5枚のトランクの意味）とはカナダアのジャッフ・ヴィッデリチ（Jeff Widderich）に作成された論理パズルである。正方形のグリッドに白マスと黒マスがあり、白マスを数字で埋めるのがゲームの目的である。必ずしも数値は順序で指定する必要がないが、連続番号を記入する必要がある（例えば、2-1-3-4）。 縦横列に同じ数字を埋めてはいけない。 黒マスの数字は白マスの連続した数字群に入らない。

ラインスイパー（Linesweeper）とはマインスイパーに似ているルールに従うパズルである。長方形のグリッドに0～8の数字が入る。ゲームの目的は、空マスを通る輪を完成することである。輪の線は、交差や枝分かれはしない。数字は、線に通られるマスの数を表す。

バイナリ・パズル（Binairo、Binary Puzzle、Takuzu、Tohu wa Vohu）とは「0」と「1」を使用する論理パズルである。次のようなルールに従い、長方形のグリッドを数字で埋めるのは目的である：

• 各縦列と各横列に「0」と「1」の数は同じである。
• 同じ数字を連続する2つのマスだけに入れるようにする。
• 各縦列と各横列はユニークである。

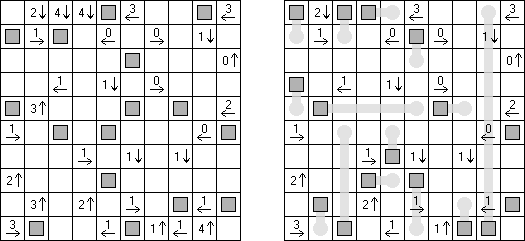
ウォールズ（Walls）とは日本人の稲葉直貴に制作された論理パズルである。全ての白マスに縦棒か横棒のいずれかを入れる。目的は、黒マスの数字と黒マスから出る「光」の長さの総和を同じすることである。

ドミノサ（Dominosa、Dominosa Omnibus、Solitaire Dominoes、Domino Hunt）とはドミノ牌を利用する論理パズルである。盤面には数字だけあり、ゲームの目的はドミノ牌の間の「境」をかくことである。

パッチワークまたは畳（Patchwork、Tohu wa Vohu、Tohuwabohu、Tatami）は正方形のグリッドを「部屋」というエリアに分けることを目的とするパズルである。各部屋に1からエリアのマスの合計を表す数字までの数字を書く。各横列・縦列に各数字の数は同じである。同じ数字のマスは縦横に連続しない。

このパズルには数字の代わりに文字を使うこともある。Cross+Aは数字のタイプも文字のタイプも解決できる。

クノッソス（Knossos；クノッソスとはギリシャのクリタ島の昔の都市や宮殿の名前。そして、ミノタウロスが閉じ込められていたラビリンスの場所）は数字が入っている四角のグリッドを利用するゲームである。数字がエリアのマスの合計を表すように、グリッドを「部屋」に分けることはゲームの目的である。

レクトサイズ（Rekuto）は四角のパズルである。マスの一部に数字が入っている。目的は数字が1つずつが入るようにパズル面を長方形に分割することである。数字はその数字を含むエリアの縦と横の長さの総和を表す。

隣（Neighbours）は自由な形のグリッドを利用するパズルである。あるマスには数字あるいは疑問符が入っている。目的は数字あるいは疑問符が1つずつが入るようにパズル面をエリアに分割することである。数字はエリアの「隣」の個数を表す。そのエリアが辺で接している他のエリアを「隣」と呼ぶ。疑問符のエリアの「隣」の数は自由である。

4つの風（Four Winds、Line Game）は白マスと黒マスからなっている四角のグリッドを利用するパズルである。目的は、黒マスの数字と黒マスから出る「光」の長さの総和を同じすることである。線は交差しない。

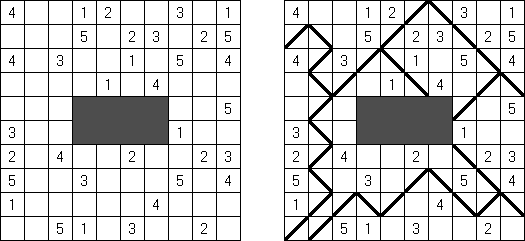
シャカシャカ（Shakashaka、Proof of Quilt）は四角の論理パズルである。黒マスと白マスがあり、黒マスの一部に0～4の数字が入っている。白い四角のエリアを作るように白マスに黒い三角を入れる。ある白マスは空のままに残る。エリアは横・縦・斜めになる。隣の白いエリアは辺で接していない。黒マスの数字はこのマスと隣接する黒い三角の合計を表す。

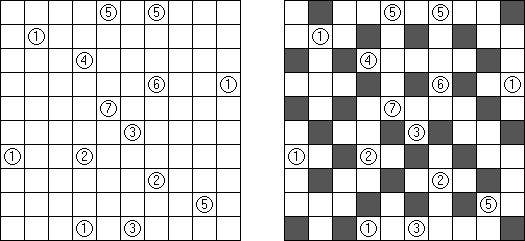
カクラス（Kakurasu、Index Sums）とは、白マスと黒マスを配置することを目的とする長方形のパズルである。盤の左と上にある数字は、縦・横列の黒マスの「重量」の和を示す。盤の右と下にある数字は、それらの縦・横列の黒マスの「重量」を示す。（第１縦・横列の黒マスの「重」は１で、第２縦・横列の黒マスの「重量」は２になり、などである。）

モチコロまたはモチヌリ（Mochikoro、Mochinuri）は長方形のパズルの一つである。マスの一部には数字が入っている。 白マスのエチアをいくつか作るようにマスを塗る。

• 白いエリアには数字が一つだけ入っている。 数字は、そのマスを含むエリアの面積を表す。
• 数字が入らないエリアもある。
• 白いエリアは辺を共有しないが,すべての白いエリアは角がつながる。
• 黒マスは2×2マス以上のカタマリになってはいけない。

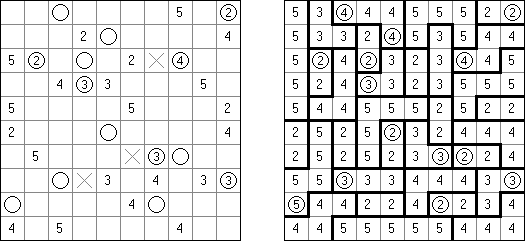
ドア（Seethrough、Doors、Open Office）とは、各マスは「部屋」を示す長方形の論理パズルである。部屋の間の「ドア」を開けたり、閉めたりしなければならない。ドアが開いているなら、外の部屋をいくつか「見る」ことができる。数字は、その部屋から縦・横に見たときに「見える」部屋の数を表している。数字のある部屋自身はカウントに含めない。ドアによって盤面が分断されてはいけない。

灯台（Lighthouses）とは、数字が入る「灯台」という黒マスが配置される論理パズルである。灯台に書かれた数字は、この灯台に照らされる船の数を表している。灯台が照らす範囲は、その灯台と同じ縦・横列にあるすべてのマス。間に外の灯台か船があっても、灯台は同じ列の船を照らす。どの船も、少なくとも１つの灯台に照らされていなければならない。船は互いに縦・横・斜めに接してはいけない。また、灯台に縦・横・斜めに接するマスにも船を配置する異はできない。

ライトハウス・バトルシップス(Lighthouse Battleships)は「ライトハウス」、「バトルシップス」というパズルの組み合わせである。四角形や長方形の網は、数字が入っている枠(灯台)がある。その数字は灯台と同じ横、縦列にある船の部分の数を意味する。数字の枠は船の部分にならない。船は他の船、灯台に繋がられない。

タパ（Tapa）はトルク人のセルカン・ユレクリ（Serkan Yurekli）によって考案されたパズルである。そのパズルは白マスの長方形のグリッドがある。以下のルールを満たすように、盤面のマスを塗りつぶす：

• マスの中の数字は、そのマスの周囲の最大8マスを順に見たときに、黒マスが連続している長さを表す。複数の数字がある場合は、それぞれが白マスで分かれていることを表す。
• 数字か疑問符の入っているマスは、黒マスにならない。
• 黒マスは縦・横にひとつながりになる。
• 黒マスが２×２のカタマリになってはいけない。
• 疑問符は0以上の数字を表す。

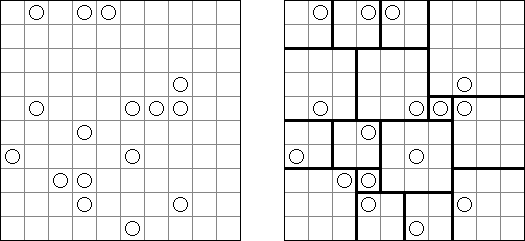
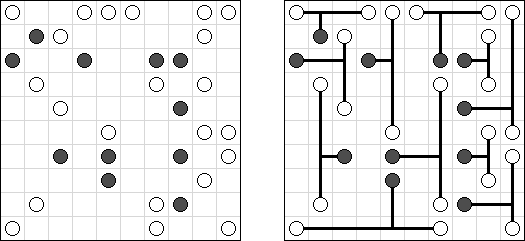
フォービドゥン４ （Fobidoshi、Forbidden Four）は日本人の稲葉 直貴（Naoki Inaba）によって製作されたパズルである。長方形のグリッドのいくつか白マスに○を配置し、全ての○が縦・横でひとつながりになるようにする。○は縦・横一直線に４つ以上連続してはいけない。

アイランド（Island、Tents Island、Airando）とは日本人の稲葉直貴に制作れた論理パズルである。グリッドの一部のマスにはヒント数字がある。マスを黒に塗ることによって、全体が縦・横で地続きになっている白マスの「島」の形を明らかにする。数字は、そこから自由に動ける土地の面積を表す。他の数字は乗り越えられない。

ドミニオン（Dominion）には一部のマスに文字が入っているグリッドがある。次のようなルールに従い、マスの一部を黒に塗る：

• 黒マスは２つずつしか配置しない。つまり、各２つの黒マスは縦・横につながっている。（そのつながっている２つのマスはドミノと言われる）。
• ドミノどうしは辺で接しない。
• 文字の数字は黒にならない。
• ドミノで区切られた領域を「国」と呼ぶ。国の全ての白マスは縦・横につながっている。
• 同じ文字は同じ国、違う文字は違う国に属する。
• 文字が入らない国ができてはいけない。

パーキング（Tren）とは日本人の青木しんいちに制作された論理パズルである。（盤面はパーリングで、ブロックは「車」である）。グリッドの一部のマスには数字が入っている。パズル面に1 × 2 マスまたは1 × 3 車を配置する。すべての車は数字のマスを１つだけ含む。また、車同士は重ならない。数字は、それを含む車の前後にある空白マスの合計数を表している。

No Four in a Rowとは形が決まっていない網である。その網にある枠のなかに×印と〇印がある。あいている枠は、横、縦、斜めは同じシンボルが並んで三つ以下でなければならない。

バッグ（Corral、Bag、Cave）には正方形の盤面がある。ゲームの目的は点線の上に縦横に線を引き、全体で１つの輪を作ることである。ヒント数字は、その数字から上下左右４方向にまっすぐ進み、輪の線にたどりつくまでの、その数字を含めてのマスの合計を表す。ヒント数字は、すべて輪の内側に入る。

フォーセルズ（Foseruzu、Four Cells）とは、四角形や長方形の網の枠のなかにある数字のパズルである。網は4つずつの枠のブロックに分ける。数字は、枠を４つに分けた時に他の枠と面するかずである。外枠も数に含まれる。一つブロックの中に入る数字は何でもよい。数字がない場合もある。

ファイブセルズ（Faibuseruzu、Five Cells、Solomon's Keep）とは、四角形や長方形の網の枠のなかにある数字のパズルである。網は5つずつの枠のブロックに分ける。数字は、枠を5つに分けた時に他の枠と面するかずである。外枠も数に含まれる。一つブロックの中に入る数字は何でもよい。数字がない場合もある。

ストレートクロス（Sutoreto、Sutoretokurosu、Straight Cross）は、日本の稲葉直樹によって作られたパズルである。それは白いと黒い枠が入る四角形や長方形の網である。ある白い枠の中に数字が書いてある。あいている白い枠は、横、縦に黒い枠の間に連続した数字が不規則に入る。例えば、2-3-4とか5-4-7-6。

連番（Renban）とは、不規則な形のブロックに分かれている四角形の網である。あいている枠は、網の各横列、各縦列、各ブロックの中に重複しないように連続した数字を入れる。例えば、5-3-4。

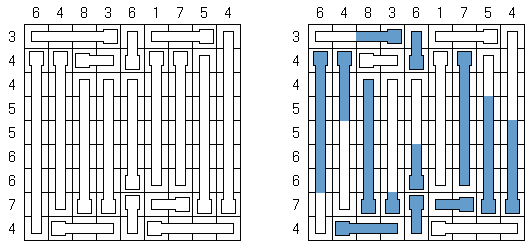
ブライトライト（Buraitoraito、Bright Light）とは、日本の稲葉直樹によって作られたパズルである。それは白と黒の枠が入っている四角形や長方形の網である。黒い枠の中に書いてある数字は、この枠の横、縦に並んでいる他の黒い枠や外枠までの☆印の数と合う。

イラストレーション（Irasuto、Irasutoreshon、Illustration）とは、日本の稲葉直樹によって作られたパズルである。それは白と黒の枠が入っている四角形や長方形の網である。ある枠の中に数字が書いてある。次の規則に基づいて、正しい順番に黒のと白の枠を移動させる。

• 白の枠の中に書いてある数字は、この枠の横、縦に並んでいる黒い枠や他の白の枠までの白の枠の数と合う。
• 黒の枠の中に書いてある数字は、この枠の横、縦に並んでいる他の黒い枠や白の枠までの白の枠の数と合う。

ナンバーブロック（Suguru、Nanbaburokku、Number Blocks）とは、日本の稲葉直樹によって作られたパズルである。それはブロックに分かれている四角形や長方形の網である。各ブロックの中に1からブロックに入る枠の数まで数字を書き込む。同じ数字が入る枠が横、縦、斜めに繋がれない。

トリヌド（Trinudo）とは四角形や長方形の網である。ある枠の中に数字が書いてある。網は1、2、3つずつの枠のブロックに分ける。同じサイズのブロックは横、縦に繋げられない。ブロックの各数字は、そのブロックの枠の数を表示する。

クリーク（Kuriku、Creek）は四角形や長方形の網である。線が交差されている所に丸で囲まれた0~4の数字がある。その数字は丸に接している黒い枠の数である。白い枠は全部横、縦に繋がるように順番に黒い枠と白い枠を移動させる。

ガッピ（Gappy）は四角形の網である。各横、縦列に黒い枠が二つ残るように移動させる。黒い枠は斜めや隣どうしにならない。枠外の数字は二つの黒い枠の間にある白い枠の数を表示する。

のりのり（Norinori）はパズルの種類の一つであり、自由な形の部分に分かれた四角形や長方形の網である。各部分に二つの枠を塗りつぶす。塗りつぶした枠は部分の境の線に関わらず横、縦の二つずつの枠(ドミノ)である。黒い枠は隣どうしにならなず、斜めに繋いでもよい。

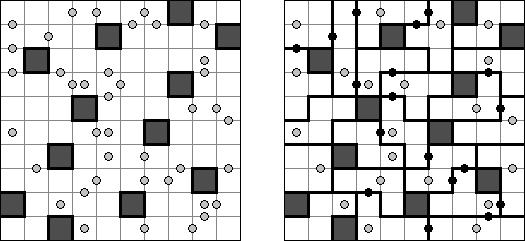
４マス分割（Yonmasu、Yonmasubunkatsu）は、日本の稲葉直樹によって作られた四角形や長方形の網のパズルである。ある枠に丸がある。枠を、丸が一つ入っているように四つずつに分ける。

ブリックス（Bricks）はパズルの種類の一つである。枠を、各横、縦列に繰り返さないように数字を記入する。各ブリックは偶数と奇数である。

ナンバーチェーン（Number Chain）は、ロシアのレオニード・モチャーロフ(Leonid Mochalov)に作られたパズルである。四角形や長方形の網であり、各枠に数字が入っている。一番上の左の枠は1、一番下の右の枠はN(何かの数字)であり、その以外の枠は1とNの間の数字が書いてある。一番上の左の枠から一番下の右の枠までの線を引く。その線が通る枠の数はNの数字になるようにして、数字は繰り返さないようにする。

セットカーペット（Kapetto、Settokapetto、Set Carpets）は、日本の稲葉直樹によって作られた四角形や長方形の網のパズルである。ある枠に数字がある。枠を、数字が一つ入っているように長方形の部分に分ける。その数字は枠の数である。各部分に入っていない枠がある。

連カツ（Renkatsu）は、日本の稲葉直樹によって作られた数字が含まれた四角形や長方形の網のパズルである。1からN数字までの部分に網を分ける。N数字は枠の数である。

Eulero（Graeco-Latin Square、Euler Square） は文字と数字が含まれたパズルである。次のルールを守るように四角形の網を記入する。

• 各枠は文字、数字が一つずつある。
• 各横、縦列は文字、数字は繰り返さない。
• 文字と数字の組み合わせは繰り返さない。

アンライクモザイク（Anraikumozaiku、Unlike Mosaic）は、日本の稲葉直樹によって作られた四角形や長方形の網のパズルである。ある枠に丸がある。枠を、丸が一つ入っているように長方形の部分に分ける。その部分は黒い枠を含めない。同じ数の枠の部分は横、縦に繋がれない。

クロット（Kurotto）はパズルの種類の一つである。四角形や長方形の網は、ある枠には数字が入っている丸や入っていない丸がある。次のルールを守るように白、黒い枠を移動させる。

• 丸が入っている枠は黒い枠にならない。
• 黒い枠は横、縦に繋いでもよい。
• 丸の中にある数字はその枠に繋がる黒い部分の枠の数である。
• 数字が入っていない丸の枠に黒い枠はいくつあってもよい。

たすくえあ（Tasukuea）はパズルの種類の一つである。四角形や長方形の網は、ある枠には数字や疑問符がある。次のルールを守るように白、黒い枠を移動させる。

数字や疑問符が入っている枠は黒い枠にならない。

• 黒い枠は四角形の部分を結成する。
• 黒い枠の部分は横、縦に繋がられない。
• 数字はその枠に横、縦に繋がる黒い部分の枠の数である。
• 疑問符が入っている枠に黒い枠は一つ以上繋がれる。
• 白い枠は全て横、縦に繋がれる。

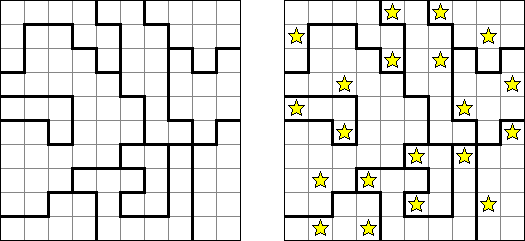
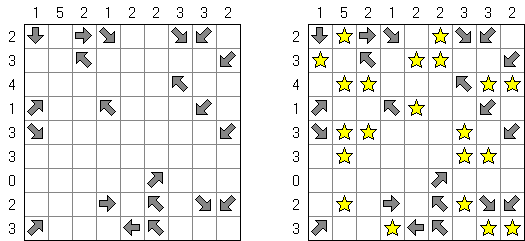
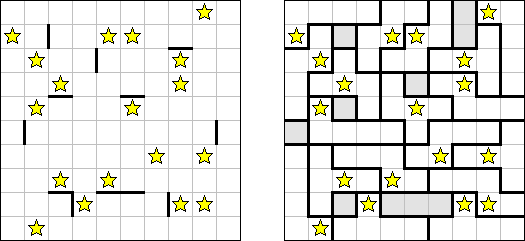
Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.

Araf (from Turkish, literally "purgatory"; original Japanese name - 相ダ部屋) is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.

カービングロード（Kabingurodo、Curving Road）は、日本の稲葉直樹によって作られた四角形や長方形の網のパズルである。ある枠に丸がある。次のルールを守って網の黒い枠を移動させる。

• 丸が入る枠は黒色にならない。
• 黒い枠は斜めにだけ繋がられる。
• 白い枠は全て横、縦に繋がれる。
• 丸の間の白い枠を通る道は2回以上曲がる。

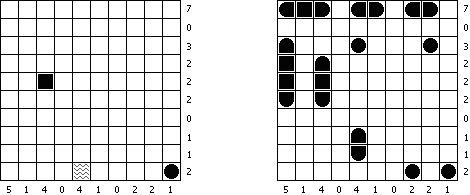
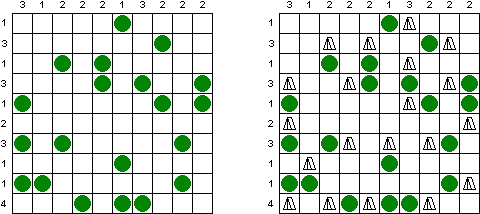
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.

へび （Snake、Tunnel） is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.

ペイントエリア （Peintoeria、Paint Area） is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All cells of a region must have the same color.
• A cell with a number indicates how many black cells are adjacent to it.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the same color.

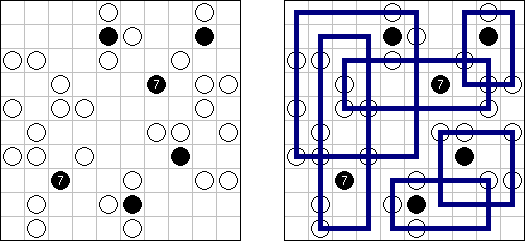
Ｉループ （Irupu、I-Loop） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.

さしがね （Sashigane） is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.

さしカズね（Sashikazune） is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

チョコナ（Chocona、Chocolate） consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any number of cells may be blackened.
• The black cells must form rectangles, independently of the region borders.
• The black rectangles must not be orthogonally adjacent.

Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.

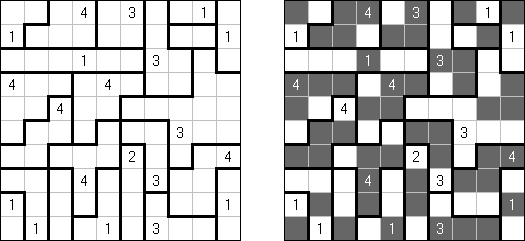
ヌルオミノ （LITS、Nuruomino） is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.

The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.

ナンバーボール （Nanbaboru、Number Ball） consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.

タイルペイント （Tairupeinto、Tile Paint、Crazy Pavement） consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.

Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.

ナンロー （Nanro） is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.

Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.

アルコネ（ナンバーリンク、Arukone、Number Link） consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.

テトロイド（Tetroid） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

スキマブロック（Sukima、Sukimaburokku） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.

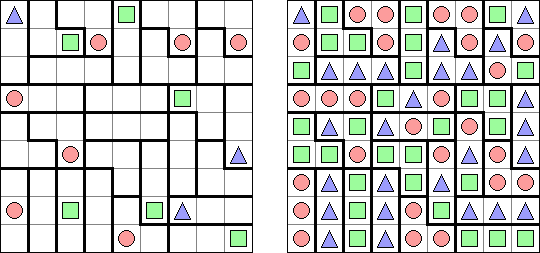
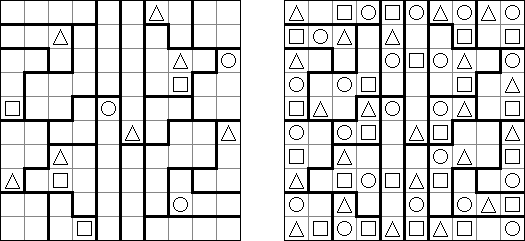
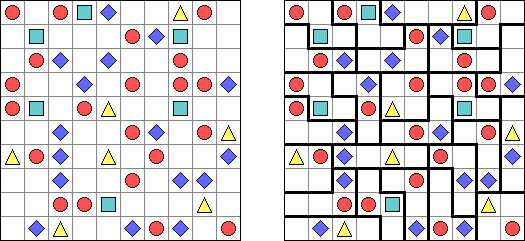
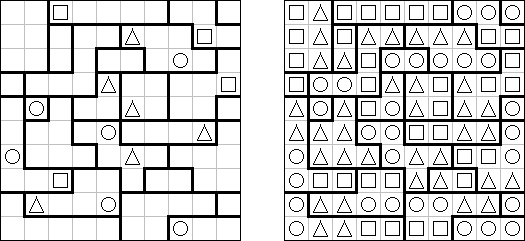
ワンｏｒオール（Triplets、One or All） is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.

コレクトコネクト（Korekutokonekuto、Correct Connection） is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.

Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.

フリースリー（Furisuri、Free Three） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.

ヤギとオオカミ（Yagit） is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.

プレーンループ（Purenrupu、Pure Loop） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.

フィルマット（Firumatto、Fillmat） is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.

なわばり（Nawabari、Territory） is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.

マカロ（Makaro） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.

ドッスンフワリ（Dosun-Fuwari） is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:

• White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle.
• Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.

さとがえり（Satogaeri） is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.

コブリン（Koburin） is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.

Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.

シロクロリンク（Shirokuro） is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.

ろーま（Roma） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.

ボーダーブロック（Bodaburokku、Border Block） is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.

クロシュート（Kuroshuto、Kurochute） is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.

遠い誓い（Toichika） is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:

• Each region contains exactly one arrow.
• Each two arrows are paired, they point to each other. There are no unpaired arrows.
• Two regions with paired arrows must not be horizontally or vertically adjacent.
• Between two paired arrows no other arrow must be placed.

ウソタタミ（Usotatami） is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.

パイプリンク（Pipelink） consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.

はこいり（Hakoiri） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.

ぬりぼう（Nuribou） is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• The black cells divide the grid in areas of white cells. Each area contains one cell with a number.
• Each area must have the same number of white cells as the number it contains (including the numbered cell).
• Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide.
• If two stripes are connected diagonally, the length of the stripes must be different.

タタミバリ（Tatamibari） is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.

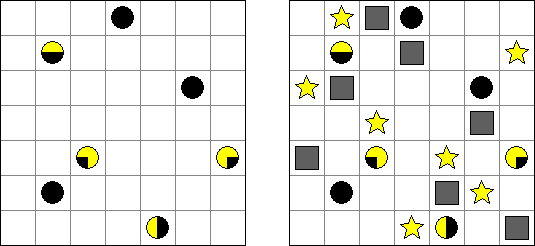
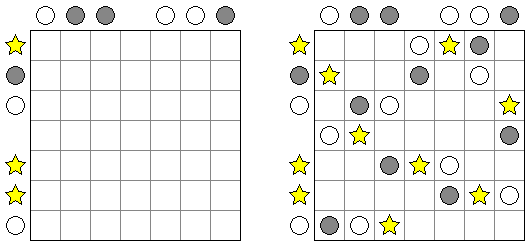
ムーンライト（Sun and Moon） is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.

コージュン（Kojun） is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.

ウソワン（Usowan） is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells).
• Two black cells must not be orthogonally adjacent.
• All of the white cells must be connected.

ごきげんななめ（Gokigen Naname、Slalom） is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.

へびいちご（Hebi-Ichigo） is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:

• Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake").
• Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed.
• Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached.
• The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.

Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

玉石混交プレース（Gyokuseki） is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.

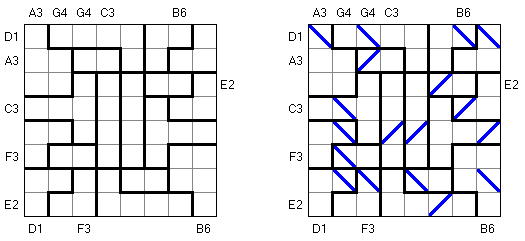
キンコンカン（Kin-Kon-Kan） is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.

イチマガ（Ichimaga） is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.

島国（Shimaguni） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• Two regions with the same amount of black cells must not be orthogonally adjacent.
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.

やじさんかずさん（Yajisan-Kazusan） is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:

• Black cells must not be orthogonally connected.
• A cell with a number may be blacken.
• All the white cells must form an orthogonally continuous area.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.
• Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.

へびのあな（Snake Pit） consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:

• A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally.
• A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all.
• A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells.
• Two snakes of the same length must not be orthogonally adjacent.
• A cell with a cross cannot be an end of a snake.

碁石ひろい（ごいしひろい、Hiroimono、Goishi Hiroi） is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:

• Start at any stone.
• When a stone is encountered, it is picked up.
• When a stone is picked up, the direction can be changed.
• It is not allowed to reverse the direction.

Water Fun is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.

Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.

Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.

サントイッチ（Santoitchi、３と１） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• All white cells must be divided on regions having the size of exactly three cells.
• Two black cells must not be orthogonally adjacent.
• Each region contains a number.
• A number indicates how many black cells share an edge with that region.

ハムサンド（Hamusando、Ham Sandwich） is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.

Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.

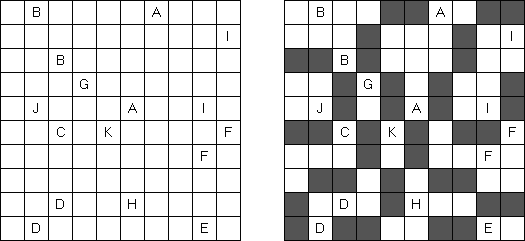
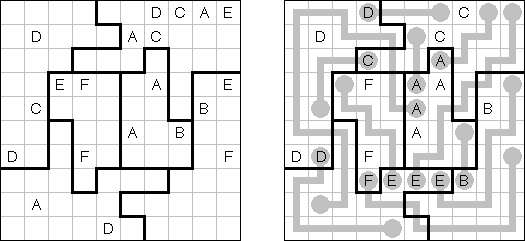
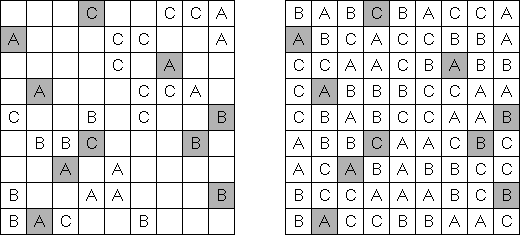
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.

数コロ（Sukoro） consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.

EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.

Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.

クロシロループ（Kuroshiro、Kuroshirorupu） is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.

月か太陽（Moonsun、Moon or Sun） is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.

四角スライダ（Rectslider、Rectangle-Slider） consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

ストストーン（Stostone、Stone on Stone） is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:

• All black cells in a region must be connected horizontally or vertically.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• If all stones "fall down", they must cover exactly the bottom half of the grid.

コーヒー牛乳（Kohi Gyunyu、Coffee Milk） consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.

ミルクティー（Mirukuti、Milk Tea、Milk-T） consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.

スラッシュパック（Slash Pack） is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.

ぬりめいず（Nurimaze、Nurimeizu） consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:

• Cells with letters, circles or triangles are always white.
• White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide.
• A path from S to G includes all cells with circles and no cells with triangles.
• No 2 x 2 cell area within the grid can have the same color.
• All white cells must form an orthogonally continuous area.
• White cells must not form a loop.

Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:

• All black cells create a single connected group.
• No 2 x 2 cell area within the grid can contain all black cells.
• Numbered cells must not be black.
• Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.

カントリーロード（Country Road） is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.

ノンダンゴ（Nondango） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:

• Each region contains one black circle.
• Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.

ミントネット（Mintonette, the original name of the game known as volleyball） is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.

Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.

Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.

はなれ組（Hanare、Hanaregumi） is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.

Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)

Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.

Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.

環状線スペシャル（Kanjo、Kanjo-sen supesharu） is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.

るっくえあ（Rukkuea、Look-Air） is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:

• Black cells form an area of square shape.
• No black areas touch each other horizontally or vertically (only diagonally).
• Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size.
• Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.

ゴーレム・グラッド (Golem Grad, an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:

• The black cells divide the grid into areas of white cells ("islands"), each containing at most one number.
• Two islands may not be connected.
• The island must have the same number of white cells as the number it contains.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the black color.
• All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid.
• Snakes must not cross each other.

Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:

• No two horizontally, vertically or diagonally adjacent cells contain a digit.
• The numbers across the top and down the left equal the row and column totals for the cells with numbers.
• The numbers across the bottom and down the right are the sums of numbers in the rows and columns.

覆面ウォールロジック（Hukuwall） is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.

ぬりみさき（Nurimisaki） is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• White cells form a path exactly one cell wide.
• Cells with circles are always white.
• A cell with a circle must have exactly one white cell adjacent to its side.
• A white cell without a circle must have at least two orthogonally adjacent white cells.
• A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself.
• All the white cells must be connected horizontally or vertically.
• No 2 x 2 cell area within the grid can have the same color.

ニア・プレース（Starry Night、Niapuresu、Near Place） is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:

• The white circle indicates that the sun is closer to the star than the moon.
• The black circle indicates that the moon is closer to the star than the sun.
• The star outside the grid indicates that the circles are at equal distance from the star in that row or column.

同異なえる（Douieru） is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.

テトロン（Tetoron） is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.

差で四角（Sashikaku） is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.

ヘキサンナ（Heki） is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.

Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)

デッドアングル（Deddoanguru、Dead Angle） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.

エンドライン （Endorain、End Line） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.

Nuraf （Araf Nurikabe） combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells divide the grid into areas of white cells ("islands").
• Cells with numbers are always white.
• Two islands may not be connected.
• All of the black cells must be connected.
• No 2 x 2 cell area within the grid can have the black color.
• Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.

みち（Miti） is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.

アローフロー（Arofuro、Arrow Flow） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.

• The same arrows cannot be placed in adjacent cells.
• Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached.
• A cell with a number indicates a total number of arrows that leads to this cell.

Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.

モビリティ（Mobiriti、Mobility） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.

ムーブナンバー（Mubunanba、Move Number） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.

Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)

リモートエッジ（Rimotoejji、Remote Edge） is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.

Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.

ワームズ（Wamuzu、Worms） is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.

お家へ帰ろう（Kaero） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.

Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.

ユニークマーカー（Yunikumaka、Unique Marker） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.

Meandering Numbers (also known as "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)

容器分割（Yokibunkatsu） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.

スクリン（Scrin、Screen） is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.

From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.

信号機（Shingoki） is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.

Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.

Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.

ネイバードミノ（Neibadomino、Neighbour Domino） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)

ジェミニブロック（Jemini、Jemini Block） is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.

ダブルチョコ（Double Choco） is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).

コーナーループ（Konarupu） is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.

ガイドアロー（Gaidoaro、Guide Arrow） is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).

ミッドループ（Mid-Loop） is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.

ドッチループ（Dotchi-Loop） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.

Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.

Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.

Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.

Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.

SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.

ちようつがい（Chiyotsui） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border.
• A cell with a number indicates how many cells in the region must be blackened.
• No two black areas may share an edge.

エーカー（Aqre） is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.

Geradeweg (Straight Loop) is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.

クロクローン（Kuroclone） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

やじさんそうこばん（Yajisan-Sokoban） is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.

Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.

らねこマップ（Raneko） is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.

Factorism （Find the Factors） is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.

アーキペラゴ（Akiperago） is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:

• The black cells form "islands". No two islands may share an edge; islands may be connected through their corners.
• If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island).
• All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners.
• If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).

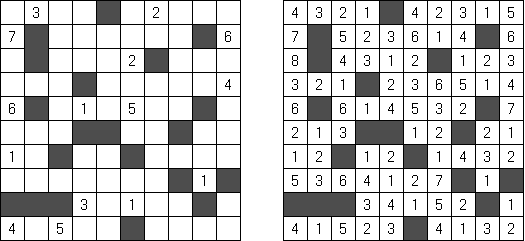
Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.

ミラーリングタイル（Miraringutairu、Mirroring Tile） is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

へやブロ（Heyablock、Heyawake-Block） is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All white cells form one orthogonally connected area.
• A line of connected white cells cannot go through two or more region borders.

チョコバナナ（Choco Banana） is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.

わたりどり（Wataridori） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.

チェンブロ（Chenburo、Chain Block） is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally).
• A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer.
• Each block contains exactly one number or a question mark.
• All blocks form "chains". A chain is a group of two or more blocks, connected through their corners.
• Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.

ワンルームワンドア（Wanrumuwandoa、One Room One Door） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened.
• Blackened cells should not share an edge.
• All the white cells must be connected inside a region (it's possible for a region to have no white cells).
• If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions.
• All the white cells must form an orthogonally continuous area.

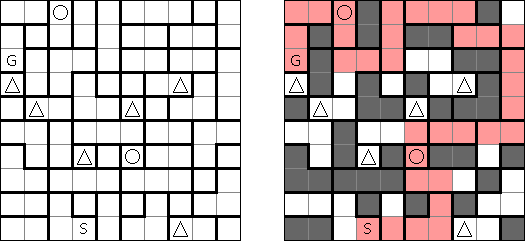
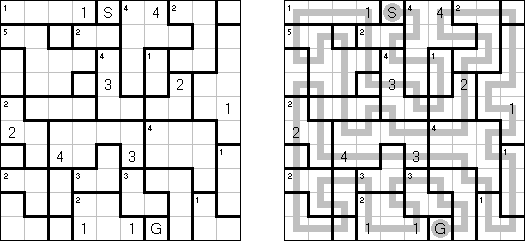
Haisu （House） is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its N^th entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.

オービタル（Obitaru、Orbital） is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.

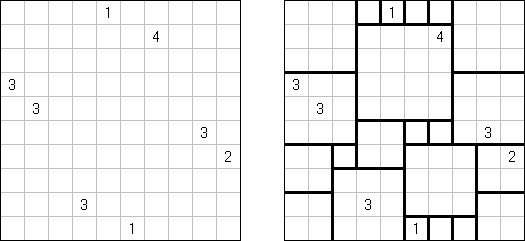
Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.

カクテルランプ（Kakuteruranpu、Cocktail Lamp） is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected horizontally or vertically (they form a "block").
• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any amount of cells may be blackened (all cells may stay white).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All blocks of black cells must be connected to each other through their corners.
• No 2 x 2 cell area within the grid can contain all black cells.

家族写真（Kazoku、Kazoku shashin） is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.

とんとんべや（Tontonbeya） is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.

Context is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:

• All the white cells must be connected horizontally or vertically.
• A cell with a number can be blacken. Two black cells must not be orthogonally adjacent.
• The number in a white cell indicates the number of orthogonally adjacent black cells.
• The number in a black cell indicates the number of diagonally adjacent black cells.

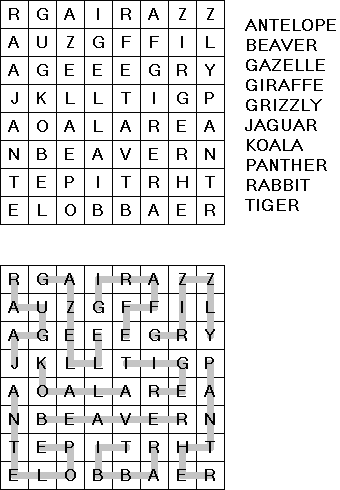
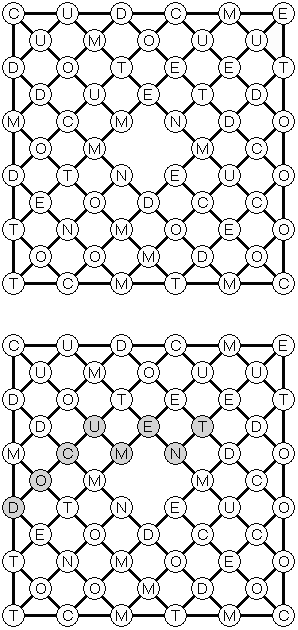
ワードファインダー（Word Finder、Word Search、Word Seek、Word Sleuth、Mystery Word）には文字が入っている長方形のグリッドがある。グリッドの中に隠された単語を見つけるのはゲームの目的である。単語がジグザグに書いてある。ジグザグは直角だけに曲げる。単語は重ならない。

パズルを制作するために単語リストを作る。パズルを解けた後残っている文字からできているキーワードを指定する機能もある。

9つの文字はワードファインダー (Word Finder)のパズルの種類である。横、縦に3ずつに分けられた文字が入っている網であり、その部分に隠れた9文字の言葉を見つける。

くもの糸 (Spider Web)は線で繋がれた丸からできているパズルである。丸の中に文字がある。キーワードの文字が入っている丸の連続性を見つける。

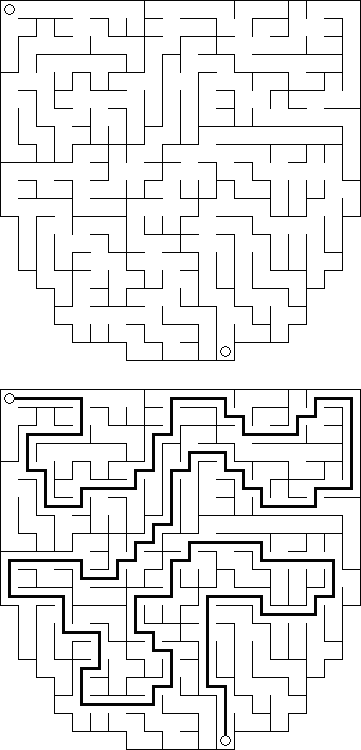
迷路(Maze)は、迷いやすい道の組み合わせのパズルである。二つのマークされた点の間の繋がれる道を見つける。コンピューターソフトは長方形や四角形だけではなくてどんな形の迷路も作れる。