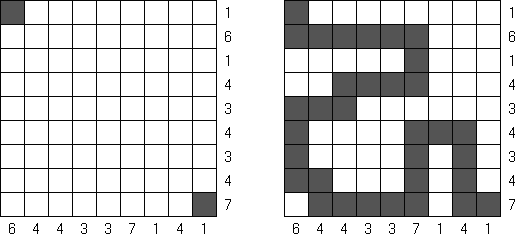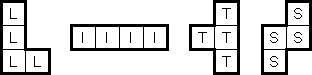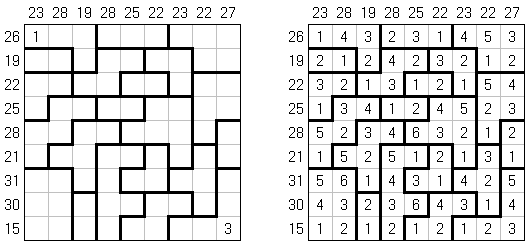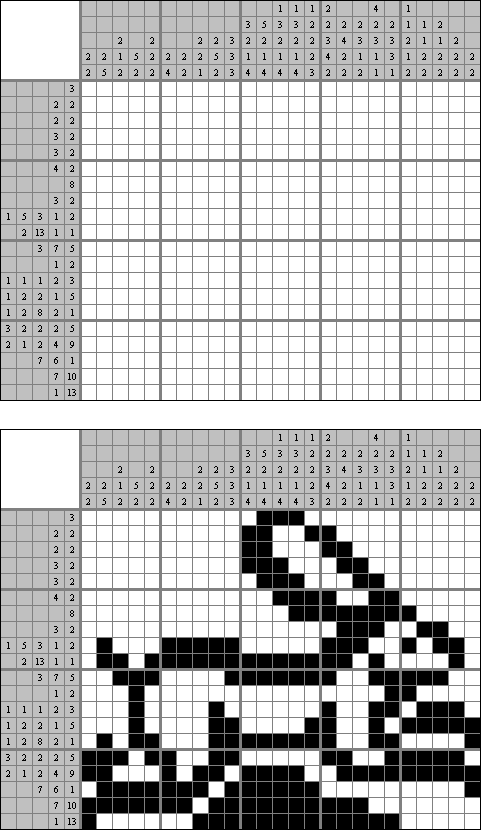
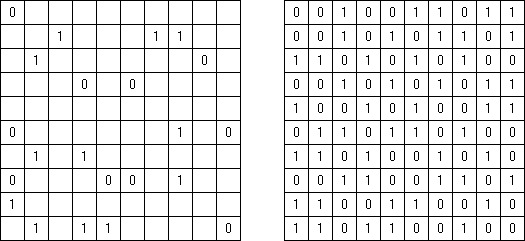
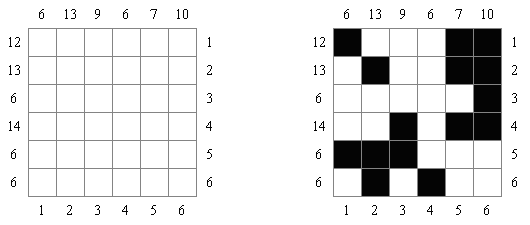
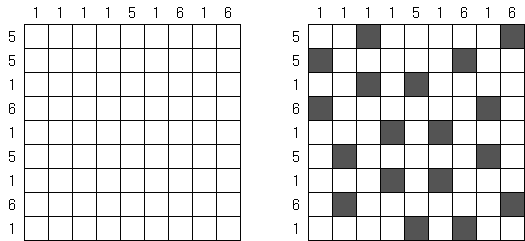
Cross+A 퍼즐들

Cross+A는 여러가지 논리 퍼즐(로직 퍼즐)을 풀고 생성한다. 만든 퍼즐은 이미지 파일(지원 형식: BMP, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF, Windows 메타파일, CorelDRAW 파일)로 저장이 가능하다. 또한 퍼즐은 일괄 처리 방식으로 만들 수 있다.

Nonogram (네모로직, "Hanjie", "Griddler", "CrossPix", "Paint By Numbers")은 힌트 숫자를 사용해 그림을 맞추어야 하는 정사각형이나 직사각형이다; 행의 왼쪽과 열 위에 있는 숫자는 해당 행에 검은 칸의 그룹이 몇 개가 있고 각 그룹에 연속적인 검은 칸이 몇 개가 포함되어 있는지를 보여 준다. 각 그룹은 적어로 하나의 빈 칸으로 나뉘어져 있다.

Cross+A은 흑백 퍼즐만 아니라 여러 색상이 사용되는 과제를 풀 수 있다.

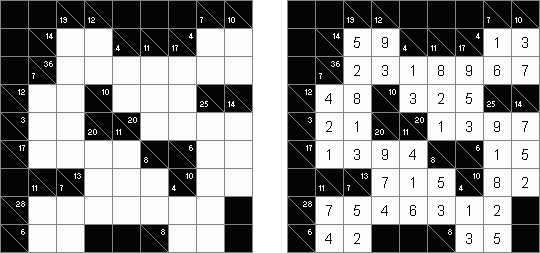
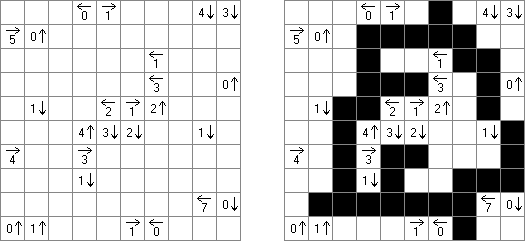
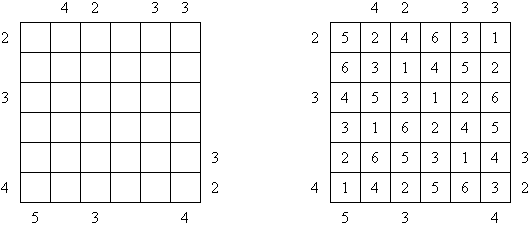
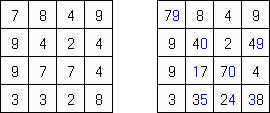
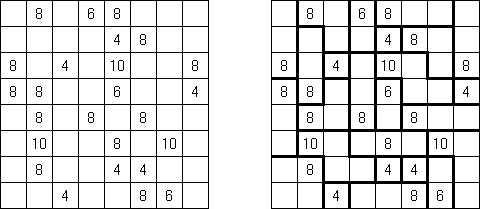
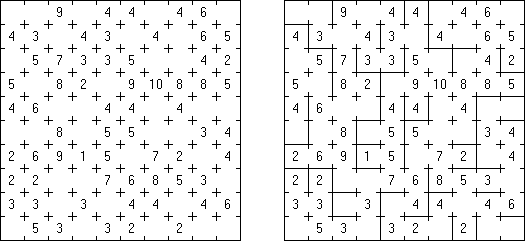
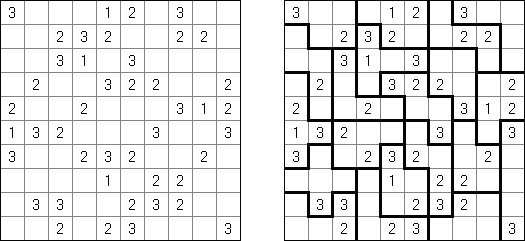
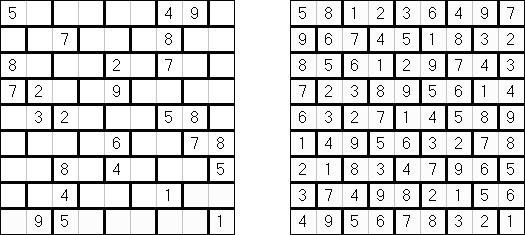
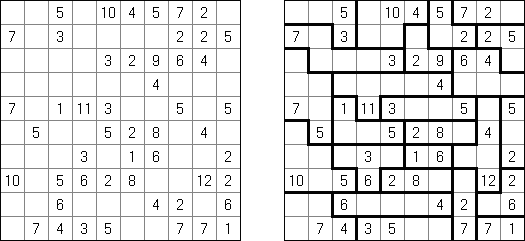
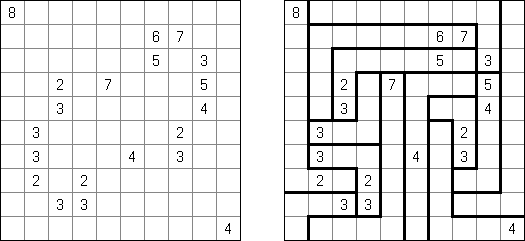
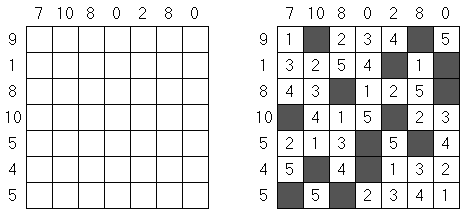
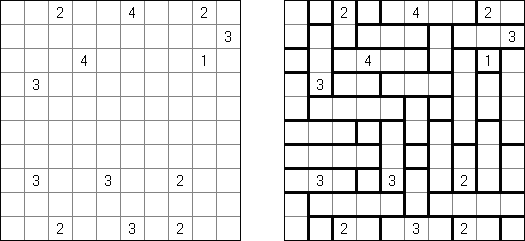
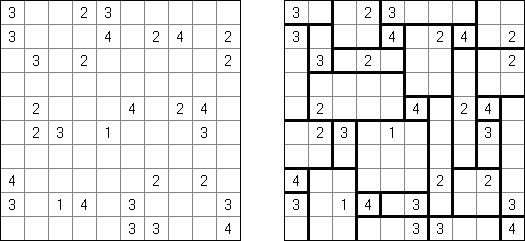
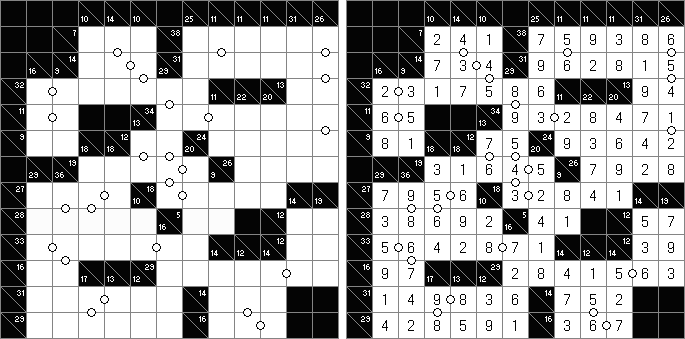
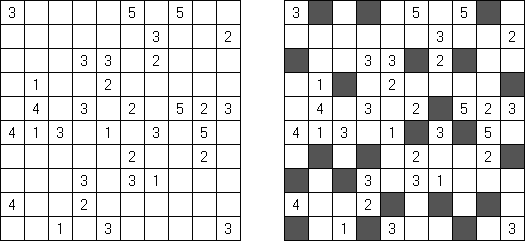
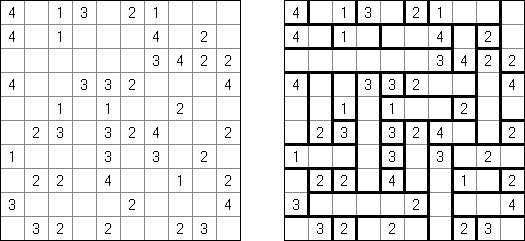
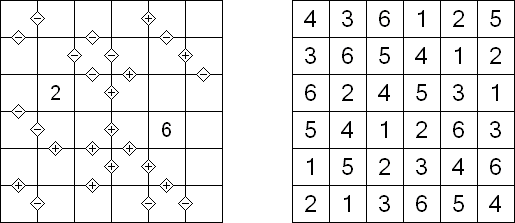
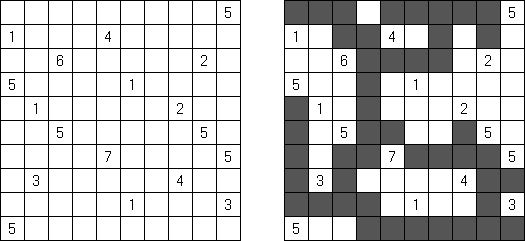
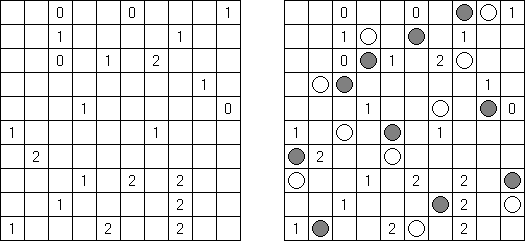
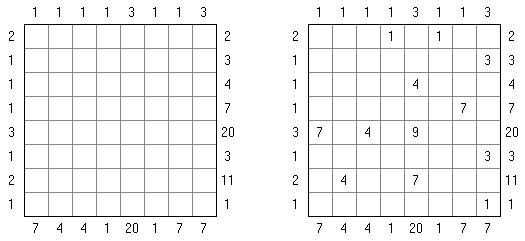
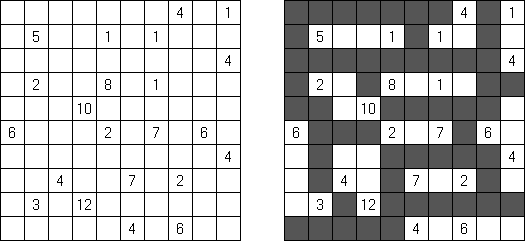
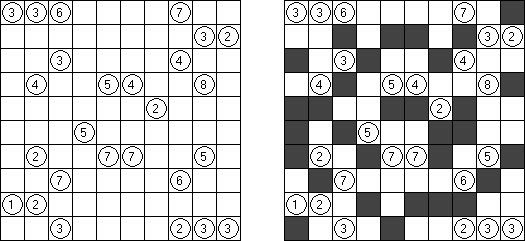
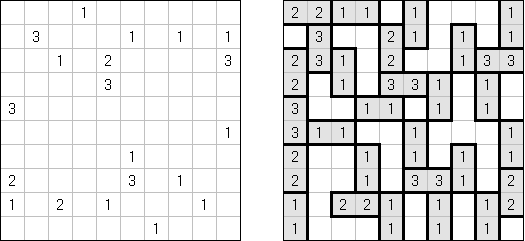
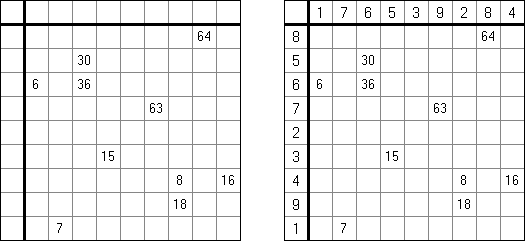
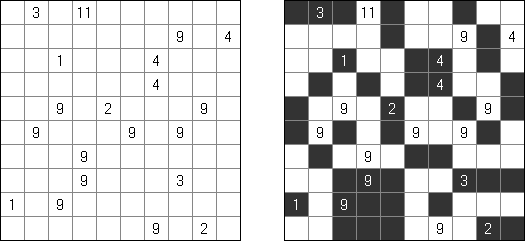
Kakuro (가쿠로)는 숫자 퍼즐이고 낱말 맞추기의 수학적 동등물이다. 목적은 흰 칸에 1부터 9까지의 숫자를 넣는 것이다. 숫자가 있는 칸에 오른쪽 위의 값은 행 숫자들의 합을 뜻하고 왼쪽 밑의 값은 본 칸 아래에 있는 열 숫자들의 합계와 같다. 예를 들어, 6을 1과 5 또는 2와 4의 합계로 표시할 수 있지만 같은 숫자 (3과 3)를 사용해서는 안된다.

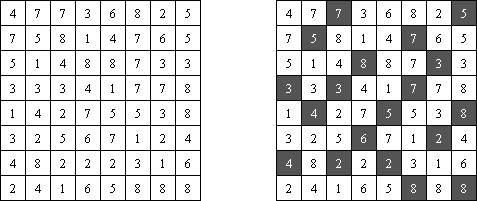
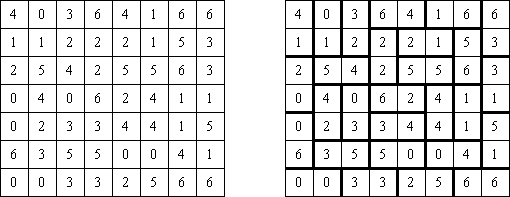
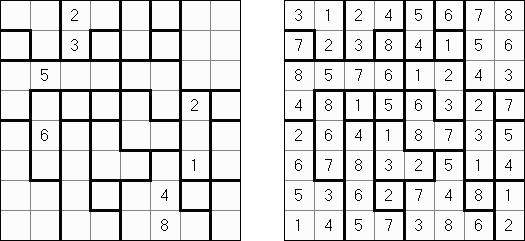
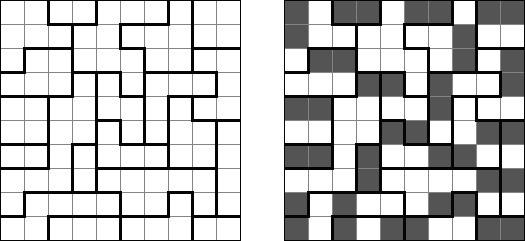
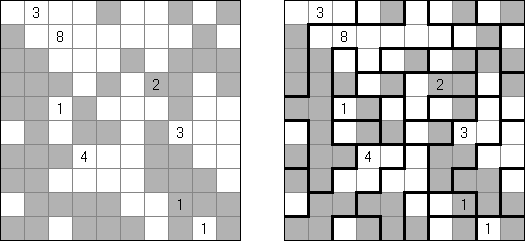
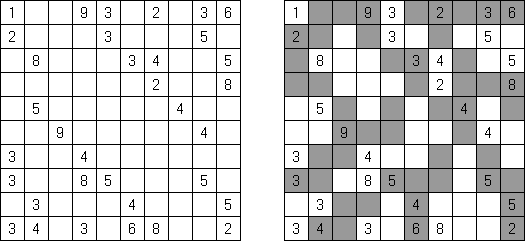
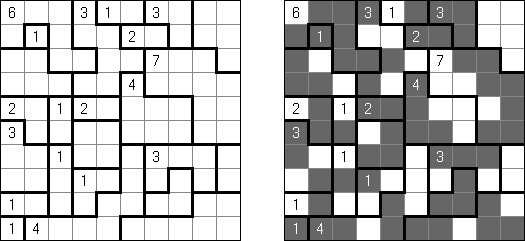
Hitori (히토리)는 논리 퍼즐이다. 목적은 아무 행이나 열에 같은 숫자가 한번 이상 나오지 않도록 중복되는 숫자를 지우는 것이다. 지운 칸의 모서리가 서로 접촉하면 되는데 지운 칸의 측면이 서로 접촉해서는 안 된다. 안 지운 칸이 지속적인 ‘흰색’ 공간을 구성해야 하고 즉, 이것 중에 하나라도 다른 같은 칸으로부터 격리되어서는 안 된다.

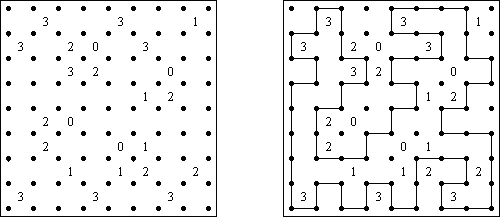
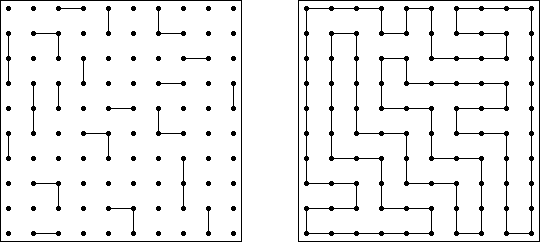
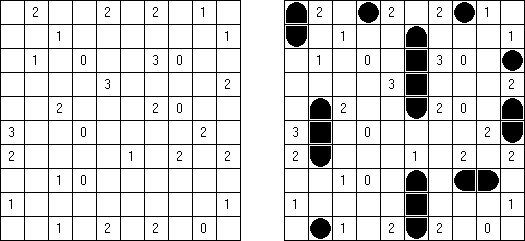
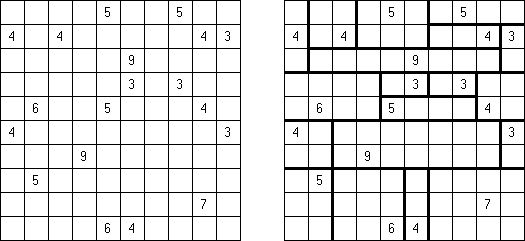
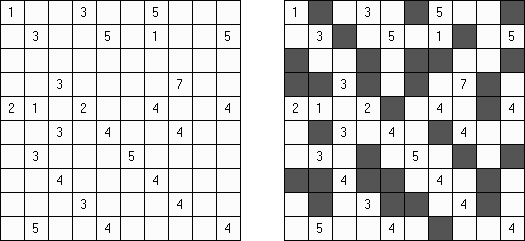
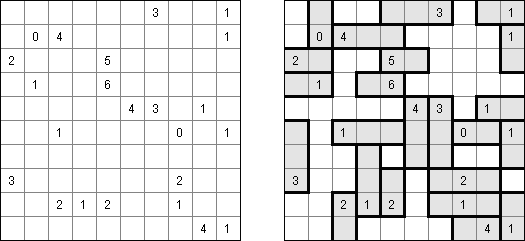
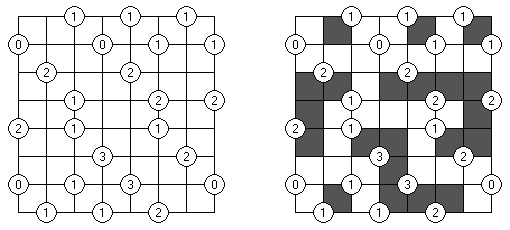
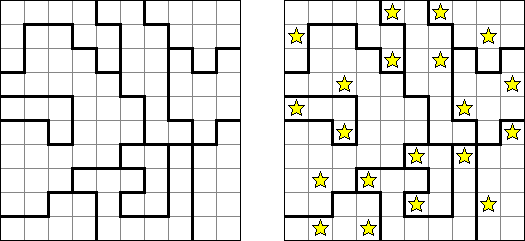
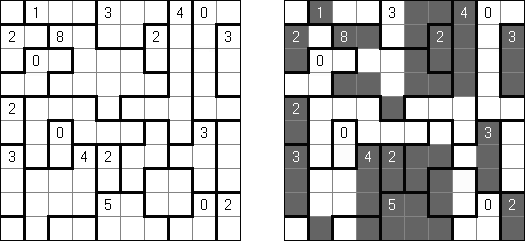
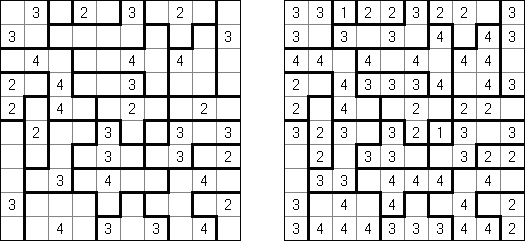
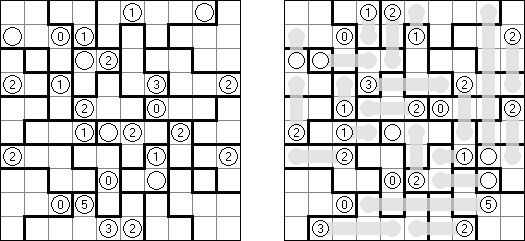
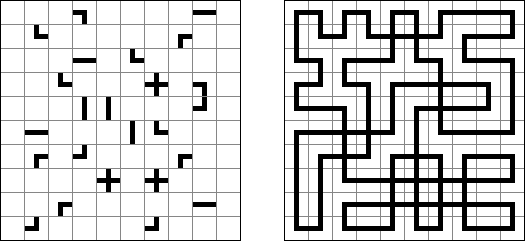
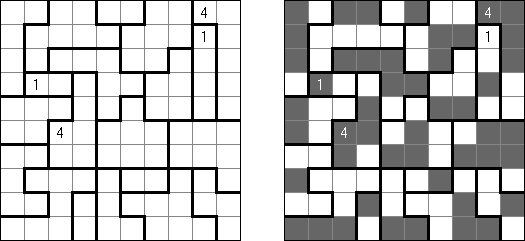
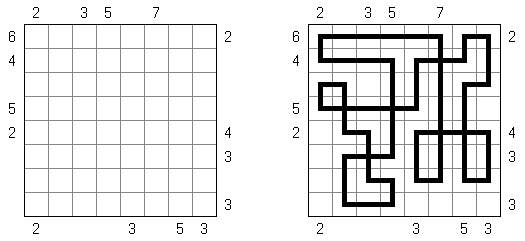
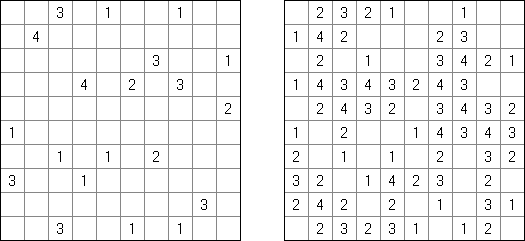
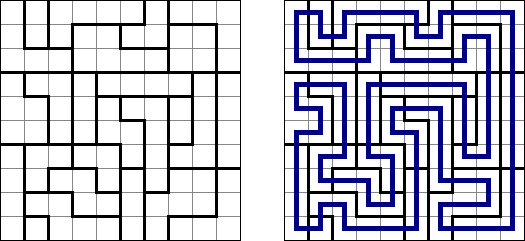
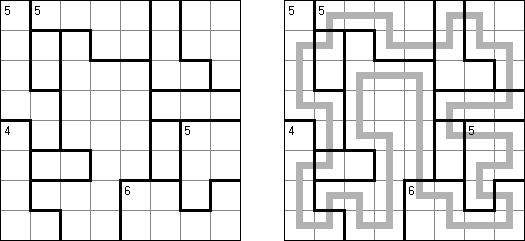
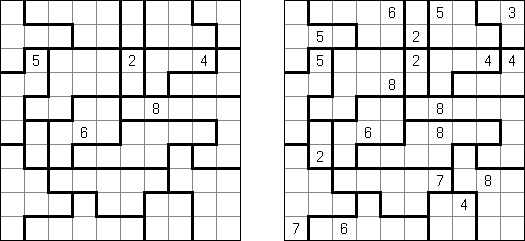
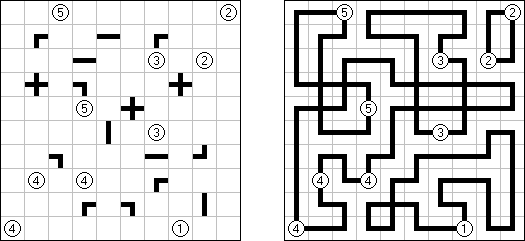
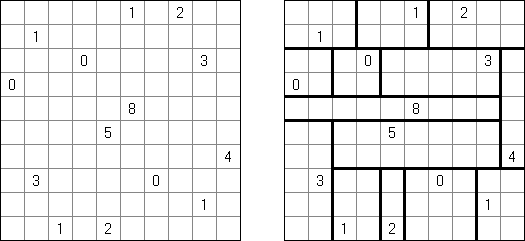
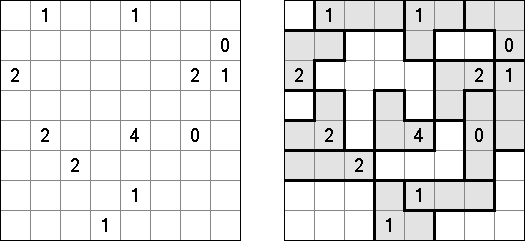
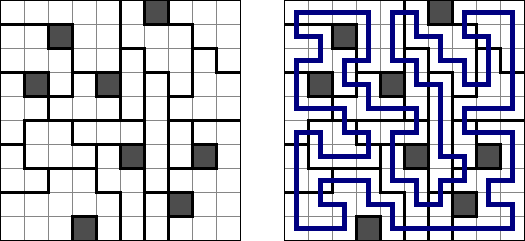
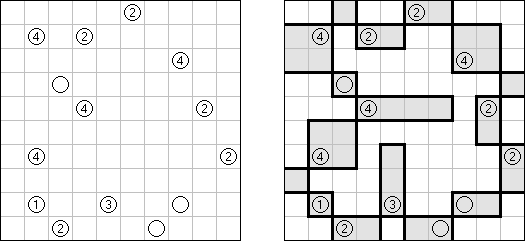
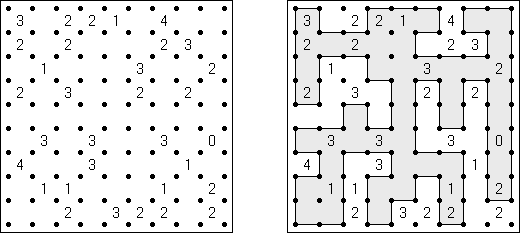
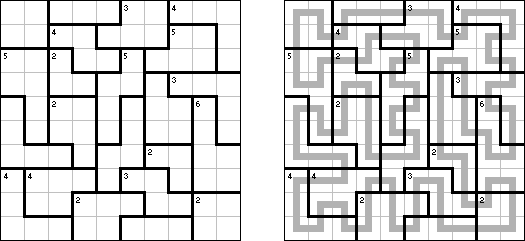
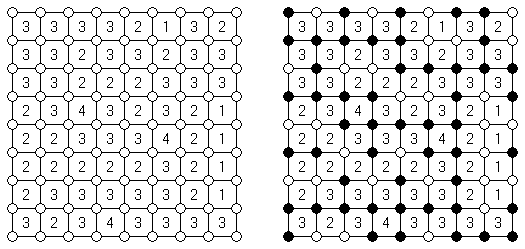
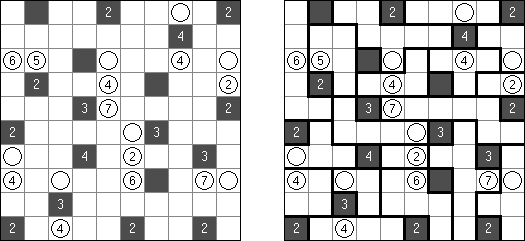
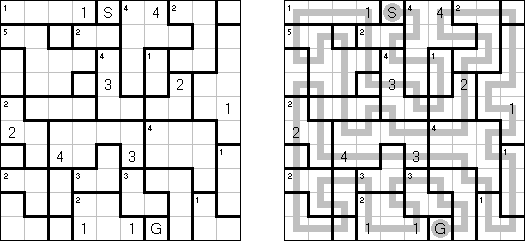
Slitherlink (슬리더링크, "Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin")는 미로 같은 논리 퍼즐이다. 목적은 자체를 교차하지 않는 하나의 폐쇄 회로가 되도록 점들을 가로세로 직선으로 연결하는 것이다. 각 숫자는 주위에 직선 몇 개가 있어야 하는지를 나타낸다. 칸에 숫자가 없는 경우에 이것 주위에 직선이 몇 개가 있는지 상관 없다.

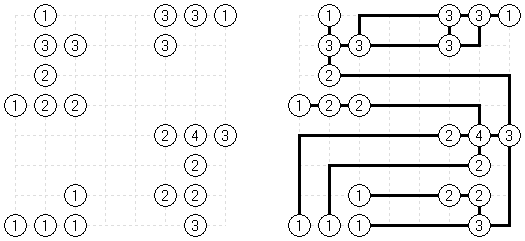
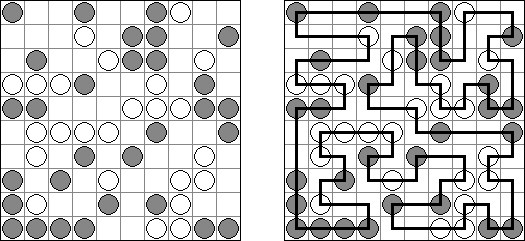
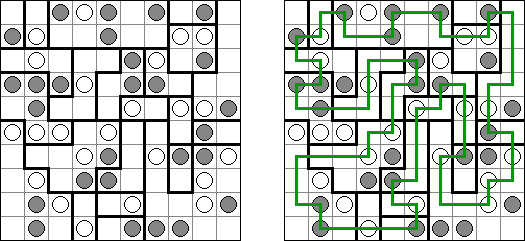
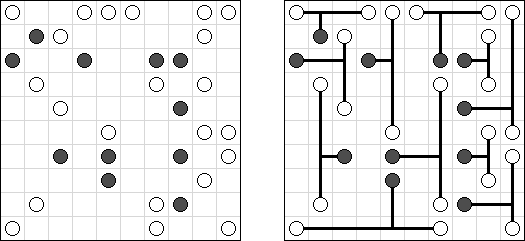
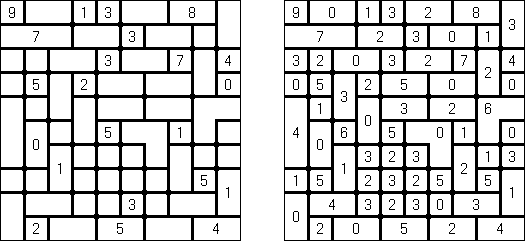
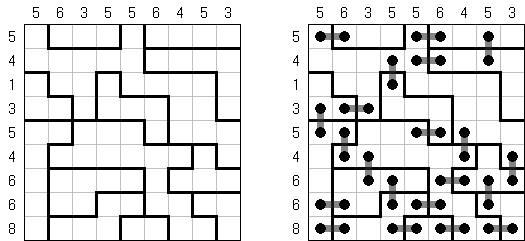
Link-a-Pix ("Paint by Pairs")는 숫자 퍼즐이다. 1을 제외하고 격자에 있는 모든 숫자가 쌍이 있다. 목적은 각 숫자 쌍을 찾아서 선으로 연결하는 것이다. 칸의 수는 선 끝에 있는 숫자들과 같아야 한다. 쌍을 연결하는 선이 편향하고 세로가로 갈 수 있는데 대각선 반향으로 가면 안 된다. 줄은 서로 교차하거나 같은 칸을 통과해서는 안 된다.

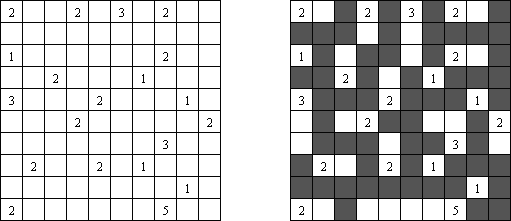
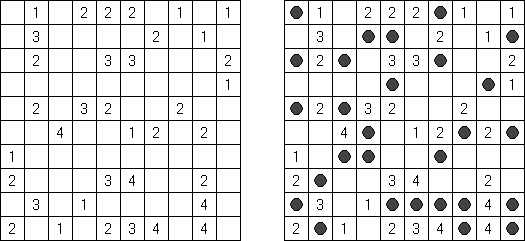
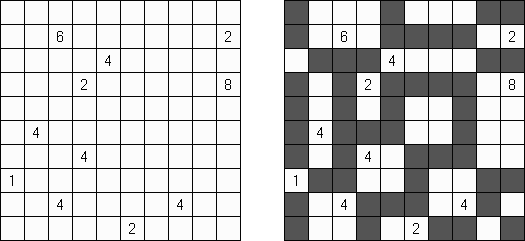
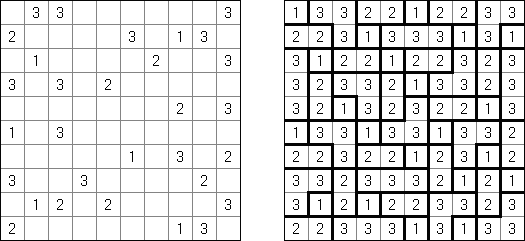
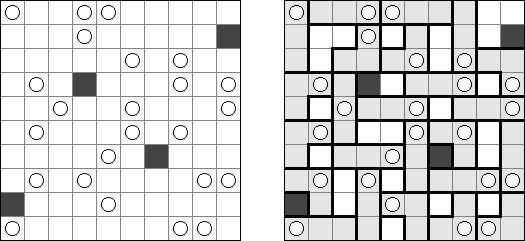
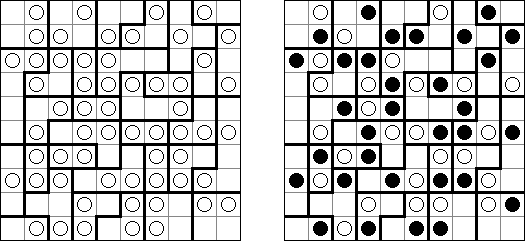
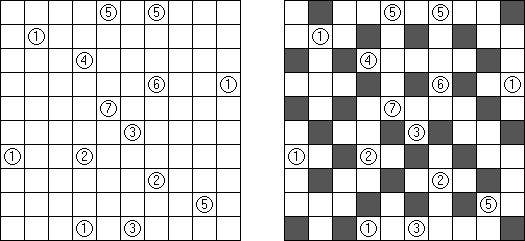
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In")는 숫자로 그림이 암호화된 논리 퍼즐이다. 각 숫자는 몇 개의 인접 칸(숫자가 있는 칸 포함)이 색칠되어야 하는지를 뜻한다. 예를 들어, 칸에 0이 있으면 이 칸도 인접 칸도 색칠되지 않을 것이다.

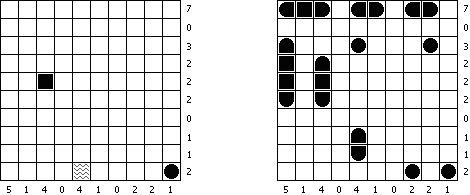
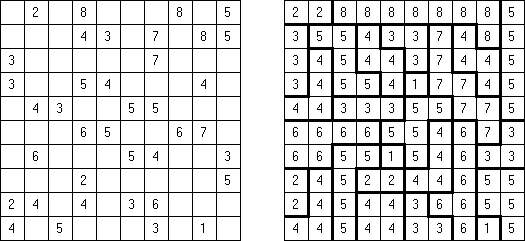
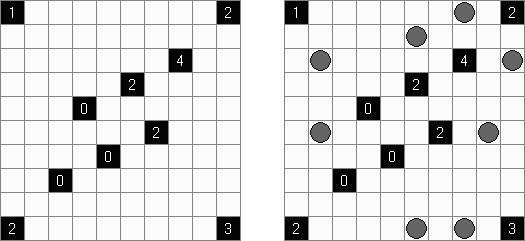
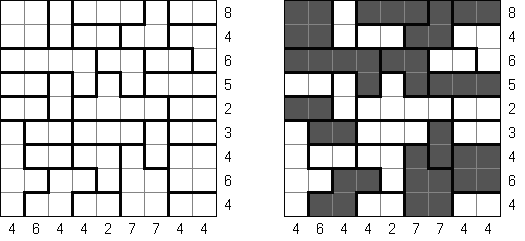
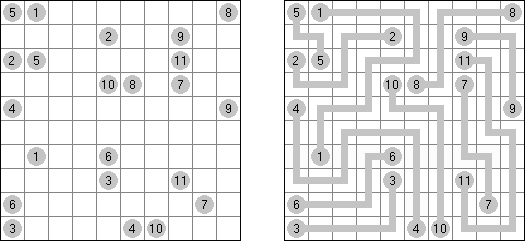
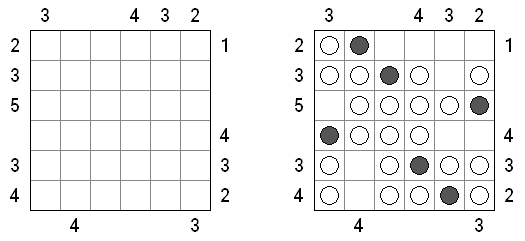
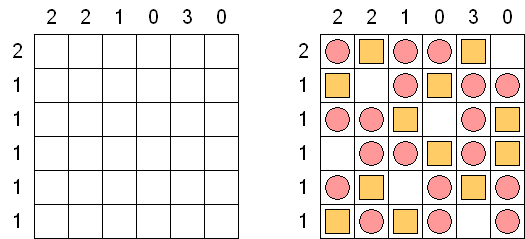
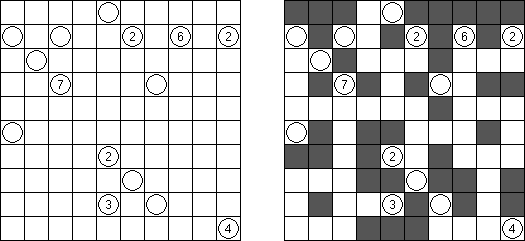
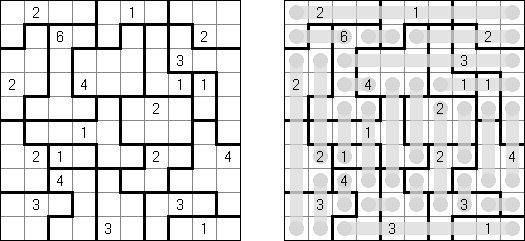
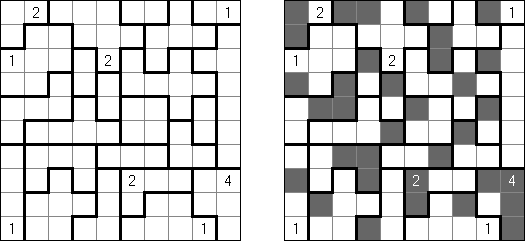
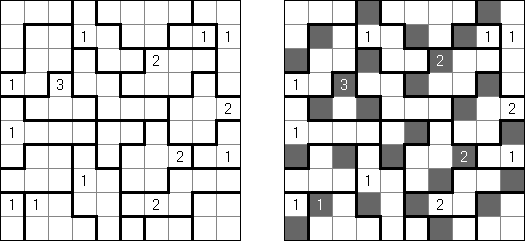
Battleships (전함 퍼즐, "Solitaire Battleships", "Battleship Solitaire")는 규칙이 유명한 전함 게임과 비슷한 퍼즐이다. 목적은 '전함'의 모서리도 서로 접촉하지 않도록 전함을 배치하는 것이다. 아래와 옆의 숫자는 전함의 부분이 본 행 또는 열에 몇 개가 들어 있는지를 뜻한다.

판의 표준 크기 - 10x10. 전부는 4칸 짜리 전함 1개, 3캍 짜리 점함 2개, 2칸 짜리 전함 3개 그리고 1칸 짜리 전함 4개가 있다. 전함의 일부가 이미 열려 있을 수 있다.

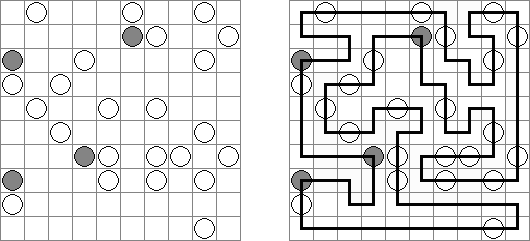
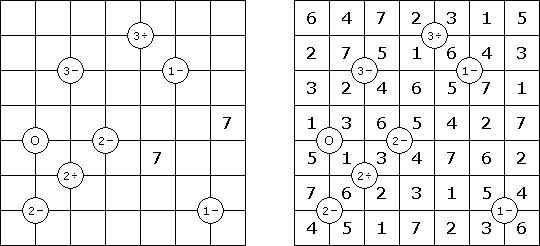
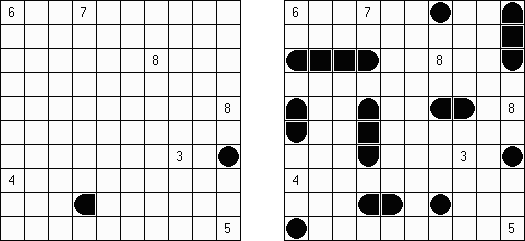
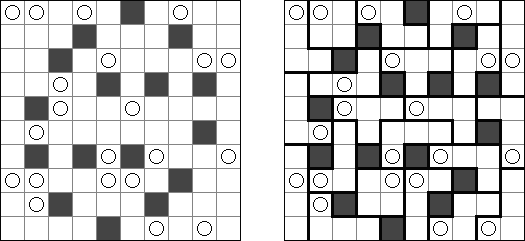
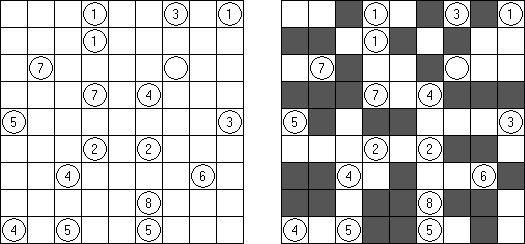
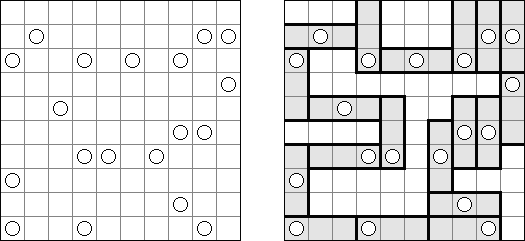
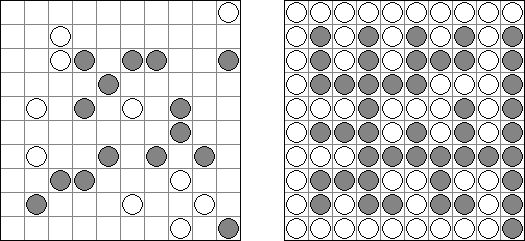
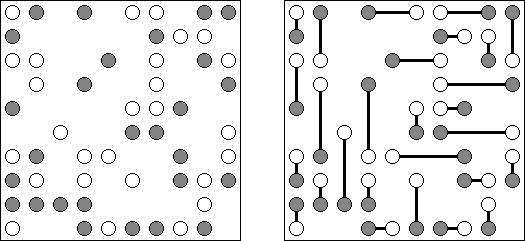
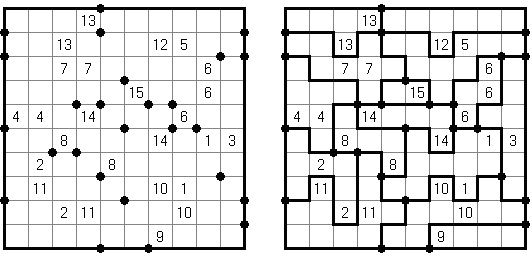
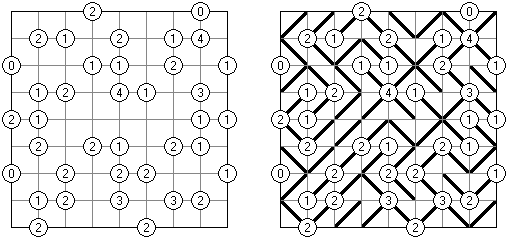
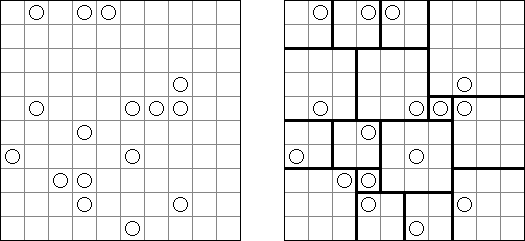
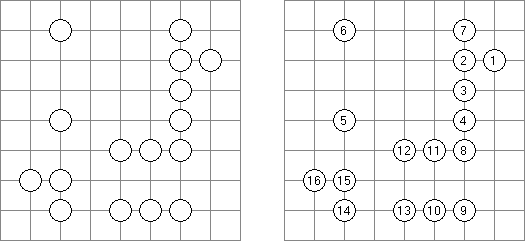
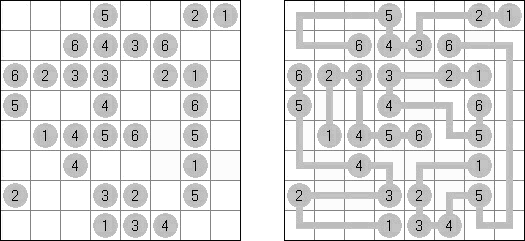
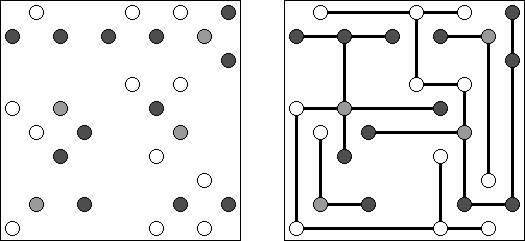
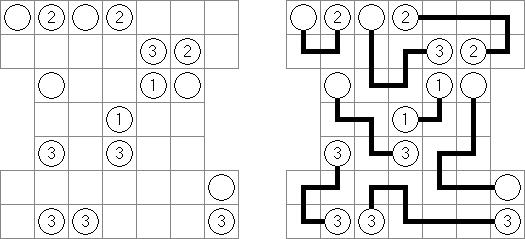
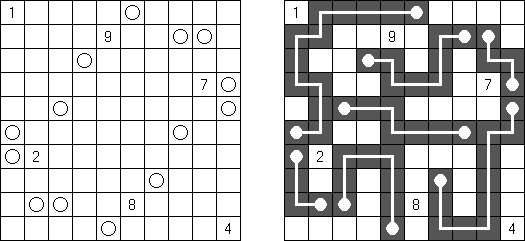
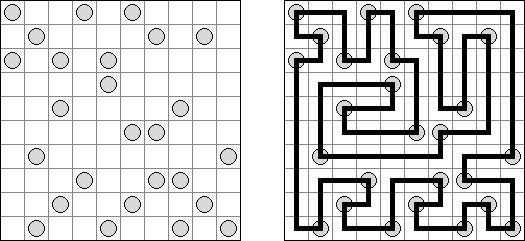
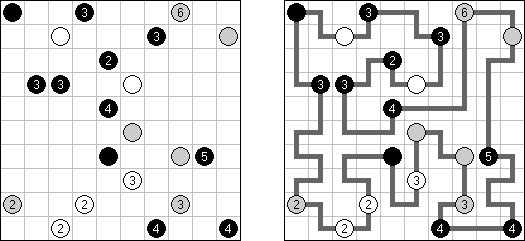
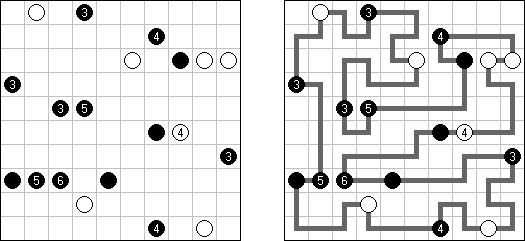
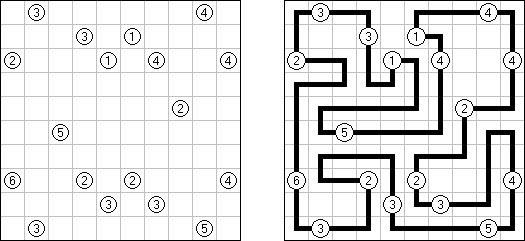
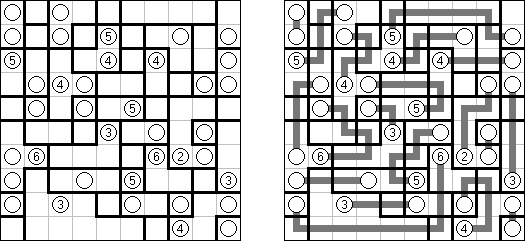
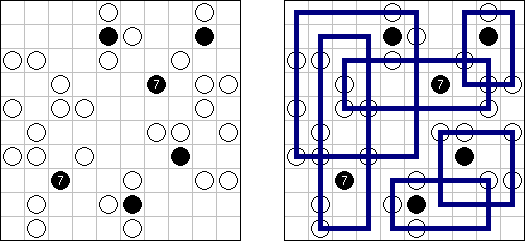
Hashiwokakero (교량 만들기, "Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai")는 숫자가 있는 동그라미('섬')를 직선('다리')로 연결해야 하는 퍼즐이다. 섬에 있는 숫자는 이 섬에 몇 개의 다리가 와야 하는지를 보여 준다. 고립된 섬이 있어서는 안 된다. 선은 모든 지은 다리를 통하여 모든 섬으로 갈 수 있도록 그려야 된다.

2개의 섬 가운데 2개 이상의 다리를 지으면 안 된다. 선은 가로세로 가면 되는데 대각선으로 가면 안 된다. 이 선이 편향-교차되거나 섬을 통과해서는 안 된다.

Masyu (마슈, "Shiroshinju Kuroshinju", "White Pearls and Black Pearls")는 자체를 교차하지 않는 하나의 폐쇄 회로가 되도록 흰 색과 검은 색 동그라미를 가로세로 직선으로 연결해야 하는 논리 퍼즐이다. 선은 흰 동그라미를 직선으로 통하는데 그전 또는 그후의 칸(아니면 그전 그후의 칸 둘 다)에서 방향을 변경해야 한다. 선이 검은 동그라미를 교차할 때 90도로 돌아야 한다. 이 때 그전이나 그후의 칸에서 방향을 변경해서는 안 된다.

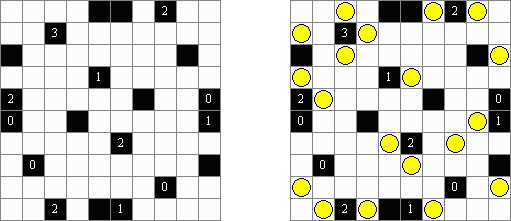
Akari (아카리, "Light Up", "Bijutsukan")는 논리 퍼즐이다. 판은 흰색과 검은 색 칸으로 되어 있고 어떤 검은 칸에 숫자가 있다. 판이 다 조명되도록 '등'을 흰 칸에 삽입해야 하는데 이 때 등이 서로에 빛을 내면 안 된다.

등불이 가로세로 확산하다가 검은 칸에 의해 차단될 수 있다. 검은 칸에 0부터 4까지의 숫자가 있을 수 있으며 이 숫자는 본 칸 옆에 등 몇 개(대각선으로 배치된 등 제외)가 배치되어야 하는지를 표시한다. 칸에 숫자가 없는 경우에 이 칸 옆에 등을 얼마든지 배치하면 된다.

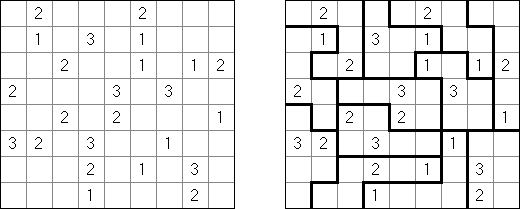
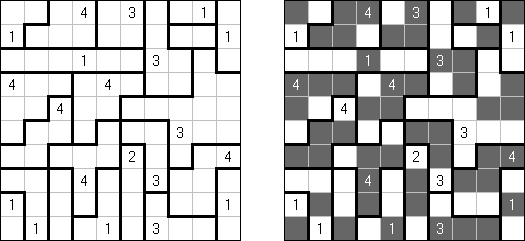
Fillomino (필로미노, "Polyominous")는 일정하지 않은 크기의 사각형 격자이며 일부 칸에 숫자가 있다. 목적은 판을 블록으로 나누는 것이다. 블록은 블록 칸의 숫자만큼의 칸을 포함해야 한다. 같은 크기의 블록이 가로세로 접촉해서는 안 된다. 처음에 숫자가 없었던 칸이 퍼즐 풀기에 필요한 블록으로 결합해서는 안 된다.

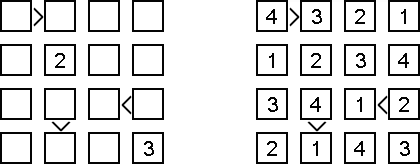
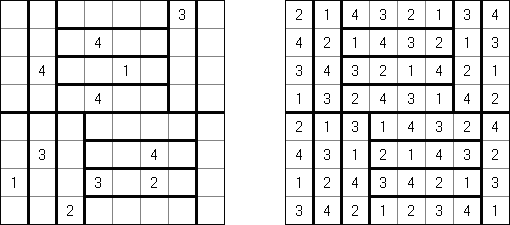
Futoshiki (후토시키, 불평등, "Hutoshiki", "Unequal")는 숫자 로직 퍼즐이다. 판이 사각형 격자이며, 일부 칸에 숫자가 있을 수 있으며, 칸 가운데 이웃 숫자 간의 관계를 보여주는 "<" 및 ">"기호가 포함될 수 있다. 퍼즐의 목적은 각 숫자가 각 행과 각 열에 한번만 들어 갈 수 있도록 빈 칸에 숫자를 넣는 것이다.

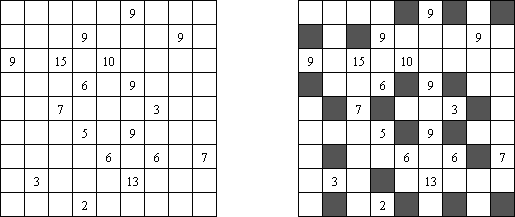
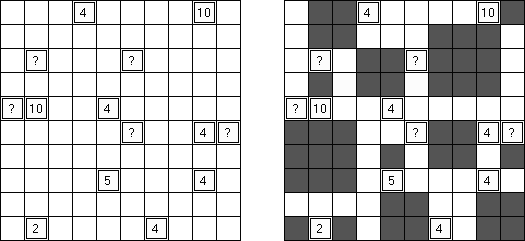
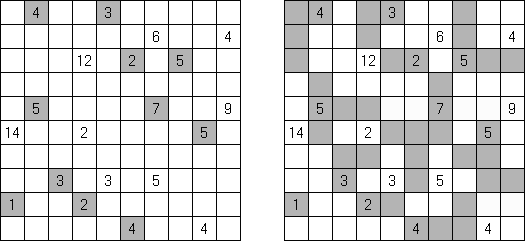
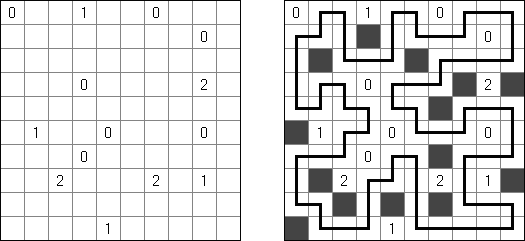
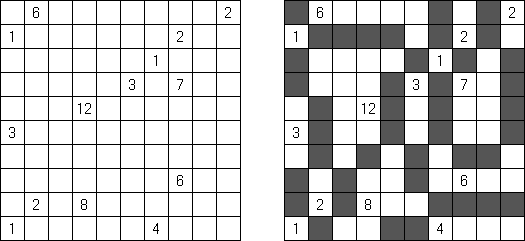
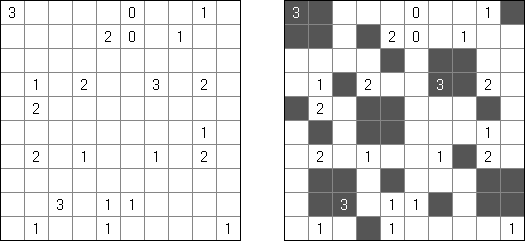
Kuromasu ("Kurodoko", "Where is Black Cells?")는 일부 칸에 숫자가 있을 수 있는 사각형 격자이다. 목적은 다음과 같은 조건에 따라 칸을 검은 색으로 색칠하는 것이다.

• 각 숫자는 본 칸에서 몇 개의 흰 칸이 가로세로 보이는지를 표시하며, 같은 행이나 열에 있는 두 개의 칸은 가운데 검은 칸이 없으면 서로를 볼 수 있다;
• 숫자가 있는 칸의 흰색이 변하지 않는다.
• 검은 칸은 가로세로 접촉할 수 없다.
• 모든 흰 칸이 하나의 공간을 구성하고 즉, 가로세고 접촉한다.

Nurikabe (누리카베, "Cell Structure", "Islands in the Stream")는 숫자 논리 퍼즐이다. 일본 신화에 '누리카베'란 통로를 차단하는 크고 안 보이는 벽의 형태로 된 괴물이다.

목적은 다음과 같은 규칙에 따라 섬의 위치를 보여주는 지도를 복원하는 것이다.

• 각 섬에 대한 정보는 이 섬이 몇 개의 칸을 사용하는지를 보여주는 숫자로 되어 있다.
• 각 두 개의 섬은 모서리로만 접촉할 수 있다.
• 각 섬에 대한 설명은 하나의 숫자를 포함한다.
• 섬 사이에 강이 있다.
• 강의 모든 칸이 서로 연결되어 있어야 한다.
• 지도는 모든 칸이 강을 포함한 2×2 네모가 하나라도 있어서는 안 된다.

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

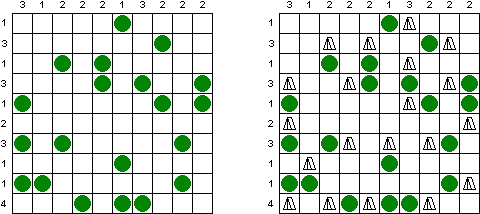
Tents (텐트퍼즐, "Tents and Trees")는 일부 칸이 '나무'를 포함하는 사각형 격자이다. 목적은 다음 규칙에 따라 나무 옆에 '텐트'를 배치하는 것이다.

• 텐트의 수는 나무의 수와 같다.
• 각 텐트는 '자기' 나무 옆에 가로세고 배치되고 대각선으로 배치돼서는 안 된다. 이 조건이 만족되면 '남'의 나무에 대한 위치는 상관 없다.
• 두 개의 텐트가 인접 칸(대각선으로 한 칸 포함)에 배치해서는 안 된다.
• 위와 옆의 숫자는 이 행이나 열에 몇 개의 텐트가 있는지를 표시한다.

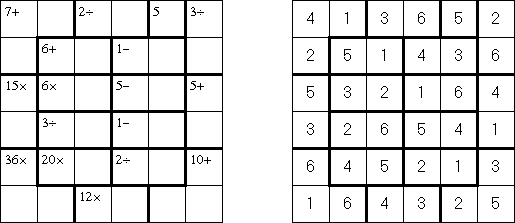
Calcudoku (캔캔, "KenKen", "KENKEN", "KenDoku", "Square Wisdom")은 수학적이고 논리적인 퍼즐이다. 목적은 숫자가 각 행과 각 열에 반복되지 않도록 이 숫자를 격자에 넣는 것이다. 굵은 선으로 둘러싼 각 블록(칸의 그룹)의 모서리에 있는 숫자는 이 블록의 숫자들에 대한 산술 연산의 결과이다. Killer Sudoku(킬러스도쿠)와 달리 블록 내부의 숫자는 반복될 수 있다.

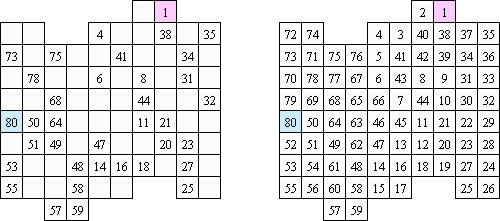
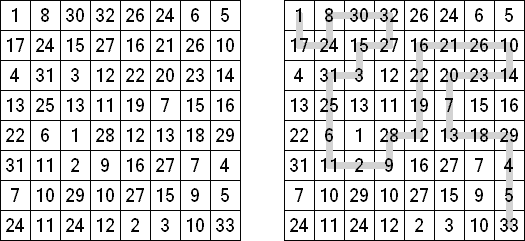
Hidato (히다토, 이디시어로: "나의 퍼즐"; 다른 명칭 - "Hidoku")는 이스라엘 수학자 기오라 베네덱(Gyora Benedek)이 발명한 퍼즐이다. 이 퍼즐은 일정하지 않은 형태(일반적으로 직사각형 또는 정사각형)의 칸으로 구성된 판이다. 목적은 퍼즐을 하는 자는 모든 칸을 가로, 세로 또는 대각선으로 연결된 연속적인 숫자로 채우는 것이다. 각 퍼즐은 이미 최소 및 최대 숫자가 있다. 또한 플레어가 퍼즐을 푸는 과정을 도와주고 과제 풀기가 하나 밖에 없도록 판에 다른 숫자도 있을 수 있다.

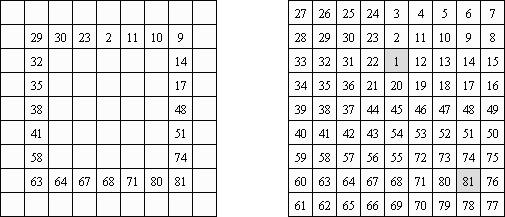
Numbrix는 논리 퍼즐의 일종이다. 이 퍼즐은 일부 칸에 숫자가 있는 직사각형 격자이다. 목적은 모든 숫자가 가로세로 연속적으로 연결되도록 빈 칸이 채우는 것이다. 대각선으로 이동해서는 안 된다.

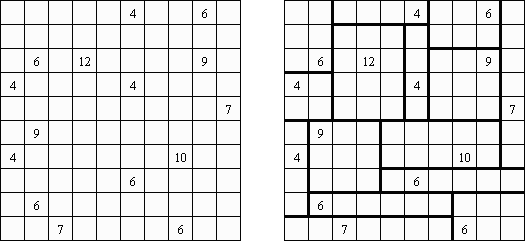
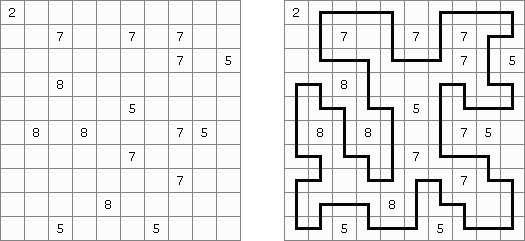
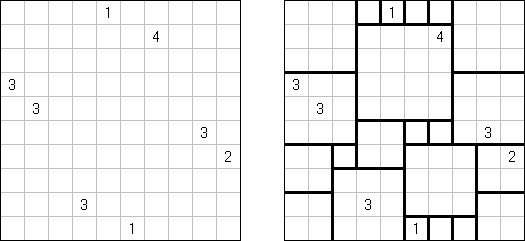
Shikaku (시카쿠, "Divide by Squares", "Divide by Box", "Number Area")는 논리 퍼즐이다. 이 퍼즐은 표준 크기가 없는 사각형 격자이다. 일부 칸에 숫자가 있다. 목적은 직사각형과 정사각형 지역으로 격자를 나누는 선을 그리는 것이다. 각 지역에 이 지역의 면적과 같은 숫자가 하나만 있어야 한다.

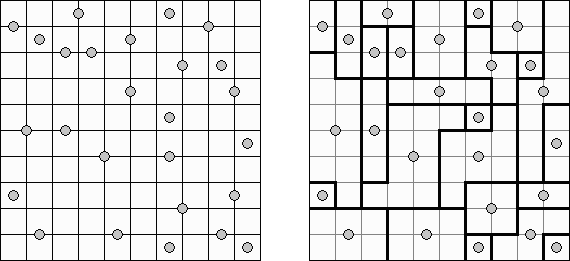
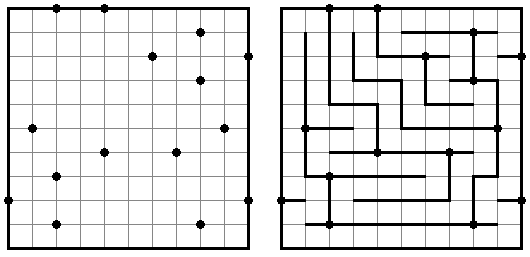
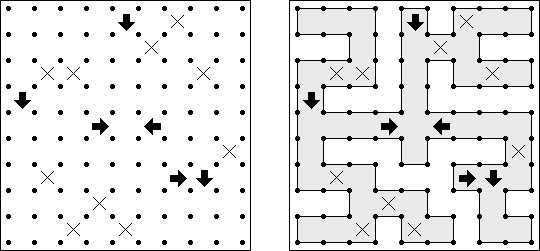
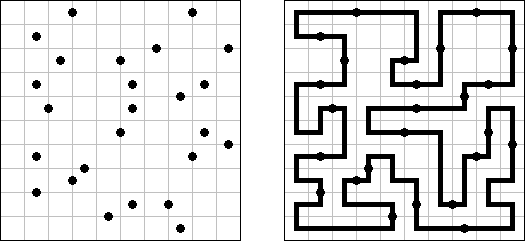
Galaxies (갤럭시, 은하, "Tentai Show")는 논리와 기하학을 결합한 퍼즐이다. 이 퍼즐은 점이 있는 사각형 격자이다. 목적은 격자를 지역으로 나누는 것이다. 각 지역은 점이 하나만 있어야 한다. 이 점은 본 지역에 있어서 대칭의 중심이다.

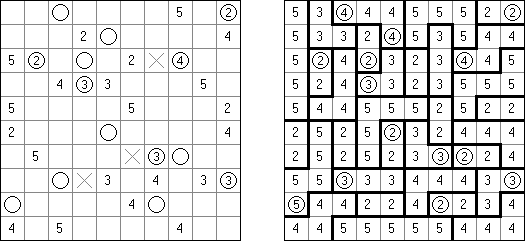
Skyscrapers (스키이스크래퍼, 마천루)는 논리 퍼즐의 일종이다. 목적은 각 숫자가 각 행과 각 열에 반복되지 않도록 이 숫자를 네모에 넣는 것이다. 판 내부의 각 칸에 칸의 숫자와 동등한 층의 수를 가지는 건물이 있고 판 외부의 숫자가 이 숫자에서 보면 해당 행 또는 열에 몇 개의 건물이 보이는지를 뜻한다고 생각하면서 각 칸을 숫자로 채워야 한다.

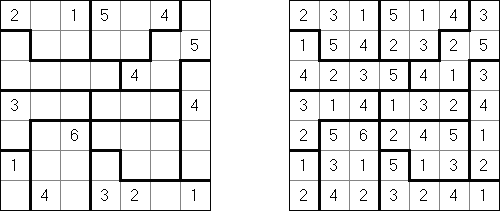
Hakyuu ("Ripple Effect", "Seismic")는 논리 퍼즐이다. 이 퍼즐은 블록(‘방’)으로 나뉘어진 사각형 격자이다. 일부 칸에 숫자가 있을 수 있다. 목적은 각 블록에 1부터 블록 칸의 수까지의 숫자가 있도록 모든 칸을 숫자로 채우는 것이다. 행이나 열에 같은 숫자 2개가 있으면 이 숫자 사이의 칸의 수는 본 숫자와 같거나 더 크다. 예를 들어, 열에 5을 가지는 칸 두 개 있는 경우에 이 칸 사이에 다른 숫자를 가지는 칸이 적어도 5개 있어야 한다.

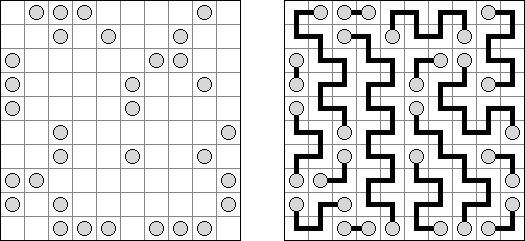
Grand Tour는 직사각형 또는 정사각형 격자의 모든 점을 통하여 자체와 접촉하거나 자체를 교차하지 않는 폐쇄 줄을 그려야 하는 논리 퍼즐이다. 과제 풀기가 하나 밖에 없도록 일부 점이 이미 줄로 연결되어 있다.

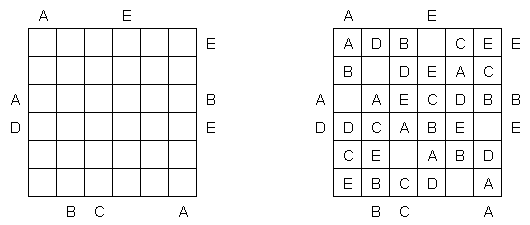
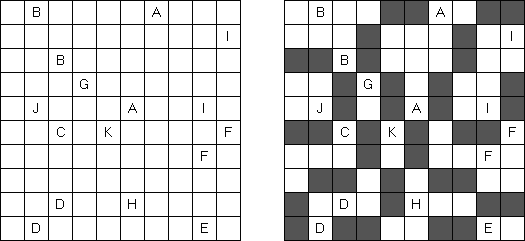
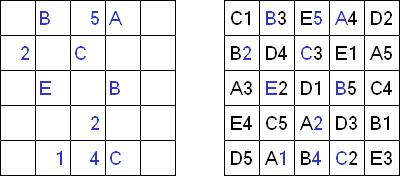
Easy as ABC ("ABC End View", "Last Man Standing")는 문자 논리 퍼즐이다. 이 퍼즐의 목적은 사각형 격자를 문자(예를 들어, A부터 E까지)로 채우는 것이다. 이 때 각 문자는 각 행 및 각 열에 한번만 나와야 한다. 일부 칸은 비어있을 수 있다. 격자 밖에 있는 문자는 본 행(열)에 어느 문자가 먼저 나오는지를 보여준다.

Clouds ("Radar")는 Battleships 퍼즐의 일종이다. 이 퍼즐의 목적은 일정하지 않은 형태 격자에 사각형(‘구름’)을 배치하는 것이다. 이 때 사각형의 모서리도 서로 접촉해서는 안 된다. 격자의 가장자리에 있는 숫자가 구름이 차지하는 칸의 수를 나타낸다. 구름의 수와 크기는 설정되어 있지 않다. 다만, 사각형 측면의 길이는 최소로 두 칸이다.

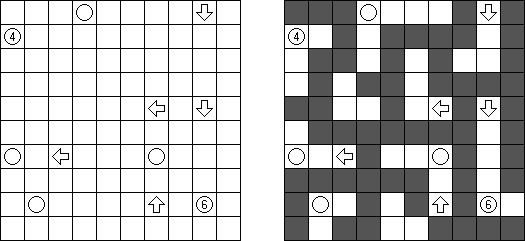
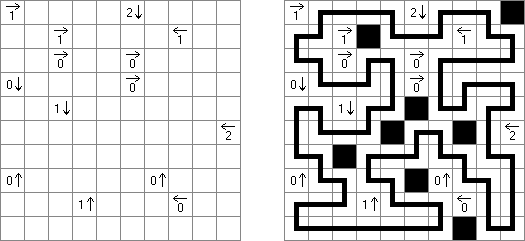
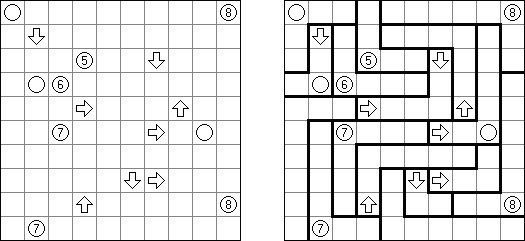
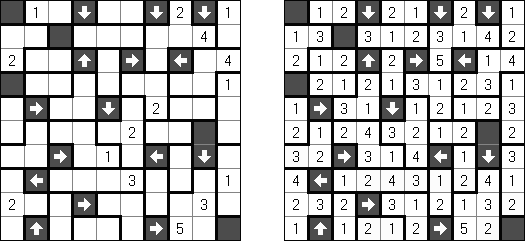
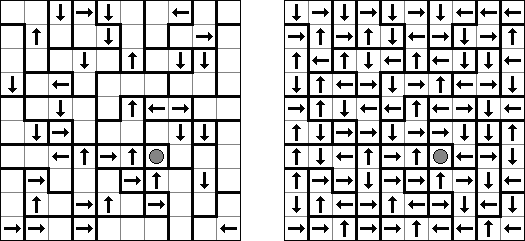
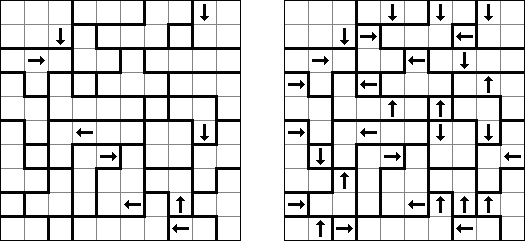
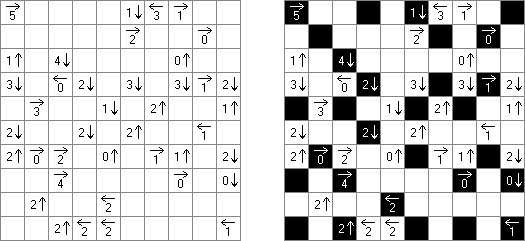
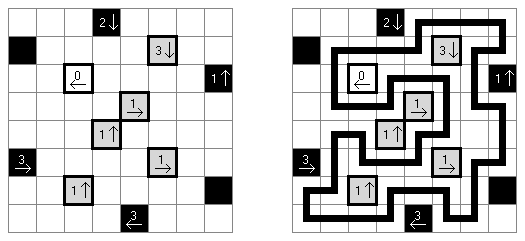
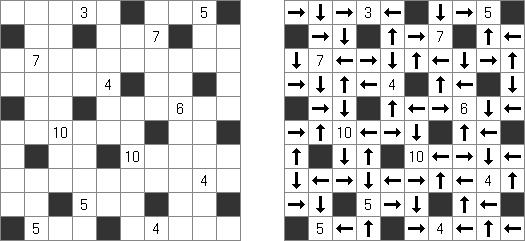
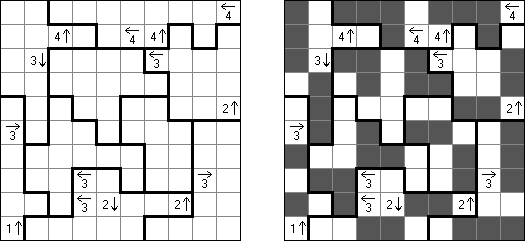
Yajilin ("Arrow Ring", "Straight and Arrow")은 정사각형 또는 직사각형 논리 퍼즐이다. 이 퍼즐은 화살표와 숫자를 포함한다. 이 정보는 판에 검은 칸을 배치할 때 필요하다. 이 퍼즐의 목적은 화살표가 있는 칸 또는 검은 칸을 통과하지 않고 자체를 교차하지 않는 폐쇄 고리(회로)를 그리는 것이다. The grid may contain gray cells that can not be part of the loop.

• 칸의 숫자는 화살표가 가리키는 행이나 열에 검은 칸 몇 개가 있는지를 보여준다. 화살표가 있는 칸 자체는 검은 칸으로 간주되지 않는다.
• 칸이 화살표도 없고 검지도 않은 경우에 이 칸은 고리(회로)의 부분을 포함해야 한다.
• 칸의 숫자는 검은 칸의 정확한 수를 나타낸다. 즉, 격자의 칸이 '3'과 왼쪽으로 가리키는 화살표가 있는 경우에 본 칸의 왼쪽에 검은 칸 3개가 있음을 뜻하는 것이다.
• 검은 칸은 가로세로 접촉해서는 안 된다.
• 판은 화살표가 가리키지 않는 검은 칸이 있을 수 있다.

Minesweeper (지뢰 찾기)는 Microsoft Windows 운영 체제의 사용자가 잘 안다. 목적은 숫자를 사용하면서 '지뢰'를 빈 칸에 넣는 것이다. 각 숫자는 이웃 칸 중에 지뢰가 있는 칸이 몇 개 있는지를 보여준다. 하나의 칸에 지뢰가 하나만 배치되고 숫자가 있는 칸에 지뢰가 있을 수 없다.

Minesweeper Battleships ("Battlemines")는 두 가지 유명한 퍼즐의 특징을 결합한다. 전함의 모서리도 서로 접촉하지 않도록 전함을 배치해야 한다. 격자의 일부 칸에 숫자가 있다. 이 숫자는 본 칸 주위(대각선 포함)에 전함의 부분 몇 개가 있는지를 보여준다.

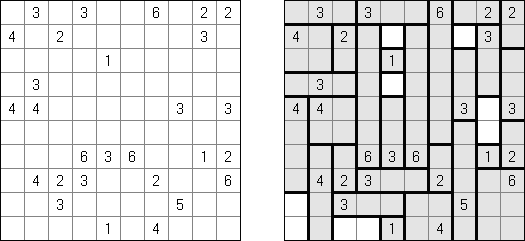
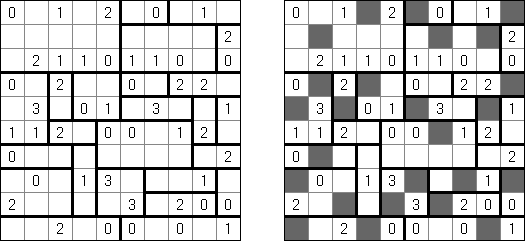
Heyawake (히토리)는 논리 퍼즐이다. 이 퍼즐은 블록('방')으로 나눠진 사각형 격자이다. 일부 블록은 숫자를 포함할 수 있다. 이 숫자는 각 블록에 검은 칸 몇 개가 있어야 하는지를 보여준다. 블록에 숫자가 없는 경우 이 블록은 아무 수의 검은 칸을 포함할 수 있다.

• 검은 칸이 대각선으로 접촉하면 되지만 가로세로 접촉해서는 안 된다.
• 모든 흰 칸은 가로 또는 세로 연결되어 있다.
• 흰 칸으로 된 연속 줄이 '방' 두 개 이상 교차해서는 안 된다.

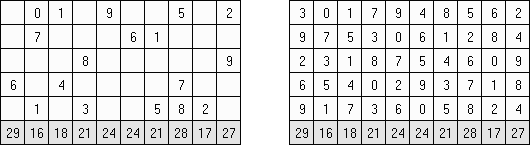
Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten")는 너비가 10 개의 칸으로 된 사각형 격자이다. 목적은 각 행이 0부터 9까지의 숫자를 포함하도록 격자를 채우는 것이다. 행의 숫자가 반복할 수 있다. 격자 아래의 숫자는 열에 있는 모든 숫자의 합계를 나타낸다. 인접 칸(대각선으로 접촉하는 칸 포함)의 숫자는 달라야 한다.

Hundred (백)는 각 칸에 숫자가 있는 정사각형 격자이다. 목적은 각 행과 각 열의 숫자 합계가 100이 되도록 추가 숫자를 넣는 것이다.

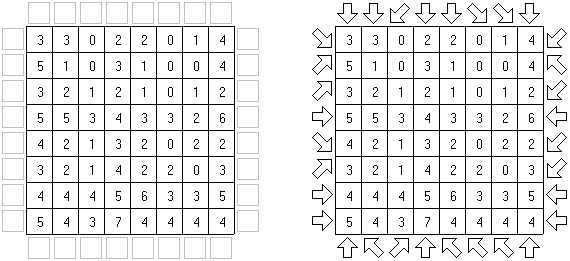
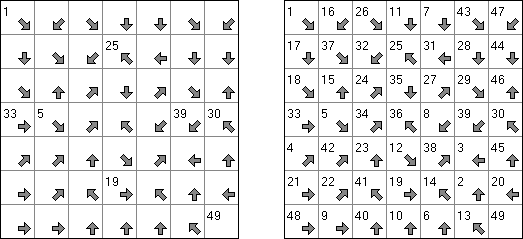
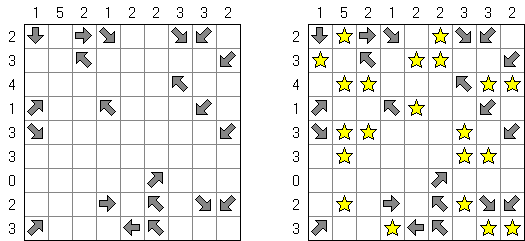
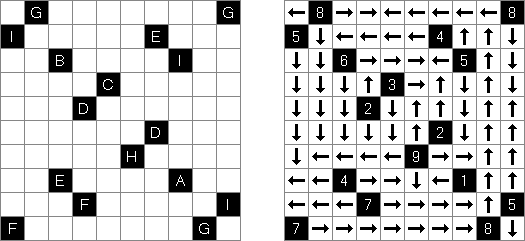
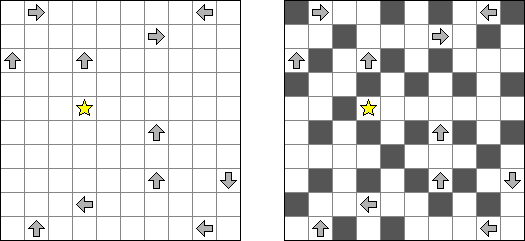
Arrows (화살)는 논리 퍼즐의 이종이다. 이 퍼즐은 숫자로 채워진 직사각형 또는 정사각형 격자이다. 퍼즐의 목적은 격자 외부에 화살표를 배치하는 것이다. 각 화살표는 숫자가 있는 칸 하나 이상을 가리킨다. 숫자는 본 칸을 가리키는 화살표의 수를 나타낸다.

Mathrax는 논리 퍼즐의 이종이다. 목적은 각 숫자가 각 행과 각 열에 반복되지 않도록 네모를 채우는 것이다. 숫자 중 일부는 이미 격자에 있을 수 있다. 격자 줄의 교차점에 다음과 같은 추가 조건을 가지는 동그라미가 있을 수 있다.

• 숫자 및 산술 연산의 기호 (덧셈, 뺄셈, 곱셈, 나눗셈) – 동그라미의 숫자는 이 동그라미에 인접하고 대각선으로 서로 접촉하는 칸의 숫자 쌍에 대한 산술 연산의 결과를 나타낸다.
• "E" 문자 - 동그라미에 인접한 칸들에 있는 4개의 숫자 모두 다 짝수이다. 여기에 "E"는 "even", "짝수"의 뜻이다.
• "O" 문자 - 동그라미 주위의 칸에 있는 4개의 숫자 다 홀수이다. 여기에 "O"는 "odd", "홀수"를 의미한다.

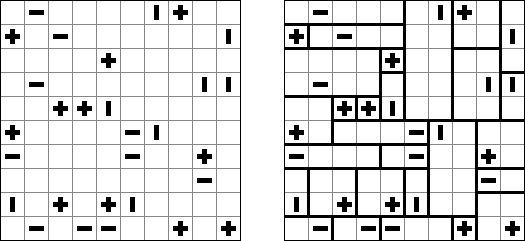
Str8ts ("Straights"; 포커 카드 게임에는 순서대로 5개의 카드를 의미한다)는 - 캐나다 사람 Jeff Widderich가 발명한 논리 퍼즐이다. 정사각형 격자는 흰 색과 검은 색 칸이 있다. 목적은 목적은 검은 칸 사이에 연속 숫자의 세트가 형성(오름차순인지 내림차순인지 상관 없음)되도록 흰 칸의 숫자를 배치하는 것이다. (예를 들어, 2-1-3-4). 각 행과 각 열에 있는 흰색 과 검은 색 칸의 숫자는 반복해서는 안 된다. 검은 칸의 숫자는 연속 숫자의 세트에 포함되지 않는다.

Linesweeper는 규칙이 Minesweeper 퍼즐과 비슷한 논리 퍼즐이다. 이 퍼즐은 정사각형이나 직사각형 격자이다. 격자의 일부 칸에 숫자(0에서 8까지)가 있다. 목적은 칸을 통하여 폐쇄 줄을 그리는 것이다. 줄이 자체를 교차하거나 숫자가 있는 칸을 통과해서는 안 된다. 칸의 숫자는 줄이 숫자가 있는 칸 주위에 배치된 칸 몇 개를 통과하는지를 보여준다.

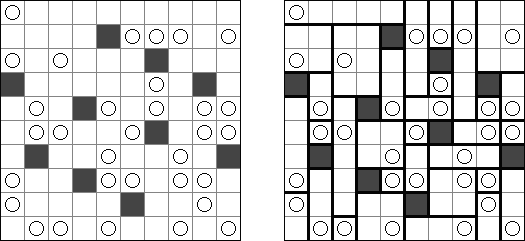
Binairo (이진 퍼즐, "Binary Puzzle", "Takuzu", "Tohu wa Vohu")는 0과 1을 사용하는 논리 퍼즐이다. 목적은 직사각형 또는 정사각형 격자를 다음과 같은 규칙에 따라 숫자로 채우는 것이다.

• 각 행과 각 열은 1과 0의 수가 같아야 한다. 홀수 크기의 격자 경우에 둘 중에 하나 더 많은 것이다.
• 같은 숫자는 연속으로 2개 이상의 칸에 있어서는 안 된다.
• 각 행과 각 열은 유일해야 한다.

Walls는 일본 사람 나오키 이나바(Naoki Inaba)가 발명한 논리 퍼즐이다. 목적은 검은 칸에서 나오는 모든 ‘광선’의 총 길이가 이 칸의 숫자와 일치하도록 흰 칸에 수평과 수직 줄을 삽입하는 것이다.

Dominosa (도미노사, "Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt")는 도미노 패가 사용되는 논리 퍼즐이다. 판에 숫자만 표시되어 있다. 목적은 도미노 패 사이의 경계를 복원하는 것이다.

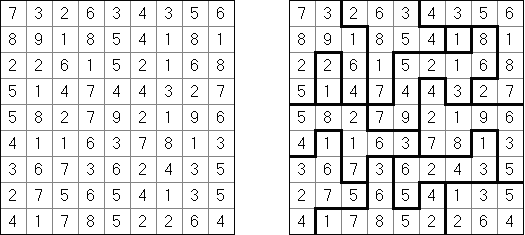
Patchwork (패치워크, "Tatami")는 같은 크기의 지역('방')으로 나뉘어진 정사각형 격자인 퍼즐이다. 목적은 1부터 지역 칸의 수와 같은 숫자까지의 숫자로 각 방을 채우는 것이다. 각 행과 각 열은 각 숫자 종류의 같은 수를 포함해야 한다. 가로세로 접촉하는 이웃 칸은 같은 숫자를 포함해서는 안 된다.

이 종류 퍼즐의 일부 과제는 숫자 대신에 문자가 사용된다. Cross+A은 숫자 퍼즐만 아니라 문자 퍼즐도 풀 수 있다.

Knossos (크노소스 – 크레타 섬에 있는 고대 도시와 궁전 또한 미노타우로스가 투옥되었던 미로의 소재지)는 일부 칸에 숫자가 있는 직사각형 또는 정사각형 격자이다. 목적은 각 지역에 숫자 하나만 있도록 격자를 지역('방')으로 나누는 것이다. 이 숫자는 지역의 경계의 길이와 같아야 한다.

Rekuto는 정사각형 또는 직사각형 논리 퍼즐이다. 격자의 일부 칸에 숫자가 있다. 목적은 직사각형과 정사각형 지역으로 격자를 나누는 줄을 그리는 것이다. 각 지역에 이 지역의 너비 맟 높이의 합계와 동등한 숫자가 하나만 있어야 한다.

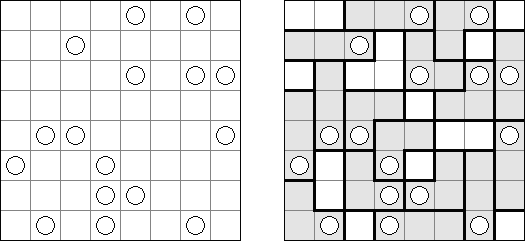
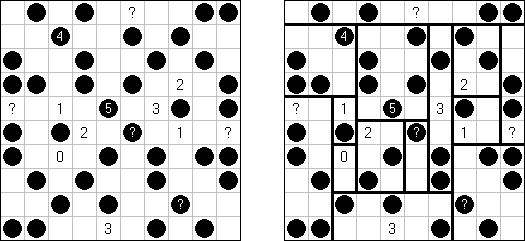
Neighbours (이웃들)는 일정하지 않은 형태의 격자인 논리 퍼즐이다. 격자의 일부 칸에 숫자 또는 물음표가 있다. 목적은 격자를 칸의 수가 같은 지역으로 나누는 것이다. 각 지역은 숫자가 있는 칸(또는 물음표)이 하나만 있어야 한다. 이 숫자는 본 지역이 '이웃'이 몇 개 있어야 하는지를 보여준다. 두 지역이 공통의 경계가 있는 경우 이웃 지역으로 간주된다. 물음표를 포함하는 지역은 '이웃'이 얼마든지 있을 수 있다.

Four Winds (네 바람, "Line Game")는 검은 색과 흰 색 칸이 있는 정사각형 또는 직사각형 격자인 논리 퍼즐이다. 목적은 검은 칸에서 나와서 모든 흰 칸을 통과하는 직선을 그리는 것이다. 검은 칸의 숫자는 이 검은 칸과 연결된 줄이 몇 개의 흰 칸은 배치하는지를 보여준다. 줄이 서로 교차해서는 안 된다.

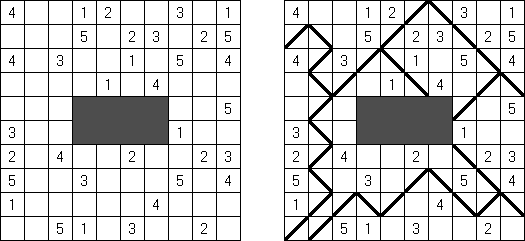
Shakashaka (샤카샤카, "Proof of Quilt")는 정사각형 또는 직사각형 논리 퍼즐이다. 퍼즐은 흰 색과 검은 색 칸으로 되어 있다. 일부 검은 칸에 숫자(0에서 4까지)가 있을 수 있다. 목적은 직사각형과 정사각형 흰 지역이 생기도록 검은 세모를 흰 칸에 넣는 것이다. 일부 흰 칸이 비어 있을 수 있다. 지역은 가로세로 또는 대각선 방향으로 배치될 수 있다. 흰색 이웃 지역은 공통의 측면이 있어서는 안 된다. 검은 칸의 숫자는 이 칸과 접촉하는 세모 몇 개 있는지를 보여준다.

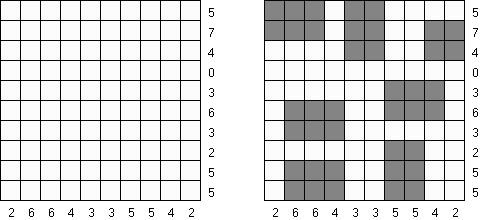
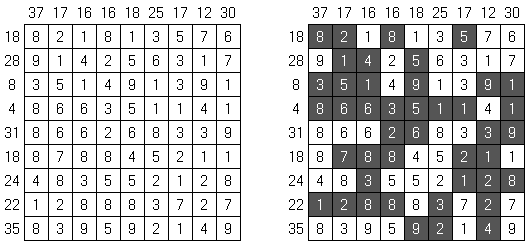
Kakurasu ("Index Sums")는 검은 색과 흰 색 칸을 정리해야 하는 정사각형 또는 직사각형 퍼즐이다. 격자의 왼쪽과 위에 있는 숫자는 행과 열에 있는 검은 칸 '무게'의 합계를 나타낸다. 격자의 오른쪽과 아래에 있는 숫자는 해당 행과 열에 있는 검은 칸 '무게'를 정한다. 첫 행 또는 첫 열에 있는 검은 칸의 '무게' - 1, 둘째 행 또는 둘째 열에 - 2 등.

Mochikoro ("Mochinuri")는 일부 칸에 숫자가 있는 직사각형 또는 정사각형 격자이다. 목적은 흰 칸으로 된 직사각형 또는 정사각형 '섬'이 생기도록 검은 칸과 흰 칸을 배치하는 것이다.

• 한 개의 '섬'이 숫자가 있는 칸 한 개 이상 포함해서는 안 된다.
• 일부 '섬'은 숫자가 있는 칸을 포함 안 한다.
• 흰색 지역이 측면으로 접촉해서는 안 되지만 모든 흰 '섬'은 대각선으로 서로 접촉한다.
• 격자에 검은 칸으로만 구성된 2×2 네모가 하나라도 있어서는 안 된다.

Seethrough (문들, "Doors", "Open Office")는 각 칸이 '방'을 의미하는 정사각형 또는 직사각형 논리 퍼즐이다. 목적은 방 사이의 '문'을 열거나 닫는 것이다. 열린 방은 한 방에서 다른 방으로 또는 여러 방을 통해 보기를 가능하게 한다. 숫자는 본 방에서 본 방을 제외하고 몇 개의 방이 보이는지를 나타낸다. 서로 격리된 격자의 부분이 있으면 안 된다. 즉, 어느 방에서든지 어느 방에든지 갈 수 있다.

Lighthouses (등대)는 숫자('등대')가 있는 검은 칸을 포함하는 논리 퍼즐이다. 숫자는 본 등대가 조명하는 선박의 수를 나타낸다. 등대와 선박의 사이에 다른 선박이나 등대가 있는 경우에도 같은 행이나 열에 배치되어 있으면 등대는 선박을 조명한다. 각 선박은 적어도 한 개의 등대에 의해 조명된다. 선박은 서로 또는 등대와 접촉(대각선 포함)해서는 안 된다.

Lighthouse Battleships (등대 전함)은 Battleships (전함)과 Lighthouses (등대) 퍼즐을 결합한 것이다. 숫자가 있는 칸은 등대이고, 이 숫자는 등대와 같은 열 또는 행에 있는 선박 조각의 전체 갯수를 의미한다. 선박은 대각선으로도 등대에 접촉할 수 없다.

Tapa는 터키인 세르칸 유레클리(Serkan Yürekli)가 발명한 퍼즐이다. 이 퍼즐은 흰 칸으로 구성된 정사각형 또는 직사각형 격자이다. 목적은 다음과 같은 규칙에 따라 일부 칸을 검은 색으로 색칠하는 것이다.

• 모든 검은 칸이 가로 또는 세로 접촉해야 한다.
• 검은 칸으로만 구성된 2×2 칸의 그룹이 있어서는 안 된다.
• 일부 칸이 숫자나 물음표를 포함한다. 이러한 칸은 항상 흰색이다.
• 각 숫자는 이 숫자를 포함하는 흰 칸 주위에 있는 검은 칸의 연속적인 그룹을 나타낸다. 검은 칸의 그룹 두 개 사이에 적어도 흰 칸 한 개가 있어야 한다.
• 물음표는 0보다 큰 숫자를 의미한다.
• 숫자의 위치 또는 숫자의 배치 순서는 상관 없다.

Fobidoshi ("Forbidden Four")는 일본인 나오키 이나바(Naoki Inaba)가 발명한 퍼즐이다. 이 퍼즐은 일부 칸에 동그라미가 있는 직사각형 또는 정사각형 격자이다. 목적은 모든 동그라미가 가로 또는 세로 접촉하도록 이 동그라미를 빈 칸에 넣는 것이다. 수평 또는 수적으로 연속 4 동그라미가 있어서는 안 된다.

Island (섬, "Tents Island", "Airando")는 일본인 나오키 이나바(Naoki Inaba)가 발명한 퍼즐이다. 이 퍼즐은 일부 칸에 숫자가 있는 격자이다. 목적은 남은 흰 칸이 한 섬을 형성하도록 칸을 검은 색으로 색칠하는 것이다. 숫자가 있는 칸이 섬의 일부이다. 숫자는 숫자가 있는 칸으로부터 가로세고 가(숫자가 있는 다른 칸이 길을 차단할 때까지)면 숫자가 없는 흰 칸 몇 개를 달성할 수 있는지를 나타낸다.

Dominion (도미니온)은 일부 칸에 문자가 있는 격자이다. 목적은 다음과 같은 규칙에 따라 일부 칸을 검은 색으로 색칠하는 것이다.

• 검은 칸은 2개씩만 판에 추가할 수 있다. 즉, 각 2개의 검은 칸은 가로 또는 세로 접촉해야 한다. 이러한 칸 쌍은 '도미노 패'라고 한다.
• 도미노 패는 대각선으로만 접촉할 수 있다.
• 문자가 있는 칸의 흰 색이 변해서는 안 된다.
• 검은 칸은 판을 별도의 흰 지역으로 나눈다. 한 지역 내부의 모든 흰 칸은 가로 또는 세로 접촉한다.
• 같은 문자를 가지는 칸들이 같은 흰 지역에 속한다.
• 문자를 포함하는 칸이 없는 흰 지역이 있을 수 없다.

Tren (트렌)은 일본인 시니치 아오키(Shinichi Aoki)가 발명한 논리 퍼즐이다. 이 퍼즐의 명칭은 일본말로 '주차장'이라고 의미한다. 각 블록은 자동차이고 전체 격자는 주차장이다. 이 퍼즐은 일부 칸에 숫자가 있는 직사각형 또는 정사각형 격자이다. 목적은 1×2 또는 1×3 크기의 블록을 격자에 배치하는 것이다. 각 숫자는 한 블록의 일부가 되어야 한다. 이 숫자는 몇 개의 칸만큼 블록을 이동할 수 있는지를 나타낸다. 블록은 이것의 짧은 측면 방향으로만 이동할 수 있다.

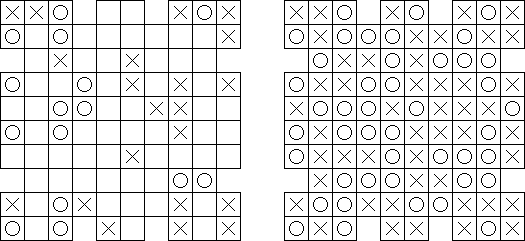
No Four in a Row 는 불규칙한 모양의 격자에서 하는 게임이다. 격자의 일부에는 'X'와 'O'가 있다. 목적은 가로, 세로 또는 대각선으로 연속 네 개의 동일한 부호가 나타나지 않도록 격자를 채우는 것이다.

Corral (울타리, "Bag", "Cave") 은 니콜리(Nikoli)가 개발한 논리 퍼즐이다. 목적은 격자 선을 따라 교차하지 않는 하나의 닫힌 고리를 그리는 것이다. 이 고리는 모든 숫자 주위를 돈다. 격자 안의 숫자는 해당 칸에서 가로 및 세로로 그 칸을 포함하여 몇 개의 칸이 보이는 지를 의미한다. 단서 숫자를 대신해서 물음표를 사용할 수 있다. 각각의 물음표는 0이 아닌 정수를 나타낼 수 있다.

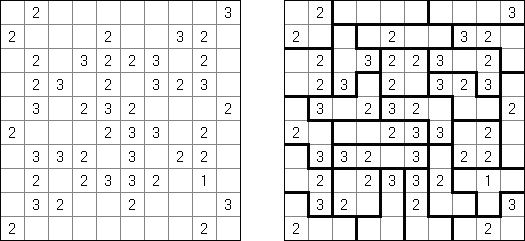
Foseruzu ("Four Cells")은 니콜리(Nikoli)가 발표한 일종의 논리 퍼즐이다. 목적은 격자를 정확히 네 칸으로 구성된 지역으로 나누는 것이다. 각 칸에 있는 숫자는 해당 칸의 네 측면 중 몇 개가 지역 경계선의 일부가 되는지를 나타낸다(격자 가장자리 포함).

Faibuseruzu ("Five Cells", "Solomon's Keep"): 격자를 정확하게 다섯 칸으로 구성된 지역으로 나누어야 한다.

Sutoreto ("Sutoretokurosu", "Straight Cross") 는 일본인 나오키 이나바(Naoki Inaba)가 만든 논리 퍼즐이다. 이 게임은 검은 색과 흰 색의 칸이 있는 직사각형 또는 정사각형 격자에서 한다. 일부 흰 칸에는 숫자가 있다. 목적은 모든 흰 칸에 숫자를 배치하는 것이다. 가로 또는 세로로 연이어져 있는 흰 칸은 순서는 상관없지만, 간격이 없는 연속적인 숫자의 배열을 만들어야 한다(예를 들어, 2-4-1-3).

Renban 은 지역으로 나뉘어진 정사각형 격자로 구성되어 있다. 목적은 각 칸을1에서 N 사이의 숫자로 채우는 것인데, 여기서 N은 퍼즐 측면의 크기이다. 한 행, 열, 또는 지역에 한 숫자가 두 번 이상 나타나서는 안된다. 한 지역에 있는 모든 숫자는 순서는 상관없지만, 연속적인 숫자의 배열을 만들어야 한다 (예를 들어, 5-3-4).

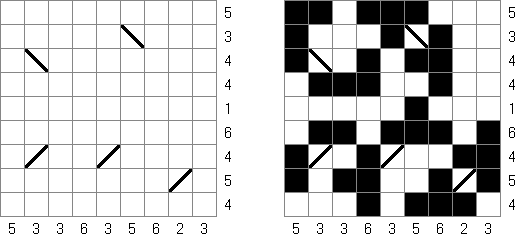
Buraitoraito ("Bright Light")은 직사각경 또는 정삭각형 격자에서 한다. 격자는 숫자가 있는 검은 칸을 포함한다. 각 칸의 숫자는 해당 칸에서 몇 개의 별표를 볼 수 있는 지를 나타낸다. 별표는 해당 칸과 같은 행이나 열에 있으면 검은 칸에서 볼 수 있지만, 다른 검은 칸 뒤에 있는 것은 볼 수 없다.

Irasuto (일러스트레이션, "Illustration")은 일본인 나오키 이나바(Naoki Inaba)가 만든 논리 퍼즐이다. 직사각형 또는 정사각형 격자는 숫자가 있는 검은 색과 흰 색의 칸을 포함한다. 목적은 다음과 같은 규칙에 따라 격자의 일부 칸을 검은 색으로 칠하는 것이다:

• 흰 칸의 숫자는 해당 칸에서 보이는 비어있는 흰 칸의 갯수를 나타낸다.
• 검은 칸의 숫자는 해당 칸에서 보이는 비어있는 검은 칸의 갯수를 나타낸다.

Suguru (숫자 블록, "Number Blocks")은 일본인 나오키 이나바(Naoki Inaba)가 발명한 논리 퍼즐이다. 이 게임은 지역으로 나누어진 직사각형 또는 정사각형 격자로 구성되어 있다. 각 지역을 1에서 해당 지역의 칸 갯수 사이의 숫자로 채워야 한다. 동일한 숫자를 가진 칸이 가로나 세로 또는 대각선으로 인접해 있어서는 안된다.

Trinudo 는 논리 퍼즐이다. 이 게임은 직사각형 격자에서 한다. 격자의 일부 칸은 “정해진 수(givens)”라고 불리는 숫자들을 포함한 채로 시작한다. 목적은 격자를 하나, 둘 또는 세 칸으로 구성된 블록으로 나누는 것이다. 동일한 크기의 블록이 가로나 세로로 인접해 있어서는 안된다. 각각의 주어진 숫자는 그 숫자가 포함된 블록의 크기를 나타낸다.

Creek (개울, "Kuriku") 는 직사각형 또는 정사각형 격자에서 하는 게임이다. 0에서 4까지의 숫자가 있는 원이 격자 내부 선들의 교차지점에 위치할 수 있다. 이 원 안에 있는 숫자는 인접해 있는 칸 중 몇 개를 검은 색으로 칠해야 하는 지를 보여준다. 전체 흰 칸이 가로 또는 세로로 연결되어야 한다.

Gappy (토막토막)는 정사각형 격자에서 하는 게임이다. 목적은 다음과 같은 규칙에 따라 격자의 일부 칸을 검은 색으로 칠하는 것이다:

• 각 행과 열에는 두개의 검은 칸이 있다.
• 어떤 검은 칸도 대각선으로도 서로 접촉해서는 안된다.
• 격자 외부의 숫자는 해당 행 또는 열의 검은 칸 사이에 있는 흰 칸의 갯수를 의미한다.

Norinori 는 니콜리가 만든 논리 퍼즐이다. 직사각형 또는 정사각형의 격자가 구간으로 나뉘어져 있다. 목표는 다음의 규칙에 따라 격자의 일부 칸을 검게 칠하는 것이다:

• 각 구간은 정확히 두 개의 검은 칸을 포함한다.
• 각 검은 칸은 구각의 경계와 상관없이, 2×1 또는 1×2 블록 (도미노)의 일부이어야 한다.
• 두 도미노는 모서리를 공유할 수 없다. 검은 색 블록은 서로 대각선으로 접할 수 있다.

Yonmasu ("Yonmasubunkatsu") 는 일본인 나오키 이나바(Naoki Inaba)가 발명한 논리 퍼즐이다. 직사각형 또는 정사각형 격자의 일부 칸에는 원이 있다. 목적은 이 격자를 정확히 네 개의 칸으로 구성된 지역으로 나누는 것이다. 각 지역은 하나의 원을 포함한다.

Bricks (벽돌 게임)는 정사각형 격자로 되어 있다. 이 게임의 목적은 각 칸을 1에서 N(퍼즐 한 면의 크기)까지의 숫자로 채우는 것이다. 한 행이나 열에 같은 숫자가 두 번 나타날 수 없다. 각 벽돌에는 짝수와 홀수가 다 있다.

Number Chain (숫자 사슬)은 Leonid Mochalov (러시아)가 만든 논리 퍼즐이다. 직사각형이나 정사각형 격자의 각 칸에 1에서 N까지의 숫자가 있다. 게임의 목적은 왼쪽 위 모서리에서 오른쪽 아래 모서리까지 한 줄의 실선을 그리는 것이다. 이 선은 1에서 N까지의 각 숫자를 정확하게 한 번씩 포함한다.

Kapetto (카펫 깔기, "Settokapetto", "Set Carpets") 는 나오키 이나바(일본)가 발명한 논리 퍼즐이다. 이 퍼즐은 직사각형이나 정사각형 격자에서 한다. 일부 칸 안에는 숫자가 있다. 퍼즐의 목표는 각 블록이 정확히 하나의 숫자만 포함하도록 격자를 직사각형 모양의 블록으로 나누는 것이다. 이 숫자는 블록 내에 있는 칸의 갯수를 나타낸다. 격자는 어떤 블록에도 포함되지 않는 칸을 가질 수 있다.

Renkatsu 는 일본인 나오키 이나바(Naoki Inaba)가 만든 논리 퍼즐이다. 이 게임은 숫자들로 채워진 직사각형 또는 정사각형 격자에서 한다. 이 격자를 지역으로 나누어야 한다. 각 지역은 1에서 해당 지역의 칸 갯수까지의 숫자를 포함한다.

Eulero (그레코 라틴 방진, "Graeco-Latin Square", "Euler Square") 는 문자와 숫자가 있는 퍼즐이다. 목적은 다음의 규칙에 따라 격자를 기호를 채우는 것이다:

• 각 칸은 하나의 문자와 한 자리 숫자를 포함한다.
• 모든 열과 행은 각각의 문자와 숫자를 정확하게 한 번씩만 포함한다.
• 어떤 두 칸도 동일한 기호쌍을 포함할 수 없다.

Anraikumozaiku (서로 다른 모자이크, "Unlike Mosaic")는 나오키 이나바(Naoki Inaba, 일본)가 만든 논리 퍼즐이다. 직사각형이나 정사각형 격자의 일부 칸에 동그라미가 있다. 목적은 격자를 직사각형 구역으로 나누는 것이다. 각 구역은 하나의 동그라미를 가지고 있다. 검은 칸은 어떤 구역에도 포함되지 않는다. 동일한 크기의 구역은 모서리를 공유할 수 없다.

Kurotto (일본어에서, 문자 그대로 검은색 단위)는 니콜리(Nikoli)가 발표한 논리 퍼즐이다. 이 게임은 일부 칸에 동그라미가 있는 격자로 되어 있다. 동그라미는 그 안에 숫자가 있을 수도 없을 수도 있다. 게임의 목적은 다음의 규칙에 따라 격자의 일부 칸을 검은 색으로 색칠하는 것이다:

• 동그라미가 있는 칸은 검은 색으로 칠할 수 없다.
• 검은 칸은 직각으로 이어진 영역을 형성한다.
• 동그라미 안의 숫자는 동그라미가 있는 칸과 직각으로 인접해있는 영역의 검은 색 칸의 갯수를 나타낸다.
• 비어있는 동그라미를 가진 칸은 그 주위에 몇 개의 검은 색 칸이 있든지 상관없다.

Tasukuea (from Japanese, literally "find squares") is a type of logic puzzles. It is played on a rectangular or square grid with numbers or question signs in some cells. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers or question signs can not be blacken.
• Black cells form square areas, that must not be orthogonally adjacent.
• A number in a circle indicates the total number of black cells in areas orthogonally neighboring the numbered cell.
• A cell with a question sign must have at least one adjacent black cell.
• All the white cells must be connected horizontally or vertically.

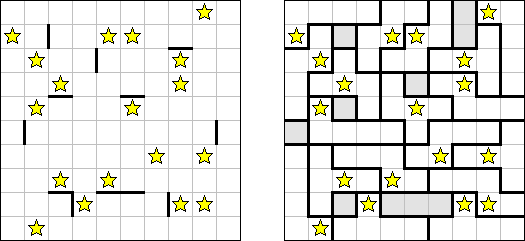
Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.

Araf (from Turkish, literally "purgatory"; original Japanese name - "Aidabeya") is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.

Kabingurodo (커브 길, "Curving Road") 는 나오키 이나바(일본)가 발명한 논리 퍼즐이다. 이 퍼즐은 일부 칸에 동그라미가 있는 격자로 되어 있다. 목표는 다음의 규칙에 따라 격자의 일부 칸을 검게 칠하는 것이다:

• 동그라미가 있는 칸은 항상 흰색이어야 한다.
• 검은 칸은 직각으로 연결되어서는 안된다.
• 모든 흰색 칸은 직각으로 연결된 구역을 형성해야 한다.
• 한 동그라미에서 다른 동그라미로 가는 흰색 칸으로 된 길은 적어도 두번은 방향을 바꾸어야 한다.

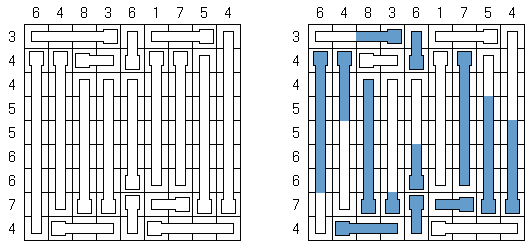
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.

Snake ("Tunnel") is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.

Peintoeria ("Paint Area") is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All cells of a region must have the same color.
• A cell with a number indicates how many black cells are adjacent to it.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the same color.

Irupu ("I-Loop") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.

Sashigane (from Japanese, literally "carpenter's square") is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.

Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

Chocona ("Chocolate") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any number of cells may be blackened.
• The black cells must form rectangles, independently of the region borders.
• The black rectangles must not be orthogonally adjacent.

Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.

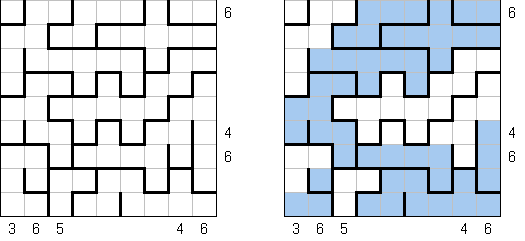
LITS ("Nuruomino") is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.

The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.

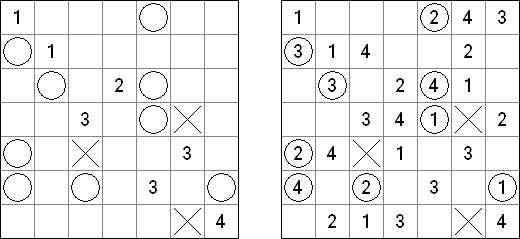
Nanbaboru ("Number Ball") consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.

Tairupeinto ("Tile Paint", "Crazy Pavement") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.

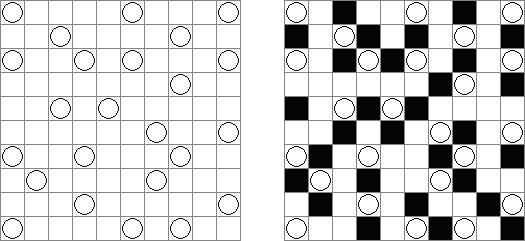
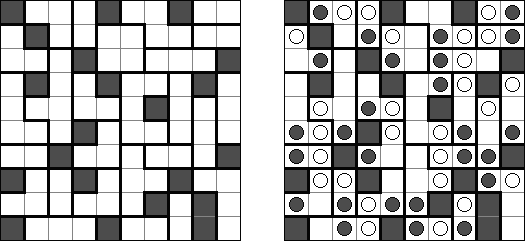
Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.

Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.

Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.

Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.

Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.

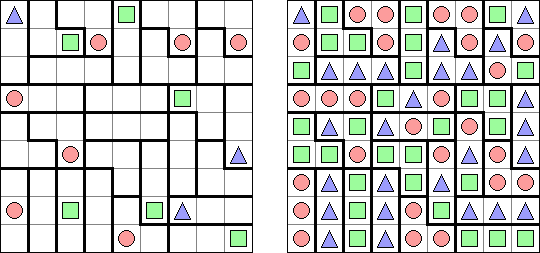
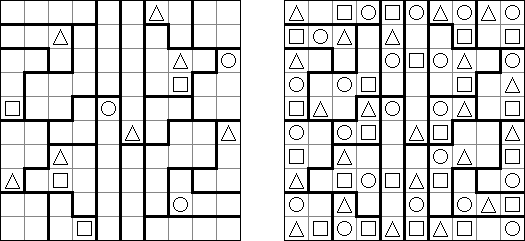
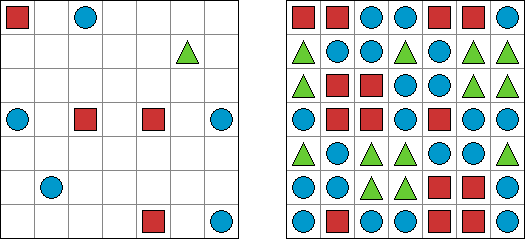
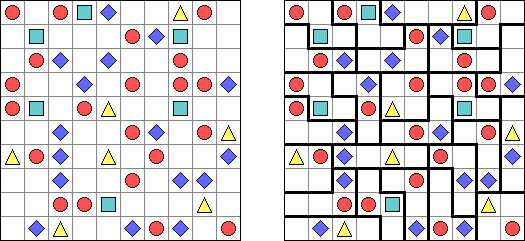
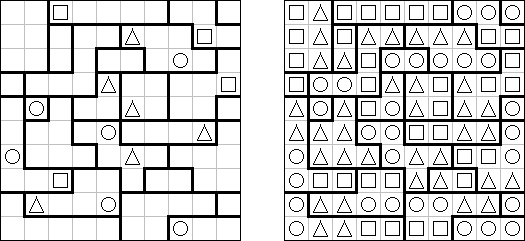
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.

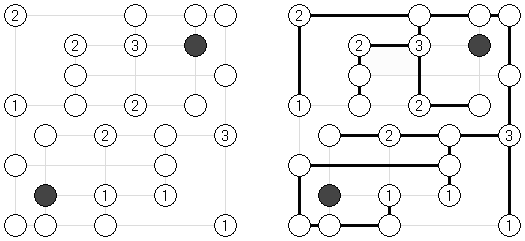
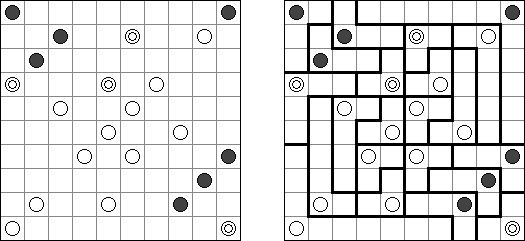
Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.

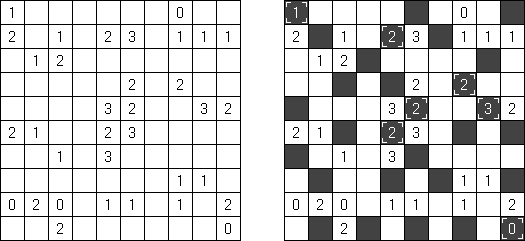
Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.

Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.

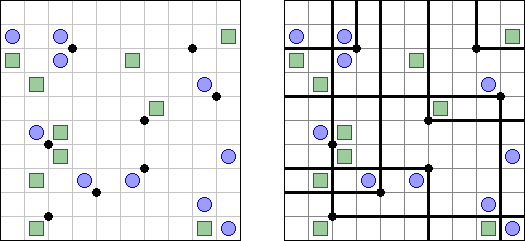
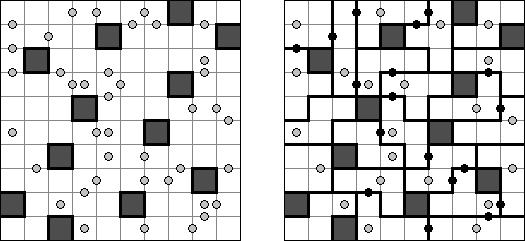
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.

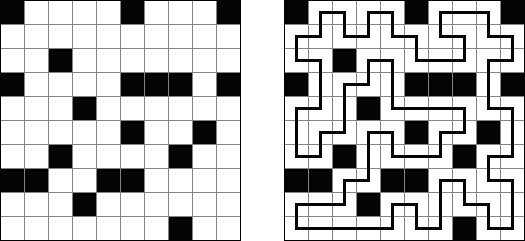
Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.

Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.

Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.

Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.

Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:

• White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle.
• Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.

Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.

Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.

Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.

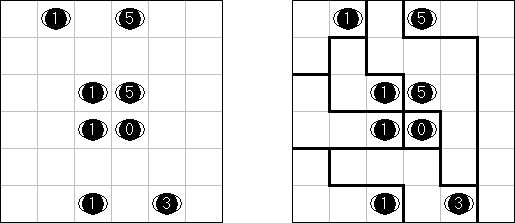
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.

Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.

Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.

Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.

Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:

• Each region contains exactly one arrow.
• Each two arrows are paired, they point to each other. There are no unpaired arrows.
• Two regions with paired arrows must not be horizontally or vertically adjacent.
• Between two paired arrows no other arrow must be placed.

Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.

Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.

Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.

Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• The black cells divide the grid in areas of white cells. Each area contains one cell with a number.
• Each area must have the same number of white cells as the number it contains (including the numbered cell).
• Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide.
• If two stripes are connected diagonally, the length of the stripes must be different.

Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.

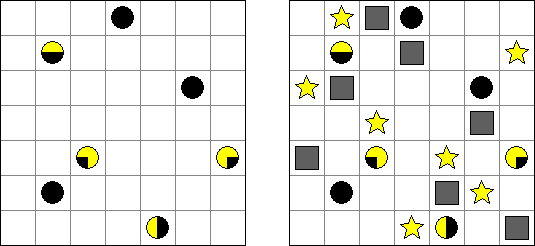
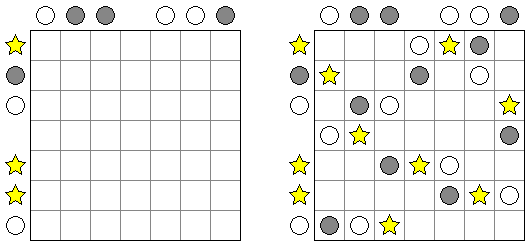
Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.

Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.

Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells).
• Two black cells must not be orthogonally adjacent.
• All of the white cells must be connected.

Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.

Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:

• Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake").
• Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed.
• Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached.
• The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.

Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.

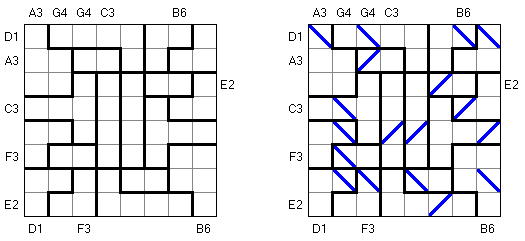
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.

Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.

Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• Two regions with the same amount of black cells must not be orthogonally adjacent.
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.

Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:

• Black cells must not be orthogonally connected.
• A cell with a number may be blacken.
• All the white cells must form an orthogonally continuous area.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.
• Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.

Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:

• A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally.
• A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all.
• A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells.
• Two snakes of the same length must not be orthogonally adjacent.
• A cell with a cross cannot be an end of a snake.

Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:

• Start at any stone.
• When a stone is encountered, it is picked up.
• When a stone is picked up, the direction can be changed.
• It is not allowed to reverse the direction.

Water Fun is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.

Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.

Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.

Santoitchi ("San to itchi"; from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• All white cells must be divided on regions having the size of exactly three cells.
• Two black cells must not be orthogonally adjacent.
• Each region contains a number.
• A number indicates how many black cells share an edge with that region.

Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.

Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.

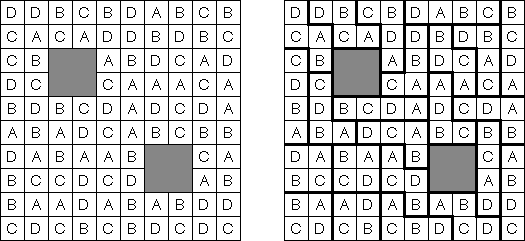
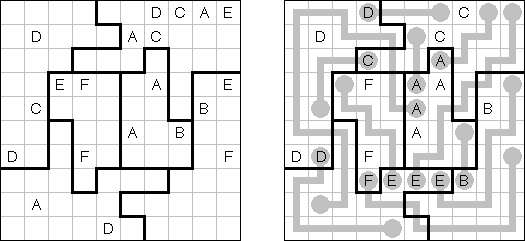
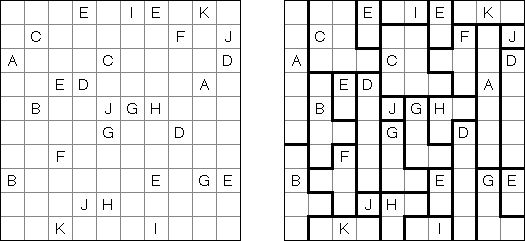
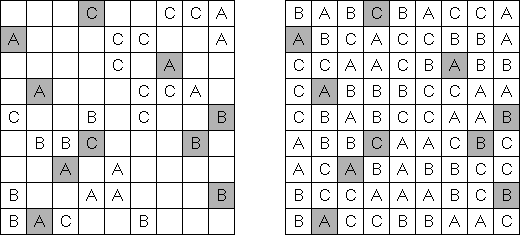
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.

Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.

EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.

Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.

Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.

Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.

Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:

• All black cells in a region must be connected horizontally or vertically.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• If all stones "fall down", they must cover exactly the bottom half of the grid.

Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.

Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.

Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.

Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:

• Cells with letters, circles or triangles are always white.
• White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide.
• A path from S to G includes all cells with circles and no cells with triangles.
• No 2 x 2 cell area within the grid can have the same color.
• All white cells must form an orthogonally continuous area.
• White cells must not form a loop.

Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:

• All black cells create a single connected group.
• No 2 x 2 cell area within the grid can contain all black cells.
• Numbered cells must not be black.
• Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.

Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.

Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:

• Each region contains one black circle.
• Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.

Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.

Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.

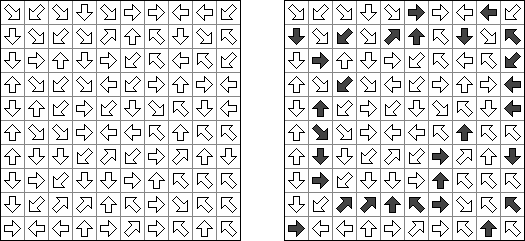
Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.

Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.

Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)

Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.

Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.

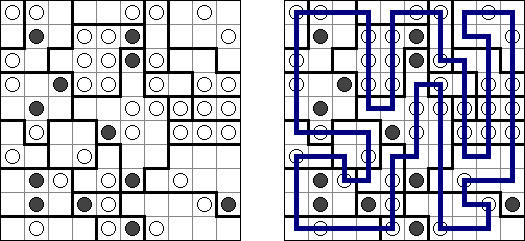
Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.

Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:

• Black cells form an area of square shape.
• No black areas touch each other horizontally or vertically (only diagonally).
• Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size.
• Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.

Golem Grad (an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:

• The black cells divide the grid into areas of white cells ("islands"), each containing at most one number.
• Two islands may not be connected.
• The island must have the same number of white cells as the number it contains.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the black color.
• All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid.
• Snakes must not cross each other.

Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:

• No two horizontally, vertically or diagonally adjacent cells contain a digit.
• The numbers across the top and down the left equal the row and column totals for the cells with numbers.
• The numbers across the bottom and down the right are the sums of numbers in the rows and columns.

Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.

Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• White cells form a path exactly one cell wide.
• Cells with circles are always white.
• A cell with a circle must have exactly one white cell adjacent to its side.
• A white cell without a circle must have at least two orthogonally adjacent white cells.
• A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself.
• All the white cells must be connected horizontally or vertically.
• No 2 x 2 cell area within the grid can have the same color.

Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:

• The white circle indicates that the sun is closer to the star than the moon.
• The black circle indicates that the moon is closer to the star than the sun.
• The star outside the grid indicates that the circles are at equal distance from the star in that row or column.

Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.

Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.

Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.

Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.

Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)

Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.

Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.

Nuraf ("Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells divide the grid into areas of white cells ("islands").
• Cells with numbers are always white.
• Two islands may not be connected.
• All of the black cells must be connected.
• No 2 x 2 cell area within the grid can have the black color.
• Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.

Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.

Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.

• The same arrows cannot be placed in adjacent cells.
• Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached.
• A cell with a number indicates a total number of arrows that leads to this cell.

Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.

Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.

Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.

Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)

Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.

Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.

Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.

Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.

Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.

Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.

Meandering Numbers (also known as "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)

Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.

Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.

From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.

Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.

Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.

Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.

Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)

Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.

Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).

Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.

Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).

Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.

Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.

Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.

Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.

Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.

Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.

SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.

Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border.
• A cell with a number indicates how many cells in the region must be blackened.
• No two black areas may share an edge.

Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.

Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.

Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

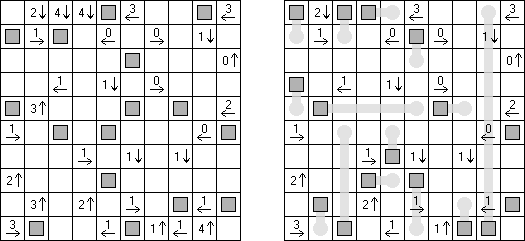
Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.

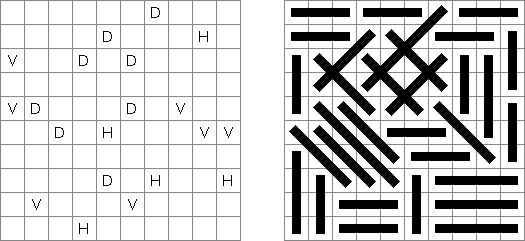
Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.

Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.

Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.

Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:

• The black cells form "islands". No two islands may share an edge; islands may be connected through their corners.
• If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island).
• All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners.
• If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).

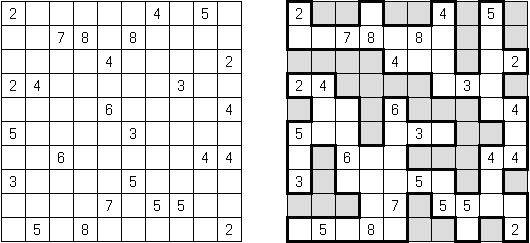
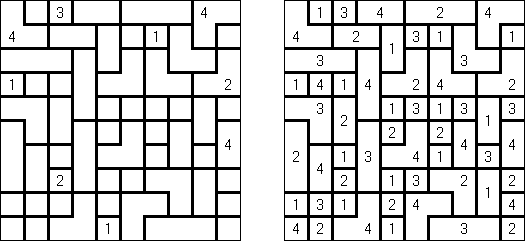
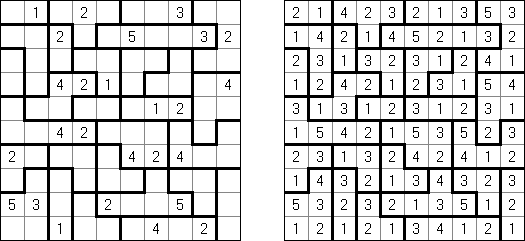
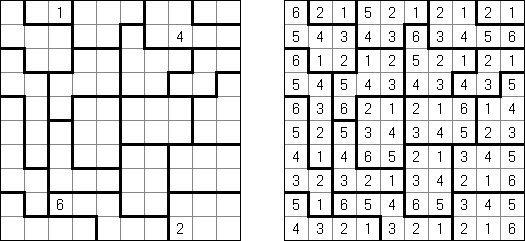
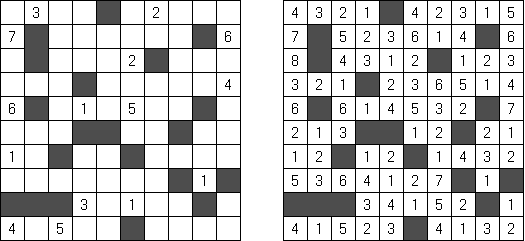
Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.

Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All white cells form one orthogonally connected area.
• A line of connected white cells cannot go through two or more region borders.

Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.

Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.

Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally).
• A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer.
• Each block contains exactly one number or a question mark.
• All blocks form "chains". A chain is a group of two or more blocks, connected through their corners.
• Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.

Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened.
• Blackened cells should not share an edge.
• All the white cells must be connected inside a region (it's possible for a region to have no white cells).
• If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions.
• All the white cells must form an orthogonally continuous area.

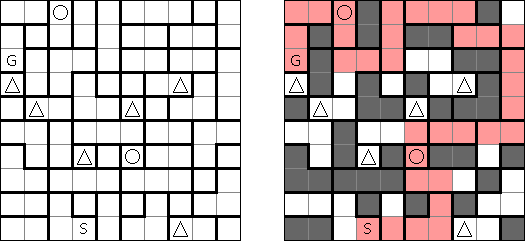
Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its N^th entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.

Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.

Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.

Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected horizontally or vertically (they form a "block").
• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any amount of cells may be blackened (all cells may stay white).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All blocks of black cells must be connected to each other through their corners.
• No 2 x 2 cell area within the grid can contain all black cells.

Kazoku ("Kazoku shashin"; from Japanese, literally "family photo") is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.

Tontonbeya (from Japanese, literally "gambler") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.

Context is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:

• All the white cells must be connected horizontally or vertically.
• A cell with a number can be blacken. Two black cells must not be orthogonally adjacent.
• The number in a white cell indicates the number of orthogonally adjacent black cells.
• The number in a black cell indicates the number of diagonally adjacent black cells.

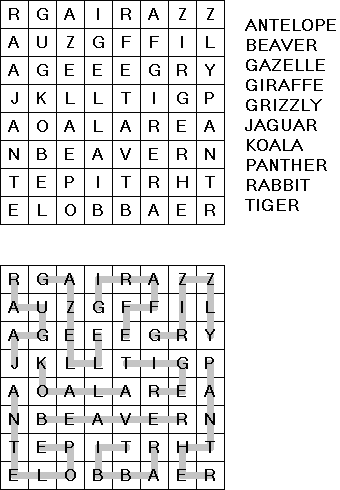
Word Finder (단어 찾기)는 글자가 있는 격자로 되어 있다. 이 퍼즐의 목표는 격자 내에 숨어 있는 단어를 찾아서 표시하는 것이다. 각 단어에 들어 있는 글자는 직각으로 접해 있다. 각 단어는 하나의 단어에서만 사용될 수 있다.

단어 목록은 퍼즐을 만들 때 제공되어야 한다. 키워드도 정의할 수 있는데, 이 단어는 격자에서 남아있는 글자들로 만들어진다.

Nine Letters (아홉 문자)는 Word Finder (단어 찾기) 퍼즐의 변형이다. 이 게임은 문자가 있는 격자로 되어 있다. 격자는 3×3 하위 격자로 나뉜다. 이 게임의 목표는 각 하위 격자 내부에 숨겨진 단어를 찾아서 표시하는 것이다.

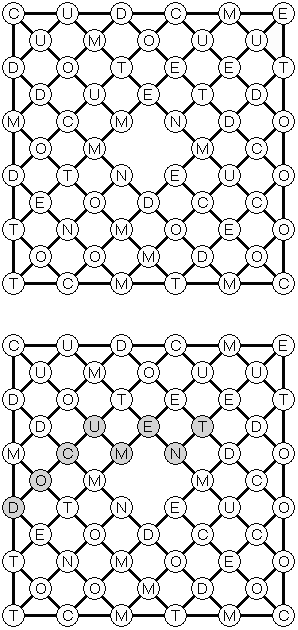
Spider Web (거미줄)은 선으로 연결된 동그라미들로 되어 있다. 각 동그라미에는 하나의 글자가 있다. 목표는 동그라미 그물 안에 숨어 있는 키워드를 찾아서 표시하는 것이다.

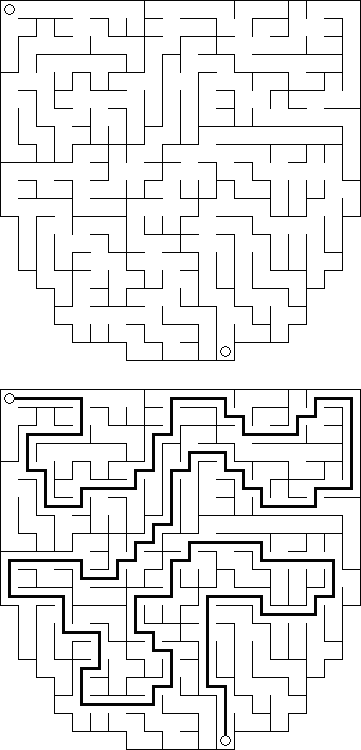
Maze (미로)는 복잡한 경로 또는 통로망으로 구성된 퍼즐이다. 목표는 선택된 두 지점 사이의 경로를 찾는 것이다. Cross+A 는 직사각형, 정사각형 또는 불규칙한 모양의 퍼즐을 만들 수 있다.