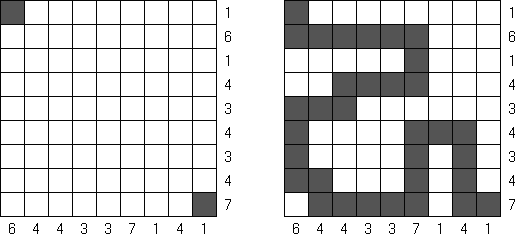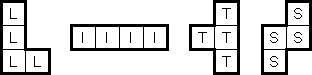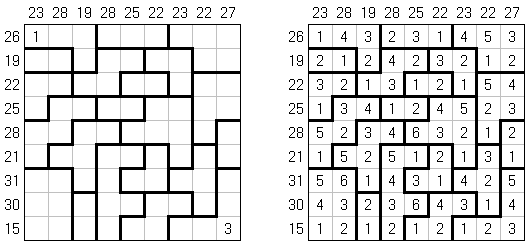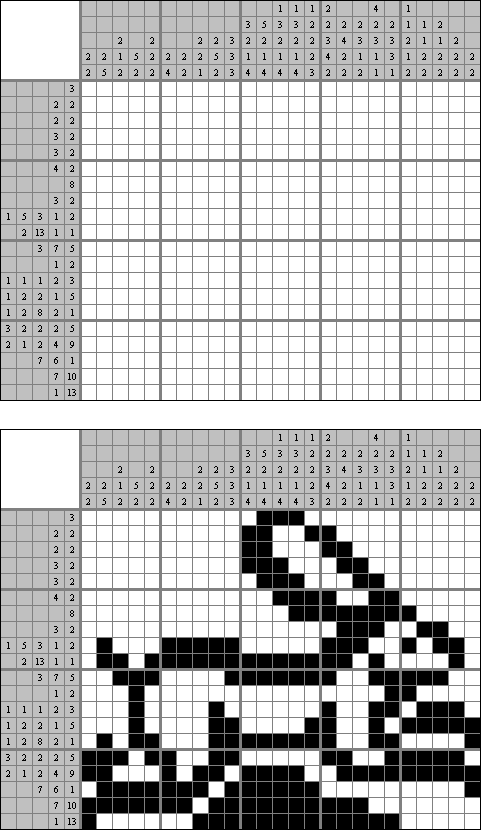
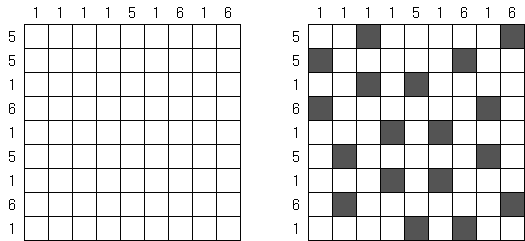
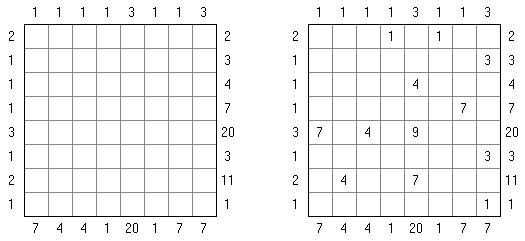
Cross+A Quebra-cabeças

Cross+A resolve e cria uma grande quantidade de diferentes quebra-cabeças lógicos. O quebra-cabeça criado pode ser salvo como um arquivo de imagem (os formatos suportados incluem BMP, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF, metarquivos Windows e arquivos CorelDRAW). Também está disponível o modo batch para criar quebra-cabeças.

Nonograma ("Hanjie", "Paint by Numbers", "Griddler") é um quadrado ou retângulo, o objetivo é desenhar as figuras de acordo com os números prescritos de um jeito especial; os números no lado esquerdo da fileira e na parte de cima das colunas mostram a quantidade dos grupos das células pretas na linha correspondente e a quantidade das células pretas unidas de cada grupo. Os grupos são separados por no mínimo uma célula vazia.

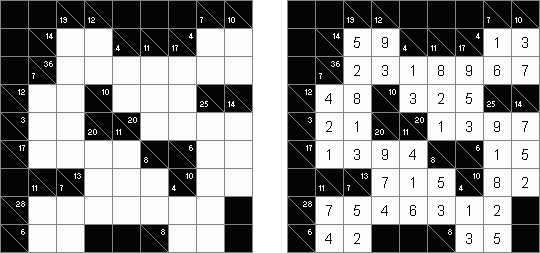
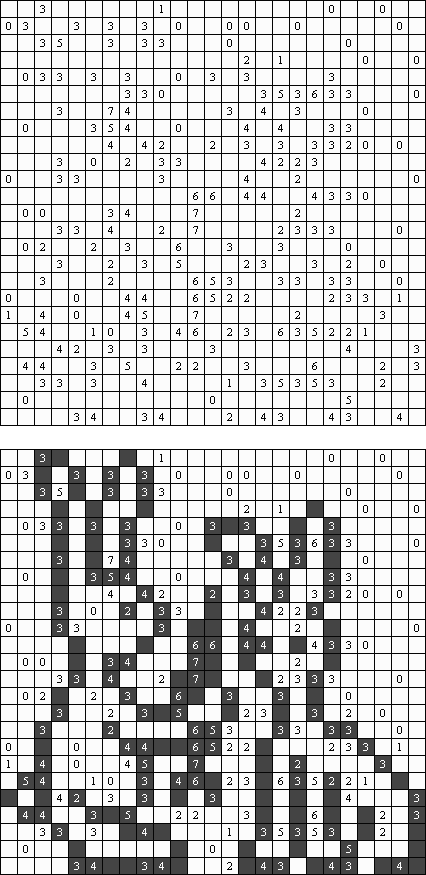
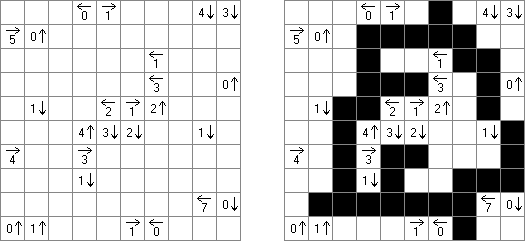
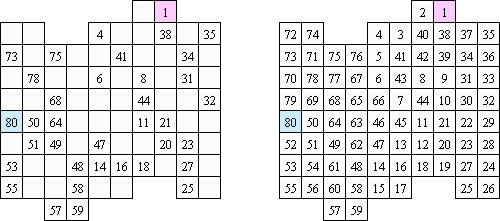
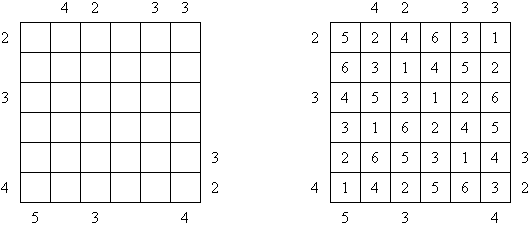
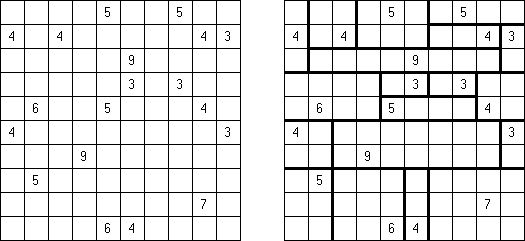
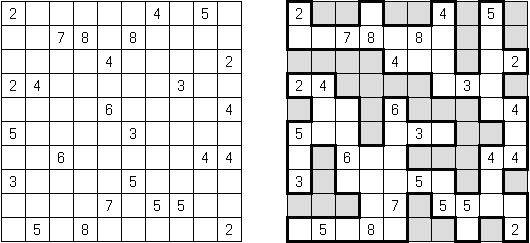
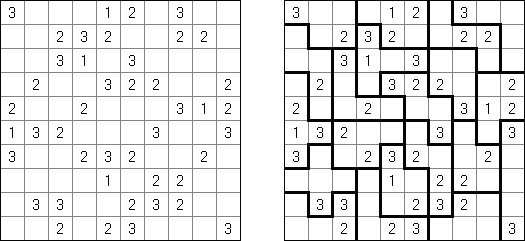
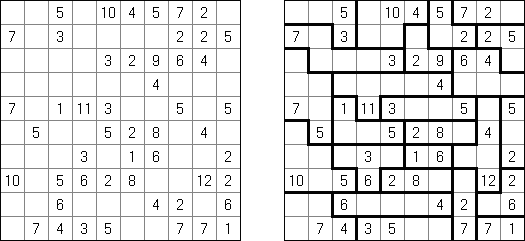
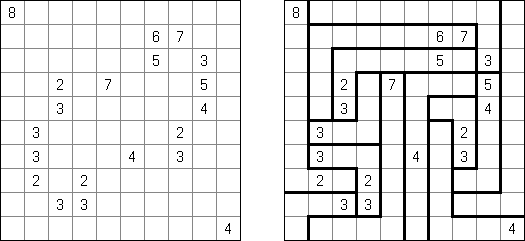
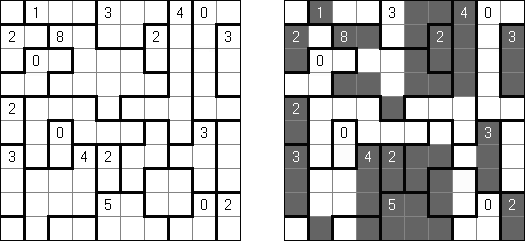
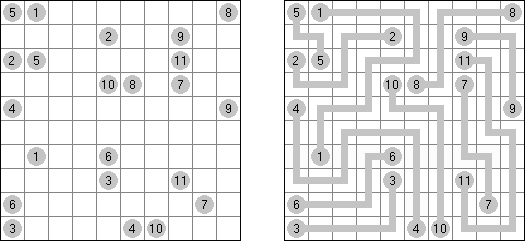
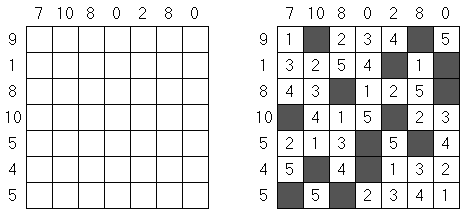
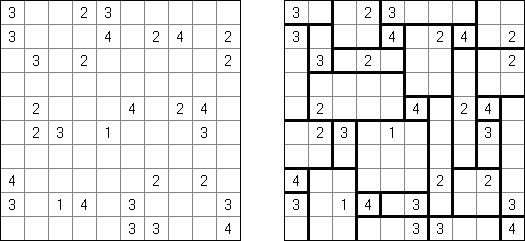
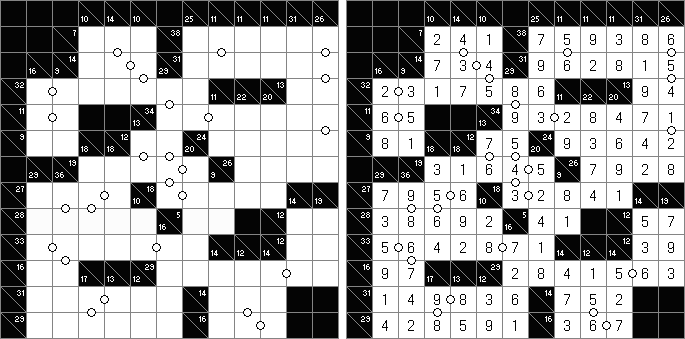
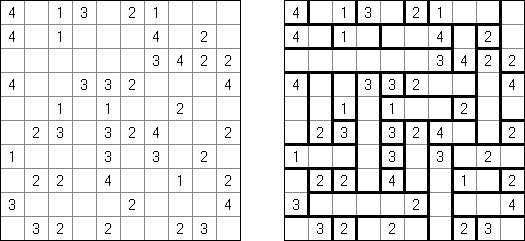
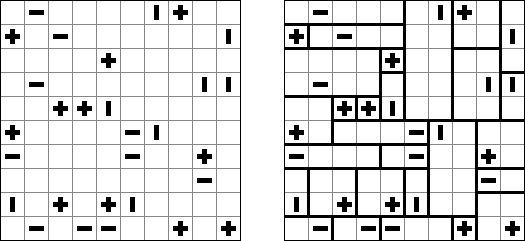
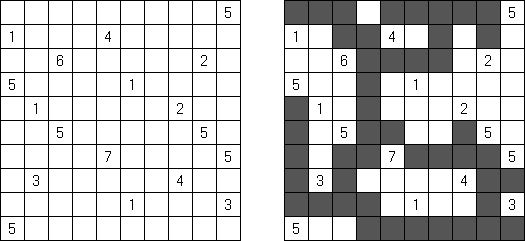
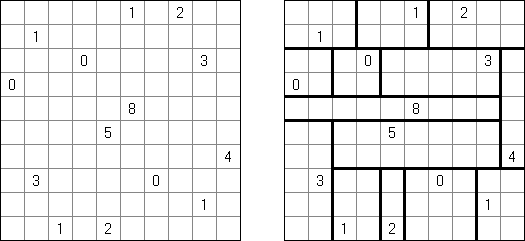
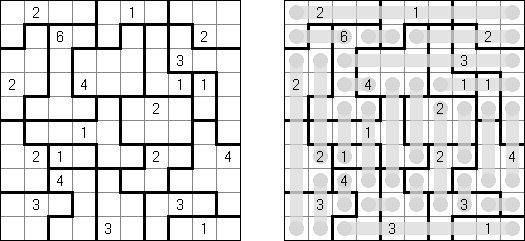
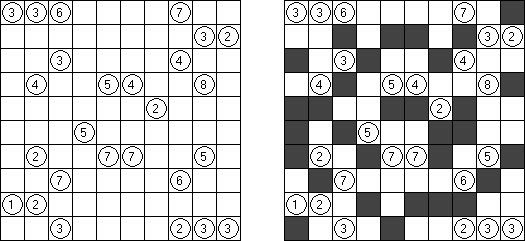
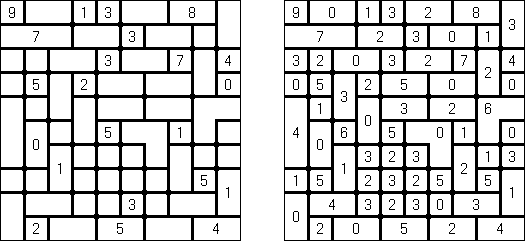
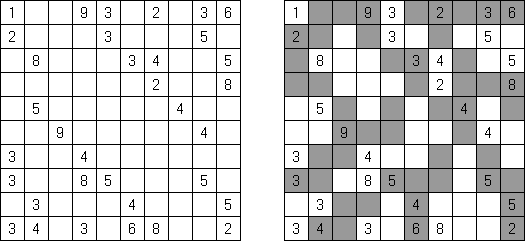
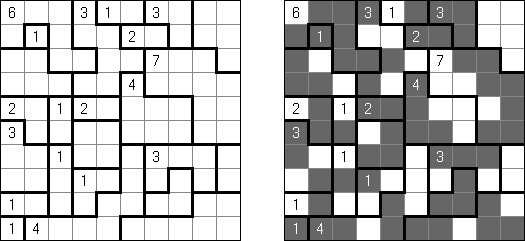
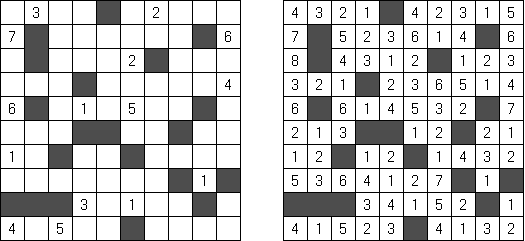
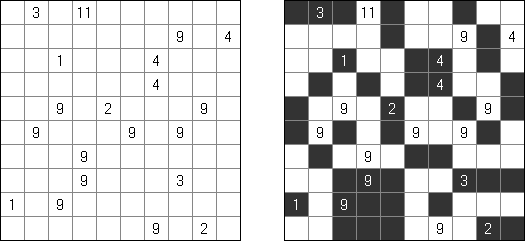
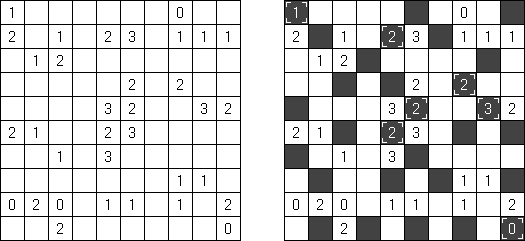
Kakuro ("Cross Sums") é um quebra-cabeça numérico, análogo matemático de palavras cruzadas. O objetivo dele é preencher as células com números de 1 a 9 sendo que algumas células são inativas (marcadas com a cor preta). Nas células com os valores numéricos prescritos, o valor encima da parte da direita significa o valor sumário dos números na fileira, e o valor embaixo da parte da esquerda é igual ao valor sumário dos números da coluna que fica abaixo da célula. Por exemplo, o número 6 pode ser apresentado como o valor sumário de 1 e 5, 2 e 4; os números iguais (3 e 3) não podem ser utilizados.

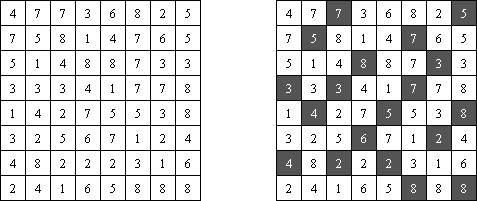
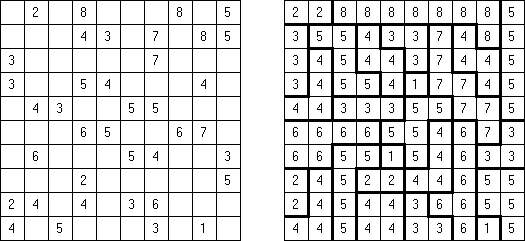
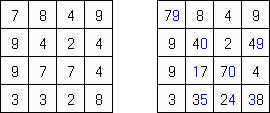
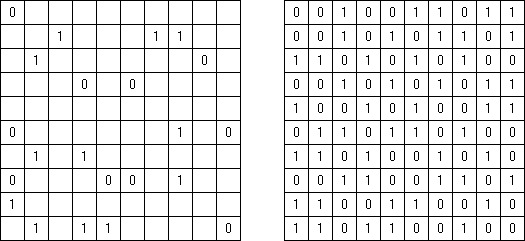
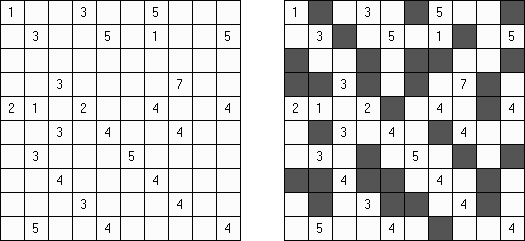
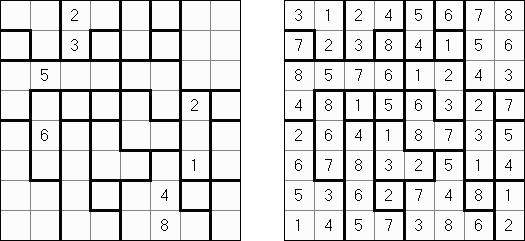
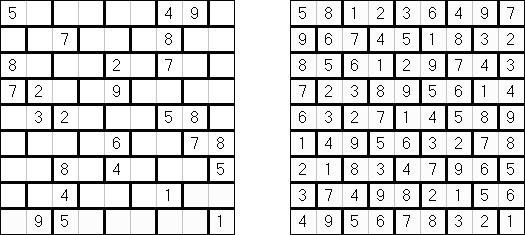
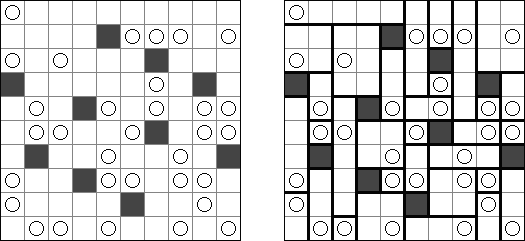
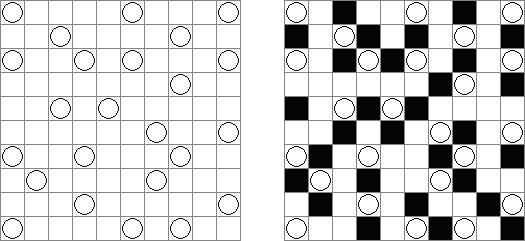
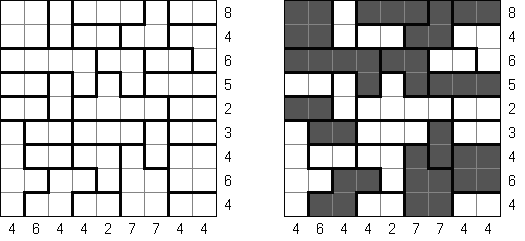
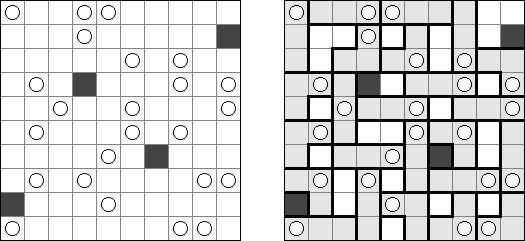
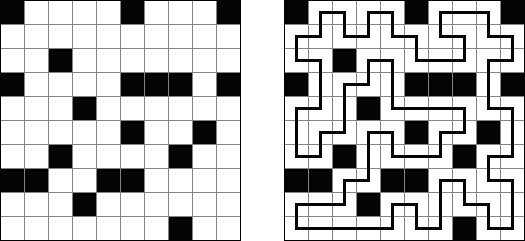
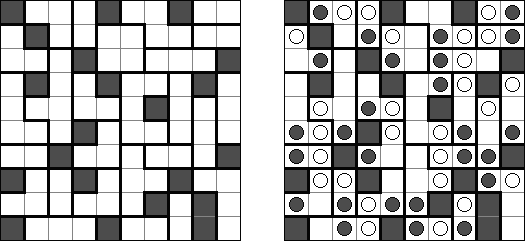
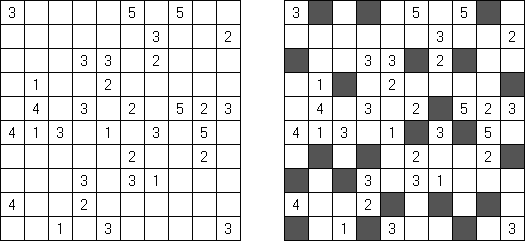
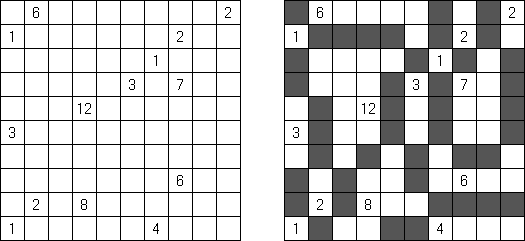
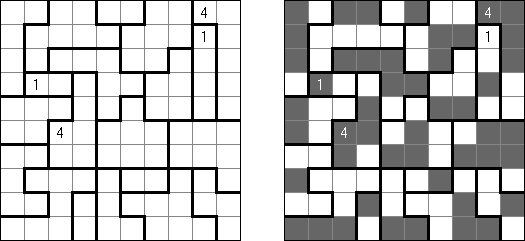
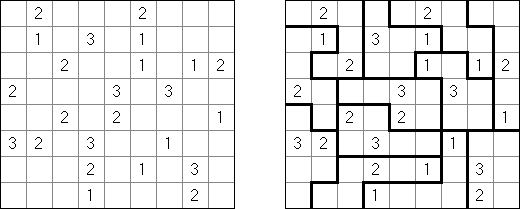
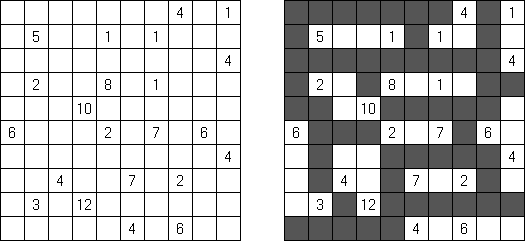
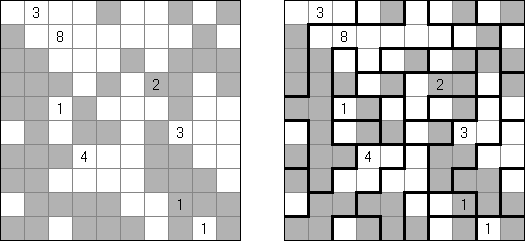
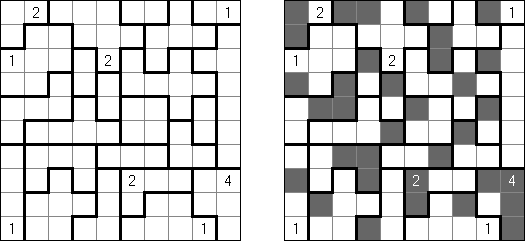
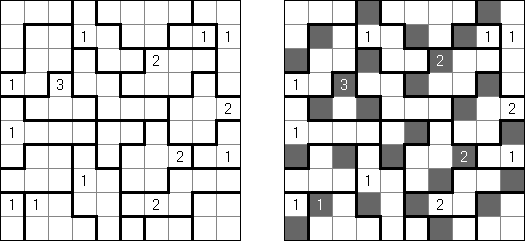
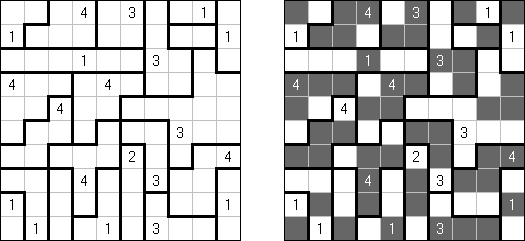
Hitori é um quebra-cabeça lógico. O objetivo dele é riscar os números repetidos de tal maneira que nenhum deles se encontre mais de uma vez em qualquer linha ou coluna. As células riscadas podem entrar em contato entre si somente com os seus ângulos, mas não com os seus lados. As células não riscadas devem compor um espaço continuo branco, quer dizer que nenhuma delas deve ser isolada das células do mesmo tipo.

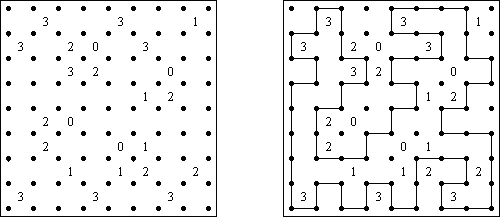
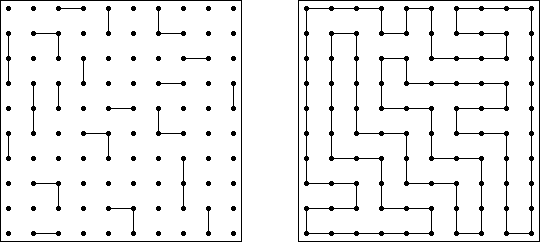
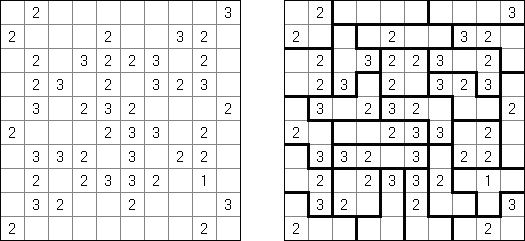
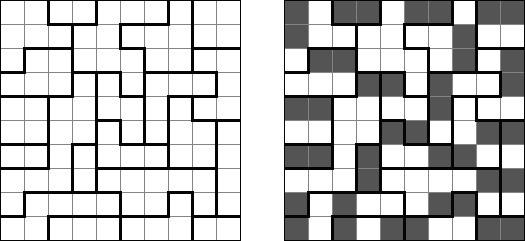
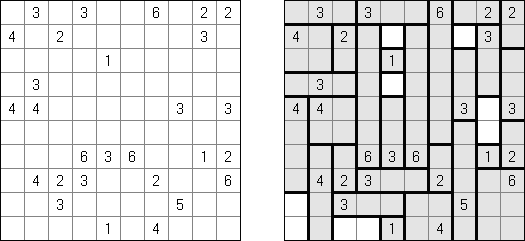
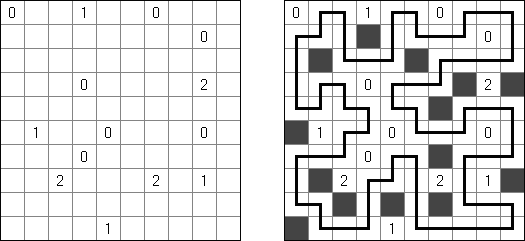
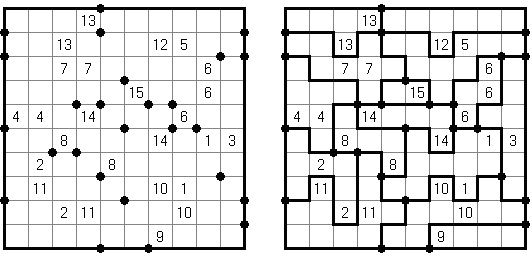
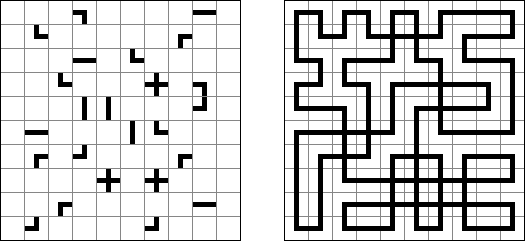
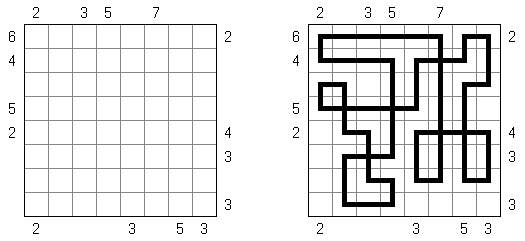
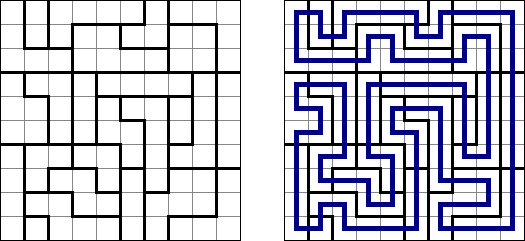
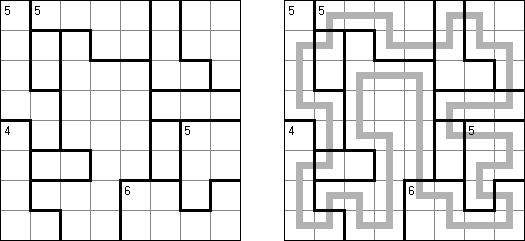
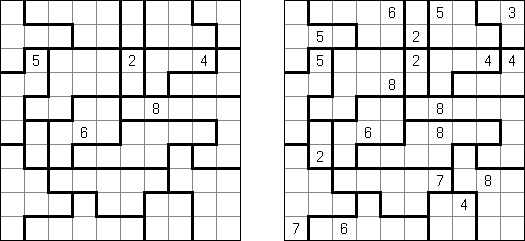
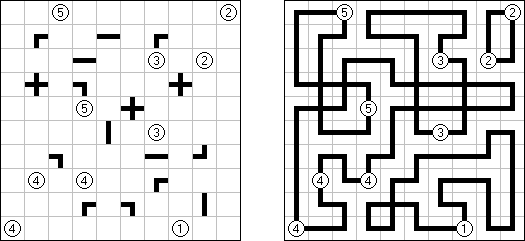
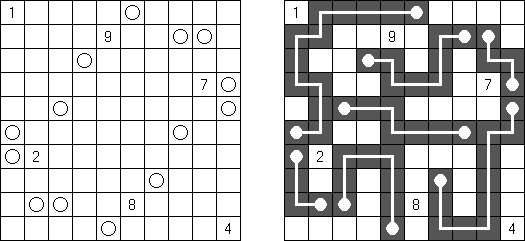
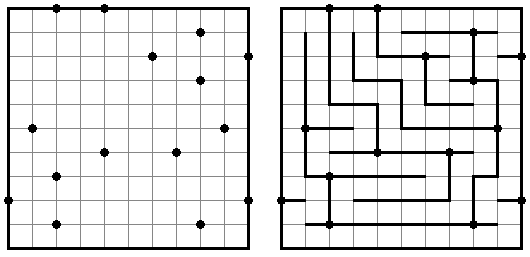
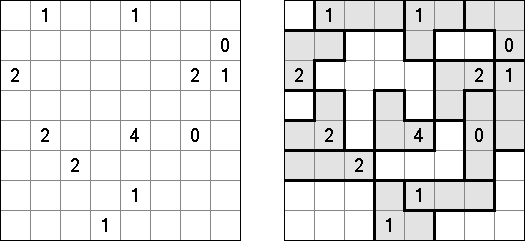
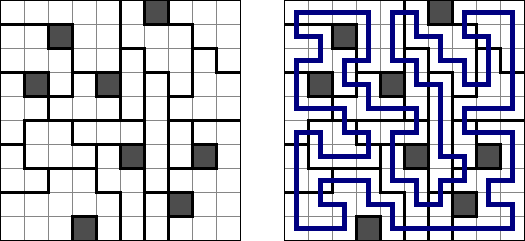
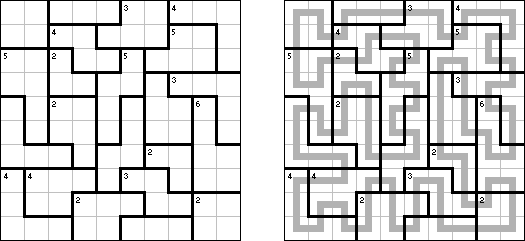
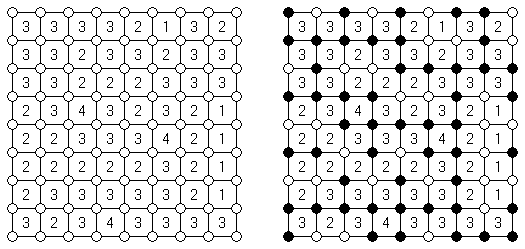
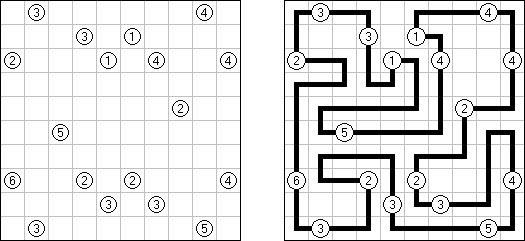
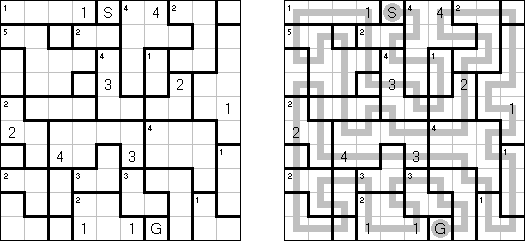
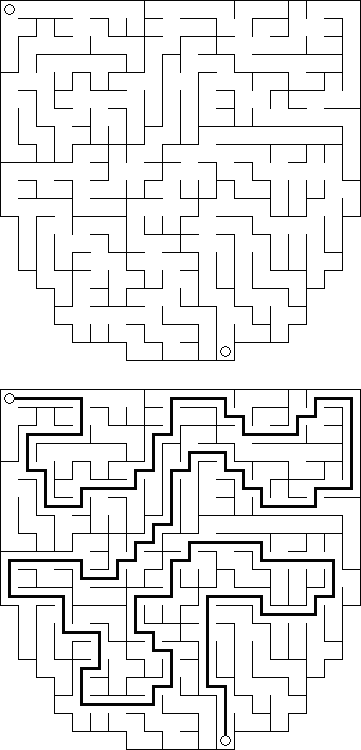
Slitherlink ("Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin") é um quebra-cabeça lógico que parece com um labirinto. O objetivo deste quebra-cabeça é ligar os pontos com os segmentos verticais e horizontais de tal maneira que saia um ponto fechado que não atravesse a si mesmo. Cada número indica a quantidade dos segmentos que devem ser dispostos em volta do perímetro dele. Se não há nenhum número na célula, isso significa que qualquer quantidade de linhas pode ser colocada.

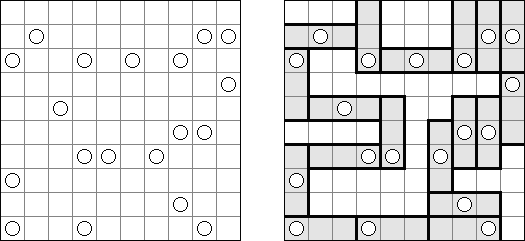
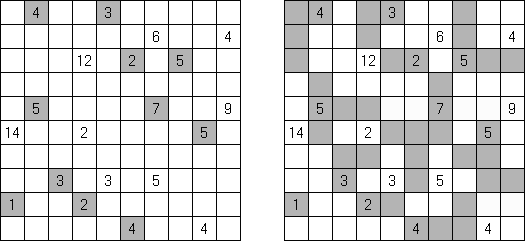
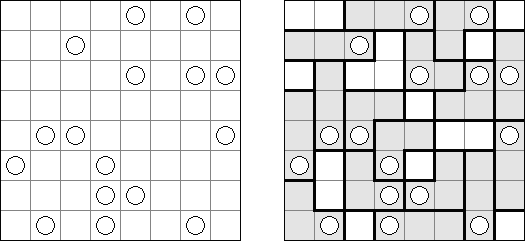
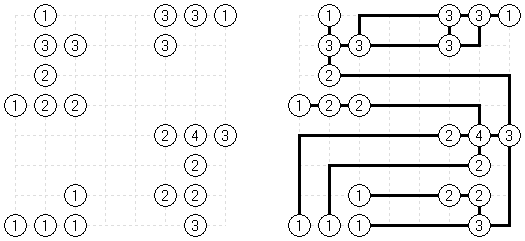
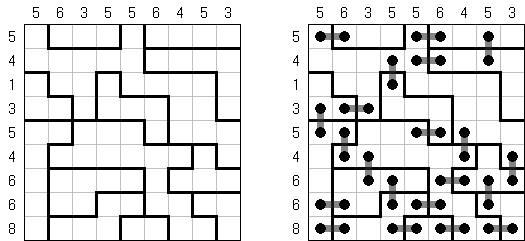
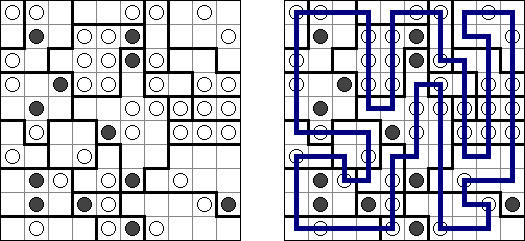
Link-a-Pix ("Paint by Pairs") é um outro quebra-cabeça numérico. Todos os números (com a exceção de 1) dispostos na rede têm o seu par equivalente. O objetivo é achar cada par dos números e ligá-los por meio de linhas. A quantidade de células da rede deve ser igual aos números nos seus lados. As linhas que ligam os pares podem refratar-se e ir tanto na direção vertical, quanto na horizontal, mas não na diagonal. As linhas podem atravessar-se ou ir através das mesmas células.

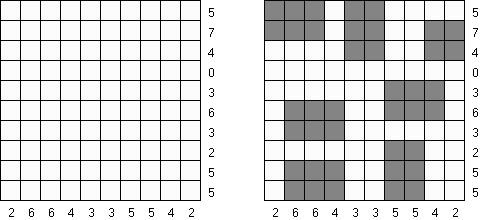
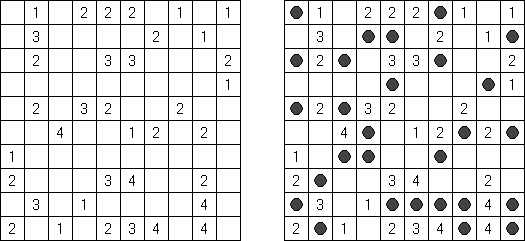
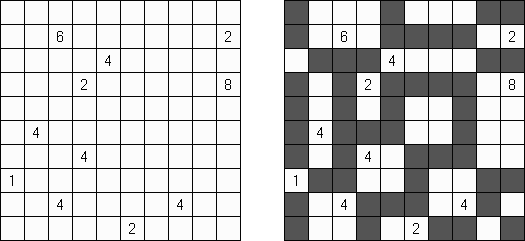
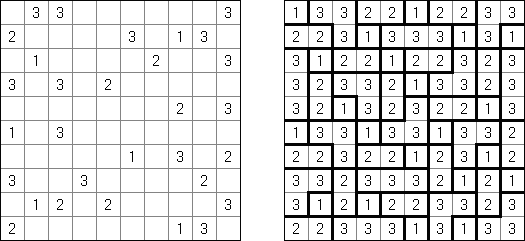
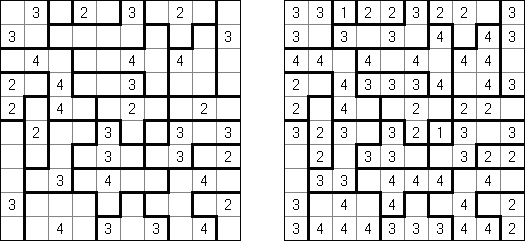
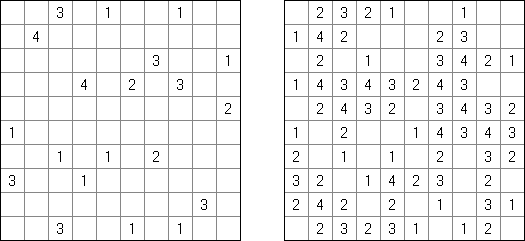
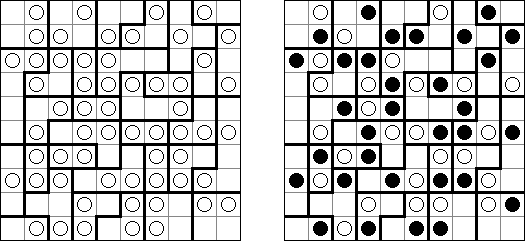
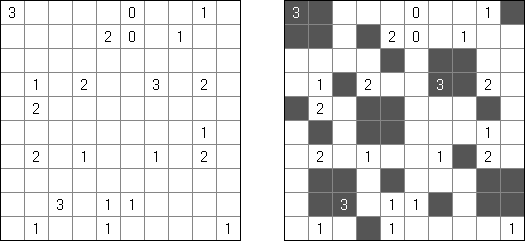
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") é um quebra-cabeça lógico com uma imagem codificada por meio de números. Cada número indica a quantidade de células adjacentes (contando também aquela que contém número) a serem coloridas. Por exemplo, se a célula contém zero, então nem ela, nem as células vizinhas serão coloridas.

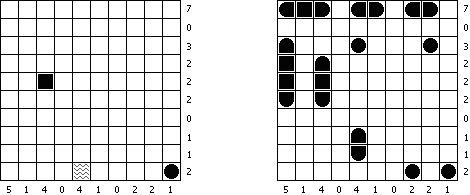
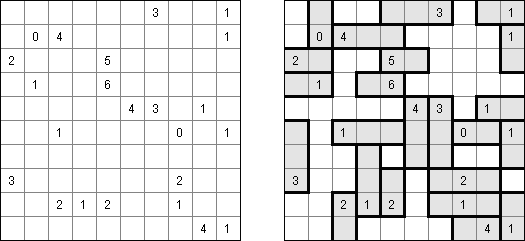
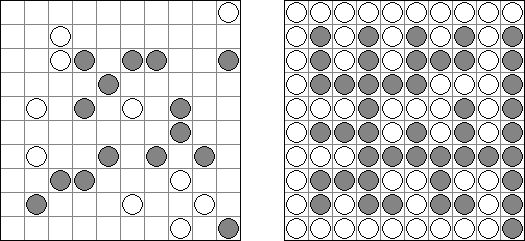
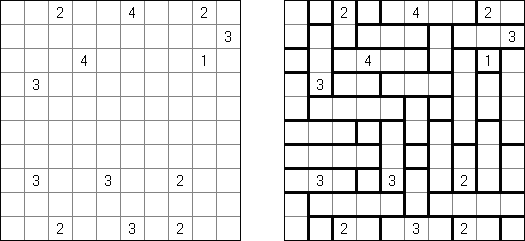
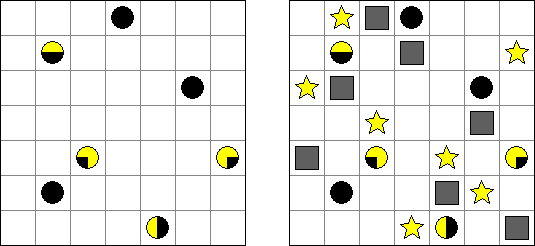
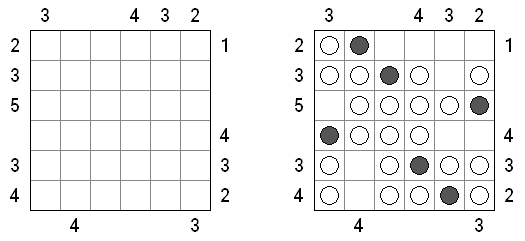
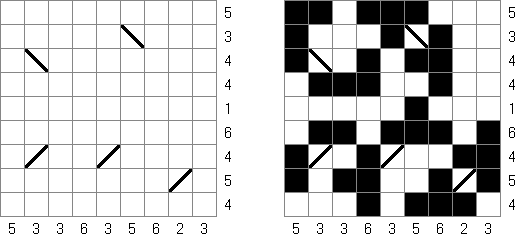
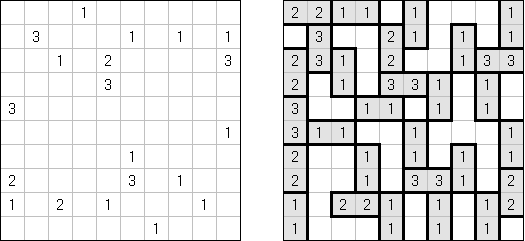
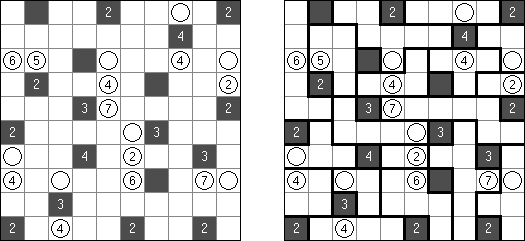
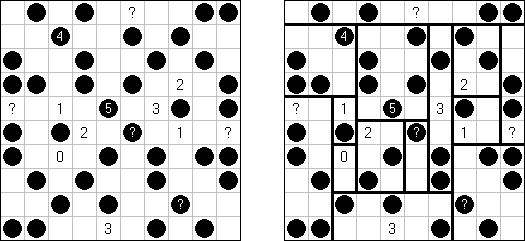
Batalha naval ("Battleships", "Solitaire Battleships", "Battleship Solitaire") é um quebra-cabeça com as regras parecidas com o jogo popular. O objetivo é dispor os "navios" de tal maneira que eles não entrem em contato entre si, mesmo com os seus ângulos. Os números escritos do lado e embaixo significam a quantidade dos fragmentos de navios que entram em uma linha ou coluna.

As medidas padrão do campo é 10 x 10. Há um navio que ocupa 4 células, dois navios que ocupam 3 células, três navios que ocupam 2 células e quatro navios que ocupam 1 célula. As vezes alguns fragmentos dos navios são abertos.

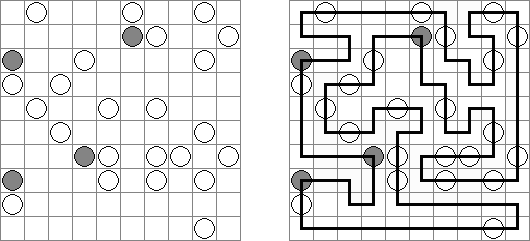
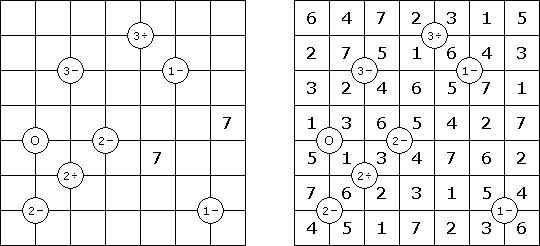
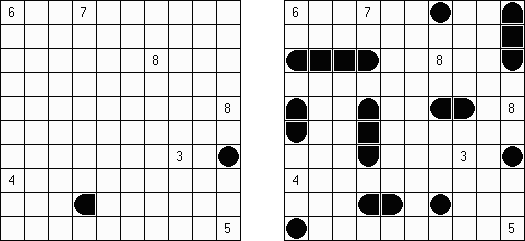
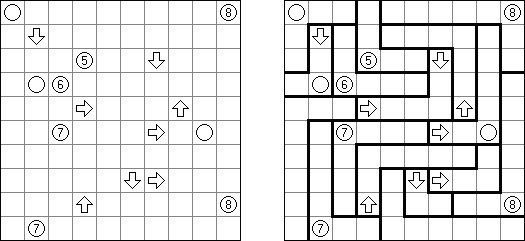
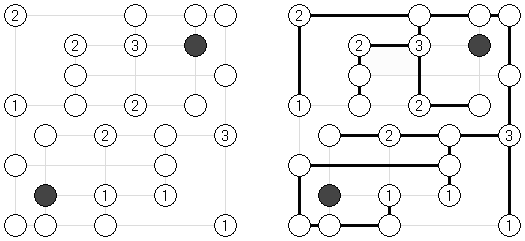
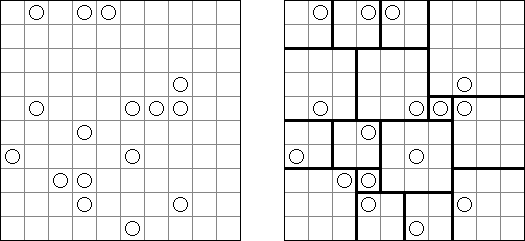
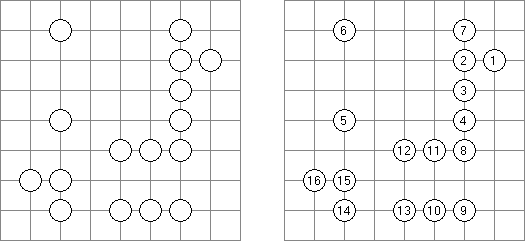
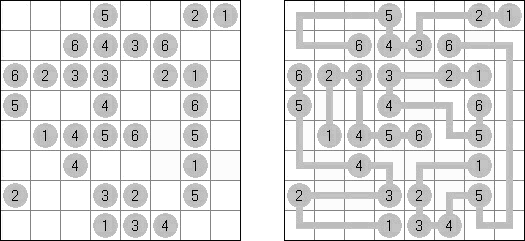
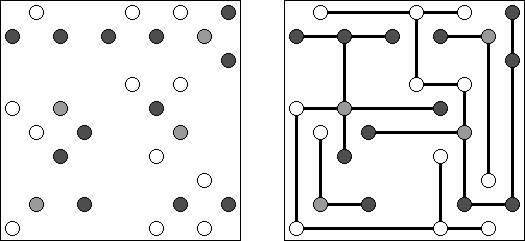
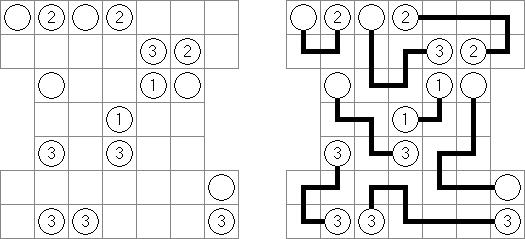
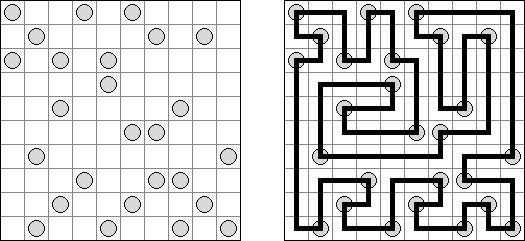
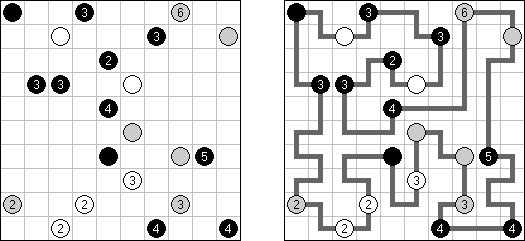
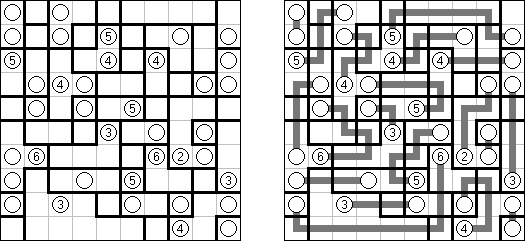
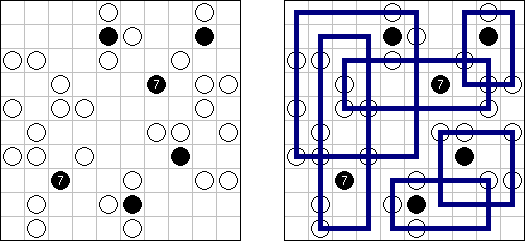
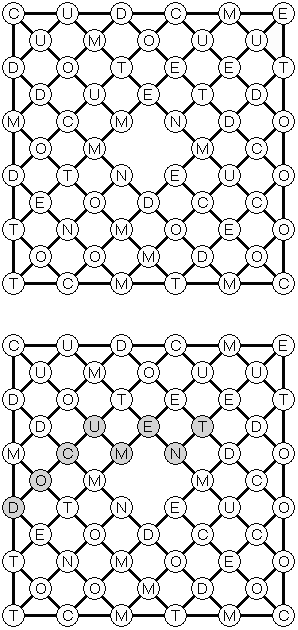
Hashiwokakero ("Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai") é um quebra-cabeça cujo o objetivo é ligar os círculos contendo números ("ilhas") com as linhas retas ("pontes"). Um número escrito na ilha mostra a quantidade das pontes que devem ser construídas na sua direção. Nenhuma das ilhas deve ser isolada; as linhas devem ser traçadas de tal maneira que cada ilha seja conectada com qualquer outra ilha por meio de pontes.

É permitido construir somente até duas pontes entre cada duas ilhas. As linhas podem ir tanto na direção vertical, quanto na horizontal, mas não na diagonal. Eles não podem refratar-se, atravessar-se e ir através das ilhas.

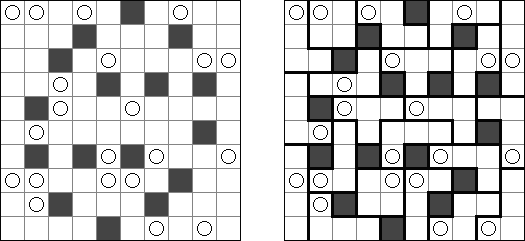
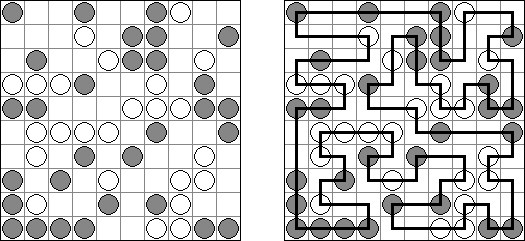
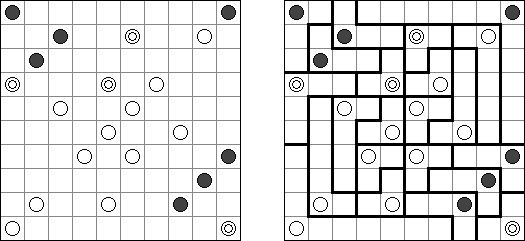
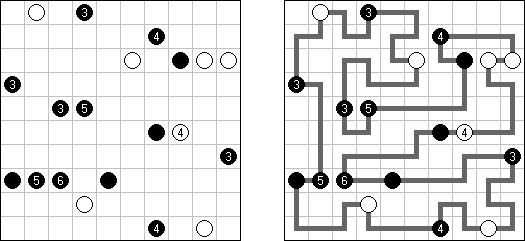
Masyu ("Shiroshinju Kuroshinju", "White Pearls and Black Pearls") é um quebra-cabeça lógico, cujo o objetivo é ligar os círculos brancos e pretos por meio dos segmentos retos de tal maneira que a linha única fechada seja criada. A linha deve ir reta através dos círculos brancos, mas deve virar na célula seguinte ou antecedente (ou nas duas). Quando a linha atravessa um círculo preto, ela deve virar 90 graus, porém na célula seguinte ou antecedente não é permitido virar.

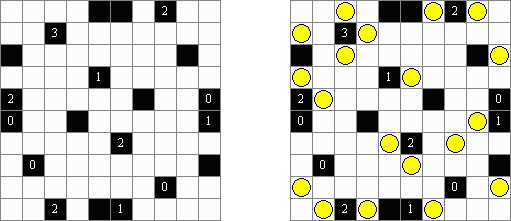
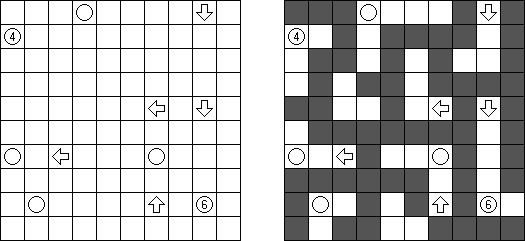
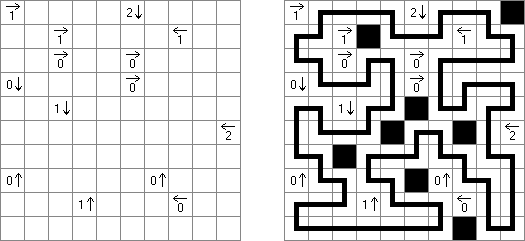
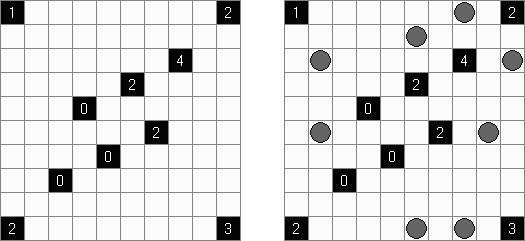
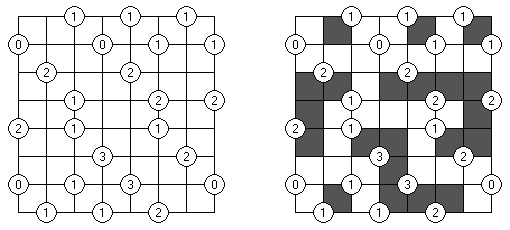
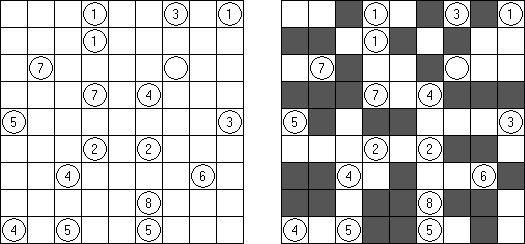
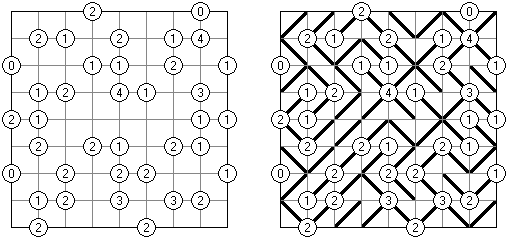
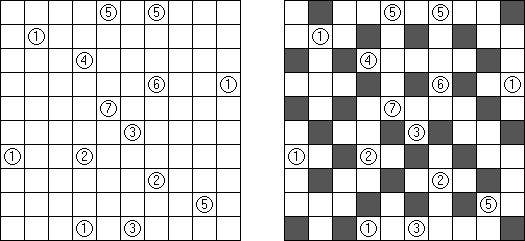
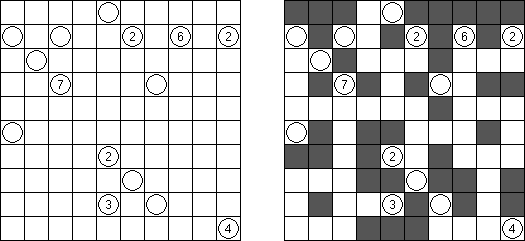
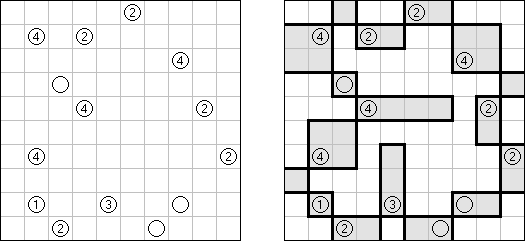
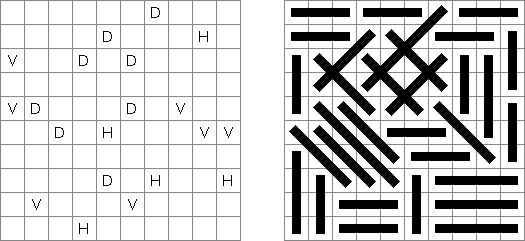
Akari ("Light Up", "Bijutsukan") é um quebra-cabeça lógico. O campo do quebra-cabeça é composto por células brancas e pretas, algumas células pretas contém números. O objetivo é dispor as "luzes" nas células brancas de tal maneira que o campo todo seja iluminado, mas as lanternas não "iluminem" uma a outra.

A luz da lanterna pode ir para a direção horizontal, quanto para a direção vertical, mas pode ser bloqueada por uma célula preta. Uma célula preta pode conter um número de 0 a 4 indicando a quantidade de lanternas que deve ser dispostas em volta dela (as lanternas colocadas na diagonal dessa célula preta não são consideradas). Caso a célula não contenha números, qualquer quantidade de lanternas pode ser colocada em volta dela.

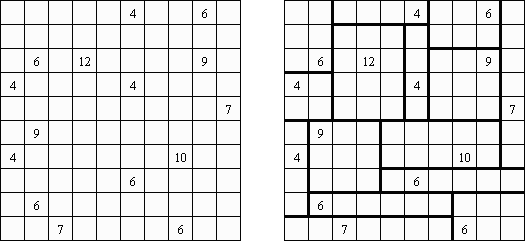
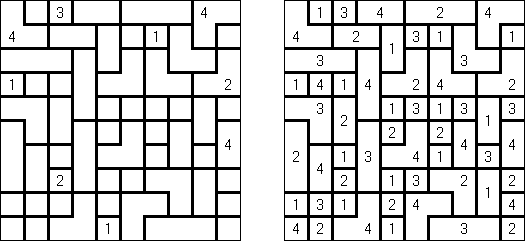
Fillomino ("Polyominous") é uma rede retangular de tamanho livre; algumas células contêm números. O objetivo é dividir o campo do jogo em blocos; cada bloco deve conter a quantidade de células de acordo com o número que o bloco contém. Os blocos que têm o mesmo tamanho não devem estar em contato entre si nas direções horizontal e vertical. As células que inicialmente não têm números podem ser reunidas em blocos necessários para a solução do quebra-cabeça.

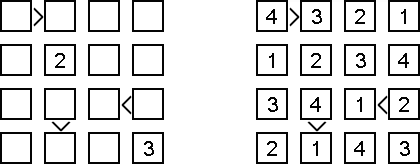
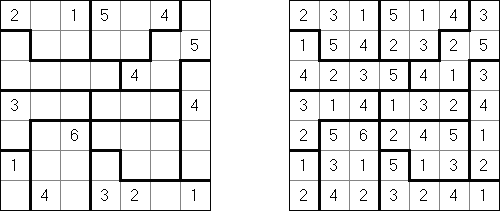
Futoshiki ("Hutoshiki", "Unequal") é um outro quebra-cabeça de números. O campo do jogo é uma rede quadrada; algumas células podem conter números; os sinais "<" e ">" podem estar presentes indicando as correlações estabelecidas entre os números vizinhos. O objetivo do jogo é preencher as células livres com números de tal jeito que cada número se encontre em cada linha e cada coluna somente uma vez.

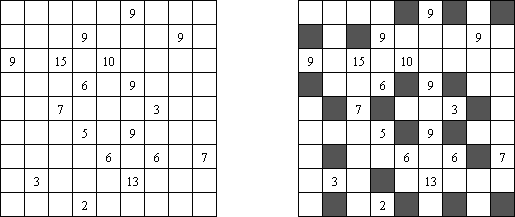
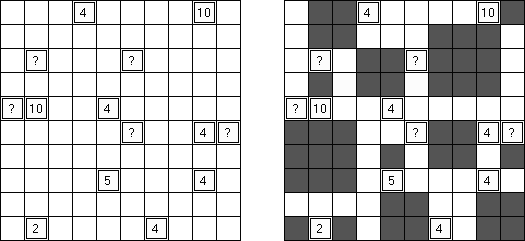
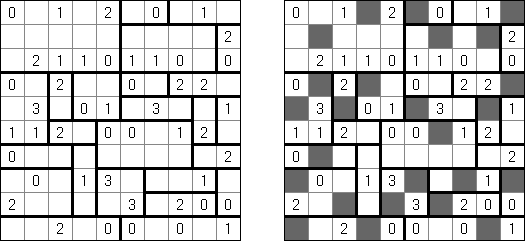
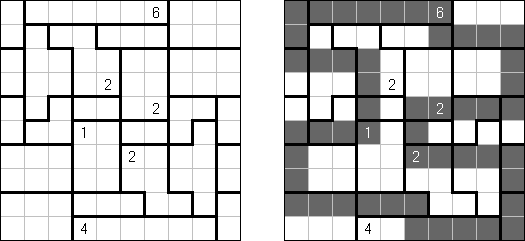
Kuromasu ("Kurodoko", "Where is Black Cells?") é uma rede retangular cujas algumas células contém números. O objetivo é colorir as células com a cor preta observando as seguintes condições:

• Cada número significa a quantidade das células brancas "visíveis" dessa célula nas direções vertical e horizontal; "o olhar" estende-se até o momento em que ele atinja a extremidade do campo ou uma célula da cor preta.
• As células com os números sempre ficam brancos.
• As células pretas não podem entrar em contato entre si nas direções vertical ou horizontal.
• Todas as células brancas compõem o campo único branco, então eles entram em contato entre si nas direções vertical e horizontal.

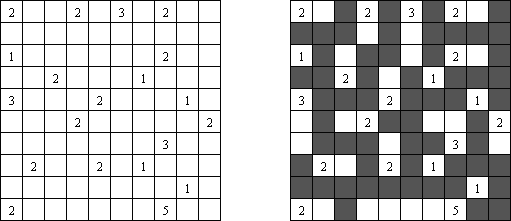
Nurikabe ("Cell Structure", "Islands in the Stream") é um quebra-cabeça lógico de números. Na mitologia japonesa o "nirikabe" é um monstro com a aparência de uma parede invisível que defende a passagem.

O objetivo é restaurar a mapa com a disposição das ilhas observando as seguintes regras:

• A informação sobre cada ilha é apresentada como um número que indica a quantidade das células que ocupa esta ilha.
• Qualquer duas ilhas podem entrar em contato entre si somente com os seus ângulos.
• Todas as ilhas contêm somente um número nas suas descrições.
• Um rio está no meio das duas ilhas.
• Todas as células do rio devem ser ligadas entre si.
• O mapa não pode conter nenhum quadrado do tamanho 2 x 2, cujas todas as células contêm rio.

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

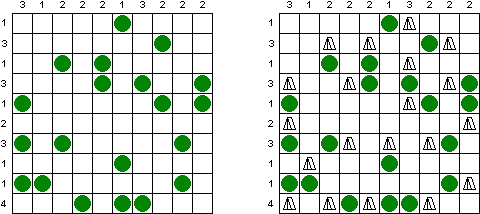
Tents ("Tents and Trees") é uma rede retangular, cujas algumas células contêm "árvores". O objetivo é dispor as "barracas" perto das árvores observando as seguintes regras:

• A quantidade das barracas deve ser igual à quantidade de árvores.
• Cada barraca deve ser disposta perto da "sua" árvore tanto na direção vertical, quanto na horizontal, mas não na diagonal. Caso essa condição seja comprida, a disposição da barraca em relação às "outras" árvores não é importante.
• Duas barracas não podem estar nas células vizinhas, inclusive na diagonal.
• Os números escritos do lado e encima significam a quantidade de barracas que estão em uma linha ou coluna.

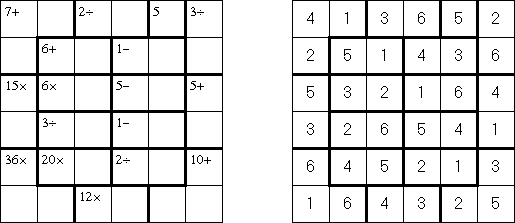
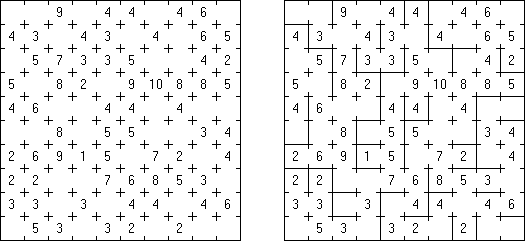
Calcudoku ("KenKen", "KENKEN", "KenDoku", "Square Wisdom") é um quebra-cabeça matemático e lógico. O objetivo do jogo é preencher a rede com números de tal jeito que não exista as repetições de números em cada linha e cada coluna. O número em ângulo de cada bloco escolhido é o resultado da operação aritmética sobre os números deste bloco. A diferença entre este quebra-cabeça e suduku assassino (Killer Sudoku) é que os números dentro de um bloco podem ser repetidos.

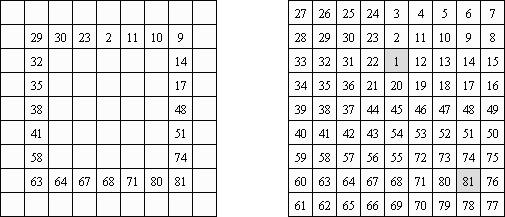
Hidato (tradução de ídiche significa o "meu quebra-cabeça"; "Hidoku") foi inventado por um matemático israelense Gyora Benedek. O quebra-cabeça é o campo de tamanho livre (normalmente retangular ou quadrado) composto de células. O objetivo do jogo é preencher todas as células com os números consecutivos ligados horizontalmente, verticalmente e na diagonal. Os números menores e maiores já estão indicados, assim como os outros números facilitando o processo da solução do quebra-cabeça e fornecendo a unicidade da solução do problema.

Numbrix é um tipo de quebra-cabeça lógico; é uma rede retangular cujas algumas células contêm números. O objetivo é preencher as células vagas de tal maneira que todos os números sejam ligados consecutivamente, na horizontal ou na vertical. O deslocamento na horizontal não é permitido.

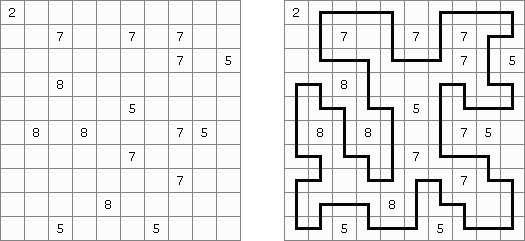
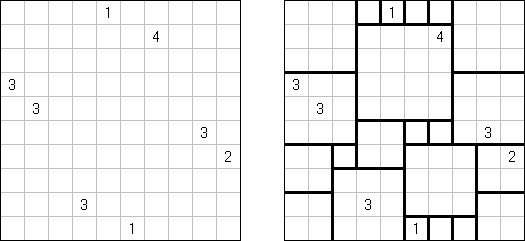
Shikaku ("Divide by Squares", "Divide by Box", "Number Area") é um quebra-cabeça lógico que representa uma rede retangular sem o tamanho padrão. Algumas células da rede contêm números. O objetivo é traçar as linhas dividindo a rede em regiões retangulares e quadrados de tal maneira que cada região contenha somente um número igual à área desta região.

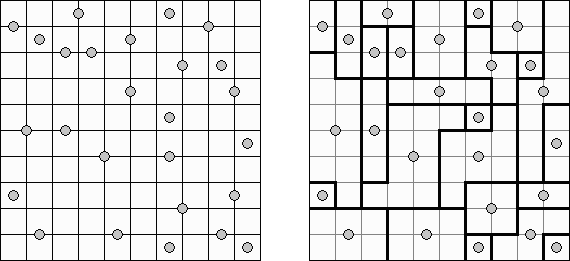
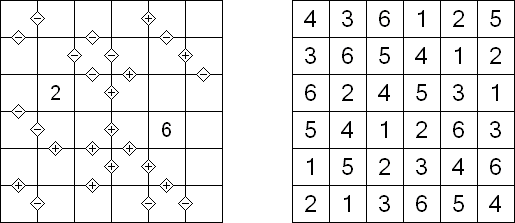
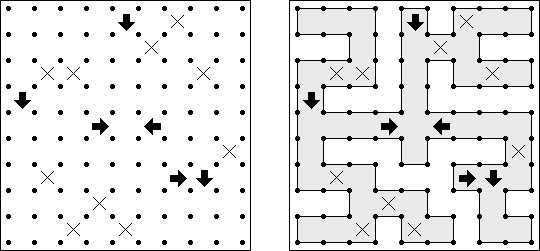
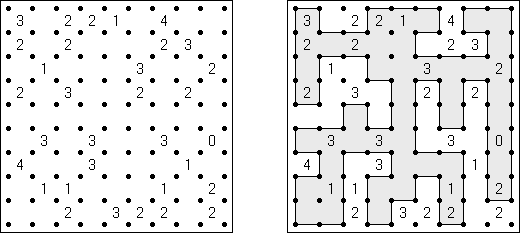
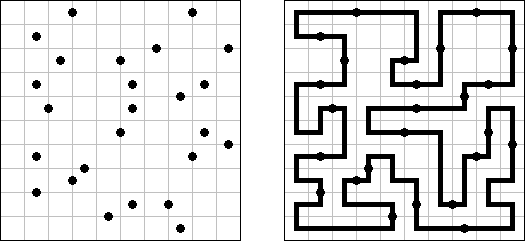
Galáxia ("Galaxies", "Tentai Show") é um problema composto de lógica e geometria. O quebra-cabeça é uma rede retangular com pontos. O objetivo é dividir a rede em regiões; cada região deve conter somente um ponto que seja o centro da simetria da região.

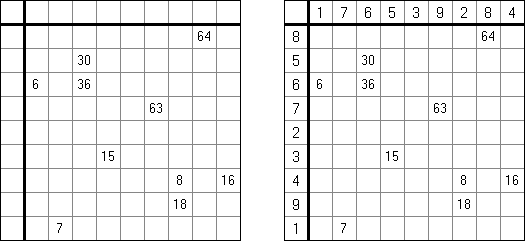
Arranha-céus ("Skyscrapers") é um tipo de quebra-cabeça lógico; o objetivo dele é preencher o quadrado com números de tal jeito que cada número seja utilizado em cada linha e cada coluna somente uma vez. O preenchimento deve ser realizado por meio dos números-chaves considerando o fato que dentro de cada célula exista uma casa com a quantidade de andares igual ao número na célula; os números fora do campo significam a quantidade das casas vistos na coluna ou linha correspondente (se olhar do lugar deste número).

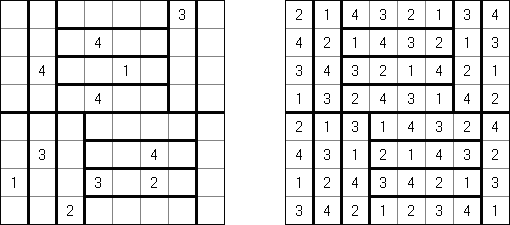
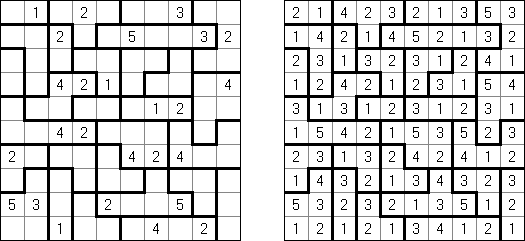
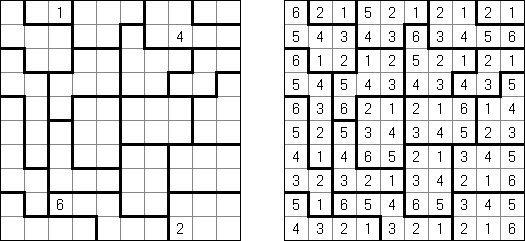
Hakyuu ("Ripple Effect", "Hakyuu Kouka", "Hakyukoka", "Seismic") é um tipo de quebra-cabeça lógico; o problema é composto de rede retangular dividida em blocos ("quartos") com números em alguns deles. O objetivo é preencher todas as células com números de tal maneira que cada bloco contenha os números de 1 até a quantidade das células no bloco. Caso a fileira das células ou coluna contenham dois números iguais, a quantidade das células entre eles deve ser maior ou igual aos estes números. Por exemplo, se uma coluna contém duas células com número 5, no mínimo cinco células com outros números devem estar entre elas.

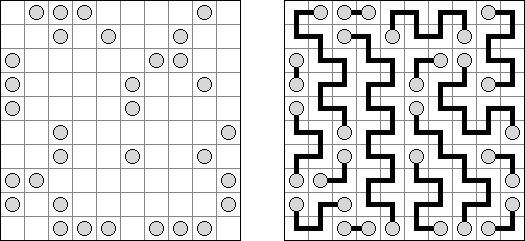
Grand Tour é um quebra-cabeça lógico cujo objetivo é traçar uma linha fechada através de todos os pontos da rede quadrada sem que ela se toque ou se atravesse. Para que o quebra-cabeça tenha uma solução única, alguns pontos já estão conectados por meio dos segmentos.

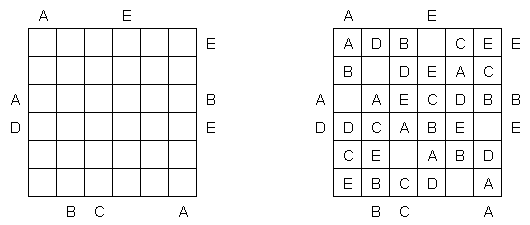
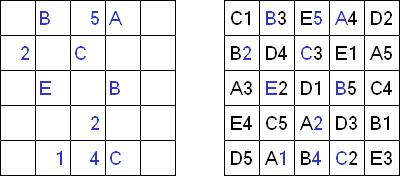
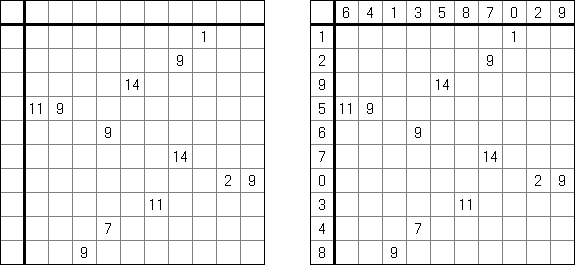
Simples como o ABC ("Easy as ABC", "ABC End View", "Last Man Standing") é um quebra-cabeça lógico de letras. O objetivo é preecher uma rede quadrada com as letras em latim (por exemplo, de A a E) de tal maneira que cada símbolo encontre-se somente uma vez em cada linha e cada coluna. Algumas células da rede podem estar vazias. A letra que está no limite da rede indica a letra que será encontrada primeira nesta linha (coluna).

Nuvens ("Clouds", "Rain Clouds", "Radar") é um tipo de quebra-cabeça "Batalha naval". O objetivo é dispor os retângulos ("nuvens") na rede da forma livre de tal maneira que eles não entrem em contato entre si, mesmo com os ângulos. Os números nos limites da rede indicam a quantidade das células ocupadas pelas nuvens. A quantidade e o tamanho das nuvens não são definidos; somente a informação que os lados dos retângulos têm o comprimento abaixo de dois é determinada.

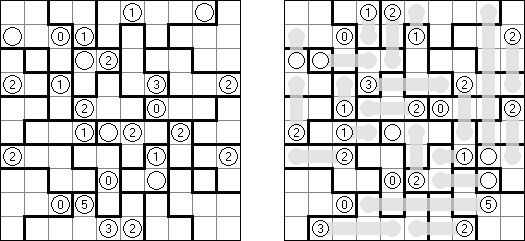
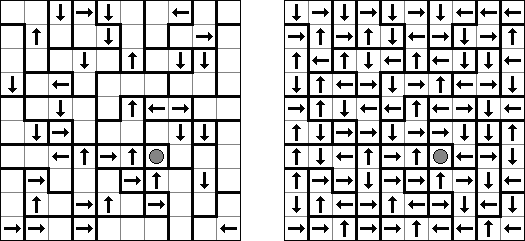
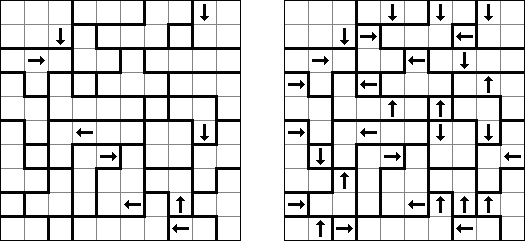
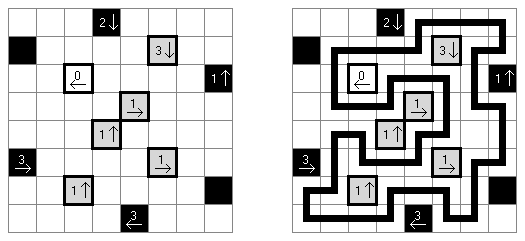
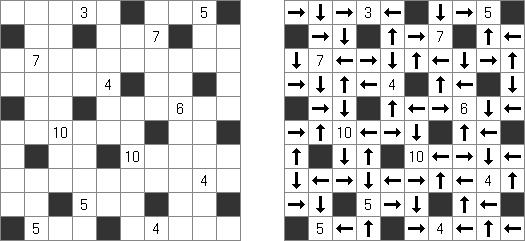
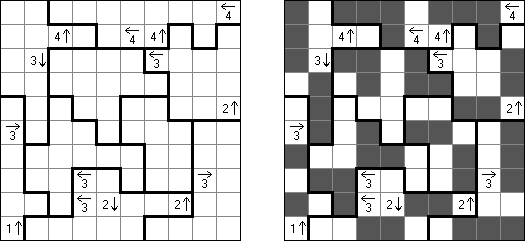
Yajilin ("Arrow Ring", "Straight and Arrow") é um quebra-cabeça lógico quadrado ou retangular. A tarefa contém as células com setas e números; essa informação é necessária para a disposição das células da cor preta pelo campo. O objetivo é desenhar um nó fechado que não se atravesse e que não passe através das células com setas ou das células pretas. The grid may contain gray cells that can not be part of the loop.

• Os números nas células indicam a quantidade das células pretas que estão em tal fileira ou em tal coluna e tal direção que a seta indica. As células com setas não são consideradas as células pretas.
• Caso a célula não contenha seta e não seja preta, ela deverá conter um segmento de nó.
• Os números nas células indicam o número exato das células pretas. Então, se uma célula da rede contém número "3" com seta indicando a esquerda, isso significa que três células pretas estão na fileira do lado esquerdo desta célula.
• As células pretas não podem entrar em contato entre si nas direções vertical ou horizontal.
• O campo pode conter as células pretas que não são indicados por nenhuma seta.

Campo minado ("Minesweeper", "Draga-minas") é um jogo conhecido por todos os usuários do sistema operacional Microsoft Windows. É necessário dispor as "minas" nas células livres utilizando as palavras-chaves. Cada palavra chave indica a quantidade das células vizinhas contendo minas. As minas são colocadas de tal maneira que cada célula contenha uma mina, e uma célula com número não contenha nenhuma.

Minesweeper Battleships ("Battlemines") combina as características de dois quebra-cabeças populares (Batalha naval e Campo minado). Deve colocar non campo os navios de tal maneira que não se toquem mesmo por ângulos. Em alguns quadrículos da grade estão os números. Estes números mostram o número de fragmentos de navios localizados em torno de uma determinada quadrículo (inclusive na diagonal).

Heyawake é um quebra-cabeça lógico, que é uma rede retangular sem o tamanho padrão dividido em blocos ("quartos)". Alguns blocos podem conter números; um número apresenta a quantidade das células pretas que um bloco deve conter. Caso o número no bloco seja ausente, tal bloco pode conter qualquer quantidade das células pretas.

• As células pretas não podem entrar em contato entre si nas direções vertical ou horizontal (somente no diagonal).
• As células brancas são ligadas entre si no vertical ou horizontal.
• Uma linha contínua das células brancas não pode atravessar mais de três "quartos".

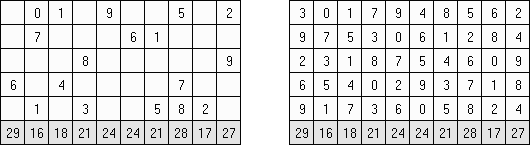
Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten") é uma rede retangular com a largura de 10 células. O objetivo é preencher a rede de tal maneira que cada fileira contenha números de 0 a 9. Os números nas colunas podem ser repetidos. O número debaixo da rede significa o valor sumário de todos os números na coluna. Os números que estão nas células vizinhas (mesmo se essas células entram em contato entre si somente no diagonal) podem ser diferentes.

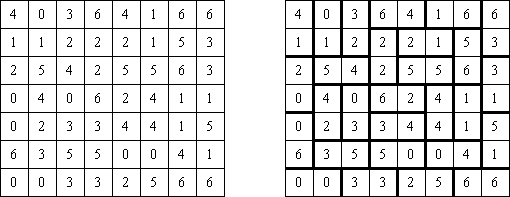
Cem ("Hundred") é composto de uma rede quadrada com números em cada célula. O objetivo é colocar os números adicionais de tal maneira que o valor sumário dos números em cada fileira e cada coluna seja igual a 100.

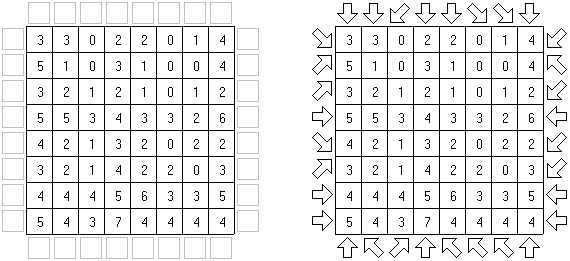
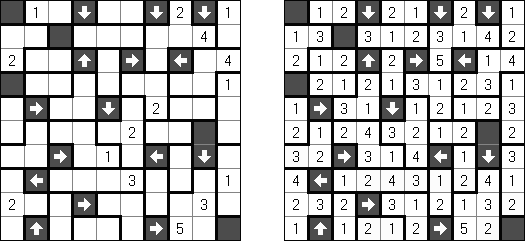
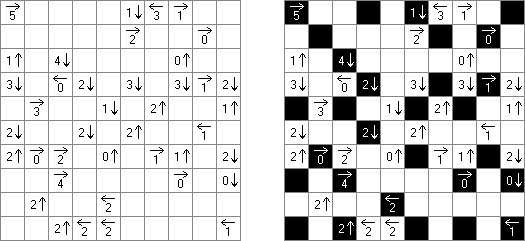
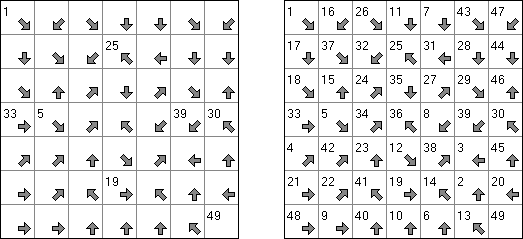
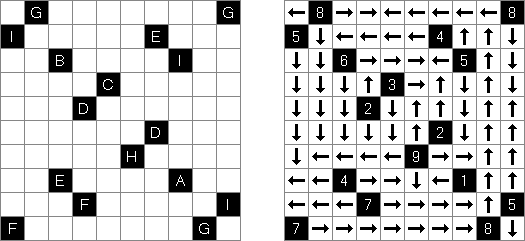
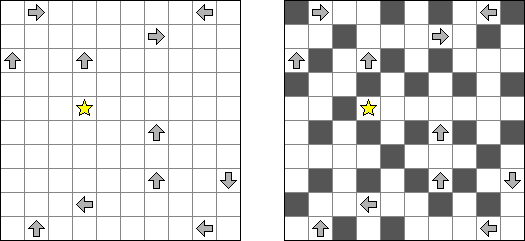
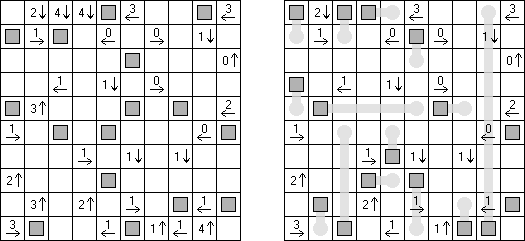
Flechas ("Arrows") é um tipo de quebra-cabeça lógico composto de uma rede retangular ou quadrada preenchida com números. O objetivo de quebra-cabeça é dispor as setas fora da rede. Cada seta indica para no mínimo uma célula com número. O número significa a quantidade das setas que indicam para esta célula.

Mathrax consiste em uma rede quadrada. O objectivo é preencher cada célula com números de 1 a N, onde N é o tamanho do lado do quebra-cabeça. Nenhum número pode aparecer duas vezes em qualquer linha ou coluna. Círculos com condições adicionais podem estar situados nas interseções das linhas dentro da rede.

• Um número e um sinal de operação matemática (adição, subtração, multiplicação, divisão) - um número é resultado de uma execução da operação com números nas células diagonalmente adjacentes.
• A letra "E" ("par") - todos os números em quatro células são pares.
• A letra "O" ("ímopar") - todos os números em quatro células são ímpares.

Str8ts ("Straights") é um quebra-cabeça lógico, inventado por Jeff Widderich (Canadá). É uma rede parcialmente dividida por células pretas em compartimentos. Cada compartimento, vertical ou horizontalmente, deve conter uma recta - um conjunto de números consecutivos, mas em qualquer ordem (por exemplo: 2-1-3-4). Nenhum número se pode repetir em alguma linha ou coluna. As pistas em células pretas eliminam esse número como uma opção em que linha e coluna, e não fazem parte de qualquer recta.

Procura Linhas ("Linesweeper") é jogado numa rede retangular. O objetivo é criar uma volta única contínua sem intersecções que ligue os centros das células. As células numeradas não podem ser atravessadas, o número na célula significa quantas das 8 células vizinhas devem conter alguma parte da via da solução. (Por exemplo, "0" significa que as 8 células vizinhas não podem ser atravessadas de algum modo).

Binairo ("Binary Puzzle", "Takuzu", "Tohu wa Vohu") é jogado numa rede quadrada ou rectangular. O objetivo é preencher a rede com dígitos "0" e "1" de acordo com as seguintes regras:

• O número dos dígitos "0" e "1" em cada linha e cada coluna é igual.
• Não mais de duas células em uma linha podem conter o mesmo número.
• Cada linha é única, e cada coluna é única.

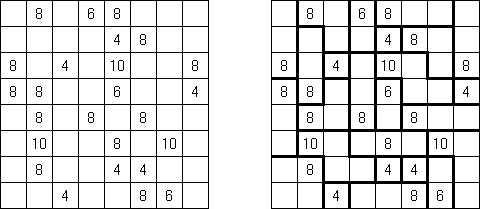
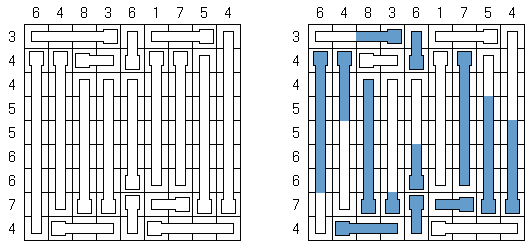
Paredes ("Walls") é um quebra-cabeça lógico inventado pelo japonês Naoki Inaba. Nos quadrículos brancos deve colocar as linhas horizontais e verticais de modo que o comprimento total de todos os "raios" que partem do quadrículo preto coincida com o número colocado em tal quadrículo.

Dominosa ("Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") é um quebra-cabeça lógico que usa dados de dominó. No campo se mostram apenas os números; você deve restaurar os límites entre os dados de dominó.

Patchwork ("Tatami") é um quebra-cabeça numa grade quadrada dividida em partes de igual tamanho ("quartos"). Você deve preencher todos os quartos com números de 1 ao que corresponde ao número de quadrículos na parte. Cada linha e cada coluna deve conter o mesmo número de cada dígito. Os quadrículos vizinhos em contacto horizontalmente ou verticalmente não devem conter os mesmos dígitos.

Em algumas tarefas desta variedade de quebra-cabeças se usam letras em vez de dígitos. Cross+A pode resolver os quebra-cabeças tanto com os dígitos como com as letras na tarefa.

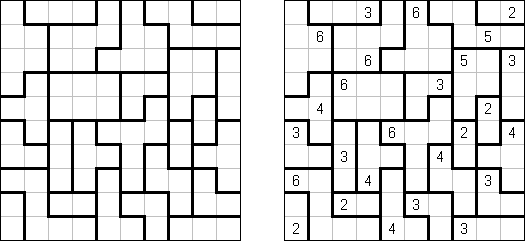
Cnossos ("Knossos", uma cidade antiga e um palácio na ilha de Creta, bem como a localização do labirinto no qual foi aprisionado o Minotauro) é uma grade quadrada ou rectangular, com dígitos em alguns quadrículos. Você deve dividir a grade em zonas ("quartos") para cada zona contiver um número. Este número deve ser igual ao comprimento do perímetro da zona.

Rekuto ("Recto") é um quebra-cabeça lógico de forma quadrada ou rectangular. Em alguns quadrículos da grade estão os números. Deve desenhar as linhas que dividam a rede em áreas rectangulares e quadradas para cada área contiver apenas um número igual à soma da largura e da altura da área.

Vizinhos ("Neighbours") é um quebra-cabeça lógico que representa uma grade de forma arbitrária. Em alguns quadrículos estão os números ou pontos de interrogação. A grade deve ser dividida em áreas com igual número de quadrículos. Cada área deve conter apenas um quadrículo com um número (ou um ponto de interrogação), este número indica quantas "vizinhas" deve ter tal área. Duas áreas são consideradas adjacentes se têm um límite comum. Se uma área contiver um quadrículo com um ponto de interrogação tal área pode ter qualquer número de "vizinhos".

Quatro ventos ("Four Winds", "Line Game") é um quebra-cabeça de lógica que representa uma grade quadrada ou rectangular, com quadrículos em preto e branco. É preciso desenhar linhas rectas que partam dos quadrículos pretos e passem por todos os quadrículos brancos. O número no quadrículo negro indica quantos quadrículos brancos são atravessados pela linha unida com o quadrículo preto. As linhas não devem se cruzar.

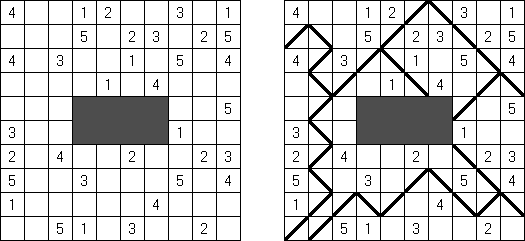
Shakashaka ("Proof of Quilt") é um quebra-cabeça de lógica de forma quadrada ou rectangular. O conjunto contém quadrículos a preto e branco, alguns quadrículos pretos podem ser numerados (0 a 4). É preciso colocar triângulos pretos nos quadrículos brancos de modo a formar áreas brancas rectangulares ou quadradas. Alguns quadrículos brancos podem ficar vazios. As áreas podem ser orientadas horizontalmente, verticalmente ou na diagonal. As áreas vizinhas de cor branca não devem ter lados comuns. A cifra no quadrículo preto indica quantos triângulos são contíguos com tal quadrículo.

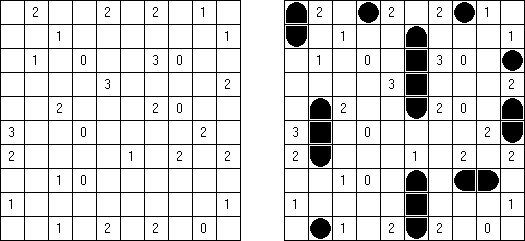
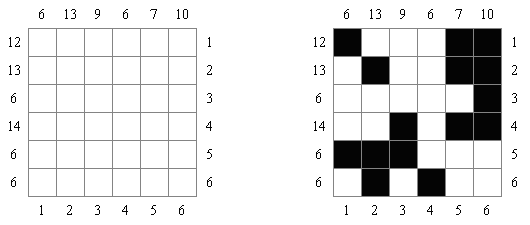
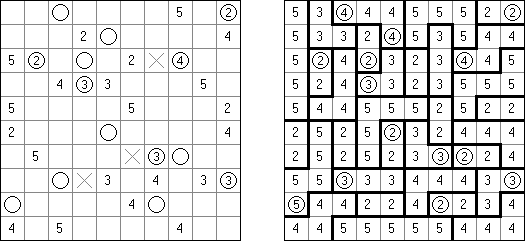
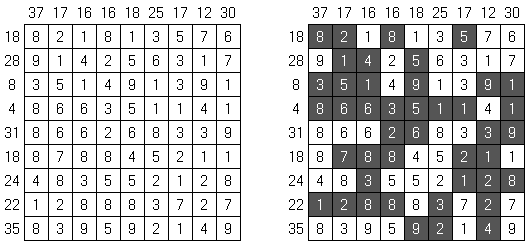
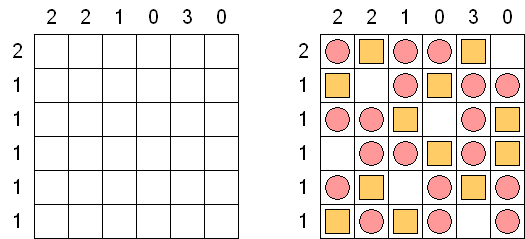
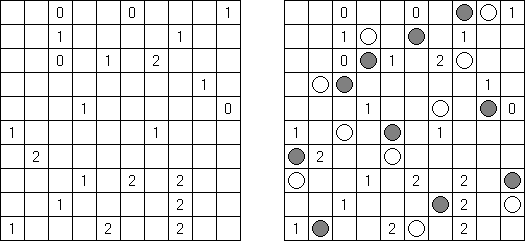
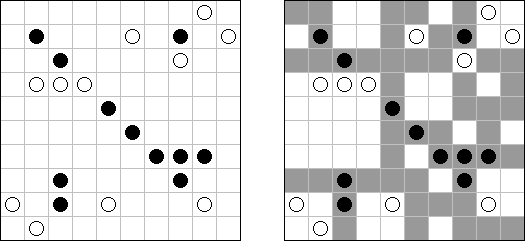
Kakurasu ("Index Sums") é um quebra-cabeça de lógica de forma quadrada ou rectangular, no qual é preciso colocar quadrículos em preto e branco. Os números à esquerda e por cima da grade representam a soma dos "pesos" dos quadrículos pretos nas correspondentes linhas e colunas. Os números à direita e debaixo da grade determina o "peso" de quadrículos pretas nas linhas e colunas correspondentes (o "peso" do quadrado preto na primeira linha ou na primeira coluna é 1, na segunda linha e segunda coluna 2, etc.).

Mochikoro ("Mochinuri") é uma grade quadrada ou rectangular, com numerous em alguns quadrículos. É preciso colocar os quadrículos em preto e branco de modo a formar "ilhas" rectangulares ou quadradas de quadrículos brancos.

• Uma "ilha" branca não pode conter mais de um quadrículo numerado; o número indica quantos quadrículos brancos pertencem a tal área.
• Algumas "ilhas" não contêm quadrículos com números.
• As áreas brancas não podem ter lados contiguous, mas todas as "ilhas" brancas se relacionam entre si na diagonal.
• A grade não deve conter algum quadrado 2 x 2 que consista apenas de quadrículos pretos.

Portas ("Seethrough", "Doors", "Open Office") é um quebra-cabeça de lógica de forma quadrada ou rectangular, onde cada quadrículo representa um "quarto". É preciso fechar ou abrir as "portas" entre as peças. Uma porta aberta permite ver de quarto em quarto ou várias peças de lado a lado. O número no quadrículo indica quantos quartos podem ser vistos a partir deste quarto, excepto o mesmo quarto. Não deve haver partes isoladas da grade, isto é, a partir de qualquer quarto se pode entrar em qualquer quarto.

Faróis ("Lighthouses") é um quebra-cabeça de lógica com quadrados pretos numerados ("faróis"). O número indica quantos navios são iluminados pelo farol. O farol ilumina os navios alinhados, mesmo se entre o farol e os navios há outros navios ou faróis. Cada navio é iluminado por, pelo menos, um farol. Os navios são colocados de tal maneira que não entram em contacto com os faróis ou entre si, inclusive diagonalmente.

Lighthouse Battleships:

Tapa foi inventado por Serkan Yurekli da Turquia. O quebra-cabeças é uma grade quadrada ou rectangular que consiste de quadrículos brancos. Precisa cobrir com tinta preta alguns quadrículos conforme as seguintes regras:

• Todos os quadrículos pretos deveriam se tocar na vertical ou na horizontal.
• Não deve haver grupos de quadrículos de 2 x 2 que consistam só de quadrículos pretos.
• Alguns quadrículos contêm números ou pontos de interrogação, tais quadrículos ficam sempre brancos.
• Cada número representa uma banda contínua de quadrículos pretos em torno dum quadrículo branco com tal número; dois desses grupos de quadrículos pretos devem ser separados por pelo menos um quadrículo branco.
• O ponto de interrogação representa qualquer número maior que zero.
• As posições dos números ou a ordem da sua colocação dentro dum quadrículo não têm importância.

Fobidoshi ("Forbidden Four") é um quebra-cabeça de lógica inventado por Naoki Inaba do Japão. O quebra-cabeça é uma grade quadrada ou rectangular, em alguns quadrículos estão colocados os círculos. É preciso colocar os círculos nos quadrículos vazios de modo que eles se toquem horizontalmente ou verticalmente. Não deve haver quatro círculos consecutivos em horizontal ou em vertical.

Ilha ("Island", "Tents Island", "Airando") é um quebra-cabeça lógico inventado pelo japonês Naoki Inaba. O quebra-cabeça tem a forma de uma grade em alguns dos quadrículos da qual estão os números. É preciso pintar os quadrículos da cor preta para que os quadrículos restantes em branco formem uma única ilha. Os quadrículos com números fazem parte da ilha. O número mostra quantos quadrículos brancos sem números podem ser obtidos movendo-se pela superfície da ilha do quadrículo com o número horizontalmente e verticalmente (até que outro quadrículo com número bloqueie o movimento).

Domínio ("Dominion") é uma grade, em alguns quadrículos da qual estão as letras. É preciso pintar alguns quadrículos da cor preta observando as seguintes regras:

• Os quadrículos pretos podem ser adicionados no campo apenas em pares, isto é, cada dois novos quadrados pretos se devem tocar na horizontal ou na vertical (tais pares de quadrículos são chamados "dominós").
• Os dominós podem entrar em contacto entre si apenas na diagonal.
• Os quadrículos com letras devem ficar brancas.
• Os quadrículos pretos dividem o campo em diferentes áreas brancas. Dentro de uma área todos os quadrículos brancos estão em contacto uns com os outros horizontalmente ou verticalmente.
• Os quadrículos com a mesma letra pertencem à mesma área branca.
• Não pode haver alguma área branca sem quadrículo com letra.

Tren é um quebra-cabeça lógico inventado por Shinichi Aoki do Japão. O nome japonês do problema lógico pode ser traduzido como "estacionamento" (cada unidade é um carro, e toda a grade é um parque de estacionamento). O quebra-cabeça tem aforma de uma grade quadrada ou rectangular, em alguns quadrículos estão números. Na grade devem ser colocados blocos de 1 x 2 ou 1 x 3. Cada número deverá ser parte de um único bloco. Este número indica por quantos quadrículos se pode mover o bloco. O bloco pode apenas ser movido na direcção do lado curto.

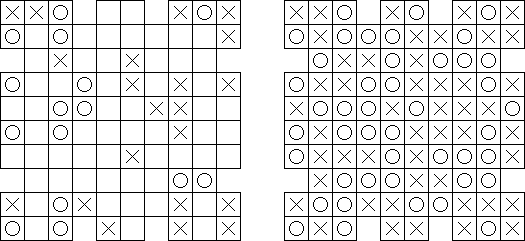
Três em linha ("No Four in a Row") é uma retícula de qualquer forma. Em certos campos da retícula estão colocados "X" ou "O". Deve preencher os campos restantes para que horizontalmente, verticalmente ou diagonalmente não haja mais de três sinais idênticos um após outro.

Corral ("Bag", "Cave") é uma retícula quadrada ou retangular, com números em alguns quadrículos. O objetivo é traçar uma linha fechada em torno de todos os números. O número indica quantos quadrículos podem ser vistos a partir desse quadrículo horizontalmente e verticalmente dentro da linha fechada, incluindo a mesma quadrícula.

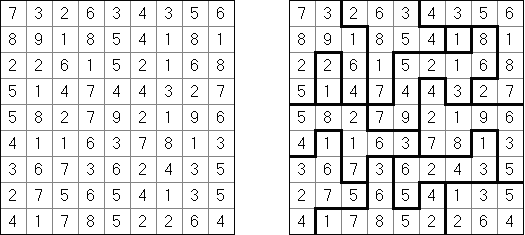
Cuatro campos ("Foseruzu", "Four Cells") é um quebra-cabeça lógico que representa uma retícula quadrada ou rectangular com números em certos campos. Você tem que dividir a retícula em blocos de 4 campos. O número indica quantos lados do campo contêm elementos de limites entre blocos (o limite exterior do campo também incluído). Um bloco pode conter qualquer quantidade de números (ou não conter algum).

Cinco campos ("Faibuseruzu", "Five Cells", "Solomon's Keep"): a retícula está dividida um blocos de 5 campos.

Sutoreto ("Sutoretokurosu", nome inglês "Straight Cross" alterada pela pronúncia japonesa) é um jogo de lógica inventado por Naoki Inaba do Japão. O jogo representa uma retícula rectangular ou quadrada com campos brancos ou pretos. Certos campos brancos têm números. Você tem que preencher com números os campos brancos restantes para que entre os campos pretos horizontalmente e verticalmente se formem conjuntos de números consecutivos, mas não necessariamente seguidos (por exemplo, 2-3-4 ou 5-4-7-6).

Renban é uma quadrícula dividida em áreas de forma e tamanho livres. Você tem que preencher a quadrícula com números de modo que cada número se encontre apenas uma vez em cada linha, cada coluna e cada bloco. Todos os números de área são uma série de números consecutivos, mas não necessariamente por ordem crescente ou descrescente (por exemplo, 5-3-4).

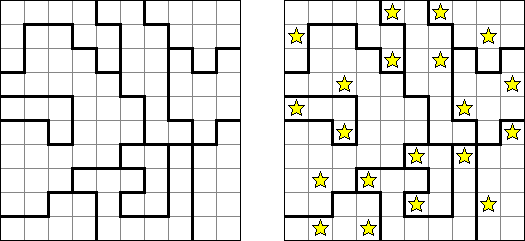
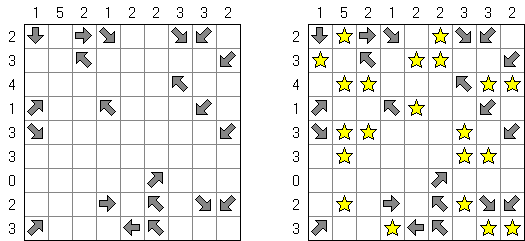
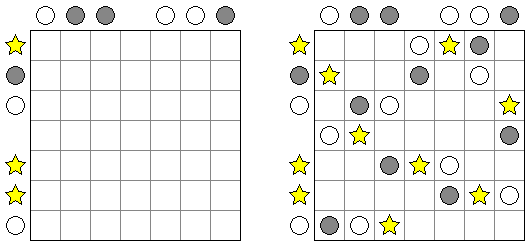
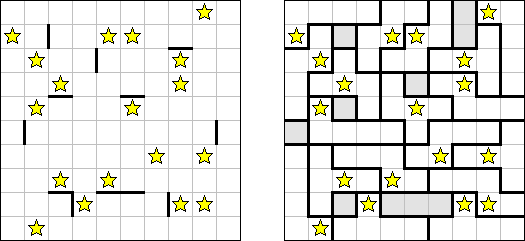
Buraitoraito (nome inglês "Bright Light" alterado pela pronúncia japonesa) é um quebra-cabeça inventado por Naoki Inaba do Japão. Representa uma retícula quadrada ou rectangular com campos brancos e pretos. Você tem que colocar estrelas nos campos brancos de modo que cada número num campo preto corresponda ao número de estrelas visíveis a partir do campo na horizontal e na vertical. A "visão" se estende até atingir a borda do campo ou tropeçar em outro campo preto.

Irasuto (nome inglês "Illustration" alterado pela pronúncia japonesa) é um quebra-cabeça lógico inventado por Naoki Inaba do Japão. O jogo representa uma grade retangular ou quadrada com com casas pretas e brancas. Certas casas estão sem números. Você tem que colocar as casas brancas e pretas observado as seguintes regras:

• O número numa casa branca indica quantas casas brancas "se vem" desde a casa verticalmente e horizontalmente. "O olhar" se estende até encontrar uma casa preta ou outra casa branca com número.
• O número numa casa preta indica quantas casas pretas "se vem" desde a casa verticalmente e horizontalmente. "O olhar" se estende até encontrar uma casa branca ou outra casa preta com número.

Suguru ("Number Blocks") é um quebra-cabeça de lógica inventado por Naoki Inaba do Japão. É uma grade quadrada ou retangular dividida em áreas. Você tem que preencher todas as casas com números de modo que cada área contenha números de 1 até o número de casas na área. As casas com números iguais não se podem tocar na horizontal, na vertical ou na diagonal.

Trinudo é um quebra-cabeça de lógica de forma quadrada ou retangular. Em ceertas casas da grade há números. Você tem que dividir a quadrícula em blocos de uma, duas ou três casas. Os blocos do mesmo tamanho não se devem tocar horizontalmente ou verticalmente. Cada número indica quantas casas contém o bloco ao qual pertence o número.

Creek ("Kuriku") é um quebra-cabeça de lógica ou representa uma grade quadrada ou retangular, nas interseções das linhas podem ser colocados círculos com números de 0 a 4. O número indica quantas casas pretas são adjacentes ao círculo. Você deve colocar as casas pretas e brancas de modo que todas as casas brancas se toquem na vertical ou na horizontal.

Gappy é um quebra-cabeça lógico que representa uma grade quadrada. Deve colocar os quadrados pretos na grade de modo que cada linha e cada coluna tenha duas células pretas. As células pretas não se podem tocar, nem mesmo na diagonal. Os números fora da grade denotam o número de células brancas entre as células pretas na linha ou coluna.

Norinori é uma espécie de quebra-cabeça lógico. Representa uma grade rectangular ou quadrada dividida em áreas de forma livre. Deve pintar de preto duas células em cada área. As células pretas pintadas devem formar blocos de tamanho 2x1 ou 1x2 (dominó), independentemente dos límites das áreas. Dois blocos de cor preta não se podem tocar lateralmente (mas se podem tocar por ângulos).

Yonmasu ("Yonmasubunkatsu") é um quebra-cabeça lógico inventado pelo japonês Naoki Inaba. Representa uma grade de forma quadrada ou rectangular. Algumas células contêm círculos. A grade deve ser dividida em áreas de quatro células, cada área contendo um círculo.

Tijolos ("Bricks") é uma espécie de quebra-cabeça lógico. Vocé deve preencher a quadrícula com números de modo que em cada linha e cada coluna não se repitam. Em cada tijolo há um dígito: um par e o outro ímpar.

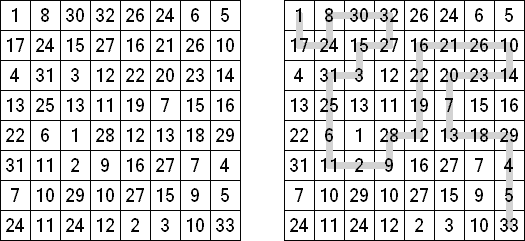
Cadeia de números ("Number Chain") é um quebra-cabeça com números inventado por Leonid Mochalov da Rússia. Trata-se de uma quadrícula retangular ou quadrada, cada célula da qual contém um número. No ângulo superior esquerdo da quadrícula está o número 1, no ângulo inferior direito está N; as quadrículas restantes contêm números arbitrários de 1 a N. Deve abrir o caminho a partir do ângulo superior esquerdo da quadrícula para o ângulo inferior direito de modo que a linha quebrada atravesse N células com números que não se repetem.

Kapetto ("Settokapetto" - nome inglês "Set Carpets" deformado pela pronúncia japonesa) é um quebra-cabeça lógico inventado pelo japonês Naoki Inaba. Representa uma grade rectangular ou quadrada, algumas células contêm números. Deve colocar as áreas rectangulares de grade de modo que cada área contenha um número. O número refere-se ao tamanho da área. A grade pode conter células que não pertencem a nenhuma área.

Renkatsu é um quebra-cabeça de lógica inventado por Naoki Inaba do Japão. É uma grade de forma quadrada ou retangular completamente preenchida com números. Você deve dividir a grade em áreas de modo que cada área contenha números de 1 a N, em que N é o tamanho da área.

Eulero ("Quadrado greco-latino") é um quebra-cabeças com letras e números. Você deve preencher com símbolos a quadrícula quadrada de modo que sejam cumpridas as seguintes condições:

• Em cada célula há uma letra e um dígito.
• Em cada linha e em cada coluna de cada letra e cada dígito ocorrem apenas uma vez.
• Cada combinação de letras e números ocorre no quadrado apenas uma vez.

Anraikumozaiku (pronúncia da frase inglesa "Unlike Mosaic" deformada pela pronúncia japonesa) é um quebra-cabeça lógico criado por Naoki Inaba do Japão. É uma quadrícula retangular ou quadrada, algumas células da qual contêm círculos. A quadrícula deve ser dividida em regiões de uma forma retangular de modo que em cada região se encontre um círculo. As células negros não pertencem a nenhuma das regiões. As regiões que contêm o mesmo número de células não se podem tocar na vertical ou na horizontal.

Kurotto ("blocos negros" em japonês) é uma espécie de quebra-cabeça lógico. Trata-se de uma quadrícula retangular ou quadrada, algumas células da qual contêm círculos (em branco ou com números). Deve colocar as células brancas e pretas observando as seguintes condições:

• Uma célula com círculo não pode ser pintada da cor preta.
• As células pretas formam regiões em que as células se tocam na horizontal e na vertical.
• O número dentro do círculo é igual à superfície de todas as regiões das células pretas contíguas horizontalmente e verticalmente com a célula correspondente.
• Se o círculo não contém números, tal célula pode tocar regiões de células pretas de qualquer tamanho.

Tasukuea (do japonês, literalmente "encontra quadrados") é um tipo de quebra-cabeças lógico. É jogado em uma grade quadrada ou retangular com números ou pontos de interrogação em algumas células. O objetivo é enegrecer algumas células da grade de acordo com as seguintes regras:

• As células com números ou pontos de interrogação não podem ser enegrecidas.
• As células pretas formam áreas quadradas.
• As áreas quadradas não devem ser ortogonalmente adjacentes.
• O número no círculo indica o número total de células pretas em áreas ortogonalmente adjacentes à célula numerada.
• Cada célula com ponto de interrogação deve ter pelo menos uma célula preta adjacente.
• Todas as células brancas devem ser conectadas horizontalmente ou verticalmente formando um campo único.

A batalha estelar ("Star Battle") é um quebra-cabeça que consiste em uma grade quadrada dividida em regiões de qualquer forma. O objetivo é colocar as “estrelas” (círculos) em algumas células na grade para que cada linha, coluna e região contenha o mesmo número de “estrelas”. As “estrelas” não podem ser colocadas em células adjacentes, nem mesmo em diagonal.

Araf (do turco, literalmente "purgatório", nome japonês original "Aidabeya") é um quebra-cabeça de lógica. É jogado em uma grade retangular ou quadrada, com algumas células numeradas. O objetivo é dividir a grade em regiões de modo que cada região contenha exatamente dois números. Cada região deve ter uma área de valor intermédio entre esses dois números. Por exemplo, se a região contiver 2 e 5, a área da região deve ser igual a três ou quatro células.

Kabingurodo (nome inglês "Curving Road" deformado pela pronúncia japonesa) é um quebra-cabeça lógico inventado pelo japonês Naoki Inaba. Representa uma grade rectangular ou quadrada em que algumas células contêm círculos. Deve colocar as células pretas na grade observando as seguintes regras:

• As células com círculos não podem ser pretas.
• As células pretas não se podem tocar na horizontal e na vertical, mas se podem tocar na diagonal.
• Todas as células brancas formam um único campo branco, i.e. se tocam na vertical ou na horizontal.
• Qualquer rota que se pode abrir pelas células brancas de um círlulo para outro deve girar ao menos duas vezes.

Os termômetros ("Thermometers") são um tipo de quebra-cabeça de lógica. Por cima da grade rectangular ou quadrada estão colocados os termômetros que estão vazios, parcialmente cheios ou completamente preenchidos. Os números no exterior indicam quantas células estão preenchidos nessa linha ou coluna. Cada termômetro é preenchido a partir da base (parte alargada), em direção ao topo, independentemente da orientação real do termômetro.

Serpente ("Snake", "Tunnel") é um tipo de quebra-cabeça lógico. É jogado em uma grade retangular ou quadrada, onde estão marcados os pontos inicial e final da “serpente”. A tarefa é enegrecer certas células para que se forme uma linha contínua entre os pontos. A “serpent” nunca se toca, nem mesmo em diagonal. Os números fora da grade mostram quantas células devem ser enegrecidas na linha ou coluna correspondente.

Peintoeria ("Paint Area") é um quebra-cabeça de lógica. O quebra-cabeça consiste em uma grade retangular dividida em regiões de qualquer forma. O objetivo é enegrecer algumas células para que todas as células pretas se toquem ortogonalmente. As células da mesmas região devem ser da mesma cor. Não deve haver grupos de células 2 x 2 da mesma cor. O número dentro da célula indica quantas células pretas são ortogonalmente adjacentes a esta célula.

Irupu ("I-Loop") é um quebra-cabeça de lógica inventado por Naoki Inaba (Japão). Uma grade retangular ou quadrada contém círculos em algumas células. O objetivo é colocar na grade alguns blocos de tamanho de 1 x 3 ou 3 x 1. Cada bloco contém um círculo e deve ser ortogonalmente adjacente a exatamente dois outros blocos. Todas as células de bloco formam uma região única.

Sashigane (do japonês, literalmente "esquadro do carpinteiro") é um tipo de quebra-cabeça lógico quadrado ou retangular. Algumas células podem conter círculos (com ou sem números) ou flechas. O objetivo é dividir a grade em regiões em forma de L. As duas "pernas" de uma região devem ser exatamente da largura de uma célula. O círculo representa uma célula na qual uma L deve se dobrar (a grade contém círculos não para todas as regiões). O número no círculo indica quantas células tem a região. A flecha marca o fim da "perna" da L; A flecha aponta para a célula em que a L se dobra.

Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

Chocona ("Chocolate") consiste em uma grade quadrada ou retangular dividida em regiões de diferentes formas. O objetivo é enegrecer algumas células da grade para formar regiões pretas retangulares, independentemente das bordas da região. As regiões pretas não devem ser ortogonalmente adjacentes. Uma célula com um número indica quantas células na região podem ser enegrecidas. Numa região sem número pode ser enegrecido qualquer número de células.

Diferentes vizinhos ("Different Neighbours") é um quebra-cabeça lógico que consiste em uma grade quadrada ou retangular dividida em regiões de diferentes formas. Certas regiões estão numeradas. O objetivo é colocar um número de 1 a 4 no resto das regiões, de modo que nenhuma região que se toque (mesmo na diagonal) compartilhe o mesmo dígito.

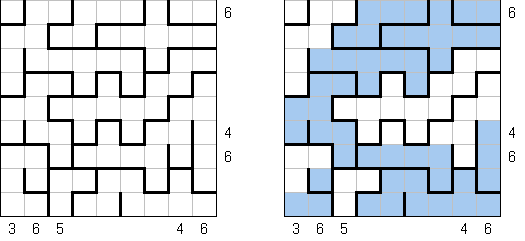
LITS ("Nuruomino") é um quebra-cabeça de lógica que consiste em uma grade retangular ou quadrada de qualquer tamanho dividida em regiões de diferentes formas. O objetivo é colocar em cada região exatamente uma figura de quatro células conectadas, para formar um tetromino que pode ser de quarto tipos: L, I, T ou S.

Os tetrominos podem ser girados ou espelhados. Quando dois tetrominos em regiões adjacentes compartilham uma borda, eles não devem ser do mesmo tipo (mas podem se tocar diagonalmente). Todos os tetrominoes devem formar uma área ortogonalmente contígua. Não deve haver tetrominos de 2 x 2 que consistem só das células pertencentes aos tetrominos.

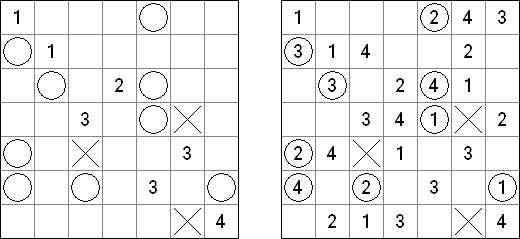
Nanbaboru ("Number Ball") é um quebra-cabeça que consiste em uma grade quadrada inventado por Naoki Inaba (Japão). O objetivo é preencher algumas células com números do intervalo dado. Nenhum número pode aparecer duas vezes em qualquer linha ou coluna. Uma célula com um círculo deve conter um número; uma célula com uma cruz não pode conter um número.

Tairupeinto ("Tile Paint", "Crazy Pavement") é um quebra-cabeça que consiste em uma grade quadrada ou retangular dividida em regiões de diferentes formas. O objetivo é enegrecer algumas células para que cada região seja completamente enegrecida ou completamente branca. Os números externos indicão o total das células enegrecidas na linha ou na coluna.

Yin-Yang é um quebra-cabeça que consiste em uma grade quadrada ou retangular com círculos brancos e pretos em algumas células. O objetivo é colocar um círculo preto ou branco em cada célula vazia para que todos os círculos da mesma cor estejam conectados entre si, verticalmente ou horizontalmente. Além disso, não deve haver um grupo de círculos de 2 x 2 que contenha círculos da mesma cor.

Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.

Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.

Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.

Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.

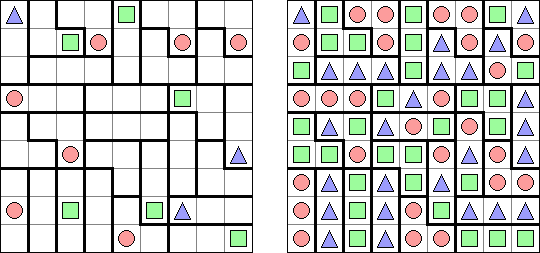
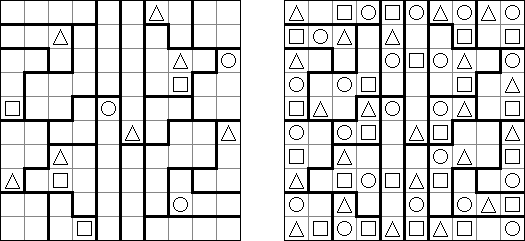
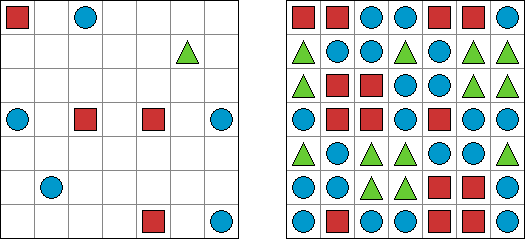
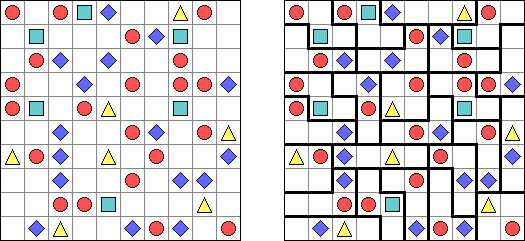
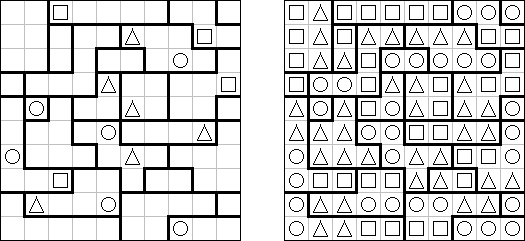
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.

Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.

Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.

Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.

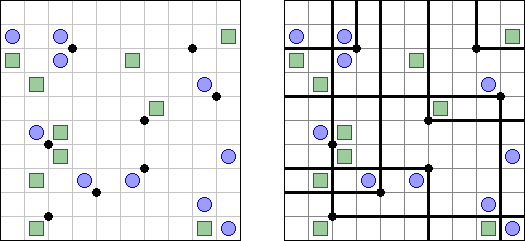
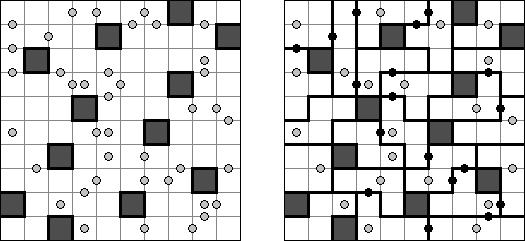
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.

Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.

Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.

Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.

Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.

Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:

• White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle.
• Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.

Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.

Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.

Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.

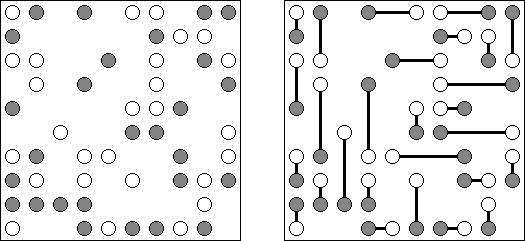
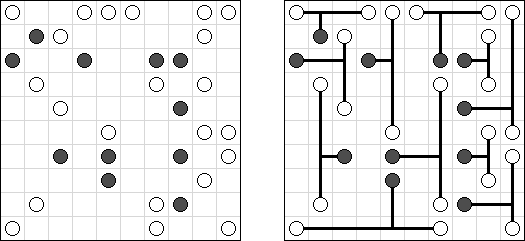
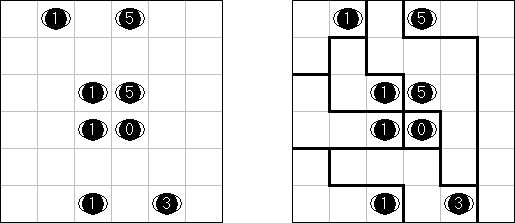
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.

Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.

Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.

Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.

Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:

• Each region contains exactly one arrow.
• Each two arrows are paired, they point to each other. There are no unpaired arrows.
• Two regions with paired arrows must not be horizontally or vertically adjacent.
• Between two paired arrows no other arrow must be placed.

Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.

Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.

Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.

Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• The black cells divide the grid in areas of white cells. Each area contains one cell with a number.
• Each area must have the same number of white cells as the number it contains (including the numbered cell).
• Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide.
• If two stripes are connected diagonally, the length of the stripes must be different.

Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.

Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.

Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.

Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells).
• Two black cells must not be orthogonally adjacent.
• All of the white cells must be connected.

Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.

Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:

• Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake").
• Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed.
• Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached.
• The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.

Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.

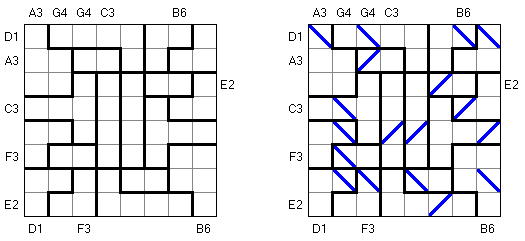
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.

Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.

Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• Two regions with the same amount of black cells must not be orthogonally adjacent.
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.

Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:

• Black cells must not be orthogonally connected.
• A cell with a number may be blacken.
• All the white cells must form an orthogonally continuous area.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.
• Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.

Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:

• A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally.
• A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all.
• A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells.
• Two snakes of the same length must not be orthogonally adjacent.
• A cell with a cross cannot be an end of a snake.

Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:

• Start at any stone.
• When a stone is encountered, it is picked up.
• When a stone is picked up, the direction can be changed.
• It is not allowed to reverse the direction.

Water Fun ("Aquarium") is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.

Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.

Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.

Santoitchi ("San to itchi"; from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• All white cells must be divided on regions having the size of exactly three cells.
• Two black cells must not be orthogonally adjacent.
• Each region contains a number.
• A number indicates how many black cells share an edge with that region.

Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.

Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.

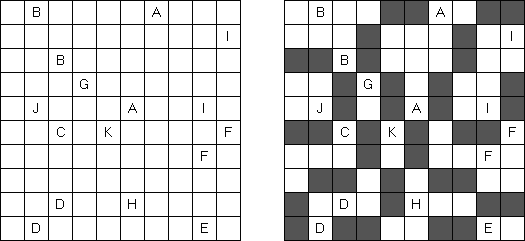
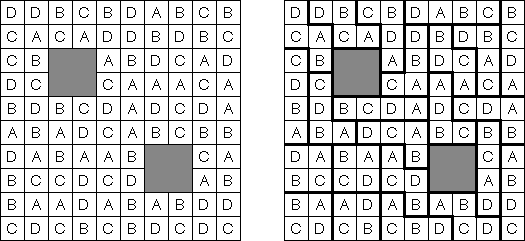
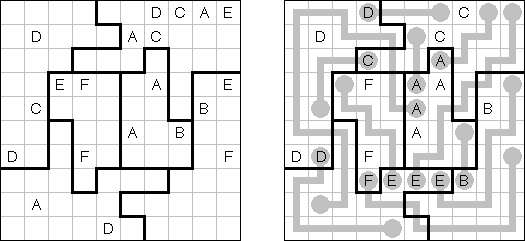
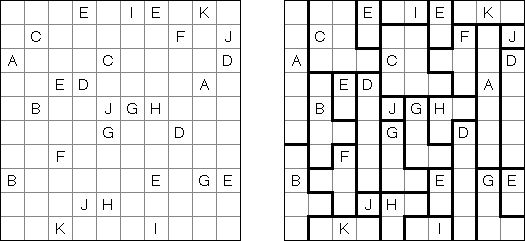
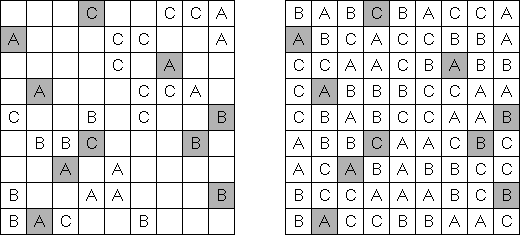
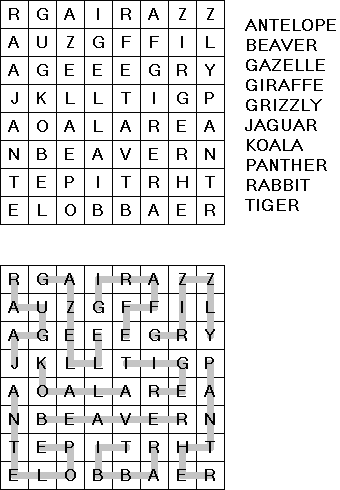
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.

Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.

EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.

Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.

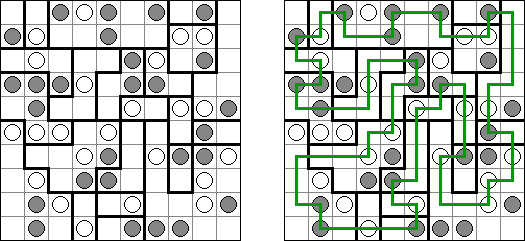
Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.

Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.

Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:

• All black cells in a region must be connected horizontally or vertically.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• If all stones "fall down", they must cover exactly the bottom half of the grid.

Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.

Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.

Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.

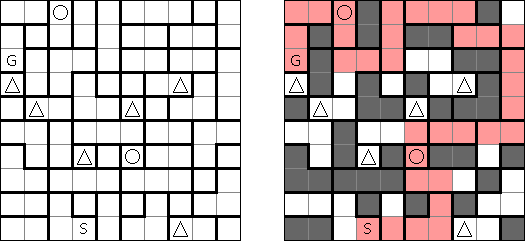
Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:

• Cells with letters, circles or triangles are always white.
• White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide.
• A path from S to G includes all cells with circles and no cells with triangles.
• No 2 x 2 cell area within the grid can have the same color.
• All white cells must form an orthogonally continuous area.
• White cells must not form a loop.

Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:

• All black cells create a single connected group.
• No 2 x 2 cell area within the grid can contain all black cells.
• Numbered cells must not be black.
• Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.

Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.

Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:

• Each region contains one black circle.
• Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.

Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.

Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.

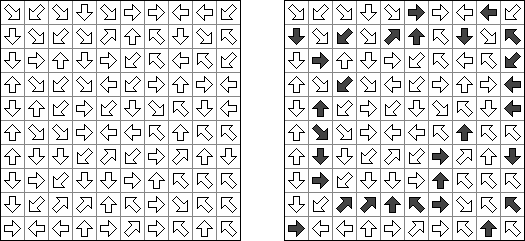
Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.

Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.

Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)

Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.

Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.

Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.

Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:

• Black cells form an area of square shape.
• No black areas touch each other horizontally or vertically (only diagonally).
• Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size.
• Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.

Golem Grad (an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:

• The black cells divide the grid into areas of white cells ("islands"), each containing at most one number.
• Two islands may not be connected.
• The island must have the same number of white cells as the number it contains.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the black color.
• All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid.
• Snakes must not cross each other.

Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:

• No two horizontally, vertically or diagonally adjacent cells contain a digit.
• The numbers across the top and down the left equal the row and column totals for the cells with numbers.
• The numbers across the bottom and down the right are the sums of numbers in the rows and columns.

Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.

Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• White cells form a path exactly one cell wide.
• Cells with circles are always white.
• A cell with a circle must have exactly one white cell adjacent to its side.
• A white cell without a circle must have at least two orthogonally adjacent white cells.
• A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself.
• All the white cells must be connected horizontally or vertically.
• No 2 x 2 cell area within the grid can have the same color.

Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:

• The white circle indicates that the sun is closer to the star than the moon.
• The black circle indicates that the moon is closer to the star than the sun.
• The star outside the grid indicates that the circles are at equal distance from the star in that row or column.

Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.

Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.

Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.

Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.

Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)

Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.

Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.

Nuraf ("Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells divide the grid into areas of white cells ("islands").
• Cells with numbers are always white.
• Two islands may not be connected.
• All of the black cells must be connected.
• No 2 x 2 cell area within the grid can have the black color.
• Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.

Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.

Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.

• The same arrows cannot be placed in adjacent cells.
• Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached.
• A cell with a number indicates a total number of arrows that leads to this cell.

Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.

Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.

Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.

Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)

Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.

Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.

Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.

Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.

Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.

Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.

Meandering Numbers (also known as "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)

Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.

Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.

From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.

Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.

Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.

Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.

Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)

Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.

Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).

Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.

Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).

Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.

Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.

Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.

Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.

Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.

Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.

SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.

Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border.
• A cell with a number indicates how many cells in the region must be blackened.
• No two black areas may share an edge.

Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.

Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.

Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.

Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.

Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.

Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.

Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:

• The black cells form "islands". No two islands may share an edge; islands may be connected through their corners.
• If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island).
• All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners.
• If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).

Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.

Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All white cells form one orthogonally connected area.
• A line of connected white cells cannot go through two or more region borders.

Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.

Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.

Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally).
• A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer.
• Each block contains exactly one number or a question mark.
• All blocks form "chains". A chain is a group of two or more blocks, connected through their corners.
• Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.

Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened.
• Blackened cells should not share an edge.
• All the white cells must be connected inside a region (it's possible for a region to have no white cells).
• If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions.
• All the white cells must form an orthogonally continuous area.

Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its N^th entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.

Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.

Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.

Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected horizontally or vertically (they form a "block").
• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any amount of cells may be blackened (all cells may stay white).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All blocks of black cells must be connected to each other through their corners.
• No 2 x 2 cell area within the grid can contain all black cells.

Kazoku ("Kazoku shashin"; from Japanese, literally "family photo") is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.

Tontonbeya (from Japanese, literally "gambler") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.

Contexto ("Context") is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:

• All the white cells must be connected horizontally or vertically.
• A cell with a number can be blacken. Two black cells must not be orthogonally adjacent.
• The number in a white cell indicates the number of orthogonally adjacent black cells.
• The number in a black cell indicates the number of diagonally adjacent black cells.

Word Finder ("Word Search", "Word Seek", "Word Sleuth", "Mystery Word") é uma grade com letras de forma quadrada ou rectangular. É preciso achar as palavras escondidas na grade com letras. As palavras são lidas numa linha quebrada, a linha só pode dobrar em ângulos rectos. Cada letra pode ser usada apenas numa única palavra.

Para criar o quebra-cabeça, você deve especificar uma lista de palavras. Também pode especificar uma palavra-chave composta das letras que ficam depois de resolver o quebra-cabeça.

Nove letras ("Nine Letters") é uma variedade do quebra-cabeça Word Finder. É uma quadrícula com letras, dividida em regiões de tamanho 3 x 3. Deve encontrar palavras de 9 letras escondidas dentro de cada região.

Teia de aranha ("Spider Web") consiste em círculos ligados por linhas entre si. Nos círculos estão colocadas letras. Deve encontrar uma sequência contínua de círculos que contêm as letras da palavra-chave.

Labirinto ("Maze") é uma estrutura composta de rotas complicadas. Neste tipo de quebra-cabeças deve encontrar um rota entre os dois pontos selecionados. O programa permite criar labirintos de forma livre, não só rectangulares ou quadrados.