|
Opções
|
Cross+A  Opções de quebra-cabeças Opções de quebra-cabeçasMuitos quebra-cabeças têm variações além das regras clássicas. O Cross+A pode resolver e criar essas variações de quebra-cabeças (na mesma janela que a versão clássica ou em uma janela separada como um novo tipo de quebra-cabeça).
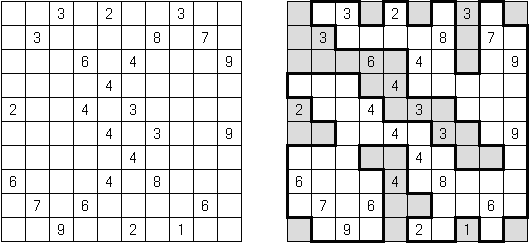
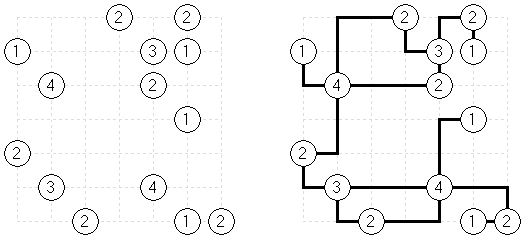
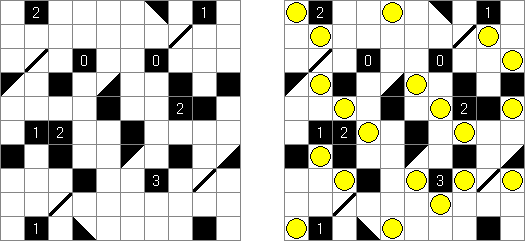
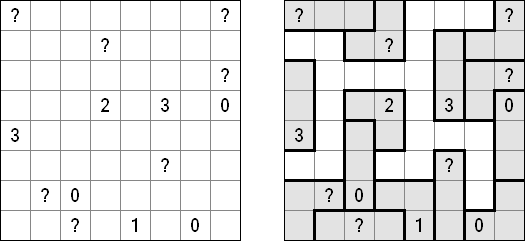
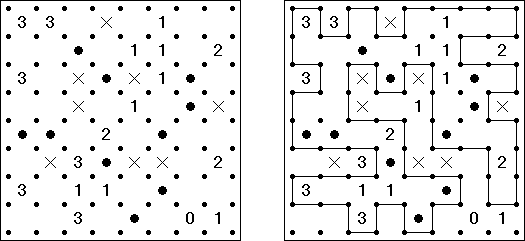
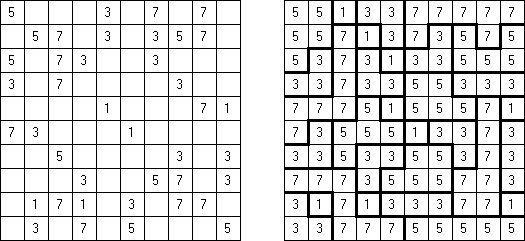
Slitherlink Ovelhas e lobos ("Sheep and Wolves") é uma variedade do quebra-cabeça Slitherlink: além dos dígitos de 0 a 3, também contém círculos pretos ("ovelhas") e cruzes pretas ("lobos"). No final da resolução do quebra-cabeça as "ovelhas" devem situar-se dentro de uma linha fechada ("no cercado") e os lobos fora da linha fechada ("fora do cercado").
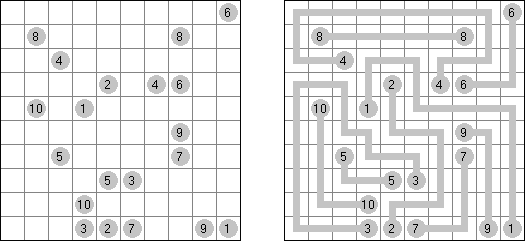
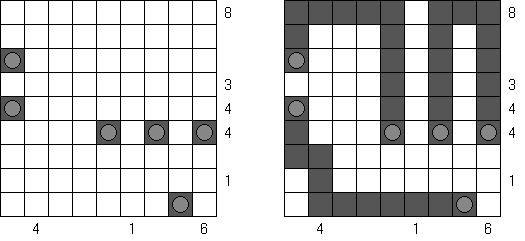
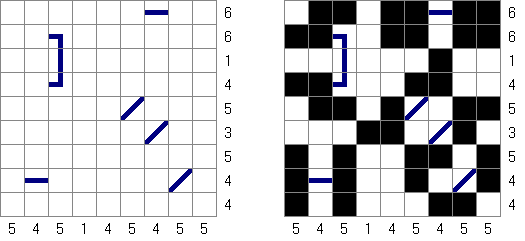
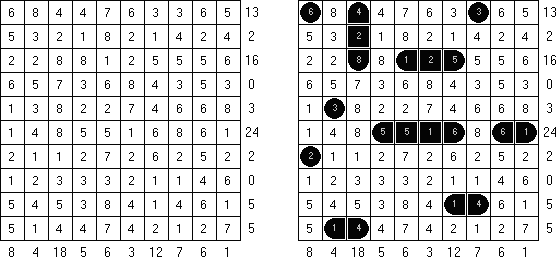
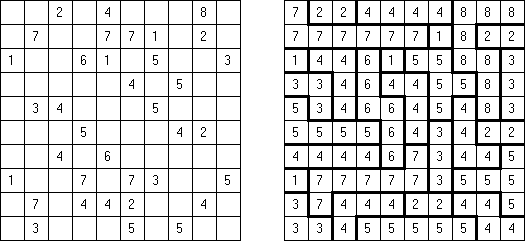
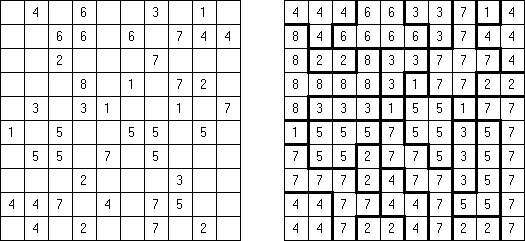
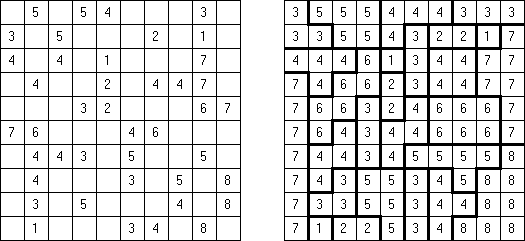
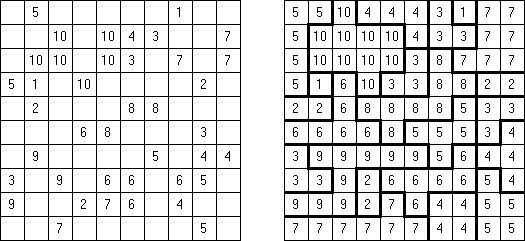
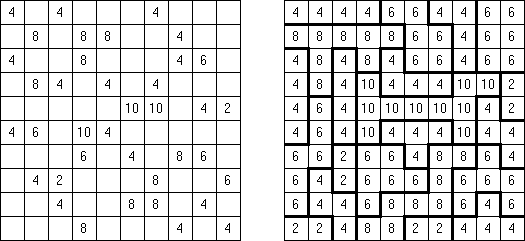
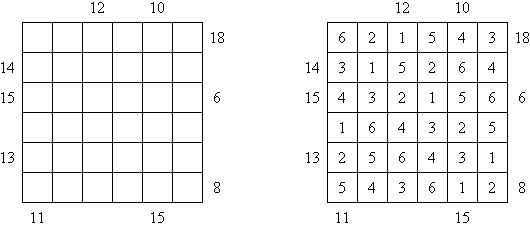
Batalha naval In Digital Battleships all cells of the grid contain numbers. The values on the right and bottom edges of the grid reveal the sum of the numbers in each of the ship pieces that appear in each respective row or column.
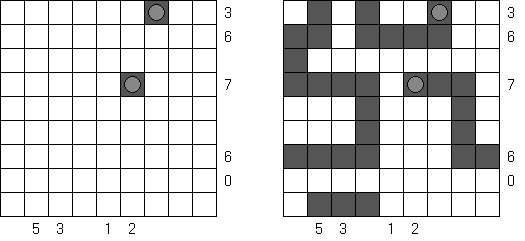
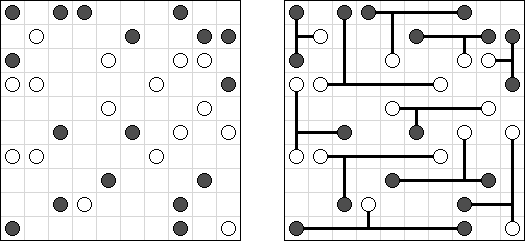
Retrograde Battleships ("Reverse Battleships") contains all segments of the ships in the grid. The aim is to find the correct locations of the ships. No ship may touch another, even diagonally.
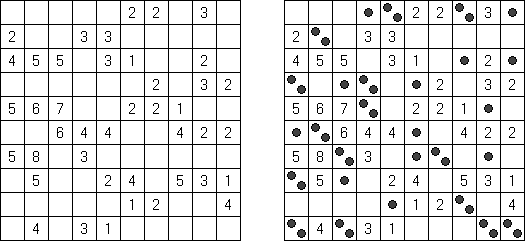
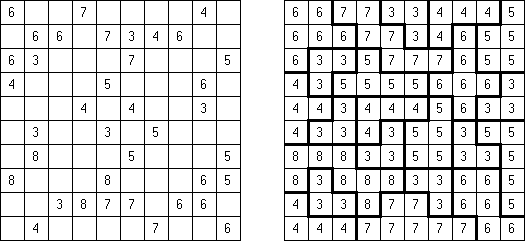
Fillomino No Rectangles Fillomino contém uma regra adicional: nenhum dos blocos deve ser dum formato rectangular ou quadrado.
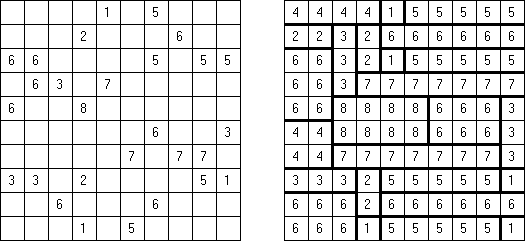
Only Rectangles Fillomino: todos os blocos devem ser retangulares ou quadrados.
No 2 x 2 Squares Fillomino: a grade não deve conter áreas do tamanho 2 x 2 que contenham os mesmos números.
Non-Consecutive Fillomino: as células de dois blocos que se tocam na horizontal ou vertical, não deve diferir por um.
Consecutive Fillomino: cada bloco deve tocar na horizontal ou na vertical com pelo menos um bloco, cujo tamanho difere por um.
No Row/Column Repeats Fillomino ("Deadomino"): todos os números iguais em uma linha ou coluna deve pertencer ao mesmo bloco. Por exemplo, se houver numa linha dois números "5", ambos pertencem ao mesmo bloco.
All Odds Fillomino: os tamanhos de todos os blocos são números ímpares.
All Evens Fillomino: os tamanhos de todos os blocos são números pares.
Nurikabe Line Nurikabe: a grid cannot contain five consecutive black cells in a row or column (2 x 2 cell area can be all black).
Pares Nurikabe difere da versão normal do quebra-cabeças Nurikabe no que cada "ilha" contém dois números cuja soma é igual à área da ilha.
Arranha-céus Sum Skyscrapers distingue-se do quebra-cabeças Arranha-céu ("Skyscrapers") pelo facto que os números fora do campo não significam o número dos edifícios visíveis, mas a soma de todos os andares destes edifícios.
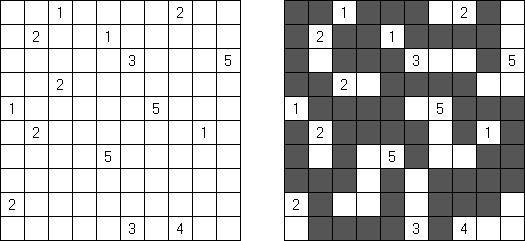
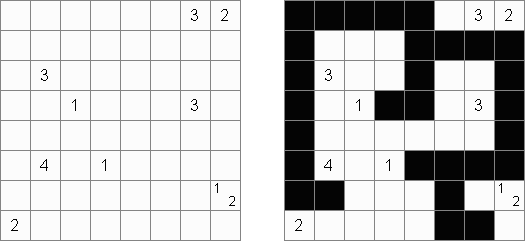
Tapa Existem muitas versões do quebra-cabeça Tapa. O programa Cross+A pode resolver algumas delas. No Tapa [Line] se aplica uma regra adicional: não deve haver uma linha de quatro quadrículas pretas consecutivas em uma linha horizontal ou vertical.
No Squares Tapa: não deve haver um quadrado 2 x 2 que consista apenas de quadrículas brancas.
Equal Tapa: o número das quadrículas brancas (excepto para as quadrículas que contêm números) deve ser igual ao número de quadrículas pretas.
B&W Tapa:
Tapa Islands:
Pata:
Tapa Balance: o número das quadrículas pretas na parte esquerda da retícula coincide com o número de células pretas na parte direita. As quadrículas brancas e as quadrículas com números não contam.
Tapa Row: a soma de todos os dígitos na linha é igual ao número de quadrículas pretas na mesma linha.
Tapa 1-n: todas as linhas e colunas devem conter quantidades diferentes de quadrículas pretas.
Dissected Tapa: as quadrículas pretas e as quadrículas brancas formam duas figuras congruentes. Duas figuras são chamadas congruentes se coincidem uma com a outra sendo superpostas.
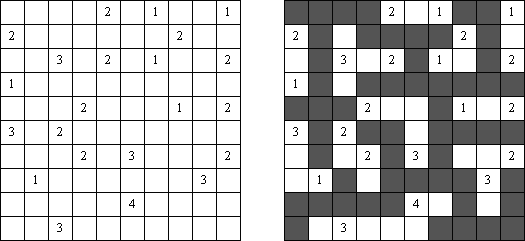
Tapa [Diagonal Neighbors]: cada célula preta deve ter pelo menos uma célula vizinha preta na diagonal.
Corral Inside/Outside Corral é uma variedade do quebra-cabeças Corral. Difere em que os números podem estar tanto dentro da linha fechada como fora. Em ambos os casos, o número indica o número de quadrículas "visíveis", incluindo a própria quadrícula com o número.
Arukone Arukone3:
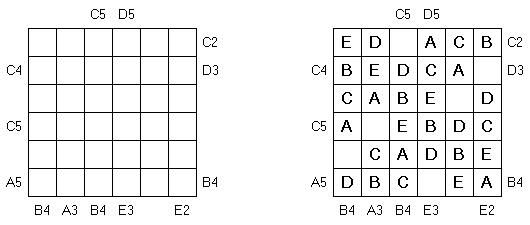
Simples como o ABC Not as Easy as ABC is a variation of Easy as ABC puzzle. The goal is to fill in the first letters of the alphabet on every row and every column exactly once. One cell in every row and every column remains empty. Letters and numbers on the outside indicate at what position you come across this letter when looking from that side (e.g. C2 means the C is the second letter encountered when looking from that side).
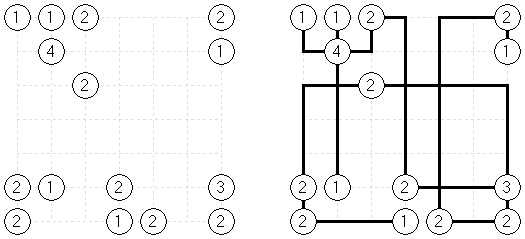
Ichimaga Crossing Ichimaga: the lines may cross other lines; the lines cannot change direction at the point of intersection.
Magnetic Ichimaga ("Jishaku-Ichimaga"): the circles with the same digits cannot be connected.
Snake Multiple Snakes: a grid contains multiple snakes. Head and tail of all snakes are given. Different snakes do not touch each other, even diagonally.
Toroidal Snake: a grid wraps around itself. A snake can go from one edge to another.
Campo minado Double Minesweeper: place mines into each empty cell in the grid, at most two mines per cell.
Mirukuti Milk Tease is a variation of Mirukuti ("Milk-T") puzzle. T-shaped line may connect:
Two circles of the same color must be connected by the straight-line segment of the T-shaped line.
Akari Mirror Akari ("!irakAkari!"): a square or rectangular grid contains diagonal walls (black triangles) with mirrors.
Tren Tren+:
Ghost Tren:
Mubunanba Mubunanba+:
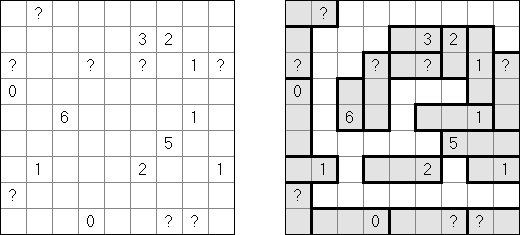
Yajilin Regional Yajilin (also known as "Yajilin (Regions)") is a square or rectangular grid divided into regions. The aim is to blacken some cells and to draw a single non-intersecting loop through all the white cells. A number in a region indicates the number of black cells in that region. A region without a number can contain any amount of black cells. No two black cells can share a border. The loop may visit numbered cells; numbered cells can be blackened.
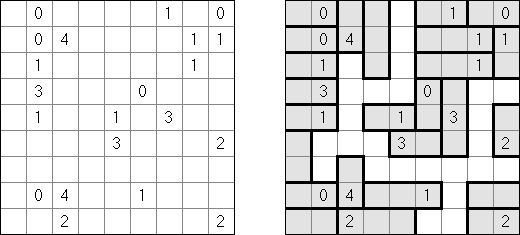
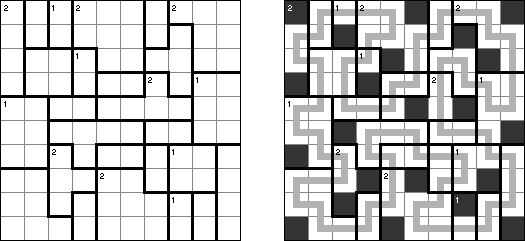
LITS Double LITS has one difference from the classic variant of the puzzle: each region must contain two tetrominoes. These two tetrominoes within a region cannot touch each other horizontally or vertically (only diagonally); they can be the same or different shapes.
Kapama Sunglasses is a logic puzzle. A rectangular or square grid contains lines ("bridges") in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes ("lenses") are symmetrical with respect to a bridge. Two lenses may not share an edge. Cells with bridges can not be blacken. Numbers outside the grid show the number of black cells in a corresponding row or column.
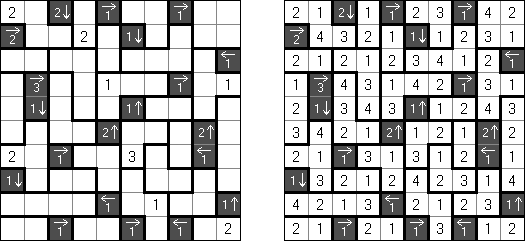
Makaro Masakuchi is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. The grid may contain black cells with arrows and numbers: the arrow points at the greatest number among the four cells around (up, under, left, right) the black cell. The number in the black cell shows the difference between the greatest number and the second highest number in all orthogonally adjacent cells around the black cell.
|

![Tapa [Line]](../data/tapa1.gif)








![Tapa [Diagonal Neighbors]](../data/tapa11.gif)