|
Cross+A  谜题种类 谜题种类某些拼图除了经典规则外,还存在变体形式。Cross+A 应用程序能够解决并创建这些拼图变体(既可在与经典版本相同的窗口中进行,也可在独立窗口中作为全新类型的拼图进行)。
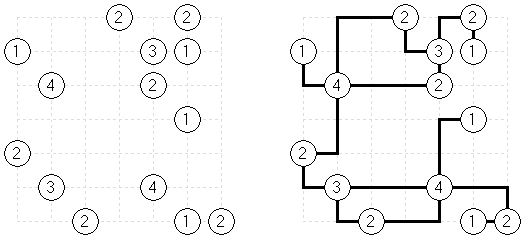
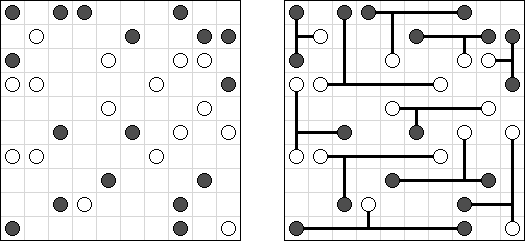
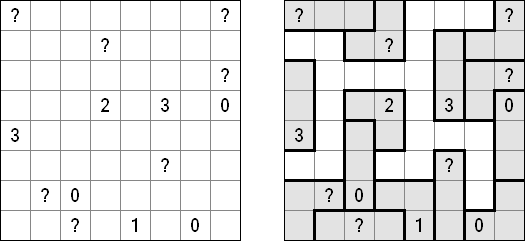
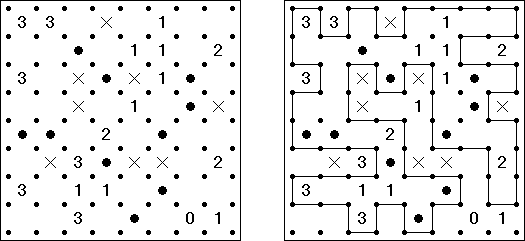
数回(Slitherlink) Sheep and Wolves("狼和羊"):除了0至3 数字以外,在格网中有黑圆圈("羊")和黑交叉符号("狼")。需要划一条不间断的线,所有的"羊"都要处在该条线内,而"狼"要处在该条线外。
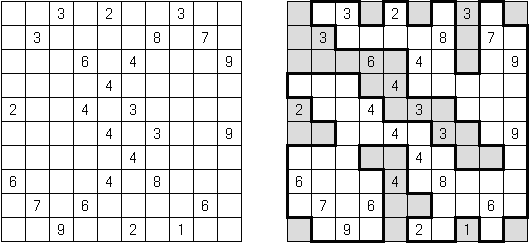
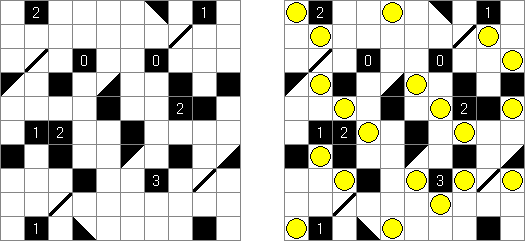
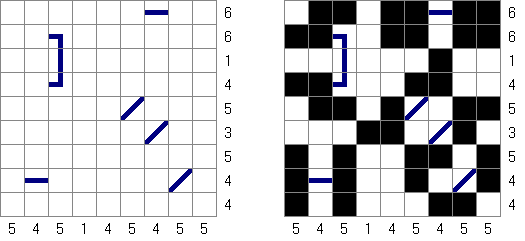
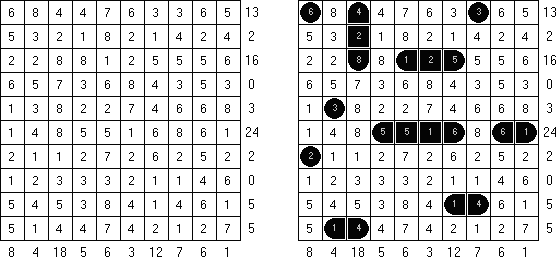
战舰(Battleships) Digital Battleships – 在网格中的所有方格包含数目。需要在盘面上摆放"船舰",主要条件是“隐藏”的数字中船舰在对角和邻边都不可以相邻。
Retrograde Battleships ("Reverse Battleships") contains all segments of the ships in the grid. The aim is to find the correct locations of the ships. No ship may touch another, even diagonally.
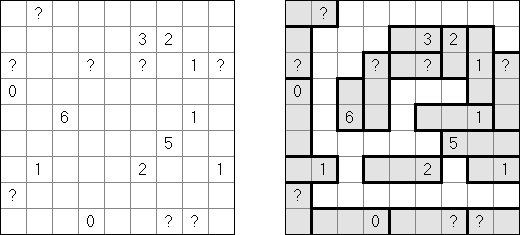
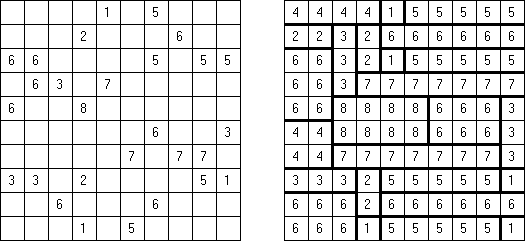
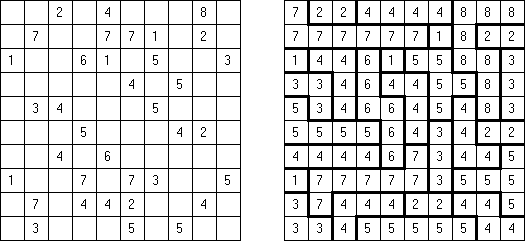
码牌(Fillomino) No Rectangles Fillomino有附加条件:不得构成长方形或正方形的大块。
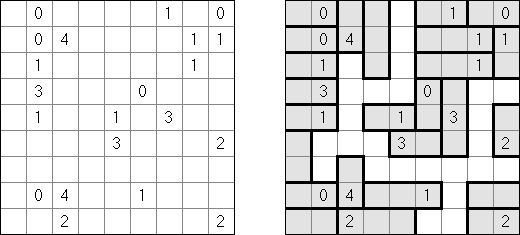
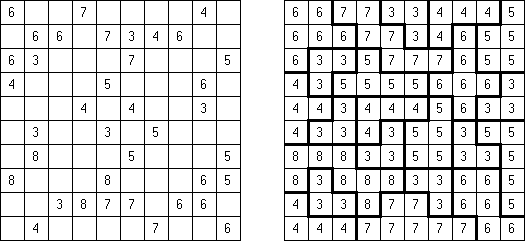
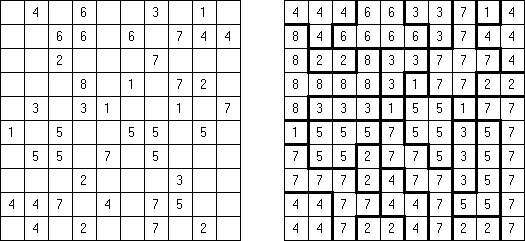
Only Rectangles Fillomino:所有的大块都是长方形或正方形。
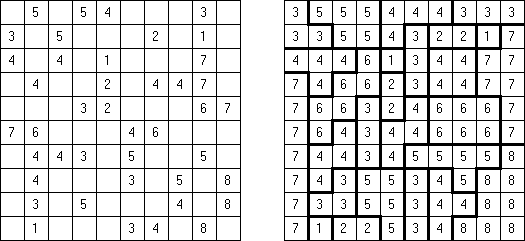
No 2 x 2 Squares Fillomino:在格网中不得构成包含相同数字的 2x2大块。
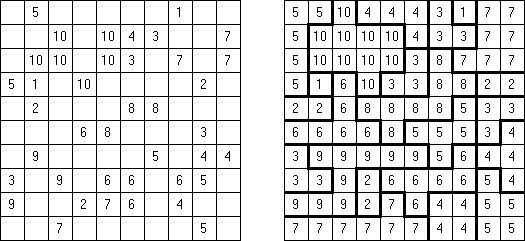
Non-Consecutive Fillomino:任何大块的数字和在横向或纵向邻接的大块的数字要至少大于或小于二。
Consecutive Fillomino:任何大块的数字和在横向或纵向邻接的大块的数字要大于或小于一。
No Row/Column Repeats Fillomino ("Deadomino"):在任何行或列里的相同的数字都属于一个大块。例如,在一条列里有两个"5"数字,则它们都属于一个大块。
All Odds Fillomino:任何大块数字大小相当于奇数。
All Evens Fillomino:任何大块大小相当于偶数。
数墙(Nurikabe) Line Nurikabe: a grid cannot contain five consecutive black cells in a row or column (2 x 2 cell area can be all black).
Pairs Nurikabe ("双数墙")与普通的Nurikabe("数墙")主要差别是每个"岛"含有两个数字,数字之和等于该岛的面积。
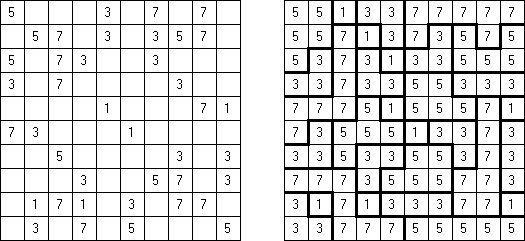
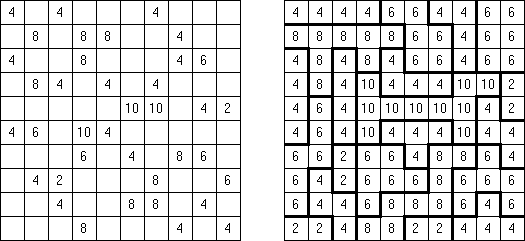
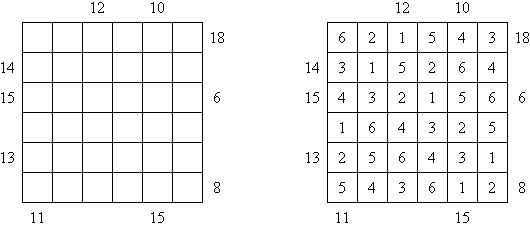
摩天楼(Skyscrapers) Sum Skyscrapers 与Skyscrapers谜题的不同点是格网外面的数字不表明可看到的楼房数量,而是表明那些楼房的所有楼层之和。
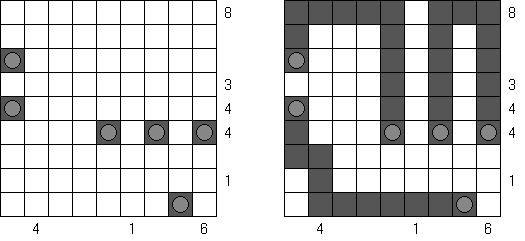
塔帕(Tapa) Tapa这种谜题有各种各样的玩法。Cross+A软件能解答其中几种。 Tapa [Line]有附加规则:不得有水平或垂直一连四个黑格的线。
No Squares Tapa:不得有只含白格的2×2正方体。
Equal Tapa: 除了含数字的方格以外,白色方格的数量应等于黑色方格的数量。
B&W Tapa:
Tapa Islands:
Pata:
Tapa Balance: 格网左边的黑色方格数量应等于格网右边的黑色方格数量,白色方格和有数字的方格不影响到在格网两个部分中黑色方格的平衡。
Tapa Row: 一行所有的数字之和等于该行黑色方格的数量。
Tapa 1-n:每个行和列所有的黑色方格数量不得相同。
Dissected Tapa:黑色方格和白色方格应形成两个全等的图形。能够完全重合的两个图形叫做全等的图形。
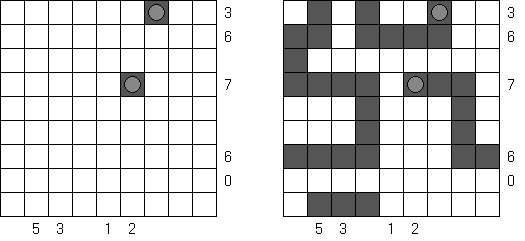
Tapa [Diagonal Neighbors]: every black cell must have at least one diagonally adjacent black cell.
畜栏(Corral) Inside/Outside Corral是Corral谜题的一种。其主要的差别是数字不仅放在闭合的线内,也放在闭合的线外。在两种游戏中数字表明水平和垂直看到的方格数量,包括该数字的方格。
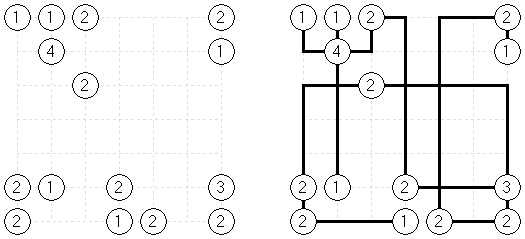
数连(Arukone) Arukone3:
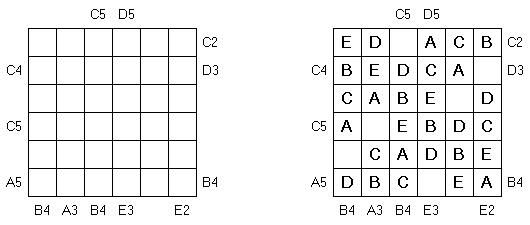
易如ABC (Easy as ABC) Not as Easy as ABC is a variation of Easy as ABC puzzle. The goal is to fill in the first letters of the alphabet on every row and every column exactly once. One cell in every row and every column remains empty. Letters and numbers on the outside indicate at what position you come across this letter when looking from that side (e.g. C2 means the C is the second letter encountered when looking from that side).
位置(Ichimaga) Crossing Ichimaga: the lines may cross other lines; the lines cannot change direction at the point of intersection.
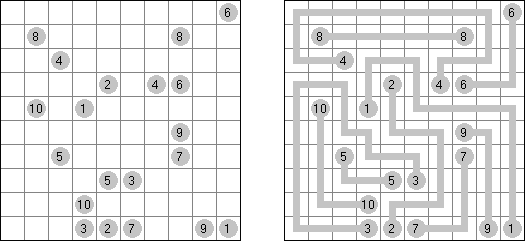
Magnetic Ichimaga ("Jishaku-Ichimaga"): the circles with the same digits cannot be connected.
长蛇(Snake) Multiple Snakes: a grid contains multiple snakes. Head and tail of all snakes are given. Different snakes do not touch each other, even diagonally.
Toroidal Snake: a grid wraps around itself. A snake can go from one edge to another.
扫雷(Minesweeper) Double Minesweeper: place mines into each empty cell in the grid, at most two mines per cell.
奶茶(Mirukuti) Milk Tease is a variation of Mirukuti ("Milk-T") puzzle. T-shaped line may connect:
Two circles of the same color must be connected by the straight-line segment of the T-shaped line.
点灯(Light Up) Mirror Akari ("!irakAkari!"): a square or rectangular grid contains diagonal walls (black triangles) with mirrors.
停车场(Tren) Tren+:
Ghost Tren:
移动数(Mubunanba) Mubunanba+:
数矢(Yajilin) Regional Yajilin (also known as "Yajilin (Regions)") is a square or rectangular grid divided into regions. The aim is to blacken some cells and to draw a single non-intersecting loop through all the white cells. A number in a region indicates the number of black cells in that region. A region without a number can contain any amount of black cells. No two black cells can share a border. The loop may visit numbered cells; numbered cells can be blackened.
LITS骨牌(LITS) Double LITS has one difference from the classic variant of the puzzle: each region must contain two tetrominoes. These two tetrominoes within a region cannot touch each other horizontally or vertically (only diagonally); they can be the same or different shapes.
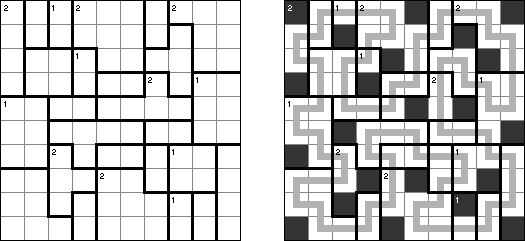
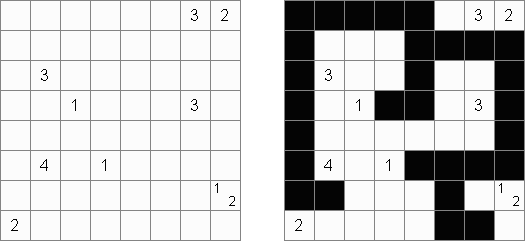
闭合(Kapama) Sunglasses is a logic puzzle. A rectangular or square grid contains lines ("bridges") in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes ("lenses") are symmetrical with respect to a bridge. Two lenses may not share an edge. Cells with bridges can not be blacken. Numbers outside the grid show the number of black cells in a corresponding row or column.
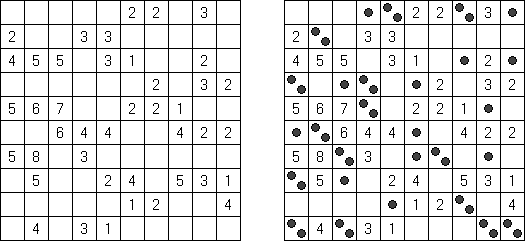
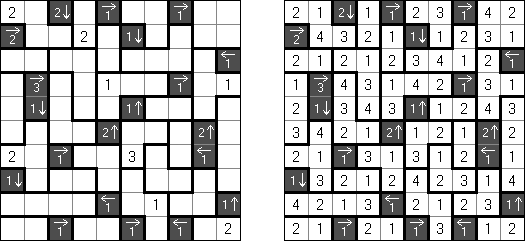
马卡罗(Makaro) Masakuchi is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. The grid may contain black cells with arrows and numbers: the arrow points at the greatest number among the four cells around (up, under, left, right) the black cell. The number in the black cell shows the difference between the greatest number and the second highest number in all orthogonally adjacent cells around the black cell.
|

![Tapa [Line]](../data/tapa1.gif)








![Tapa [Diagonal Neighbors]](../data/tapa11.gif)