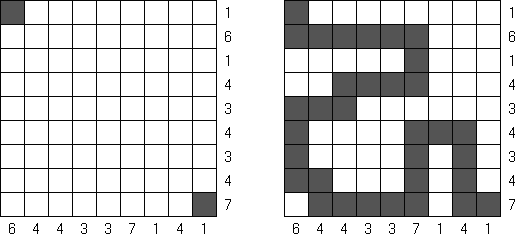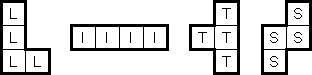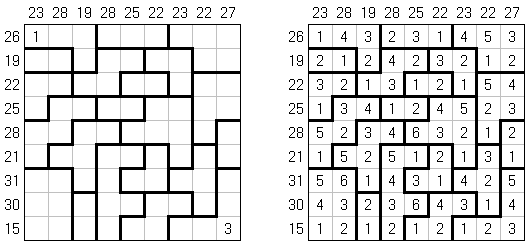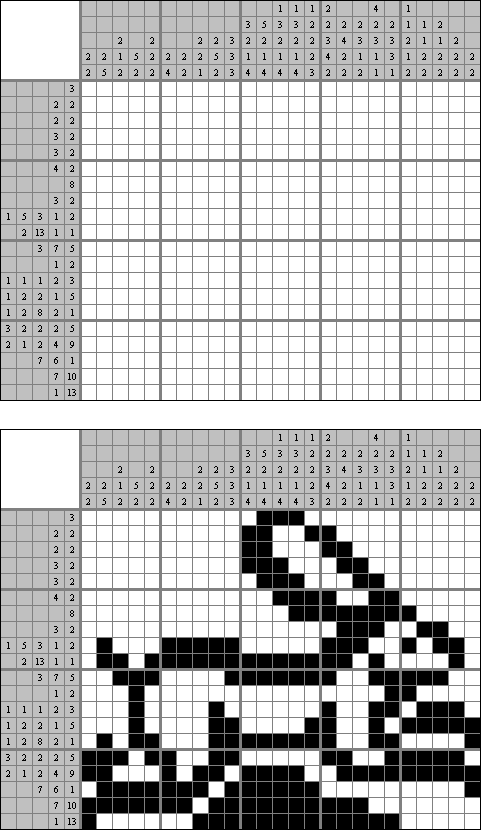
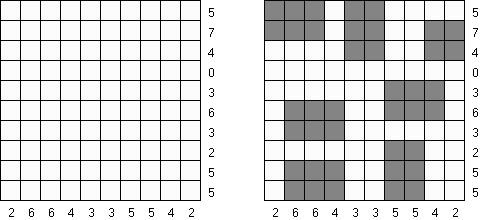
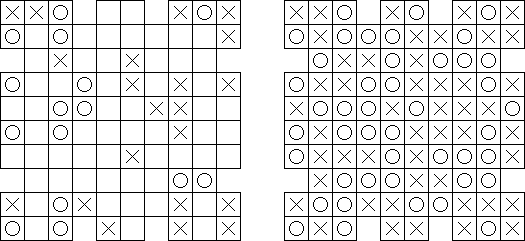
Cross+A Puzzles

Cross+A kann viele Arten von Logikrätseln lösen und erzeugen. Das erstellte Rätsel kann als Grafikdatei gespeichert werden (Windows Bitmap, Windows Metafile, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF und CorelDRAW Formate werden unterstützt). Auch die Serien-Erstellung von Puzzles ist möglich.

Nonogramm (auch bekannt als "Griddler", "CrossPix", "Hanjie") ist eine Art von Puzzle, bei der ein Bild in Übereinstimmung mit den Zahlen am linken und oberen Rand gemalt werden soll. Das Bild besteht aus gefüllten und leeren Kästchen. Die Zahlen zeigen an, wie viele Gruppen von gefüllten oder kolorierten Kästchen in jeder Reihe oder Säule enthalten sind und wie viele ununterbrochene kolorierte Kästchen jede Gruppe enthält.

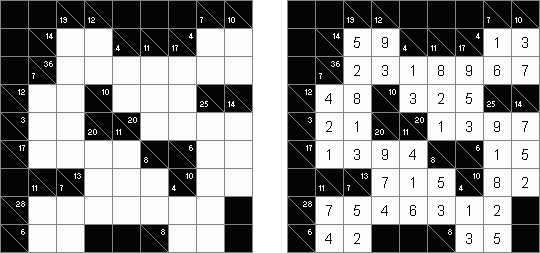
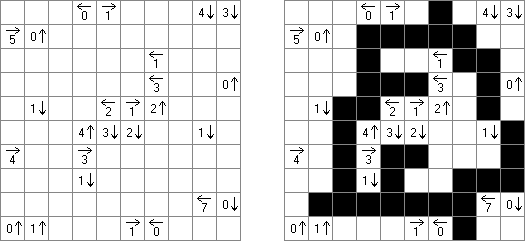
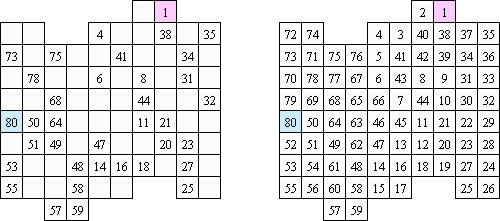
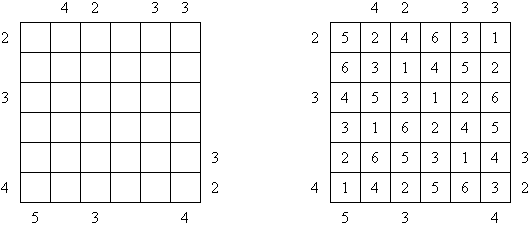
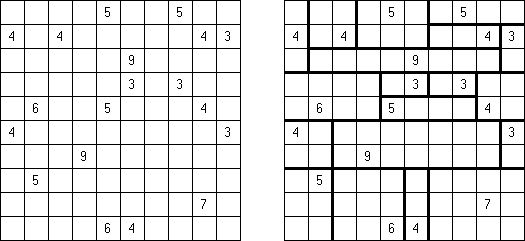
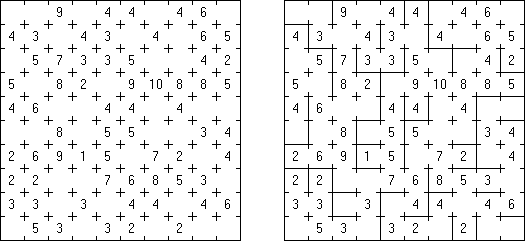
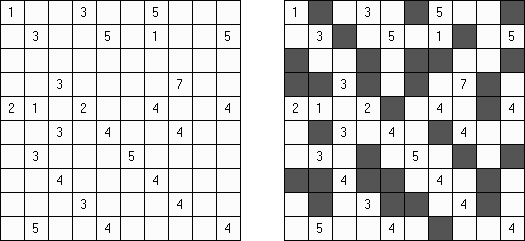
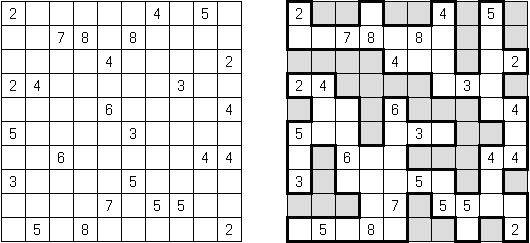
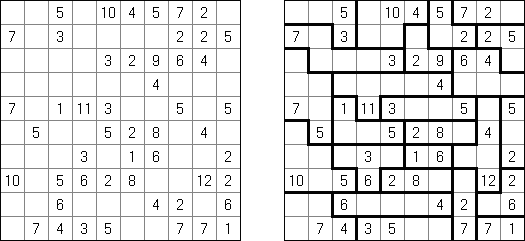
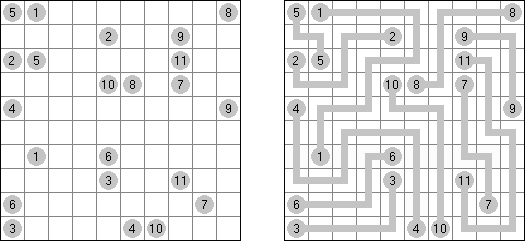
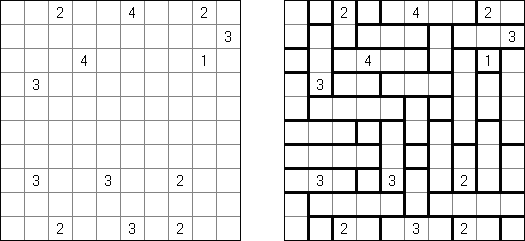
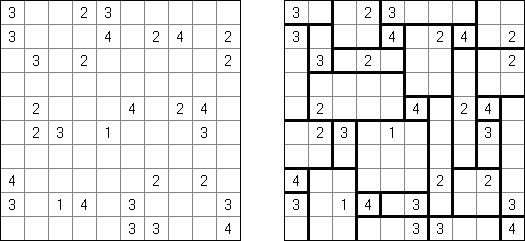
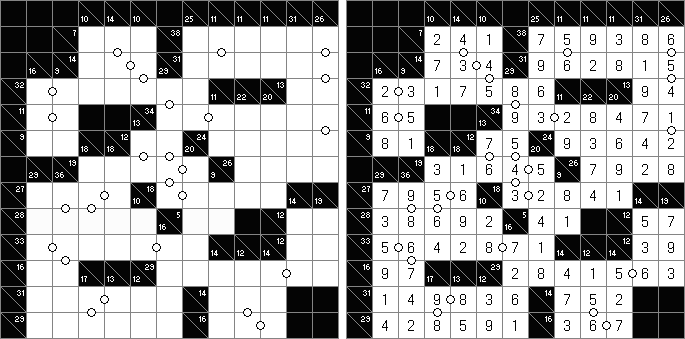
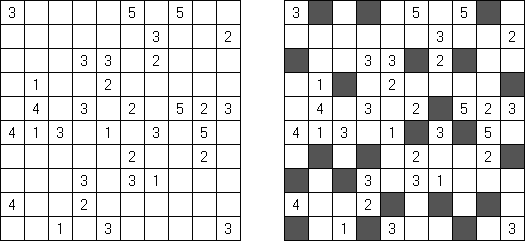
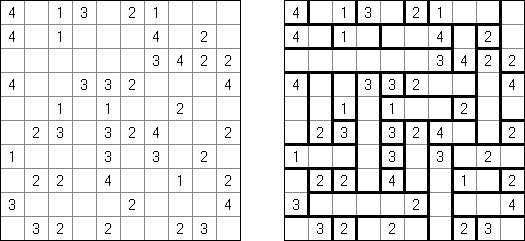
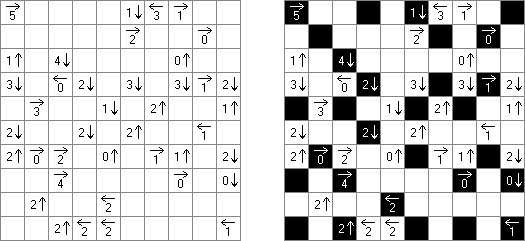
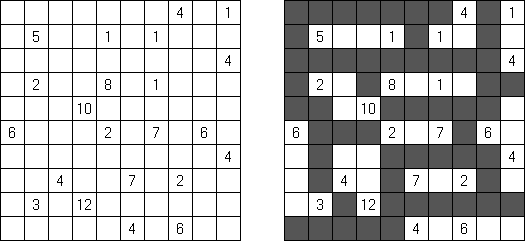
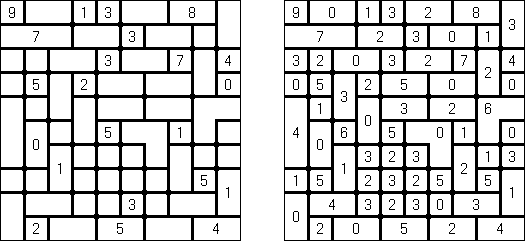
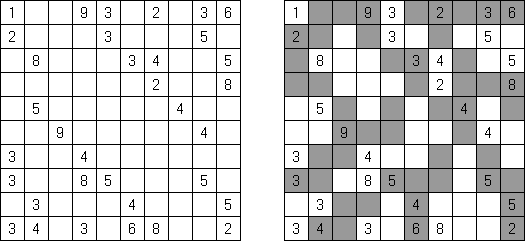
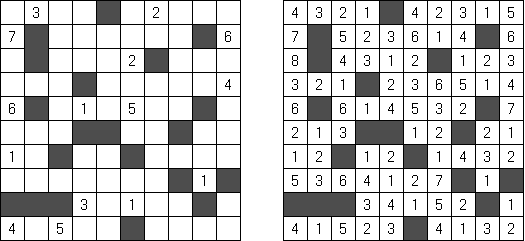
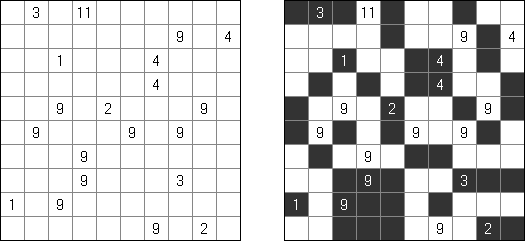
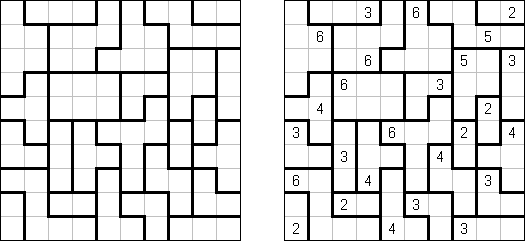
Kakuro (auch bekannt als "Cross Sums" = Kreuzsummenrätsel) ist ein logisches Puzzle - das mathematische Äquivalent zu Kreuzworträtseln.

Kakuro besteht aus einem Spielfeld mit gefüllten und leeren Feldern ähnlich wie bei einem Kreuzworträtsel. Einige schwarze Felder enthalten einen Schrägstrich von oben links nach unten rechts mit Zahlen darin, den "Summen". Eine Zahl in der oberen rechten Ecke gehört zu einer quer liegenden Summe und eine in der unteren linken Ecke zu einer vertikalen Summe.

Die Aufgabe von Kakuro besteht darin, Ziffern von 1 bis 9 so einzufügen, dass ihre Summe der zugehörigen Zahl entspricht. Dabei darf aber keine Zahl doppelt vorkommen. Für die Gesamtsumme 6 können Sie zum Beispiel 1 und 5, 2 und 4, aber nicht 3 und 3 verwenden.

Das Spielfeld von einem Kakuro-Puzzle kann jede Größe haben; jedoch sind die enthaltenen Quadrate üblicherweise symmetrisch angeordnet.

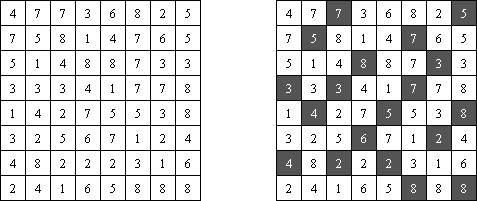
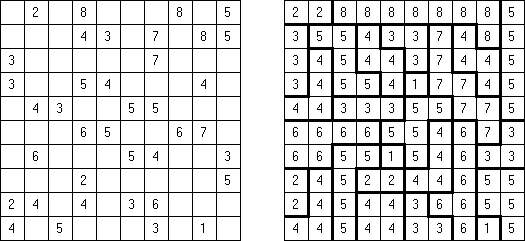
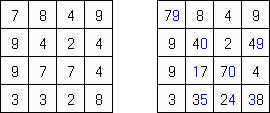
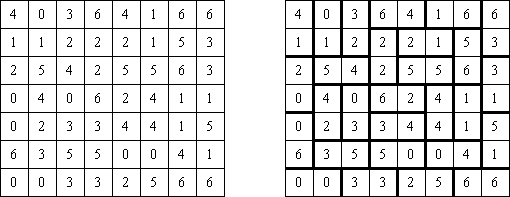
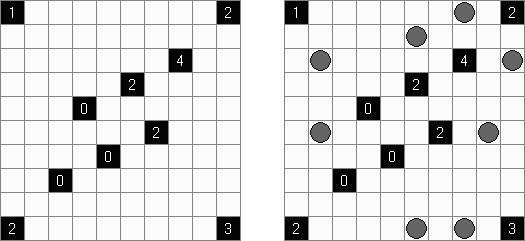
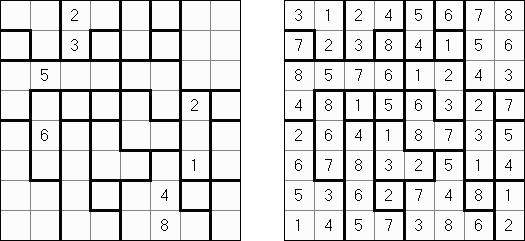
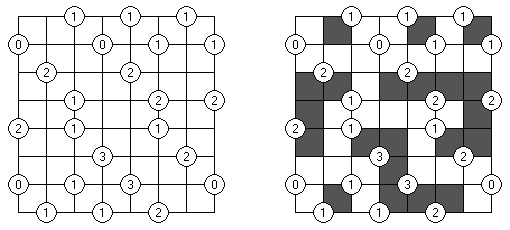
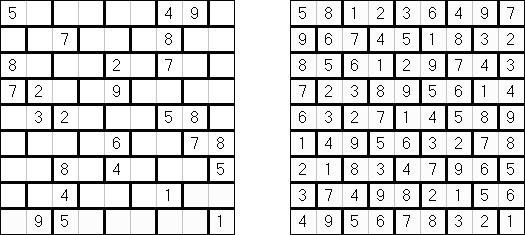
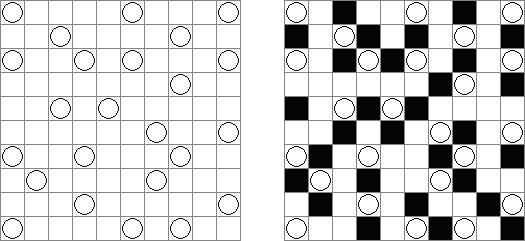
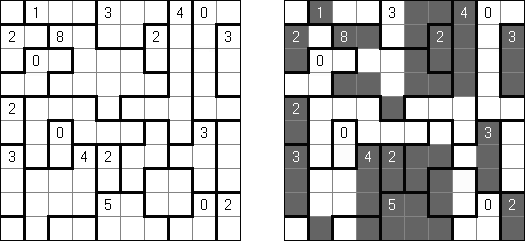
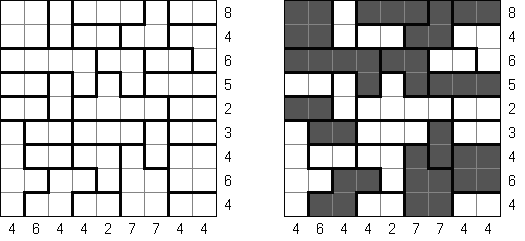
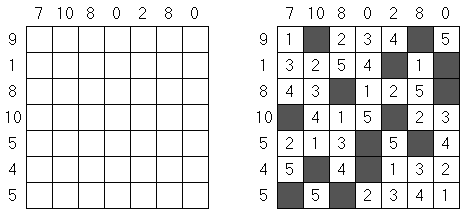
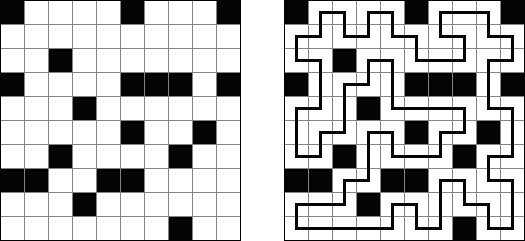
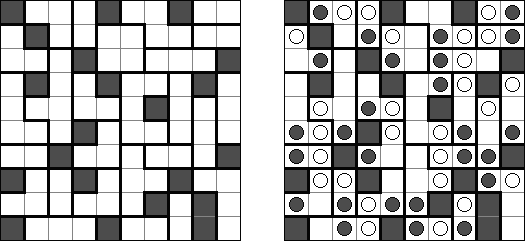
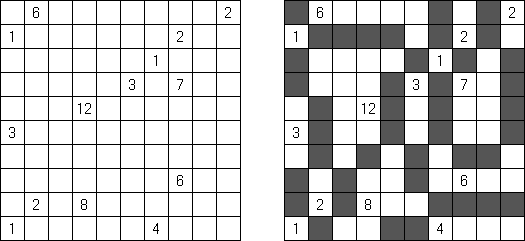
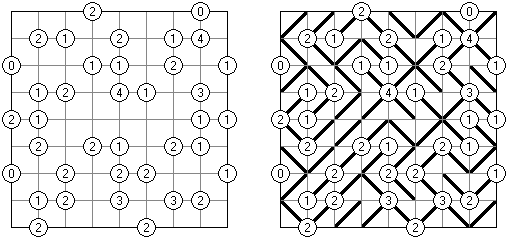
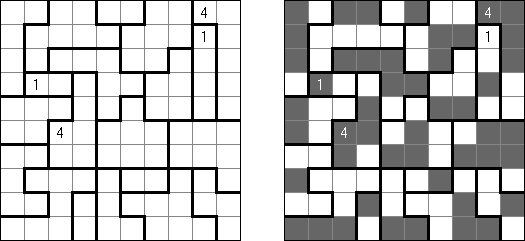
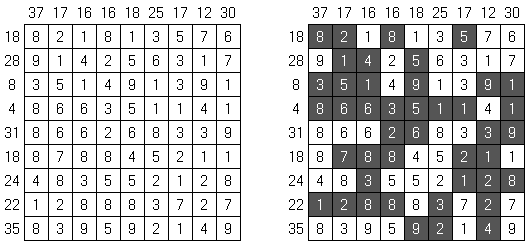
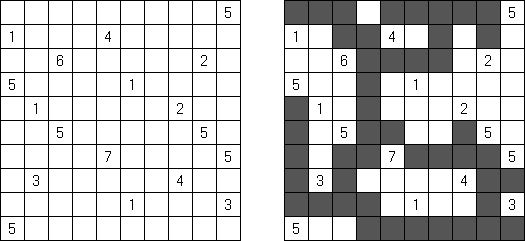
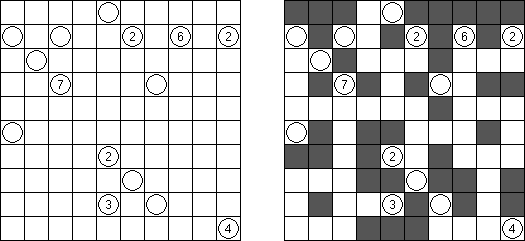
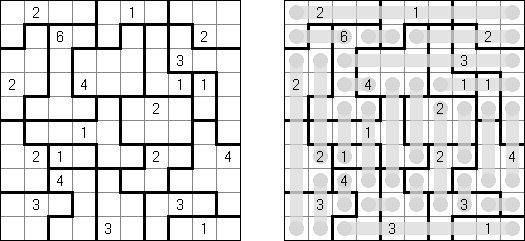
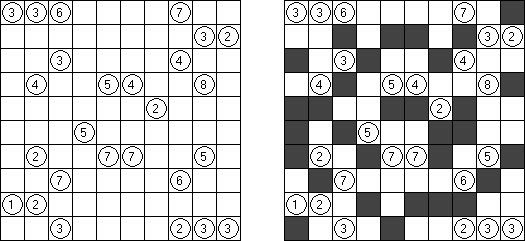
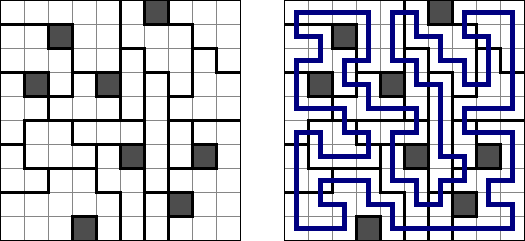
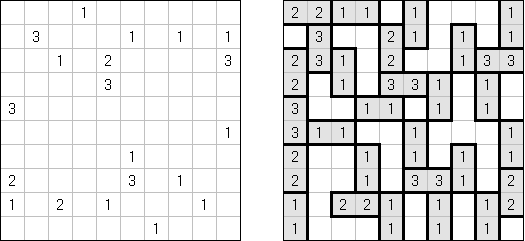
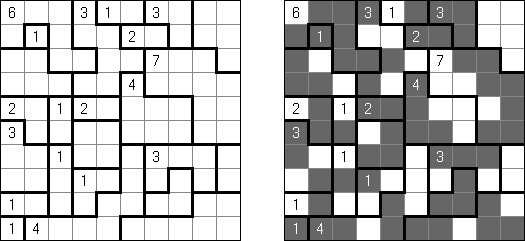
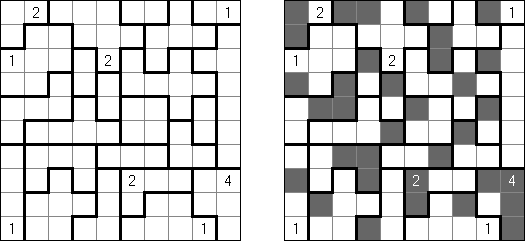
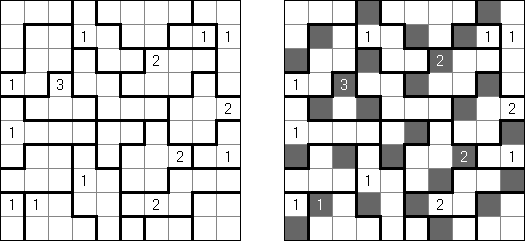
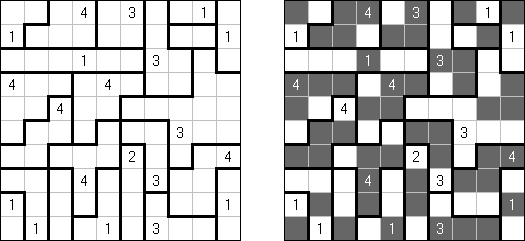
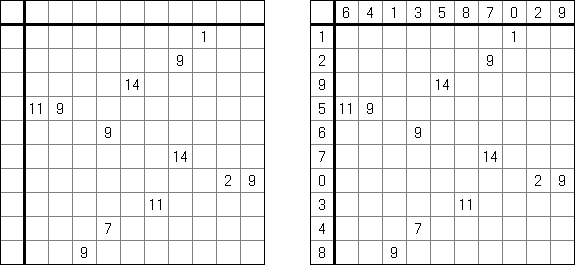
Hitori (jap. "Hitori ni shite kure"; wörtlich: "Lass mich allein!") wird auf einem quadratischen Gitter gespielt. Am Anfang enthält jedes Feld eine Zahl. Ziel ist es, einige Felder schwarz zu übermalen, sodass in keiner Reihe oder Spalte doppelte Zahlen vorkommen - vergleichbar der Lösung eines Soduko Puzzles (bis auf die schwarzen Felder im Gitter).

Außerdem sind orthogonale Verbindungen wichtig; geschwärzte Felder dürfen nicht orthogonal verbunden sein, während die anderen Felder über orthogonale Verbindungen eine einzige zusammenhängende Gruppe bilden müssen (d.h. zwei schwarze Felder dürfen nicht an den Kanten zusammenhängen und alle weißen Felder müssen horizontal oder vertikal verbunden sein, sodass sie eine zusammenhängende Form bilden).

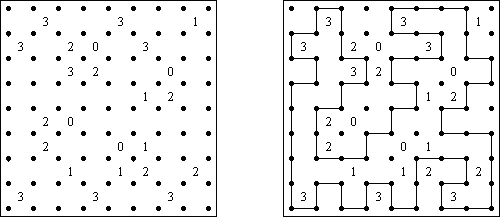
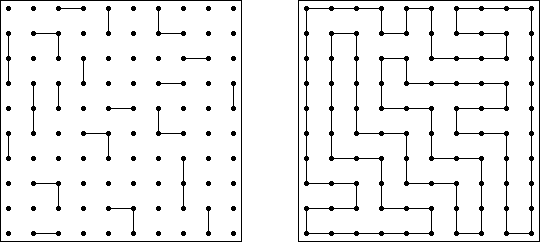
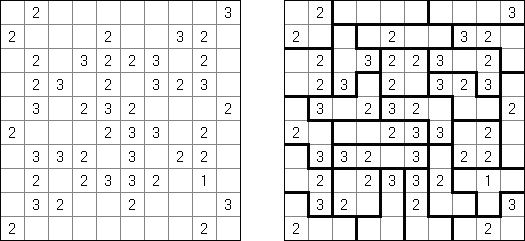
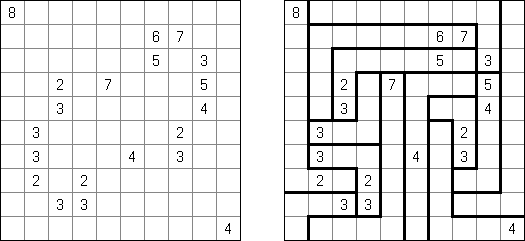
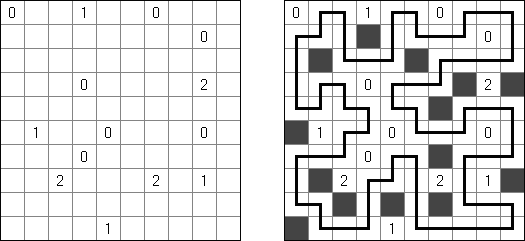
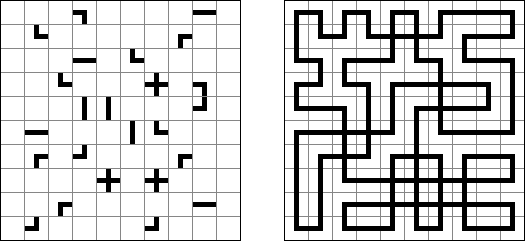
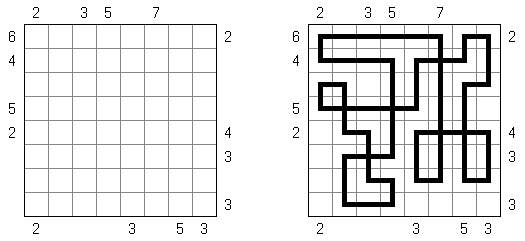
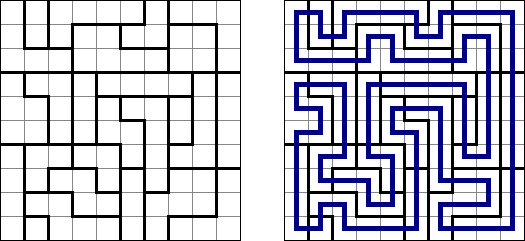
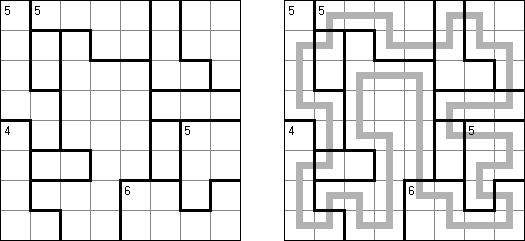
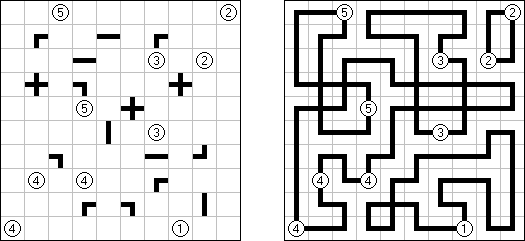
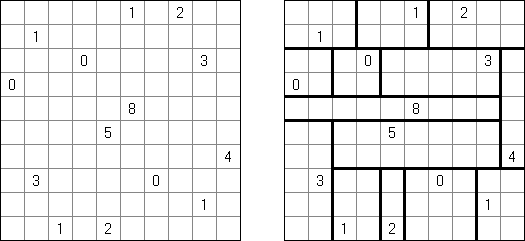
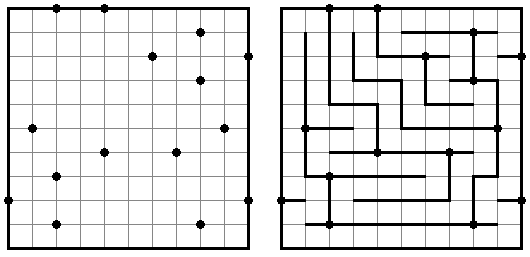
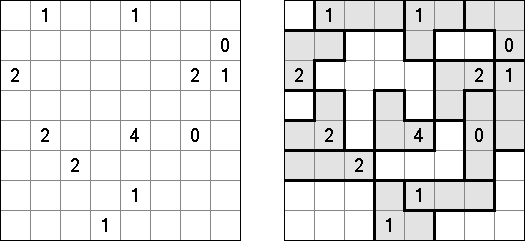
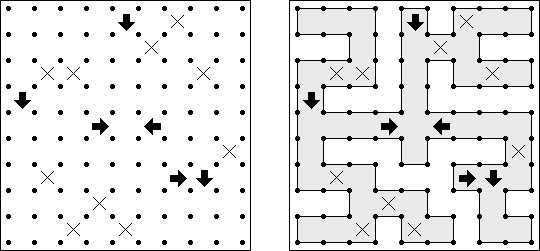
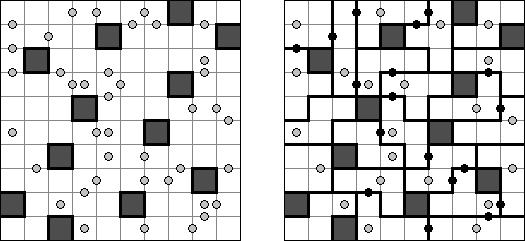
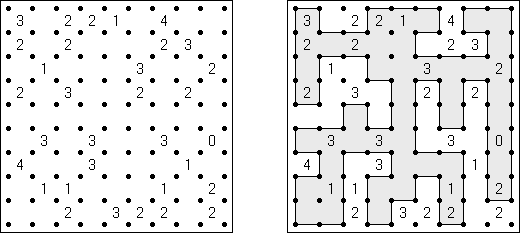
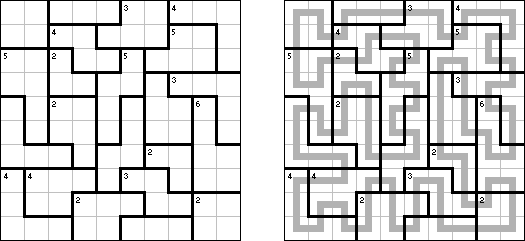
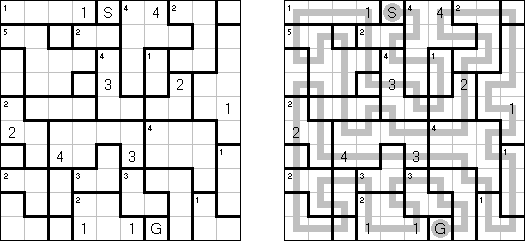
Schlangenlinie (auch bekannt als "Slitherlink", "Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin", "Great Wall of China", "Number Line", "Heiliger Pfad", "Rundweg", "Gartenzaun", "Suriza") ist ein logisches Puzzle. Es wurde von Nikoli Puzzles in Japan erfunden.

Schlangenlinie wird auf einem rechteckigen Gitter aus Punkten gespielt. Einige der Quadrate, die durch die Punkte gebildet werden, enthalten Zahlen. Ziel ist es, horizontal und vertikal benachbarte Punkte so zu verbinden, dass die Linien einen einzigen in sich geschlossenen Linienzug bilden.

Dabei geben die Zahlen in den Quadraten an, wie viele der vier Seiten Teile des Linienzuges sind.

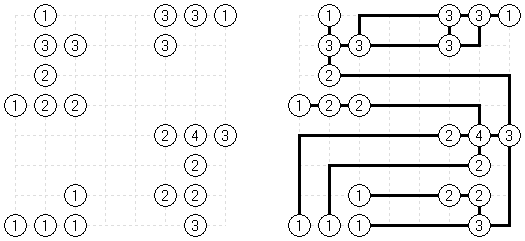
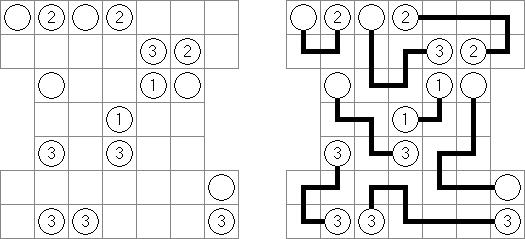
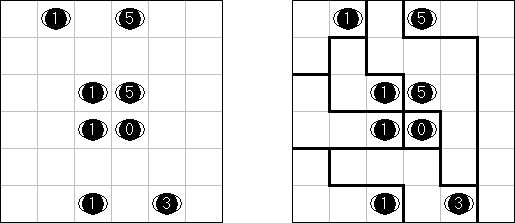
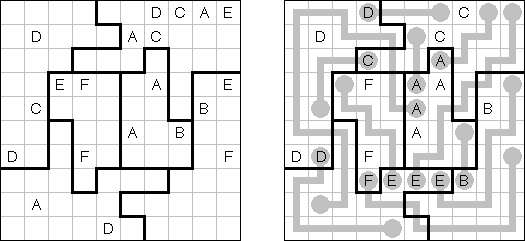
Link-a-Pix (auch bekannt als "Ketten" oder "Paint by Pairs") besteht aus einem Rastergitter, bei dem einige Felder mit Nummern versehen sind; Zahlenpaare müssen korrekt zugeordnet und in einer zusammenhängenden Kette verbunden werden, sodass die Anzahl der verbundenen Felder dieser Zahl entspricht. Felder, die '1' enthalten, repräsentieren eine Verkettung, die die Länge genau eines Feldes hat. Die Verkettung kann in jede horizontale oder vertikale Richtung gehen. Verkettungen dürfen andere Verkettungen nicht kreuzen.

In einem sauber konstruierten Puzzle gibt es nur eine einzige Möglichkeit, alle Felder zu verbinden. Am Ende werden die Felder, die Verkettungslinien darstellen, ausgemalt; der Kontrast zu den leeren Feldern bringt ein verborgenes Bild zum Vorschein.

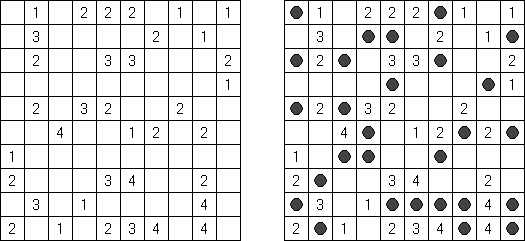
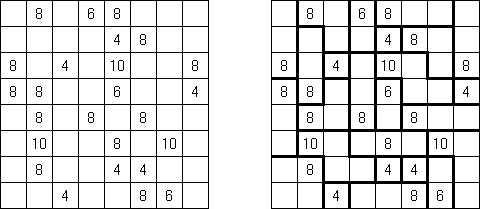
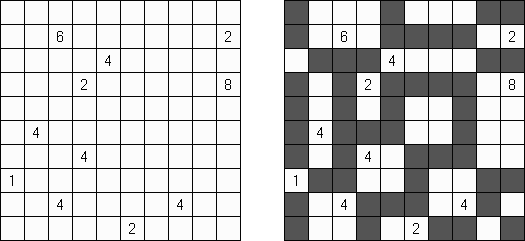
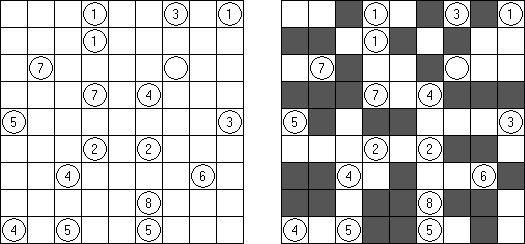
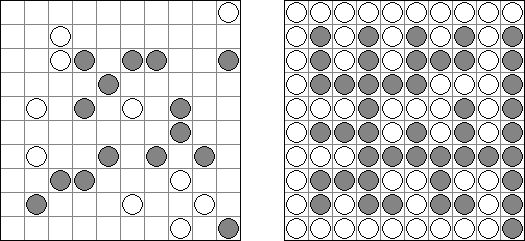
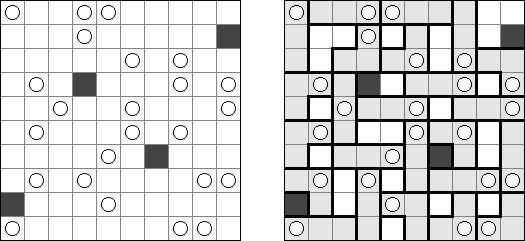
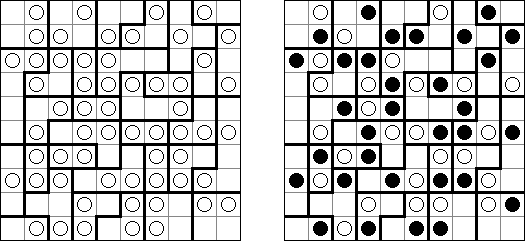
Fill-a-Pix (auch bekannt als "Mosaik", "Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") besteht aus einem Gitter mit verstreuten Schlüsselzahlen. Jede Zahl gibt an, wie viele der neun Felder - das Feld mit der Zahl als Mittelpunkt und die acht umgebenden - ausgefüllt werden sollen.

Man muss herausfinden, welche Felder ausgefüllt werden und welche leer bleiben müssen, bis das versteckte Bild vollständig sichtbar ist.

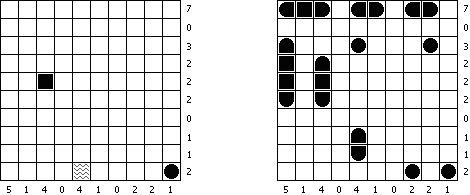
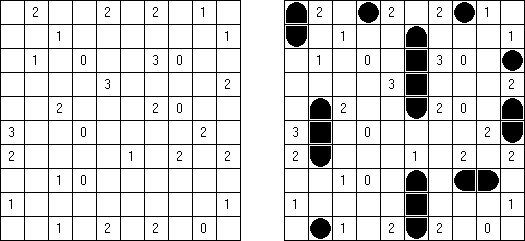
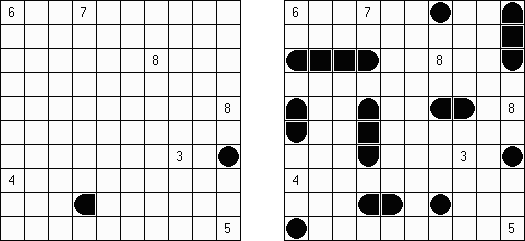
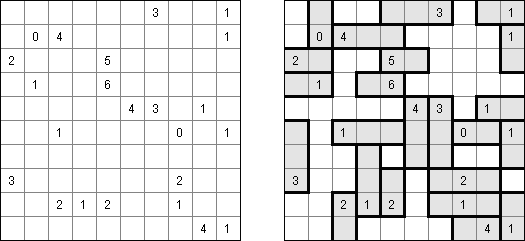
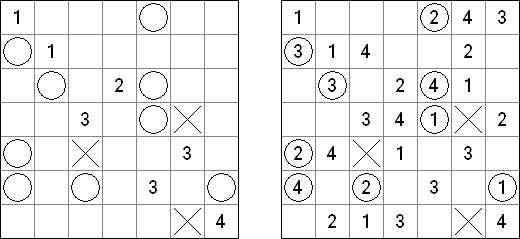
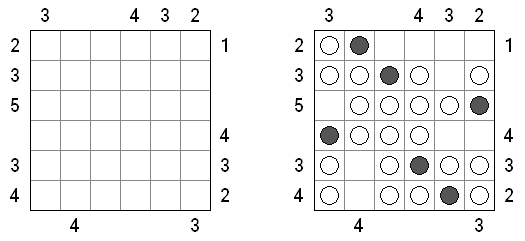
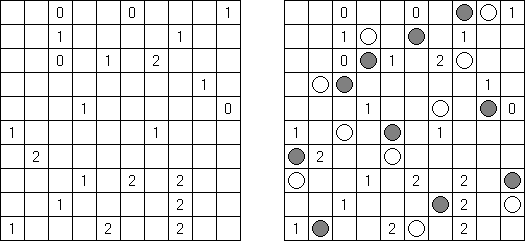
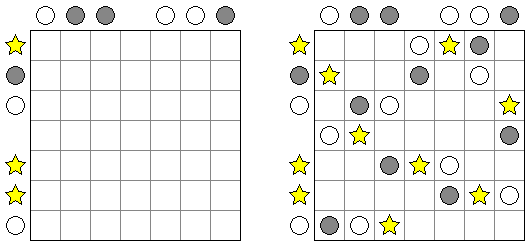
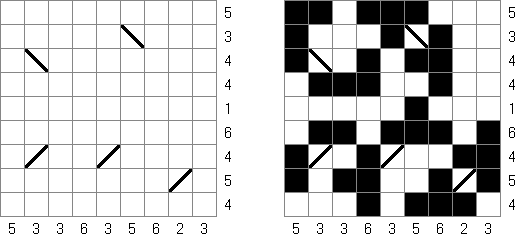
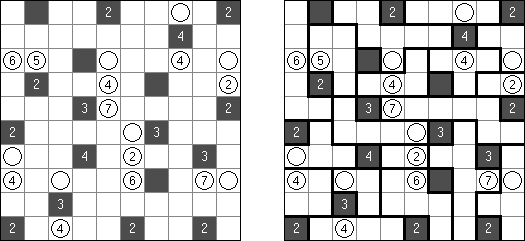
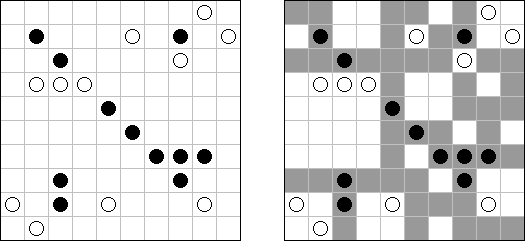
Marinespiel (auch bekannt als "Bimaru", "Flottenmanöver", "Seeschlacht", "Battleships", "Solitaire Battleships", "Battleship Solitaire") ist ein logisches Puzzle, welches auf dem bekannten Ratespiel "Schiffe versenken" basiert. In einem quadratischen Rastergitter mit 10 x 10 Feldern ist eine Flotte von Kampfschiffen verteilt. Es gibt ein Schlachtschiff mit 4 Feldern, zwei Kreuzer mit 3 Feldern, drei Zerstörer mit 2 Feldern und vier Unterseeboote mit 1 Feld. Jedes Schiff belegt eine Anzahl von fortlaufenden horizontalen oder vertikalen Feldern im Rastergitter. Die Schiffe sind so platziert, dass kein Boot ein anderes an den Seiten beruhrt, auch nicht diagonal. An den Ecken durfen sie sich beruhren.

Die Zahlen unterhalb und auf der rechten Seite des Rastergitters geben an, wie viele Felder in den zugehörigen Reihen oder Spalten von Schiffen besetzt werden. Gelegentlich können manche Felder ein Schiff- oder Wassersegment als Start-Tipp für das Puzzle enthalten. Die Aufgabe besteht darin herauszufinden, wo sich alle Schiffe befinden.

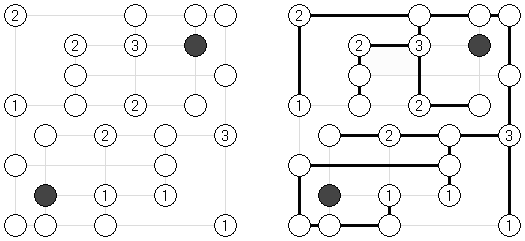
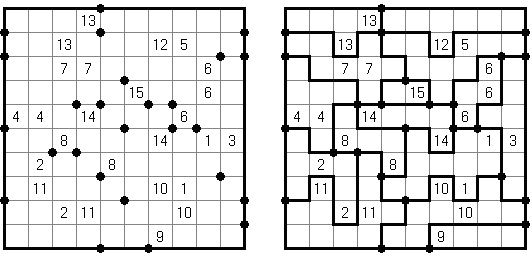
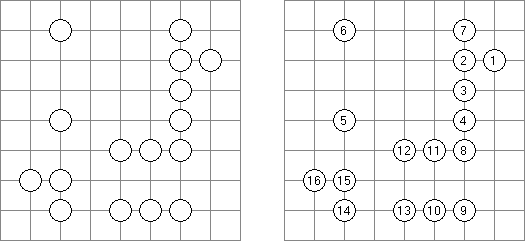
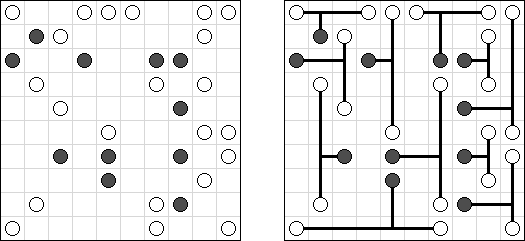
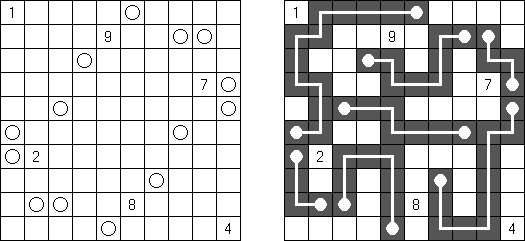
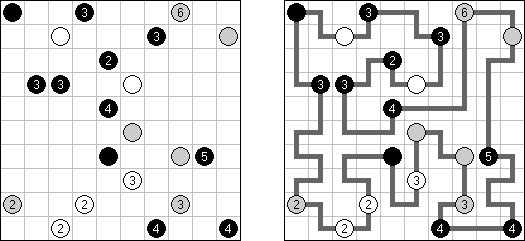
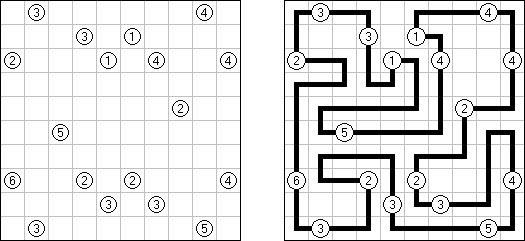
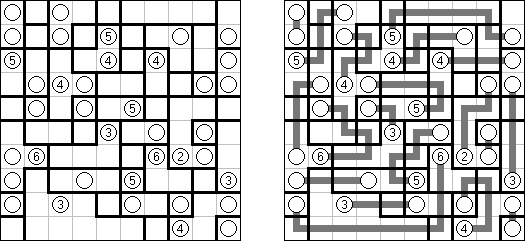
Hashiwokakero (jap. "Hashi o kakero"; wörtlich: "Brücken bauen!"; auch bekannt als "Hashi", "Brückenbau", "Bridges", "Chopsticks" oder "Ai-Ki-Ai") ist ein logisches Puzzle. Es wird auf einem rechteckigen Gitter von beliebiger Größe gespielt, wobei das Gitter selbst üblicherweise nicht gezeichnet wird. Einige Zellen sind mit Zahlen (üblicherweise eingekreist) von 1 bis 8 beschriftet; das sind die Inseln. Der Rest der Zellen ist leer.

Ziel ist es, alle Inseln zu einer einzigen Gruppe zu verbinden, indem eine Reihe von Brücken zwischen den Inseln eingezeichnet werden. Die Brücken müssen folgende Bedingungen erfüllen:

• Sie müssen auf verschiedenen Inseln beginnen und enden und dazwischen eine gerade Linie bilden.
• Sie dürfen weder eine andere Brücke noch eine andere Insel kreuzen.
• Sie dürfen nur waagrecht oder senkrecht verlaufen.
• Höchstens zwei Brücken verbinden ein Inselpaar.
• Die Anzahl der Brücken, die auf eine Insel führen, entspricht der Zahl auf dieser Insel.

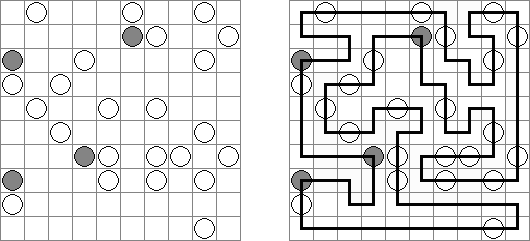
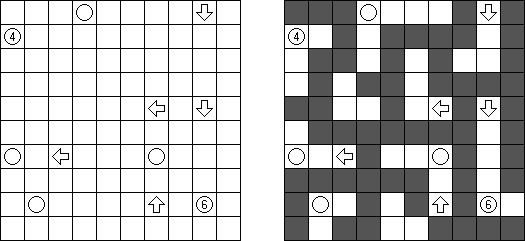
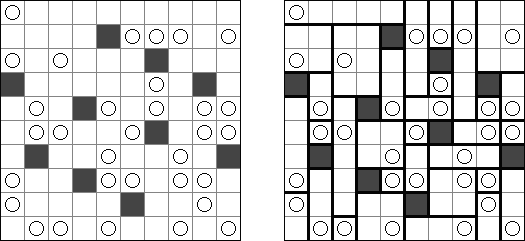
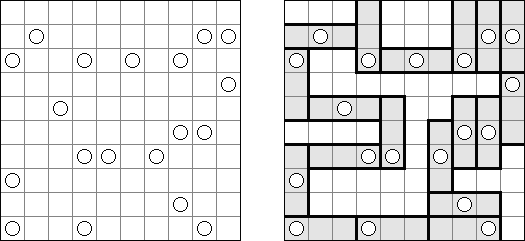
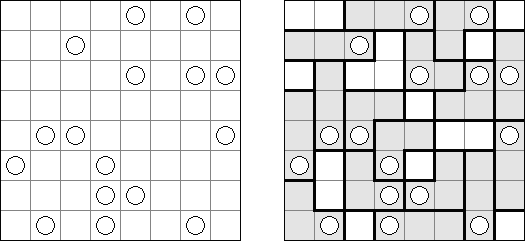
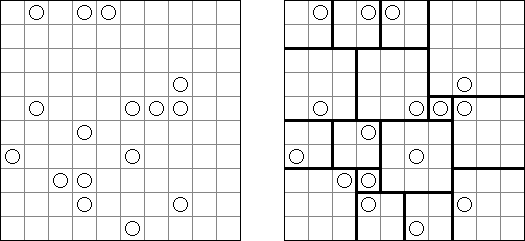
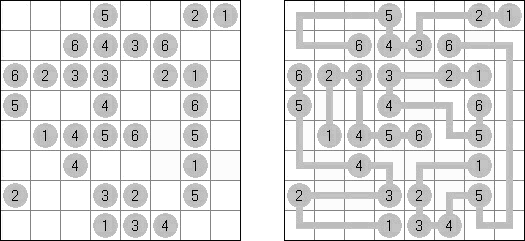
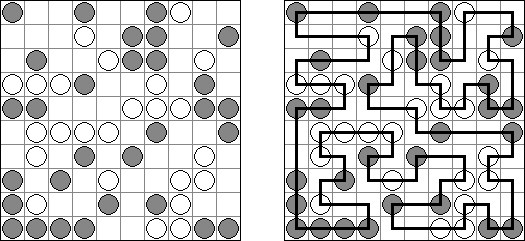
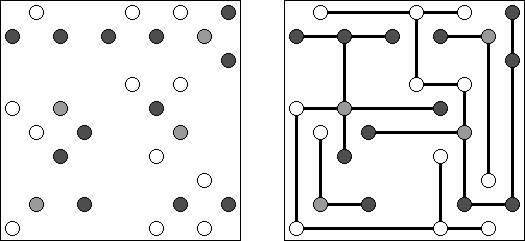
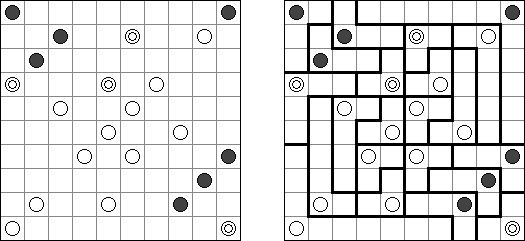
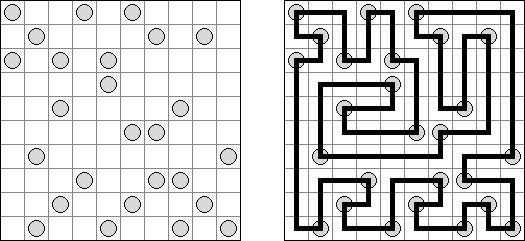
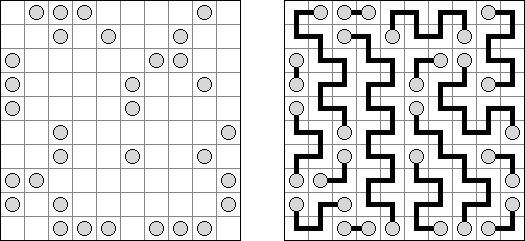
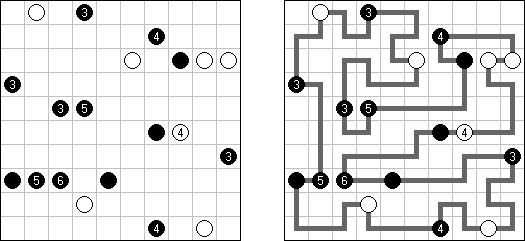
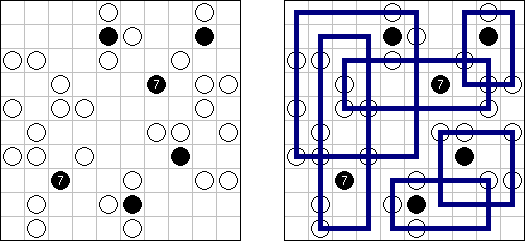
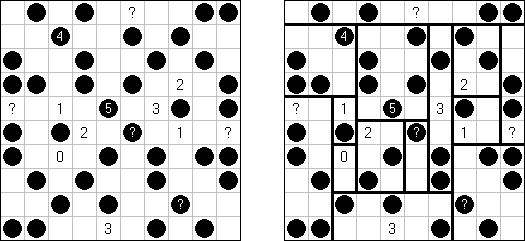
Masyu (dt. "schlechter Einfluss", auch bekannt als "Perlenkette", "Pfadfinder", "Knickwege", "Shiroshinju Kuroshinju", "White Pearls and Black Pearls") ist ein logisches Puzzle. Es wird auf einem rechteckigen Gitter gespielt, bei dem einige Quadrate Kreise enthalten; jeder Kreis ist entweder "weiß" (leer) oder "schwarz" (gefüllt). Ziel ist es, einen geschlossenen Weg zu zeichnen, der durch alle Zellen mit Kreisen führt. Der Weg muss jede Zelle, die er passiert, von der Mitte einer der vier Seiten betreten und an einer anderen Kante austreten; alle Abbiegungen haben 90 Grad.

Die beiden Kreisvarianten haben unterschiedliche Bedingungen, wie der Weg durch sie passieren muss:

• Durch weiße Kreise muss man geradeaus wandern, aber der Weg muss in der vorhergehenden oder nächsten Zelle seine Richtung ändern.
• Schwarze Kreise müssen auf einer Abbiegung um 90 Grad liegen, aber der Weg muss durch die nächste und vorhergehende Zelle in gerader Linie verlaufen.

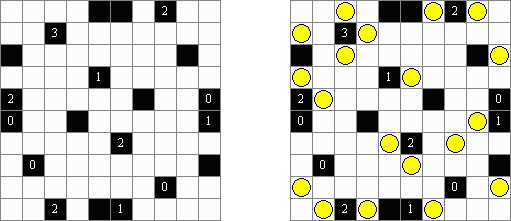
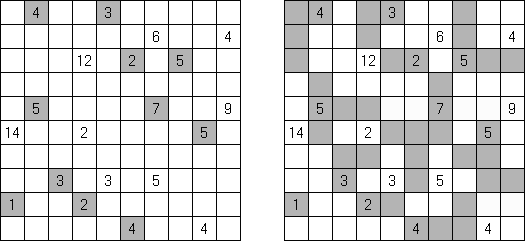
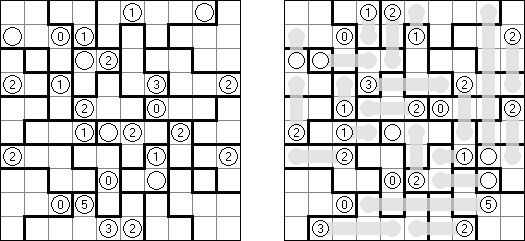
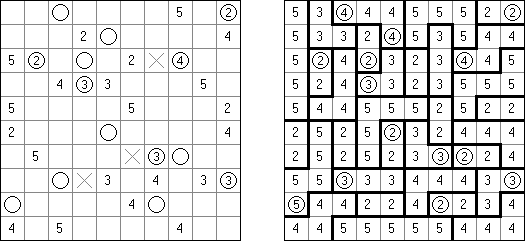
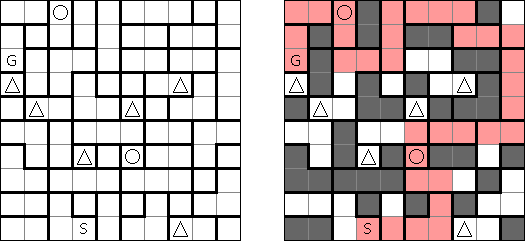
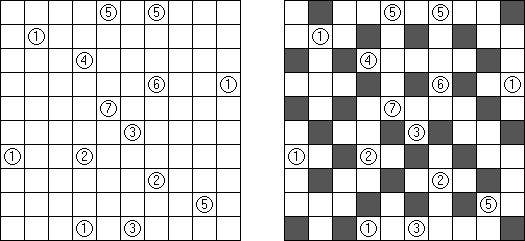
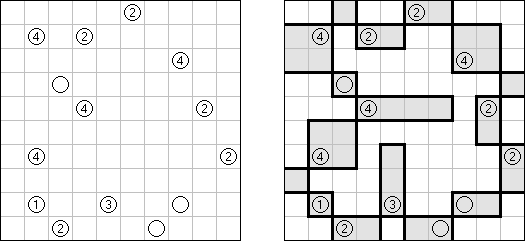
Beleuchtung (auch bekannt als "Light Up", "Akari", "Bijutsukan") ist ein logisches Puzzle. Es wird in einem rechteckigen Rastergitter mit weißen und schwarzen Feldern gespielt. Der Spieler platziert Lampen in weißen Feldern derart, dass Lampen nicht aufeinander gerichtet sind, bis das gesamte Rastergitter beleuchtet ist. Eine Lampe beleuchtet eine gesamte Reihe (horizontal) und Spalte (vertikal), wenn sie nicht durch ein schwarzes Feld blockiert wird. Ein schwarzes Feld kann eine Zahl von 0 bis 4 haben, welche anzeigt, wie viele Lampen an ihre vier Seiten anschließen sollen; z.B. muss ein Feld mit einer 4 vier Lampen anschließend haben, eine auf jeder Seite, und ein Feld mit einer 0 darf keine Lampe an irgendeiner Seite haben. Ein schwarzes Feld ohne Zahl kann jede Anzahl von Lampen drum herum haben, oder gar keine. Lampen, die diagonal eines nummerierten Feldes angebracht sind, werden in der Lampenzählung nicht berücksichtigt.

Fillomino (auch bekannt als "Polyominous") ist ein logisches Puzzle. Es wird in einem quadaratischen Rastergitter gespielt. Einige Quadrate enthalten Zahlen. Ziel ist, das Rastergitter in Blöcke zu unterteilen. Ein Block muss genau die Anzahl der Quadrate enthalten, die durch die Zahl in den Quadraten des Blocks angegeben wird. Ein Block darf keinen Block gleicher Größe horizontal oder vertikal berühren. Quadrate ohne Zahlen können Blöcke bilden, die nötig sind, um das Puzzle zu vervollständigen.

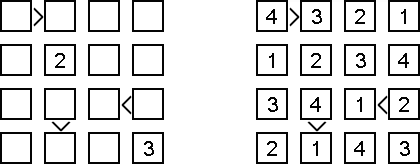
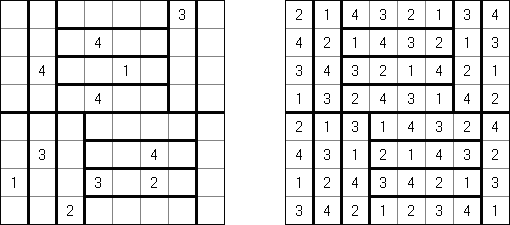
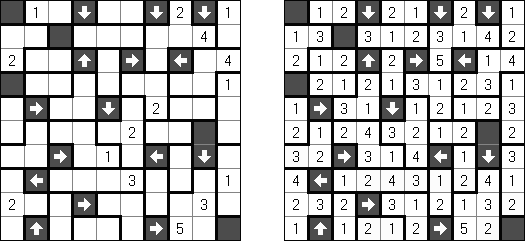
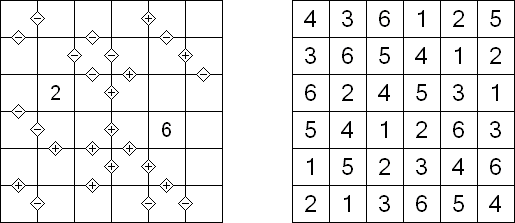
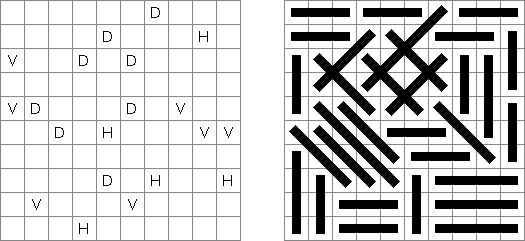
Futoshiki (auf japanisch; wörtlich: "Nicht gleich"; auch bekannt als "Hutoshiki", "Unequal") ist ein logisches Puzzle. Das Puzzle wird auf einem quadratischen Gitter gespielt, z.B. 9 x 9. Die Aufgabe besteht darin, in jeder Reihe die Zahlen 1 bis 9 (oder einer anderen Größenordnung) so zu platzieren, dass auch jede Spalte die Zahlen 1 bis 9 enthält. Einige Zahlen können bereit vorgegeben sein. Zusätzlich sind zu Beginn zwischen einigen Feldern Relationszeichen eingetragen, die anzeigen, ob eine Zahl größer oder kleiner als ihre Nachbarzahl sein soll. Diese Bedingungen müssen beim Ausfüllen des Diagramms berücksichtigt werden.

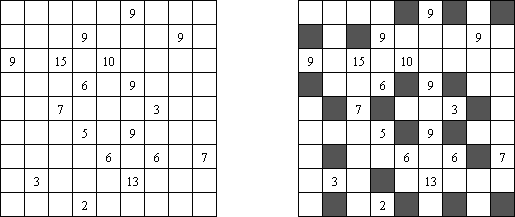
Kuromasu (auf japanisch: "kuromasu wa doko da", wörtlich: "Wo sind schwarze Zellen?"; auch bekannt als "Kurodoko") wird auf einem quadratischen Gitter gespielt. Einige der Zellen enthalten Zahlen. Jede Zelle ist entweder schwarz oder weiß. Die Aufgabe besteht darin herauszufinden, welcher Art jede Zelle ist.

Die folgenden Regeln bestimmen, welcher Art eine Zelle ist:

• Jede Zahl im Spielfeld repräsentiert die Anzahl der weißen Zellen, die von dieser Zelle aus gesehen werden können, einschließlich der Zelle selbst. Eine Zelle kann von einer anderen Zelle aus gesehen werden, wenn sie sich in der gleichen Reihe oder Spalte befindet und keine schwarzen Zellen in dieser Reihe oder Spalte dazwischen liegen.
• Zellen mit Zahlen können nicht schwarz sein.
• Schwarze Zellen dürfen horizontal oder vertikal nicht aneinander hängen.
• Alle weißen Zellen müssen horizontal oder vertikal verbunden sein.

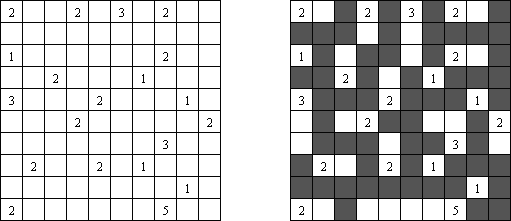
Nurikabe ist ein logisches Puzzle ("Nurikabe" bedeutet in der japanischen Folklore eine unsichtbare Mauer, die Straßen blockiert und für Verzögerungen bei Fußreisen verantwortlicht gemacht wird; andere Namen für das Puzzle: "Cell Structure", "Islands in the Stream"). Das Puzzle wird üblicherweise auf einem rechteckigen Gitter ohne bestimmte Standardgröße gespielt. Zu Beginn haben einige Felder des Gitters Zahlen.

Ziel ist es zu entscheiden, ob eine Zelle des Gitters "schwarz" oder "weiß" ist entsprechend folgender Regeln:

• Alle schwarzen Zellen müssen miteinander verbunden sein.
• Jede nummerierte Zelle muss Teil einer weißen Insel von miteinander verbundenen weißen Zellen sein.
• Jede Insel muss die gleiche Anzahl von weißen Zellen haben, wie die darin enthaltene Nummer angibt (einschließlich der nummerierten Zelle).
• Zwei Inseln dürfen nicht verbunden sein.
• Es dürfen keine 2 x 2 Blöcke schwarzer Zellen vorkommen.

Sashikabe verbindet die Regeln des Nurikabe und des Sashigane Puzzles. Das Ziel ist, einige Felder eines Rastergitters nach den folgenden Regeln zu schwärzen:

• Alle schwarzen Felder müssen miteinander verbunden sein.
• Es dürfen keine 2 x 2 Blöcke von schwarzen Feldern vorkommen.
• Alle Inseln müssen L-förmig und ein Feld breit sein. Zwei Inseln dürfen nicht verbunden sein.
• Ein Kreis markiert ein Feld, in dem ein "L" eine Biegung hat.
• Eine Insel muss die gleiche Anzahl von weißen Feldern haben wie die Zahl in dem Kreis.
• Ein Pfeil markiert das Ende eines "Beins" der Insel; der Pfeil zeigt auf das Feld, in dem das "L" die Biegung hat.

Yajikabe wurde von Naoki Inaba (Japan) erfunden: Er kombinierte Yajilin und Nurikabe-Rätsel. Ziel ist es, einige Felder eines Rastergitters nach den folgenden Regeln zu schwärzen:

• Felder mit Zahlen sind immer weiß.
• Kein Bereich von 2 x 2 Feldern innerhalb des Rastergitters darf nur schwarze Felder enthalten.
• Alle schwarzen Felder bilden einen zusammenhängenden Bereich.
• Ein Feld, das eine Zahl und einen Pfeil enthält, gibt an, wie viele schwarze Felder sich in der Zeile oder Spalte befinden, auf die der Pfeil zeigt.

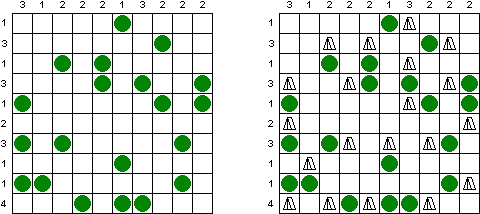
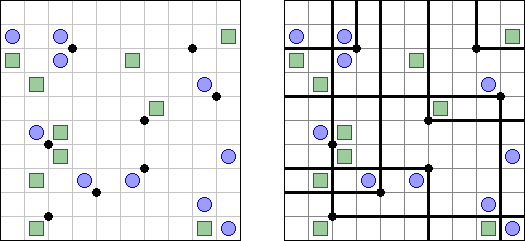
Zeltlager ("Tents", "Tents and Trees") wird auf einem quadratischen Gitter gespielt, in welchem einige Felder Bäume enthalten. Das Ziel ist, Zelte so in einige der übrigen Quadrate zu setzen, dass die folgenden Bedingungen erfüllt sind:

• Es gibt genauso viele Zelte wie Bäume.
• Die Zelte und Bäume können so zugeordnet werden, dass jedes Zelt direkt mit seinem zugehörigen Baum verbunden werden kann (horizontal oder vertikal, aber nicht diagonal). Ein Zelt kann allerdings außer mit seinem eigenen Baum auch mit einem anderen Baum benachbart sein.
• Zwei Zelte dürfen werder horizontal noch vertikal oder diagonal benachbart sein.
• Die Anzahl der Zelte in jeder Reihe und in jeder Spalte müssen mit den Zahlen übereinstimmen, die an den Rändern des Gitters angegeben sind.

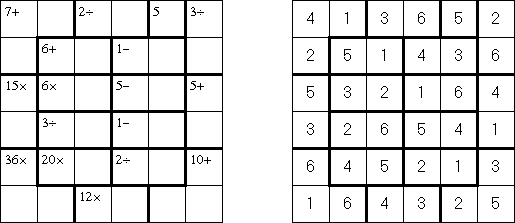
Calcudoku ("Ken Ken", "KENKEN", "KenDoku", "Square Wisdom") ist ein mathematisches und logisches Puzzle ähnlich Sudoku. Es wurde von dem japanischen Mathematik-Lehrer Tetsuya Miyamoto erfunden. Die Aufgabe besteht darin, das Rastergitter mit den Zahlen 1 bis N (wobei N die Anzahl der Reihen oder Spalten im Rastergitter ist) in der Weise zu füllen, dass:

• Jede Reihe genau eine der Zahlen enthält.
• Jede Spalte genau eine der Zahlen enthält.
• Jeder dick umrandete Block enthält Zahlen, welche das angegebene Ergebnis erbringen, nachdem man die angegebene mathematische Operation angewandt hat: Addition (+), Subtraktion (-), Multiplikation (×) und Division (÷).
• Im Unterschied zu Summen-Sudoku dürfen sich Zahlen innerhalb eines Blockes wiederholen.

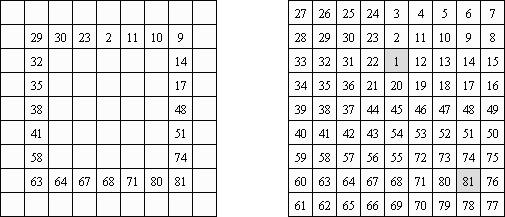
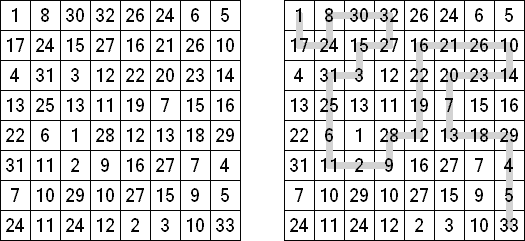
Hidato (von hebräisch: "Mein Puzzle"; auch bekannt als "Hidoku") ist ein Puzzle, das von dem israelischen Mathematiker Gyora Benedek erfunden wurde. Das Ziel von Hidato ist, das Spielfeld mit fortlaufenden Zahlen zu füllen, die horizontal, vertikal oder diagonal verbunden sind. In jedem Hidato Puzzle werden die größte und die kleinste Zahl im Spielfeld angezeigt. Weitere Zahlen im Spielfeld sollen dem Spieler Hinweise geben, wie er beginnen kann, die Lösung zu finden, und um sicherzustellen, dass Hidato nur eine einzige Lösung hat.

Numbrix ist ein logisches Puzzle. Es wird in einem rechteckigen Spielfeld mit Quadraten gespielt. Einige der Felder enthalten Zahlen. Ziel ist, die fehlenden Zahlen in fortlaufender Folge horizontal oder vertikal einzusetzen. Diagonale Pfade sind nicht erlaubt.

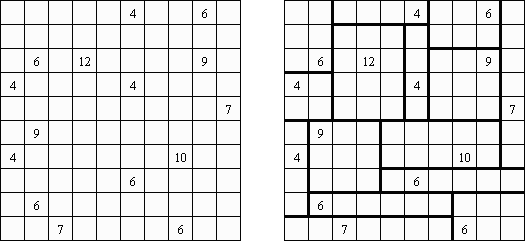
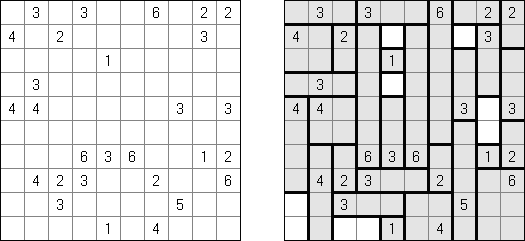
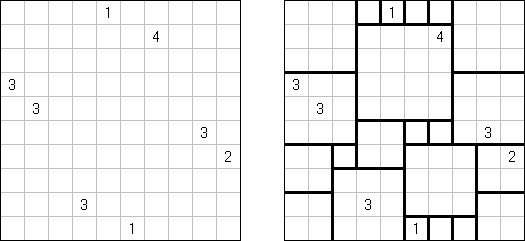
Shikaku (auch bekannt als "Divide by Squares", "Divide by Box", "Number Area") ist ein logisches Puzzle. Es wird auf einem rechteckigen Rastergitter gespielt. Einige Felder im Spielfeld sind nummeriert. Ziel ist, das Spielfeld so in rechteckige und quadratische Bereiche zu zerlegen, dass jeder Bereich genau eine Zahl enthält und die Zahlen die Größe des Rechtecks repräsentieren.

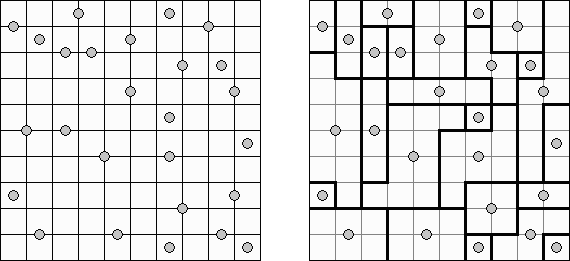
Galaxien (auch bekannt als "Tentai Show", "Sym-a-Pix") befinden sich in einem rechteckigen Rastergitter mit Punkten. Ziel ist es, zu jedem Punkt genau eine punktsymmetrische Region (Galaxie) zu bilden. Dabei dürfen sich die verschiedenen Galaxien nicht überschneiden und keine Leerräume bilden.

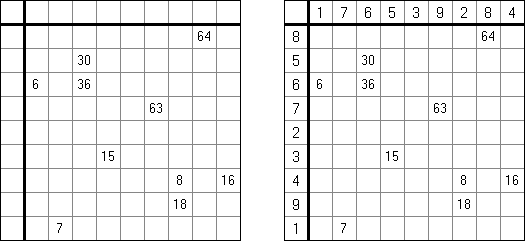
Wolkenkratzer (auch bekannt als "Skyscrapers", "Hochhäuser") besteht aus einem quadratischen Gitter. Ziel ist es, jedes Feld mit Zahlen von 1 bis N zu füllen, wobei N die Größe der Puzzle-Seite ist. Keine Zahl darf zweimal in einer Reihe oder Spalte vorkommen. Die Zahlen um den Rand des Puzzles zeigen die Anzahl von Gebäuden an, welche Sie von dieser Seite aus sehen könnten, wenn da eine Reihe von Wolkenkratzern wäre, deren Höhe gleich der Einträge in dieser Reihe oder Spalte sind.

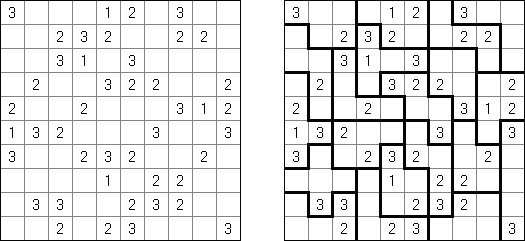
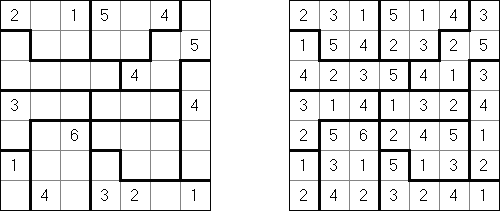
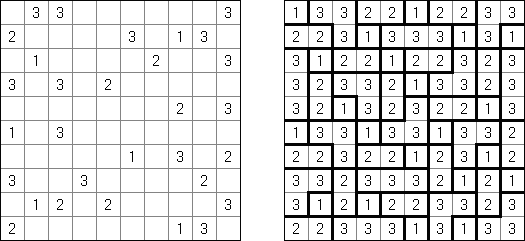
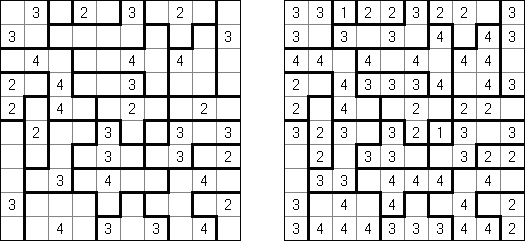
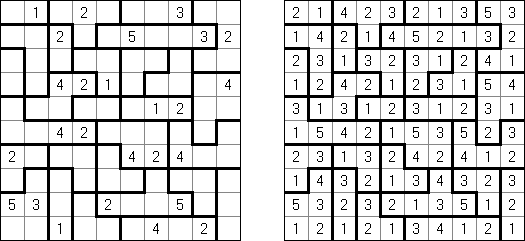
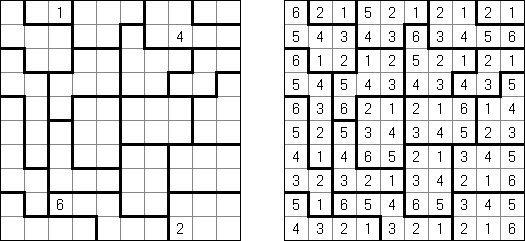
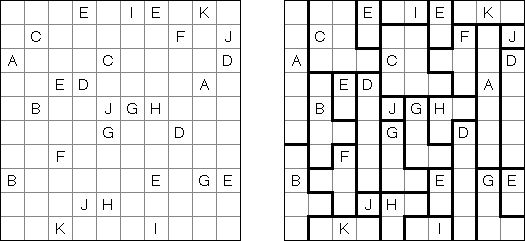
Hakyuu (auch bekannt als "Ripple Effect", "Hakyuu Kouka", "Hakyukoka", "Seismic") ist ein logisches Puzzle. Es besteht aus einem rechteckigen Raster beliebiger Größe, welches in Polyomino-Abschnitte, genannt "Gebiete", unterteilt ist. Jedes Gebiet muss alle Zahlen von 1 bis zur Anzahl der Felder in diesem Gebiet je einmal enthalten. Wenn zwei identische Zahlen in der gleichen Reihe oder Spalte vorkommen, müssen mindestens ebenso viele Felder mit anderen Zahlen dazwischen stehen.

Grand Tour ist ein logisches Puzzle. Es besteht aus einem Rasterfeld mit Punkten, die alle durch eine einzige Schleife miteinander verbunden werden müssen. Als Starthilfe sind einige Punkte schon miteinander verbunden, um eine eindeutige Lösung zu garantieren.

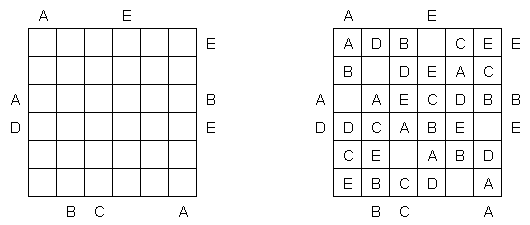
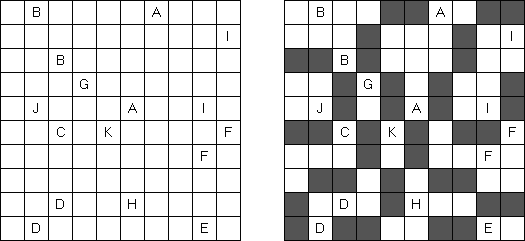
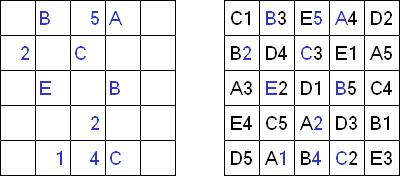
Buchstabensalat (auch bekannt als "Easy as ABC", "ABC End View", "Last Man Standing") besteht aus einem quadratischen Rastergitter, dessen Felder mit einer bestimmten Auswahl von Buchstaben gefüllt werden müssen (z.B. A bis E), wobei jeder Buchstabe genau einmal in jeder Reihe und Spalte vorkommen darf und die anderen Felder leer bleiben. Die Buchstaben außerhalb des Gitters geben an, welcher Buchstabe zuerst von dieser Richtung aus gesehen werden kann.

Regenwolken (auch bekannt als "Clouds", "Rain Clouds", "Radar") ist eine Variante des Puzzles "Marinespiel". Die Aufgabe besteht darin zu bestimmen, welche Zellen des quadratischen Rastergitters zu einer Wolke gehören. Wolken belegen ein rechteckiges Gebiet und ihre Breite und Höhe ist mindestens zwei Zellen. Keine Wolke berührt eine andere, auch nicht diagonal. Zahlen außerhalb des Rastergitters geben die Anzahl der Zellen an, die in der entsprechenden Reihe oder Spalte von Wolken belegt werden.

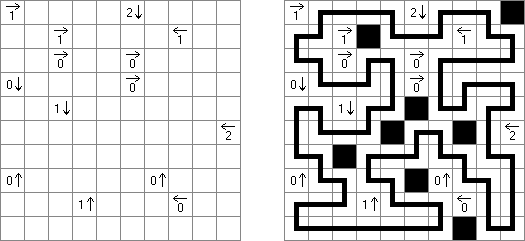
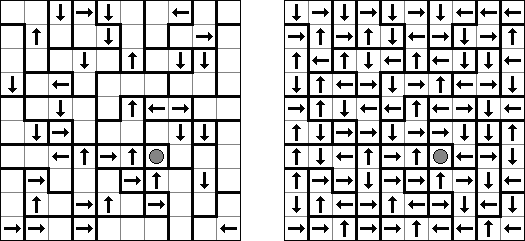
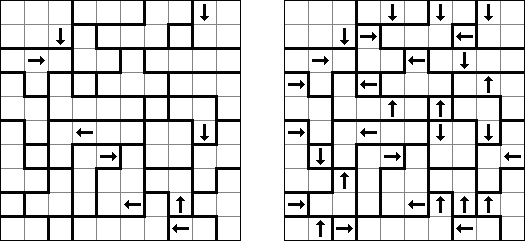
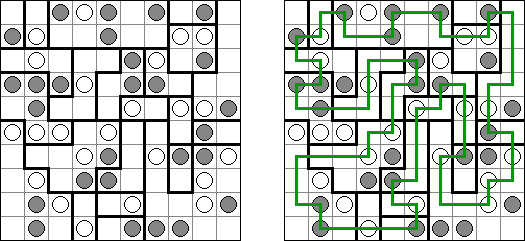
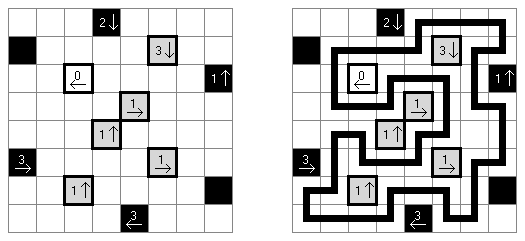
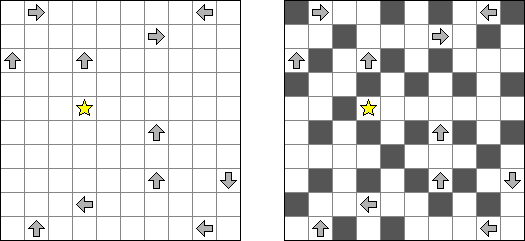
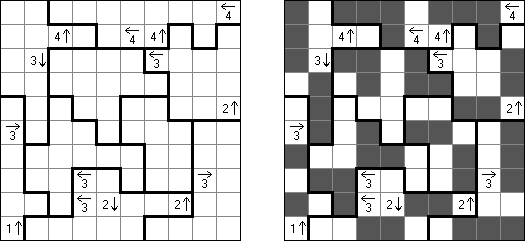
Yajilin (auch bekannt als "Arrow Ring" oder "Straight and Arrow") ist ein logisches Puzzle, das von Nikoli veröffentlicht wurde. Ziel ist, eine einzige fortlaufende, sich nicht überschneidende Schleife zu zeichnen, welche die Mittelpunkte der Felder verbindet. Dabei darf die Schleife keine Felder mit Pfeilen durchqueren; sie darf nur horizontal oder vertikal aber nie diagonal verlaufen. Jedes Feld, das keinen Pfeil enthält und nicht ein Teil der Schleife ist, muss schwarz sein. Schwarze Felder dürfen sich nicht orthogonal berühren (sie haben keine gemeinsame Seite). Ein Feld, das eine Zahl und einen Pfeil enthält, gibt an, wie viele schwarze Felder sich in der Reihe oder Spalte in Pfeilrichtung befinden. Es können schwarze Felder vorkommen, auf die nicht durch Felder mit Pfeilen und Zahlen hingewiesen wird. Das Rastergitter kann graue Felder enthalten, die nicht Teil des Rundwegs sind.

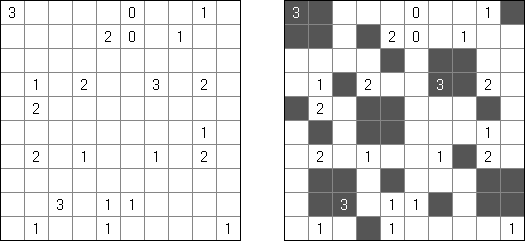
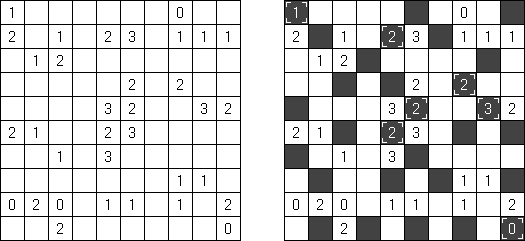
Minesweeper ("Minensuche", "Schatzsuche") ist durch das Spiel in Microsoft Windows wohlbekannt. Die Aufgabe ist hier, Minen in den leeren Feldern des Spielfeldes zu verteilen. Die Zahlen im Spielfeld repräsentieren die Anzahl der Minen in benachbarten Feldern - einschließlich diagonaler Felder.

Minensuchflotte ("Minesweeper Battleships", "Battlemines") kombiniert das Battleships Puzzle (Bimaru, Marinespiel) mit dem Minesweeper-Spiel (Mines, Minensuche), welches auf vielen Computern zu finden ist. Ziel ist es, die Position der Flotte im Rastergitter zu lokalisieren. Die Schiffe berühren sich nicht gegenseitig, auch nicht diagonal. Ein Feld mit einer Zahl gibt an, wie viele Schiffssegmente benachbart sind. Schiffe sind nicht in den nummerierten Zellen erlaubt.

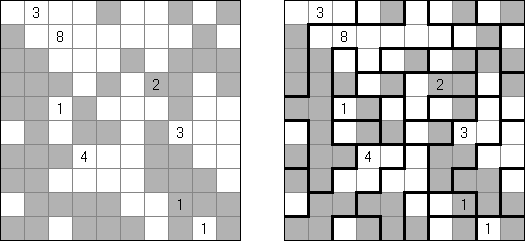
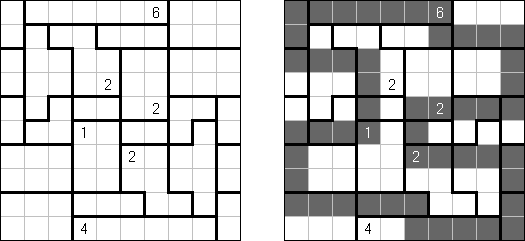
Heyawake (aus dem Japanischen, "unterteilte Zimmer") wird auf einem rechteckigen Rastergitter gespielt. Das Spielfeld ist in rechteckige "Zimmer" unterteilt. Einige Zimmer können eine einzelne Zahl enthalten. Diese Zimmer müssen die angegebene Anzahl von schwarzen Feldern enthalten. Andere Zimmer können keine oder mehr schwarze Felder enthalten.

• Schwarze Felder dürfen nicht orthogonal verbunden sein.
• Alle weißen Felder müssen verbunden sein.
• In einer Reihe von verbundenen weißen Feldern dürfen nicht mehr als zwei Zimmer miteinander verbunden sein.

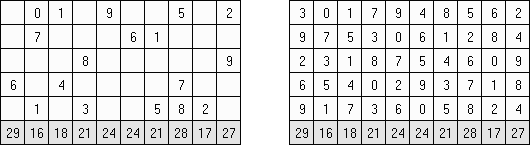
Zehnergitter (auch bekannt als "Tenner Grid", "From 1 to 10", "Grid Ten") besteht aus einem rechteckigen Rastergitter mit einer Weite von zehn Feldern. Aufgabe ist es, das Rastergitter so auszufüllen, dass jede Reihe die Zahlen von 0 bis 9 enthält. In den Spalten können sich Zahlen wiederholen. Die Zahlen in der unteren Reihe geben jeweils die Summe der Zahlen in der Spalte an. Die Zahlen in angrenzenden Feldern (auch in diagonal angrenzenden Feldern) müssen unterschiedlich sein.

Hundert ("Hundred") ist ein quadratisches Rastergitter von 3 x 3 oder 4 x 4, dessen Felder mit einigen Zahlen gefüllt werden sollen. Die Aufgabe besteht darin, zusätzliche Zahlen in die gefragten Felder zu setzen, so dass die Summe der Zahlen in jeder Reihe und jeder Spalte gleich hundert ist.

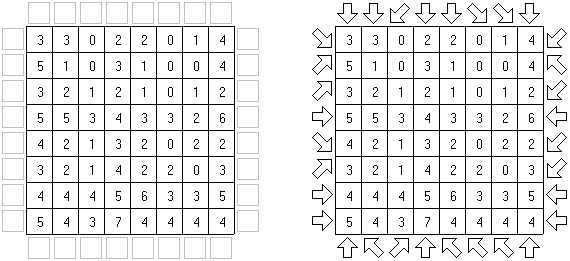
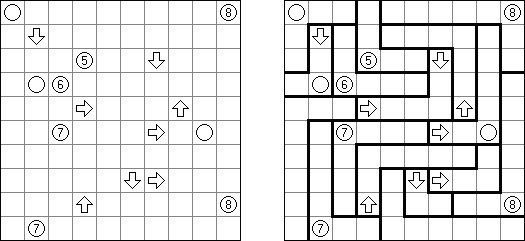
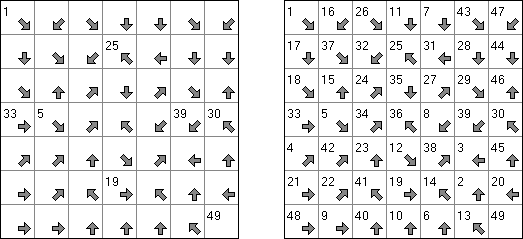
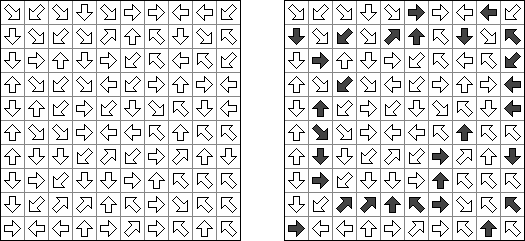
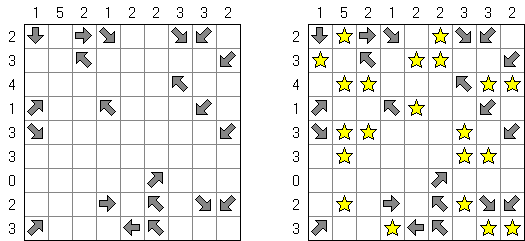
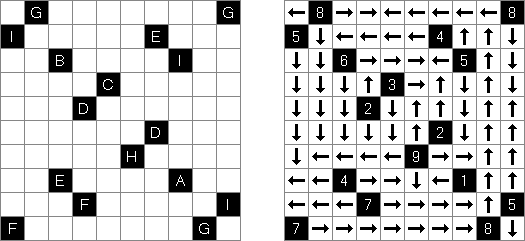
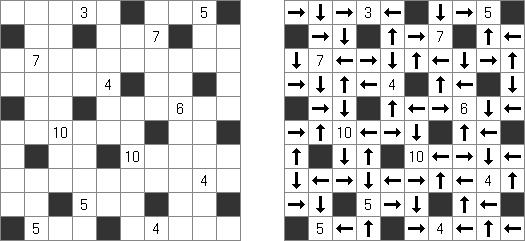
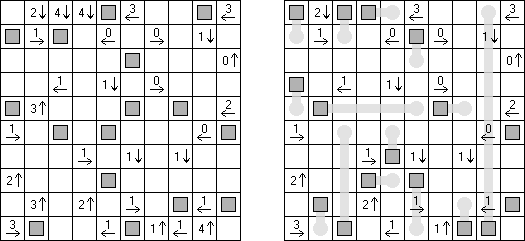
Pfeilzahlen (auch bekannt als "Arrows" oder "Pfeile") ist ein logisches Puzzle. Es wird in einem rechteckigen Rastergitter gespielt, das mit Zahlen gefüllt ist. Die Aufgabe besteht darin, Pfeile außerhalb des Gitters zu platzieren. Jeder Pfeil kann horizontal, vertikal oder diagonal verlaufen und zeigt mindestens auf ein Feld mit einer Zahl. Die Zahlen geben die Gesamtzahl aller Pfeile, die auf sie zeigen, an.

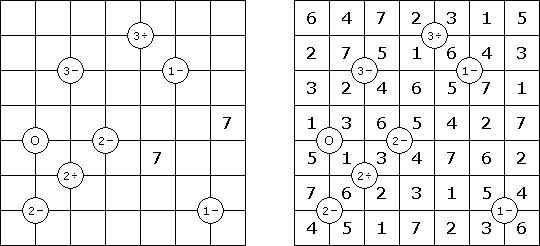
Mathrax besteht aus einem quadratischen Rastergitter. Ziel ist es, in jedes Feld die Zahlen 1 bis N einzutragen, wobei N gleich der Größe des Rastergitters ist. Keine Zahl darf zweimal in einer Zeile oder Spalte vorkommen. Kreise mit zusätzlichen Bedingungen können sich auf Schnittpunkten der Linien innerhalb des Rasters befinden; ein Kreis kann enthalten:

• Eine Zahl und ein Zeichen einer mathematischen Operation (Addition, Subtraktion, Multiplikation, Division) - die Zahl ist das Ergebnis der Rechenoperation zweier Zahlen in diagonal benachbarten Zellen.
• Ein Buchstabe "E" ("even" - "gerade") - alle Zahlen in vier Zellen sind gerade.
• Ein Buchstabe "O" ("odd" - "ungerade") - alle Zahlen in vier Zellen sind ungerade.

Str8ts (auch als "Straights" bekannt) ist ein logisches Puzzle und wurde von Jeff Widderich (Kanada) erfunden. Es ist ein quadratisches Rastergitter, welches durch schwarze Felder in Kompartimente aufgeteilt wird. Zusammenhängende weiße Felder müssen vertikal oder horizontal eine "Straße" (straight) - eine Reihe von aufeinander folgenden Zahlen, aber in beliebiger Reihenfolge - bilden. Dabei darf in keiner Zeile oder Spalte eine Zahl wiederholt vorkommen. Lösungen in schwarzen Feldern streichen diese Zahl als Option in dieser Reihe oder Spalte und sind nicht Teil einer "Straße".

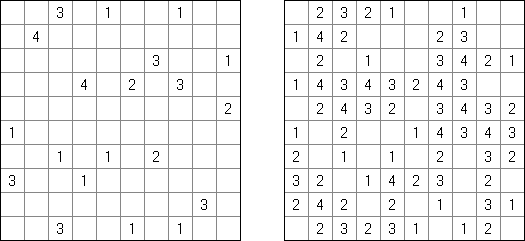
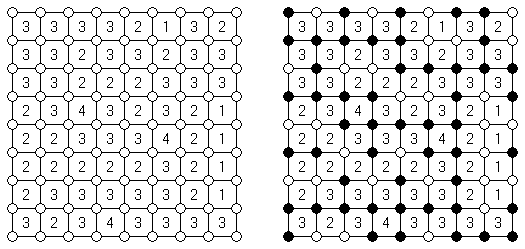
Linesweeper wird auf einem rechteckigen Rastergitter gespielt. Die Aufgabe besteht darin, eine fortlaufende und nicht-schneidende Schleife zu bilden, die die Mittelpunkte der Felder verbindet. Dabei dürfen die nummerierten Felder nicht durchquert werden; die Zahl in einem Feld gibt an, wie viele der 8 umgebenden Felder vom gesuchten Pfad durchquert werden. (Zum Beispiel bedeutet "0", dass alle 8 umgebenden Felder nicht durchquert werden dürfen).

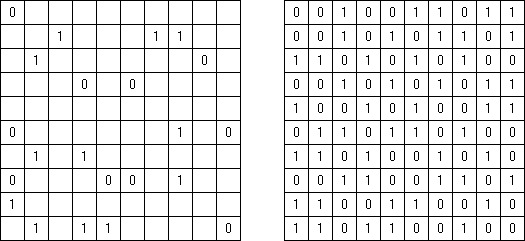
Binairo (auch bekannt als "Binary Puzzle", "Eins und Zwei", "Takuzu", "Tohu wa Vohu") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Ziel ist es, das Rastergitter mit den Zahlen "0" und "1" entsprechend der folgenden Regeln zu füllen:

• In jeder Reihe und Spalte gibt es die gleiche Anzahl der Ziffern "0" und "1".
• In einer Reihe dürfen nicht mehr als zwei Felder die gleiche Zahl enthalten.
• Jede Reihe ist einzigartig und jede Spalte ist einzigartig.

Mauerbau ("Walls") ist ein logisches Puzzle, welches von Naoki Inaba (Japan) erfunden wurde. Die Aufgabe besteht darin, in jedes weiße Feld eine horizontale oder vertikale Linie zu zeichnen. Dabei bezeichnet jede Zahl in einem schwarzen Feld die Gesamtlänge aller Segmente, die mit diesem Quadrat verbunden sind.

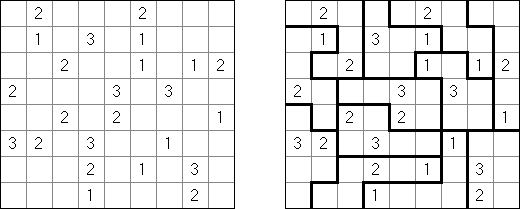
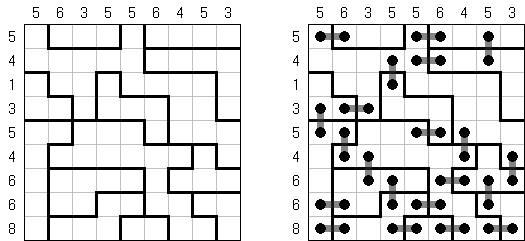
Dominos ("Dominosa", "Dominosuche", "Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") ist ein logisches Puzzle. Auf dem Spielfeld sind die Domino-Zahlen sichtbar, aber die Begrenzungen zwischen den Domino-Steinen fehlen. Aufgabe ist es, die Grenzen zwischen den Domino-Steinen wiederherzustellen.

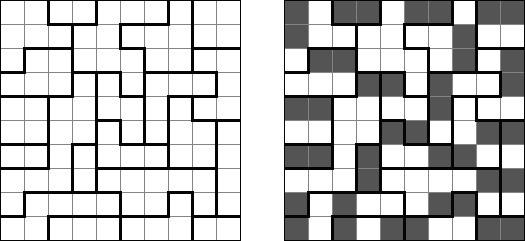
Patchwork (auch bekannt als "Tatami") besteht aus einem quadratischen Rastergitter, welches in Blöcke ("Zimmer") unterteilt ist. Jedes Zimmer muss mit den Ziffern von 1 bis zur Anzahl der Zellen des Zimmers gefüllt werden. Dabei müssen jede Zeile und jede Spalte die gleiche Anzahl von jeder Ziffer enthalten. Gleiche Ziffern dürfen nicht orthogonal benachbart sein.

In einigen Puzzles werden Buchstaben anstelle von Zahlen verwendet. Cross+A kann solche Puzzles ebenso lösen.

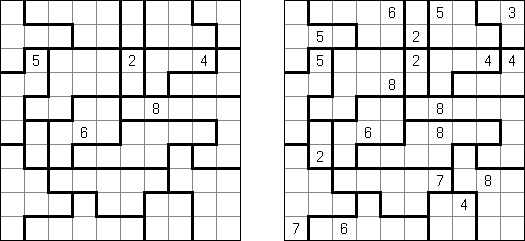
Knossos ist ein logisches Puzzle ("Knossos" ist ein Palast auf Kreta, welcher mit alten Legenden wie dem Mythos vom Labyrinth und dem Minotaurus verbunden ist). Es wird auf einem rechteckigen Rastergitter gespielt. Einige der Felder im Spielfeld sind nummeriert. Ziel ist es, das Rastergitter so in Regionen (Zimmer) aufzuteilen, dass jede Region genau eine Zahl enthält, welche die Länge der Begrenzungen des Rechtecks repräsentiert.

Rekuto ("Recto") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Einige Felder enthalten Zahlen. Die Aufgabe besteht darin, das Rastergitter so in rechteckige und quadratische Teile zu zerlegen, dass jedes Stück genau eine Zahl enthält, welche die Summe der Breite und Höhe des Rechtecks repräsentiert.

Nachbarn ("Neighbours") wird in einem Rastergitter mit unregelmäßigen Formen gespielt. Einige Felder des Spielfelds enthalten Zahlen. Das Spielfeld soll in eine Anzahl verbundener Regionen mit jeweils gleicher Anzahl von Feldern zerlegt werden. Jede Region enthält genau ein Feld mit einer Zahl (oder einem Fragezeichen) und hat so viele Nachbarn, wie von der Zahl angezeigt. Regionen sind Nachbarn, wenn sie einen Teil ihrer Grenzen gemeinsam haben.

Vier Winde ("Four Winds", "Linienspiel", "Line Game") wird auf einem rechteckigen oder quadratischen Rastergitter mit schwarzen und weißen Feldern gespielt. Alle schwarzen Felder enthalten Zahlen. Ziel ist es, in jedes weiße Feld eine horizontale oder eine vertikale Linie zu zeichnen. Jede Zahl gibt die Gesamtzahl der weißen Felder an, die mit Linien ausgehend von dieser Nummer durchzogen sind. Linien dürfen nicht durch andere nummerierte schwarze Felder gehen oder sich mit anderen Linien schneiden.

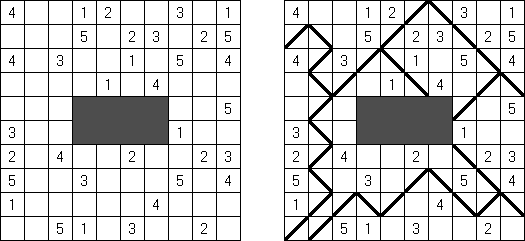
Shakashaka (auch bekannt als "Proof of Quilt") ist ein Logikrätsel, welches von Nikoli erfunden wurde. Die Aufgabe besteht darin, je eins der vier gleichschenkligen rechtwinkligen Dreiecke in einige weiße Felder zu platzieren. Dabei muss jedes Dreieck genau die Hälfte seines Feldes belegen, kann sich aber in einer von vier Ausrichtungen befinden. Jeder zusammenhängende weiße Bereich muss ein Rechteck oder Quadrat ergeben. Eine Zahl in einem schwarzen Feld zeigt an, wie viele Dreiecke an die Seiten des Feldes angrenzen.

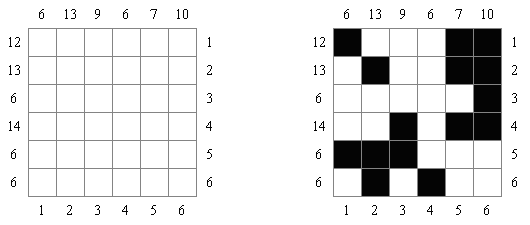
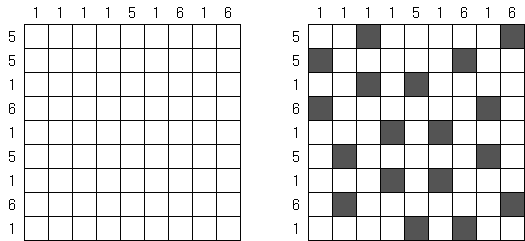
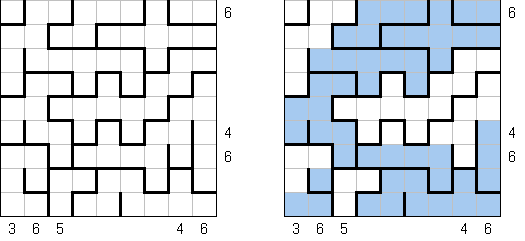
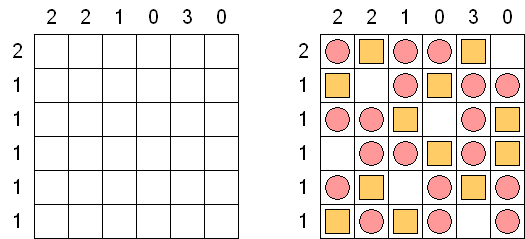
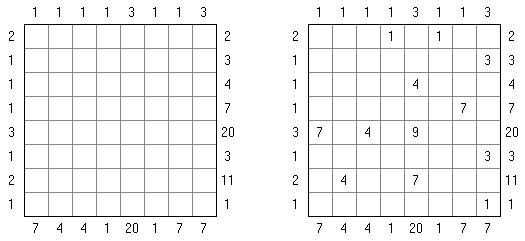
Kakurasu (auch bekannt als "Feldersummenrätsel", "Index Sums") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Das Ziel ist, einige Felder zu färben, um die Hinweise zu erfüllen. Die Zahlen am oberen und linken Rand sind die Hinweise, welche der Summe der Werte der schwarzen Felder in Reihe und Spalte entsprechen. Die Zahlen am rechten und unteren Rand sind die Werte von jedem Feld in der Reihe und Spalte. (Das erste Feld in einer Reihe oder Spalte hat den Wert 1, das zweite 2, das dritte 3, usw.)

Mochikoro ("Mochinuri") ist ein logisches Puzzle. Es besteht aus einem Rastergitter, welches in einigen Feldern Zahlen enthält. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder unterteilen das Rastergitter in rechteckige Gebiete ("Inseln") bestehend aus weißen Feldern.
• Inseln dürfen keine gemeinsamen Ränder haben, jedoch müssen alle Inseln über ihre Ecken miteinander verbunden sein.
• Jedes Feld mit einer Zahl muss zu einer weißen Insel gehören. Es können auch weiße Gebiete ohne Feld mit einer Zahl vorkommen.
• Jede Insel muss die gleiche Anzahl von weißen Feldern haben wie die Zahl, die enthalten ist (einschließlich des nummerierten Feldes).
• Es darf im Rastergitter kein Bereich mit 2 x 2 Feldern vorkommen, der nur schwarze Felder enthält.

Türen ("Offene Türen", "Doors", "Seethrough", "Open Office") ist ein logisches Puzzle, bei dem jedes Feld einen "Raum" bezeichnet. Ziel ist es, einige "Türen" zwischen Räumen zu schließen. Offene Türen erlauben es, in andere Räume zu sehen. Die Zahl in einem Feld gibt die Gesamtzahl der Zimmer an, die in horizontaler und vertikaler Richtung von diesem Raum aus sichtbar sind (ausgeschlossen der Raum selbst). Es darf keine isolierten Räume geben; das heißt, es muss möglich sein, alle Zimmer durch horizontale und vertikale Bewegung zu erreichen.

Leuchttürme ("Lighthouses") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Es enthält schwarze Felder mit Zahlen ("Leuchttürme"). Die Zahl im schwarzen Feld steht für die Anzahl von Schiffen, die der Leuchtturm beleuchtet. Ein Schiff wird beleuchtet, wenn es sich in der gleichen Zeile oder Spalte wie der Leuchtturm befindet, auch wenn sich das Schiff hinter anderen Schiffen oder Leuchttürmen befindet. Jedes Schiff wird von mindestens einem Leuchtturm beleuchtet. Die Schiffe werden so platziert, dass kein Schiff ein anderes Schiff oder einen Leuchtturm berührt, auch nicht diagonal.

Leuchttürme-Marinespiel ("Lighthouse Battleships") kombiniert das Marinespiel mit dem Leuchttürme Puzzle. Ein Feld mit einer Zahl ist ein Leuchtturm und gibt die Gesamtzahl Schiffs-Stücke an, die sich in der gleichen Zeile oder Spalte wie der Leuchtturm befinden. Weder Schiffe noch Leuchttürme dürfen einander berühren, auch nicht diagonal.

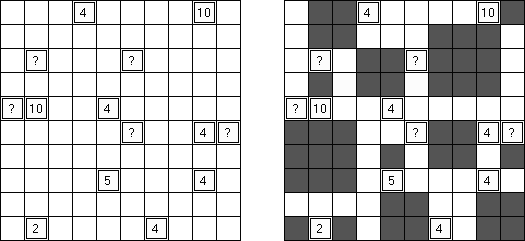
Tapa ist ein logisches Puzzle, das von Serkan Yürekli (Türkei) geschaffen wurde. Das Ziel ist, einige Felder des Rastergitters zu schwärzen. Alle schwarzen Felder bilden ein zusammenhängendes Gebiet. Keine Fläche von 2 x 2 Feldern innerhalb des Rastergitters darf ausschließlich aus schwarzen Feldern bestehen. Mit Zahlen markierte Felder sollen nicht ausgefüllt werden und geben die Länge der einzelnen aufeinander folgenden schwarzen Blöcke in den acht umliegenden Feldern an. Wenn mehr als eine Zahl in einem Feld vorkommt, müssen die Gruppen schwarzer Felder wenigstens durch ein weißes Feld getrennt werden. Fragezeichen können anstelle von Hinweiszahlen verwendet werden. Jedes Fragezeichen kann eine beliebige ganze Zahl ungleich Null repräsentieren.

Fobidoshi ("Verbotene Vier", "Forbidden Four") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Es wird auf einem quadratischen oder rechteckigen Rastergitter gespielt. In einigen Feldern befinden sich Kreise. Ziel ist es, Kreise so in leere Felder zu zeichnen, dass alle Kreise einen orthogonal zusammenhängenden Bereich bilden. Eine Reihe von verbundenen Kreisen darf nicht mehr als 3 Kreise enthalten.

Zeltinseln (auch bekannt als "Island", "Tents Island", "Airando") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Es besteht aus einem Rastergitter mit Zahlen in einigen Feldern. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die weißen Felder bilden eine einzelne Insel. Jedes nummerierte Feld muss Teil dieser Insel sein.
• Die Zahlen zeigen an, wie viele nicht nummerierte weiße Felder von diesem Feld aus durch horizontale oder vertikale Bewegung erreicht werden können. Nummerierte Felder blockieren den Zugang.

Herrschaft ("Dominion") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Es besteht aus einem Rastergitter mit Buchstaben in einigen Feldern. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder müssen Dominos bilden, die sich diagonal berühren dürfen.
• Felder mit Buchstaben sind immer weiß.
• Die schwarzen Felder unterteilen das Rastergitter in Regionen mit weißen Feldern.
• Felder mit dem gleichen Buchstaben gehören zur gleichen weißen Region.
• Weiße Regionen ohne ein Feld mit einem Buchstaben sind nicht erlaubt.

Tren ist ein logisches Puzzle, das von Shinichi Aoki (Japan) erfunden wurde. Der japanische Name dieses Puzzles bedeutet "Parken" (Jeder Block ist ein Auto und das Rastergitter ist ein Parkplatz). Das Puzzle enthält ein Rastergitter mit Zahlen in einigen Feldern. Ziel ist es, einige Blöcke mit der Größe 1 x 2 oder 1 x 3 im Rastergitter zu platzieren. Jede Zahl im Rastergitter muss Teil eines Blocks sein und die Anzahl der möglichen Bewegungen dieses Blocks anzeigen. Blöcke dürfen sich nur in Richtung ihrer kurzen Seite bewegen.

Drei in einer Reihe ("No Four in a Row") wird auf einem Rastergitter mit unregelmäßiger Form gespielt. Einige Felder des Rastergitters enthalten 'X' und 'O'. Die Aufgabe besteht darin, das Raster so auszufüllen, dass niemals vier aufeinanderfolgende identische Symbole in einer Zeile, Spalte oder Diagonale erscheinen.

Corral (auch bekannt als "Bag", "Cave") ist ein logisches Puzzle, das von Nikoli erfunden wurde. Ziel ist es, entlang der Gitterlinien eine einzige geschlossene Schleife zu zeichnen, die sich selbst nicht schneiden darf. Die Schleife umschließt alle Zahlen. Die Zahlen im Rastergitter geben an, wie viele Felder innerhalb der Schleife in horizontaler und vertikaler Sicht von diesem Feld aus gesehen werden können, einschließlich des Feldes selbst.

Foseruzu ("Vier Felder") ist ein logisches Puzzle, das von Nikoli veröffentlicht wurde. Ziel ist es, das Rastergitter in Gebiete von genau vier Feldern aufzuteilen. Die Zahl in einem Feld gibt an, wie viele seiner vier Seiten jeweils Segmente von Gebietsgrenzen sind (inklusive der Ränder des Rastergitters).

Faibuseruzu ("Fünf Felder", "Solomon's Keep"): das Rastergitter muss in Gebiete von genau fünf Feldern aufgeteilt werden.

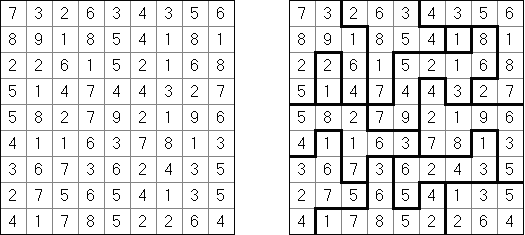
Sutoreto ("Straßenkreuz", "Sutoretokurosu", "Straight Cross") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Es wird auf einem rechteckigen oder quadratischen Rastergitter mit schwarzen und weißen Feldern gespielt. Einige weiße Felder enthalten Zahlen. Das Ziel ist, in jedem weißen Feld eine Zahl zu platzieren. Die Zahlen in einem horizontalen oder vertikalen Streifen von aufeinanderfolgenden weißen Feldern müssen eine lückenlose Folge von Zahlen bilden, aber in beliebiger Reihenfolge (zum Beispiel: 2-4-1-3).

Renban besteht aus einem quadratischen Rastergitter, das in Gebiete aufgeteilt ist. Das Ziel ist, in jedes Feld eine Zahl von 1 bis N einzutragen, wobei N die Kantenlänge des Puzzles ist. Keine Zahl darf zweimal in einer Reihe, Spalte oder einem Gebiet vorkommen. Alle Zahlen in einem Gebiet müssen eine Sequenz aufeinander folgender Zahlen bilden, können aber beliebige Reihenfolge haben (z. B.: 5-3-4).

Buraitoraito ("Strahlendes Licht", "Bright Light") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Es enthält schwarze Felder mit Zahlen. Eine Zahl gibt an, wie viele Sterne von diesem Feld aus zu sehen sind. Ein Stern ist von dem schwarzen Feld aus sichtbar, wenn er sich in der gleichen Reihe oder Spalte wie dieses Feld befindet, aber nicht hinter anderen schwarzen Feldern.

Irasuto (Illustration") ist ein Logik-Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält weiße und schwarze Felder mit Zahlen. Das Ziel ist, einige Felder des Rastergitters nach folgenden Regeln schwarz zu färben:

• Eine Zahl in einem weißen Feld gibt die Anzahl der leeren weißen Felder an, die von diesem Feld aus gesehen werden können.
• Eine Zahl in einem schwarzen Feld gibt die Anzahl der leeren schwarzen Felder an, die von diesem Feld aus gesehen werden können.

Suguru ("Number Blocks", "Zahlenblöcke") ist ein Logik-Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Die Aufgabe besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete unterteilt ist. Jedes Gebiet muss mit jeder der Zahlen von 1 bis zur Anzahl der Felder des Gebietes ausgefüllt werden. Felder mit den gleichen Zahlen dürfen nicht orthogonal oder diagonal nebeneinander liegen.

Trinudo ist ein logisches Puzzle. Es wird auf einem rechteckigen Rastergitter gespielt. Zu Beginn enthalten einige Felder des Rastergitters vorgegebene Zahlen. Ziel ist es, das Rastergitter in Bereiche von je ein, zwei oder drei Feldern zu unterteilen. Bereiche der gleichen Größe dürfen nicht orthogonal aneinanderstoßen. Jede vorgegebene Zahl bezeichnet die Größe des Bereichs, zu dem sie gehört.

Creek ("Kuriku") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Kreise mit Zahlen von 0 bis 4 können sich auf Schnittpunkten von Linien innerhalb des Rastergitters befinden. Die Zahl im Kreis gibt an, wie viele Nachbarfelder geschwärzt sein müssen. Alle weißen Felder müssen horizontal oder vertikal verbunden sein.

Gappy wird auf einem quadratischen Rastergitter gespielt. Ziel ist es, einige Felder des Rastergitters nach den folgenden Regeln zu schwärzen:

• Jede Reihe und jede Spalte enthält zwei schwarze Felder.
• Schwarze Felder dürfen einander nicht berühren, auch nicht diagonal.
• Zahlen am Rand geben die Anzahl der weißen Felder zwischen den schwarzen Feldern in der entsprechenden Reihe oder Spalte an.

Norinori ist ein logisches Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Regionen unterteilt. Das Ziel ist, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Jede Region enthält genau zwei schwarze Felder.
• Jedes schwarze Feld muss Teil eines 2 x 1 oder 1 x 2 Blocks (Dominos) sein, unabhängig von den Begrenzungen der Region.
• Zwei Dominosteine ​​dürfen keine gemeinsame Kante haben. Schwarze Blöcke dürfen einander diagonal berühren.

Yonmasu ("Yonmasubunkatsu") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise in einigen Feldern. Ziel ist es, das Rastergitter in Bereiche mit genau vier Feldern aufzuteilen. Dabei enthält jeder Bereich einen Kreis.

Ziegelmauer ("Bricks") besteht aus einem quadratischen Rastergitter. Ziel ist es, in jedes Feld eine Zahl von 1 bis N zu setzen, wobei N die Größe einer Puzzle-Seite ist. In einer Reihe oder Spalte darf keine Zahl doppelt vorkommen. Jeder Ziegelstein enthält eine ungerade und eine gerade Zahl. Halbziegel am linken und rechten Rand einer Reihe bilden gemeinsam einen ganzen Ziegel.

Zahlenschlange ("Number Chain") ist ein logisches Puzzle, das von Leonid Mochalov (Russland) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in den Feldern die Zahlen von 1 bis N. Ziel ist es, eine einzige durchgehende Linie von der oberen linken Ecke bis in die untere rechte Ecke zu ziehen. Die Linie umfasst jede Zahl von 1 bis N genau einmal.

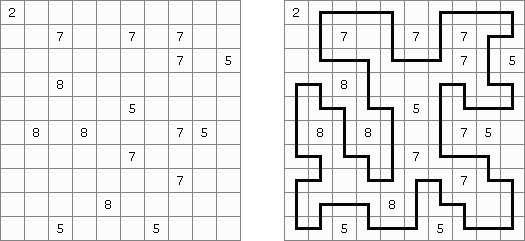
Kapetto ("Settokapetto", "Set Carpets", "Teppiche") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. In einigen Feldern sind Zahlen. Ziel ist es, das Rastergitter so in rechteckige Blöcke zu unterteilen, dass jeder Block genau eine Zahl enthält. Die Zahl repräsentiert die Anzahl der Felder in dem zugehörigen Block. Das Rastergitter kann Felder enthalten, die zu keinem Block gehören.

Renkatsu ist ein Logik-Puzzle, das von Naoki Inaba (Japan) entwickelt wurde. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt, welches mit Zahlen gefüllt ist. Die Aufgabe besteht darin, das Rastergitter in Bereiche aufzuteilen. Jeder Bereich enthält Zahlen von 1 bis zur Anzahl der Felder in diesem Bereich.

Eulero ("Griechisch-lateinisches Quadrat", "Euler Quadrat") ist ein Puzzle mit Buchstaben und Zahlen. Ziel ist es, das Rastergitter nach folgenden Regeln mit Symbolen auszufüllen:

• Jedes Feld enthält einen Buchstaben und eine Zahl.
• Jede Reihe und jede Spalte enthält jeden Buchstaben und jede Zahl genau einmal.
• Keine zwei Felder enthalten das gleiche Paar von Symbolen.

Anraikumozaiku ("Unlike Mosaic", "Ungleich-Mosaik") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise in einigen Feldern. Ziel ist es, das Rastergitter in rechteckige Regionen zu unterteilen. Dabei enthält jede Region einen Kreis. Schwarze Felder gehören zu keiner Region. Regionen gleicher Größe dürfen keine Kante gemeinsam haben.

Kurotto (aus dem Japanischen, wörtlich: "schwarze Einheiten") ist ein logisches Puzzle, das von Nikoli veröffentlicht wurde. Die Aufgabe besteht aus einem Rastergitter, welches Kreise in einigen Feldern hat; ein Kreis kann eine Zahl beinhalten oder nicht. Die Aufgabe ist, einige Felder des Rastergitters entsprechend den folgenden Regeln zu schwärzen:

• Felder mit Kreisen dürfen nicht geschwärzt werden.
• Schwarze Felder bilden orthogonal zusammenhängende Flächen.
• Eine Zahl in einem Kreis gibt die Gesamtzahl der schwarzen Felder an, die sich in orthogonal benachbarten Bereichen des Feldes mit Kreis befinden.
• Felder mit leeren Kreisen können eine beliebige Anzahl von schwarzen Feldern um sich herum haben.

Tasukuea (aus dem Japanischen, wörtlich: "Quadrate finden") ist ein logisches Puzzle. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt mit Zahlen oder Fragezeichen in einigen Feldern. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Felder mit Zahlen oder Fragezeichen dürfen nicht geschwärzt werden.
• Schwarze Felder bilden quadratische Flächen, die nicht orthogonal zusammenhängen dürfen.
• Eine Zahl in einem Kreis gibt die Gesamtzahl der schwarzen Felder an, die sich in orthogonal benachbarten Bereichen des numerierten Feldes befinden.
• Ein Feld mit einem Fragezeichen muss wenigstens ein benachbartes schwarzes Feld haben.
• Alle weißen Felder müssen horizontal oder vertikal verbunden sein.

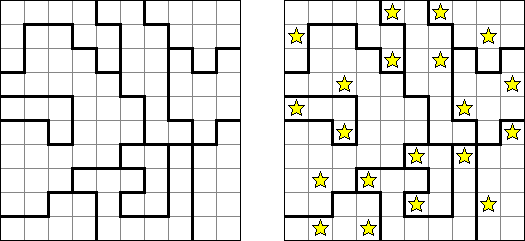
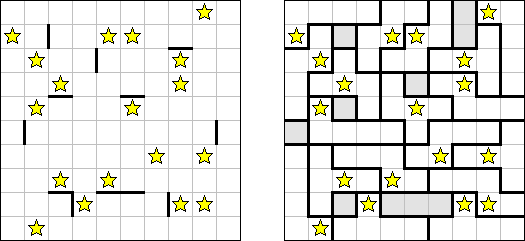
Sternenschlacht ("Star Battle") besteht aus einem quadratischen Rastergitter, das in Regionen aufgeteilt ist. Das Ziel ist, Sterne in einigen Feldern des Rastergitters so zu platzieren, dass jede Reihe, Spalte und Region die gleiche Anzahl von Sternen enthält. Sterne dürfen nicht in benachbarten Zellen und auch nicht diagonal platziert werden.

Araf (aus dem Türkischen, wörtlich: "Fegefeuer"; "Aidabeya") ist ein logisches Puzzle. Es wird auf einem rechteckigen Rastergitter gespielt. Einige Felder des Rastergitters sind nummeriert. Ziel ist es, das Rastergitter so in Bereiche zu unterteilen, dass jede Region genau zwei Zahlen enthält. Jede Region muss eine Fläche haben, deren Größe genau zwischen diesen beiden Zahlen liegt. Wenn beispielsweise die Region die Zahlen 2 und 5 enthält, dann muss die Fläche der Region 3 oder 4 sein.

Kabingurodo ("Curving Road", "Kurvige Straße") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Es besteht aus einem Rasteritter mit Kreisen in einigen Feldern. Ziel ist es, einige Felder des Rastergitters nach den folgenden Regeln zu schwärzen:

• Felder mit Kreisen sind immer weiß.
• Schwarze Felder dürfen nicht orthogonal verbunden sein.
• Alle weißen Felder müssen eine orthogonal zusammenhängende Fläche bilden.
• Jeder Weg von einem Kreis zu einem anderen Kreis in weißen Feldern muss mindestens zweimal abbiegen.

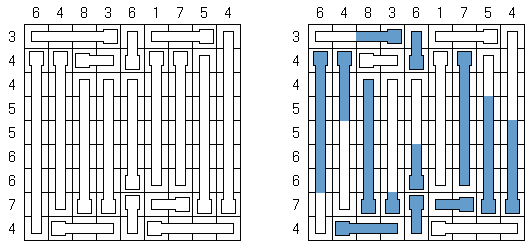
Thermometer ist ein logisches Puzzle. Das Rastergitter ist mit Thermometern ausgefüllt, die entweder nicht gefüllt, teilweise gefüllt oder vollständig gefüllt sind. Die Zahlen an der Außenseite geben an, wie viele Teile der Thermometer in dieser Reihe oder Spalte gefüllt sind. Jedes Thermometer wird von der Basis (Kreisteil) aus nach oben gefüllt. Dies hängt nicht von der tatsächlichen Ausrichtung des Thermometers ab.

Schlange ("Snake", "Tunnel") ist ein Logik-Puzzle. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt, in dem zwei Felder markiert sind. Die Aufgabe ist, eine einzelne Linie ("Schlange") zwischen den markierten Feldern einzuzeichnen; diese Linie darf sich nie selbst berühren, auch nicht diagonal. Zahlen am Rand des Rastergitters zeigen an, wie viele Felder in der entsprechenden Reihe oder Spalte geschwärzt sein müssen.

Peintoeria ("Paint Area", "Fläche anmalen") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Das Puzzle besteht aus einem rechteckigen Rastergitter von beliebiger Größe und ist in Gebiete aufgeteilt. Das Ziel ist, einige Felder des Rastergitters gemäß den folgenden Regeln zu schwärzen:

• Alle Felder eines Gebietes müssen die gleiche Farbe haben.
• Ein Feld mit einer Zahl gibt an, wie viele schwarze Felder benachbart sind.
• Alle schwarzen Felder müssen eine orthogonal zusammenhängende Fläche bilden.
• Kein Bereich von 2 x 2 Feldern innerhalb des Rastergitters kann die gleiche Farbe haben.

Irupu ("I-Loop", "I-Rundweg") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Kreise. Das Ziel ist, einige Blöcke in dem Rastergitter mit der Größe entweder 1 x 3 oder 3 x 1 zu lokalisieren. Jeder Block enthält einen Kreis und muss an genau zwei andere Blöcke orthogonal angrenzend sein. Alle Block-Felder bilden einen zusammenhängenden Bereich.

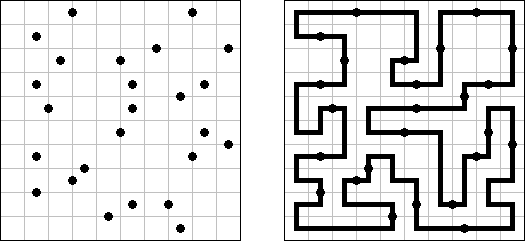
Sashigane (aus dem Japanischen, wörtlich: "Zimmermanns-Quadrat") ist ein logisches Puzzle, das von Nikoli veröffentlicht wurde. Das Ziel ist, das Rastergitter in L-förmige Bereiche aufzuteilen. Die beiden "Beine" eines Bereichs müssen genau ein Feld breit sein. Ein Kreis bezeichnet ein Feld, in welchem ein "L" eine Biegung hat (das Rastergitter enthält nicht für alle Bereiche Kreise). Ein Bereich muss die gleiche Anzahl von Feldern haben wie die Zahl im Kreis. Ein Pfeil markiert das Ende des "Beins" eines Bereichs; der Pfeil zeigt in Richtung des Feldes, in welchem sich das "L" biegt.

Sashikazune ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, das Rastergitter in L-förmige Gebiete zu unterteilen. Die beiden "Schenkel" eines Gebietes müssen genau ein Feld breit sein. Jedes Gebiet enthält nicht mehr als drei Felder mit Zahlen. Das Rastergitter kann Gebiete ohne Zahlen enthalten. Eine Zahl gibt die Anzahl der Felder bis zu einer Stelle an, an der sich ein "L" biegen muss (einschließlich dem Feld mit der Zahl). Ein Feld mit 1 stellt immer ein Feld dar, in dem sich ein "L" biegen muss.

Chocona ("Schokolade") besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete aufgeteilt ist. Das Ziel ist, einige Felder des Rastergitters nach den folgenden Regeln zu schwärzen:

• Ein Feld mit einer Zahl gibt an, wie viele Felder in dem Gebiet geschwärzt werden müssen.
• In einem Gebiet ohne Zahl kann eine beliebige Anzahl von Feldern geschwärzt sein.
• Die schwarzen Felder müssen Rechtecke bilden, unabhängig von den Grenzen des Gebiets.
• Die schwarzen Rechtecke dürfen nicht orthogonal benachbart sein.

Verschiedene Nachbarn ("Different Neighbours") besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete aufgeteilt ist. Ziel ist es, eine Zahl von 1 bis 4 in jedem Gebiet so zu platzieren, dass keine zwei Gebiete, die sich berühren (auch diagonal) die gleiche Zahl gemeinsam haben.

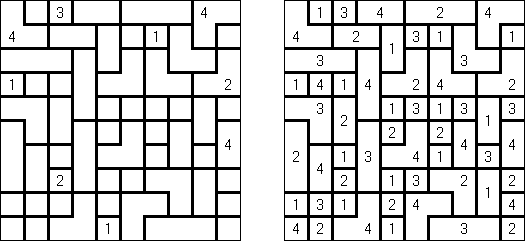
LITS ("Nuruomino") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Das Puzzle besteht aus einem rechteckigen Rastergitter von beliebiger Größe, welches in Gebiete aufgeteilt ist. Das Ziel ist, genau vier verbundene Felder in jedem Gebiet zu schwärzen, um ein L-, I-, T-, oder S-Tetromino zu bilden.

Die Tetrominos können gedreht oder gespiegelt werden. Wenn zwei Tetrominos in benachbarten Gebieten eine gemeinsame Kante haben, dürfen sie nicht von der gleichen Art sein. Alle Tetrominos müssen eine orthogonal zusammenhängende Fläche bilden. Die Tetrominos dürfen keine Fläche von 2 x 2 Feldern bedecken.

Nanbaboru ("Number Ball", "Zahlenball") besteht aus einem quadratischen Rastergitter. Ziel ist es, einige Felder mit Zahlen aus dem angegebenen Bereich zu füllen. Keine Zahl darf zweimal pro Zeile oder Spalte vorkommen. Ein Feld mit einem Kreis muss eine Zahl enthalten; ein Feld mit einem Kreuz darf keine Zahl enthalten.

Tairupeinto ("Tile Paint", "Crazy Pavement", "Verrückte Pflasterung") besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Regionen unterteilt ist. Das Ziel ist, einige Felder zu schwärzen, so dass jeder Bereich entweder vollständig gefüllt oder vollständig leer ist. Externe Zahlen sind die Hinweise für die jeweilige Gesamtsumme der schwarzen Quadrate in jeder Zeile und Spalte.

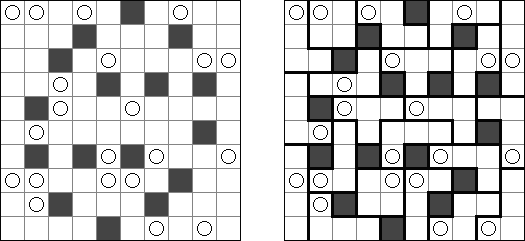
Yin-Yang besteht aus einem rechteckigen oder quadratischen Rastergitter mit weißen und schwarzen Kreisen in einigen Feldern. Ziel ist es, in jedes leere Feld einen schwarzen oder weißen Kreis so zu platzieren, dass alle Kreise der gleichen Farbe vertikal oder horizontal miteinander verbunden sind. Zusätzlich darf keine Gruppe von 2 x 2 Feldern Kreise der gleichen Farbe enthalten.

Nanro ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Die Aufgabe besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete aufgeteilt ist. Das Ziel ist, einige Felder mit Zahlen zu füllen. Alle Zahlen in einem Gebiet müssen gleich sein. Die gegebene Zahl in einem Gebiet zeigt, wie viele Felder in diesem Gebiet eine Zahl enthalten (alle Gebiete müssen mindestens eine Zahl haben). Wenn zwei Zahlen über eine Gebietsgrenze orthogonal benachbart sind, müssen sie unterschiedlich sein. Nummerierte Felder dürfen keine Fläche der Größe 2 x 2 oder größer bedecken. Alle Felder mit Zahlen müssen einen einzigen orthogonal zusammenhängenden Bereich bilden.

Licht und Schatten ("Light and Shadow") ist ein logisches Puzzle. Ziel ist, das Rastergitter in graue und weiße Bereiche aufzuteilen. Jeder Bereich enthält genau eine Zahl. Ein Bereich muss die gleiche Anzahl von Feldern haben wie die enthaltene Zahl. Zahlen in weißen Feldern sind Teil weißer Bereiche; Zahlen in grauen Feldern sind Teil von grauen Bereichen. Bereiche mit gleicher Farbe dürfen keine gemeinsame Kante haben.

Arukone ("Number Link", "Zahlenpaare") besteht aus einem rechteckigen oder quadratischen Rastergitter mit Zahlen in einigen Zellen. Ziel ist es, jedes Zahlenpaar mit einer einzigen fortlaufenden Linie zu verbinden. Die Linien dürfen sich weder kreuzen noch berühren.

Tetroid ist ein Logik-Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze Felder. Das Ziel ist, das Rastergitter in Bereiche von genau vier Feldern aufzuteilen, um ein L-, I-, T-, S- oder O- Tetromino zu formen.

Schwarze Felder gehören zu keinem Tetromino. Die Tetrominos können gedreht oder gespiegelt sein. Wenn zwei Tetrominos in benachbarten Bereichen eine gemeinsame Kante haben, dürfen sie nicht von der gleichen Art sein.

Sukima (nach dem japanischen "Sukimaburokku"; wörtlich: "Raum zwischen Blöcken") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erschaffen wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise in einigen Feldern. Ziel ist es, das Rastergitter in Regionen von genau drei Feldern aufzuteilen. Jede Region enthält einen Kreis. Jede 2 x 2 Region muss mindestens ein Feld enthalten, das zu keiner Region gehört. Schwarze Felder gehören zu keiner Region.

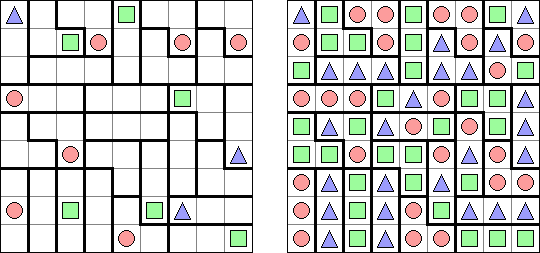
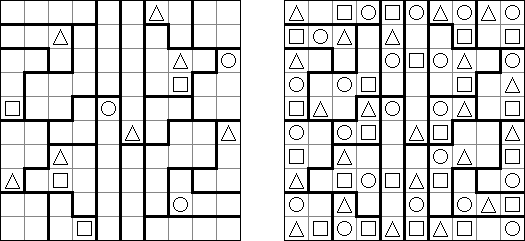
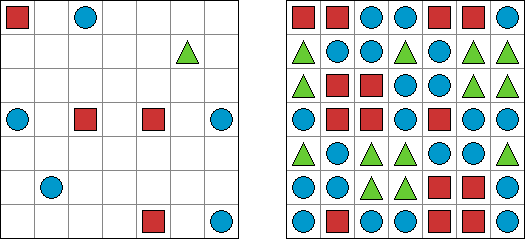
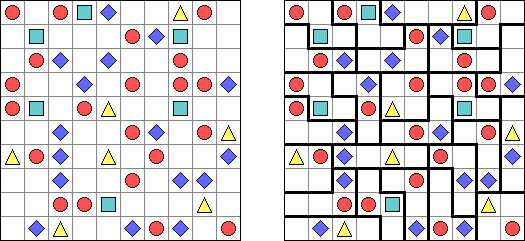
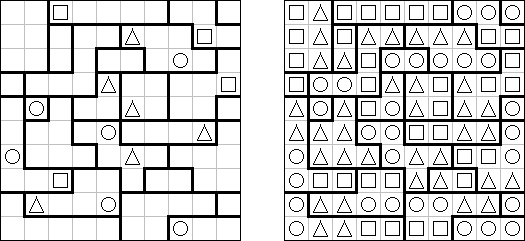
Tripletts ("Eines oder alle") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Das Puzzle besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete von genau drei Feldern aufgeteilt ist. Einige Felder enthalten Symbole von 3 verschiedenen Arten: Quadrate, Kreise, Dreiecke. Das Ziel ist, jedes Feld mit einer der drei Symbole zu füllen. In jedem Gebiet müssen alle Symbole gleich oder alle verschieden sein. Wenn zwei Symbole an einer Gebietsgrenze orthogonal benachbart sind, müssen die beiden Symbole verschieden sein.

Korekutokonekuto ("Correct Connection", "Korrekte Verbindung") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Die Aufgabe besteht aus weißen und schwarzen Kreisen; einige weiße Kreise können Zahlen enthalten. Das Ziel ist, alle weißen Kreise durch horizontale und vertikale Linien zu verbinden. Dabei dürfen die Linien andere Linien oder schwarze Kreise nicht kreuzen. Die Anzahl der Linien, die mit einem weißen Kreis verbunden sind, muss der Zahl in diesem Kreis entsprechen.

Doppelblock besteht aus einem quadratischen Rastergitter. Das Ziel ist, in jeder Reihe und jeder Spalte zwei Felder zu schwärzen. Die verbleibenden weißen Felder müssen mit den Zahlen von 1 bis N-2 ausgefüllt werden, wobei N die Größe der Puzzle-Seite ist. Jede Zahl erscheint einmal in jeder Reihe und Spalte. Zahlen am Rand zeigen die Summen der Zahlen zwischen zwei schwarzen Feldern in der entsprechenden Reihe oder Spalte an.

Furisuri ("Free Three") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise in einigen Feldern. Das Ziel ist, einige Blöcke mit der Größe von genau drei Feldern in dem Rastergitter zu lokalisieren. Jeder Block muss einen Kreis enthalten. Es muss möglich sein, jeden Block ein Feld in wenigstens einer Richtung zu verschieben.

Yagit (aus dem Japanischen "Yagi to ookami"; wörtlich: "Ziege und Wolf") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Die Aufgabe besteht aus einem rechteckigen oder quadratischen Rastergitter mit Kreisen ("Ziegen") und Quadraten ("Wölfen") in einigen Feldern. Die Aufgabe besteht darin, das Gitter in Gebiete zu unterteilen. Jedes Gebiet muss entweder Ziegen oder Wölfe (aber nicht beide) enthalten und darf nicht leer sein. Die Grenzlinien der Gebiete beginnen und enden an den Rändern des Rastergitters. Linien dürfen nur an schwarzen Punkten abbiegen. Linien können einander kreuzen außer an schwarzen Punkten. Nicht alle schwarzen Punkte müssen von Grenzlinien verwendet werden.

Purenrupu ("Pure Loop", "Einfacher Rundweg") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze Felder. Das Ziel ist, einen einzigen Rundweg einzuzeichnen. Der Rundweg führt genau einmal durch jedes weiße Feld. Die Segmente des Rundwegs verlaufen horizontal und vertikal zwischen den Mittelpunkten der weißen Felder.

Firumatto ("Fillmat") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Es ist notwendig, das Rastergitter in Rechtecke zu zerlegen. Jedes Rechteck muss genau ein Feld breit sein; die andere Seite des Rechtecks hat die Länge von 1 bis 4 Feldern. Ein Feld mit einer Zahl gibt die Größe eines Rechtecks an. Zwei Rechtecke von gleicher Größe dürfen nicht orthogonal benachbart sein. Ein Rastergitterpunkt darf nicht zu vier Rechtecken gehören.

Nawabari ("Gebiet", "Territorium") ist ein logisches Puzzle, das von Nikoli veröffentlicht wurde. Ziel ist es, das Rastergitter in rechteckige Bereiche zu unterteilen, so dass jeder Bereich genau eine Zahl enthält. Die Zahl in dem Feld zeigt an, wie viele Seiten des Feldes zu den Grenzen der Bereiche gehören, einschließlich der Kante des Rastergitters.

Makaro ist ein von Nikoli veröffentlichtes Logik-Puzzle. Ein rechteckiges oder quadratisches Rastergitter ist in Bereiche unterteilt. Jeder Bereich muss mit jeder der Zahlen von 1 bis zur Anzahl der Felder in dem Bereich gefüllt werden. Das Rastergitter enthält schwarze Felder mit Pfeilen. Der Pfeil zeigt auf die größte Zahl der Zahlen in den bis zu vier Feldern (oben, unten, links, rechts) um das schwarze Feld herum. Wenn zwei orthogonal benachbarte Zahlen zu verschiedenen Bereichen gehören, müssen sie verschieden sein.

Dosun-Fuwari ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Die Aufgabe besteht aus einem Rastergitter, das in Bereiche aufgeteilt ist. Das Rastergitter enthält schwarze Felder; nicht zu jedem Bereich gehört ein schwarzes Feld. Das Ziel ist, in jedem Bereich einen schwarzen und einen weißen Kreis nach den folgenden Regeln zu platzieren:

• Weiße Kreise ("Ballons") sind leicht und schweben, so müssen sie entweder in das oberste Feld des Rastergitters oder in das Feld direkt unter dem schwarzen Feld oder unter einen anderen weißen Kreis platziert werden.
• Schwarze Kreise ("Eisenkugeln") sind schwer und sinken, so müssen sie entweder in das untere Feld des Rastergitters oder in das Feld direkt über dem schwarzen Feld oder über einem anderen schwarzen Kreis platziert werden.

Satogaeri (aus dem Japanischen, wörtlich: "nach Hause kommen") ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Einige Felder des Rastergitters enthalten Kreise (leer oder mit Zahlen). Aufgabe ist, die Kreise vertikal oder horizontal so zu bewegen, dass jedes Gebiet nur einen Kreis enthält. Die Zahlen in den Kreisen zeigen an, wie viele Felder sie zu durchlaufen haben. Kreise ohne Zahlen können beliebig weit bewegt werden, aber einige von ihnen können sitzen bleiben. Die Kreise dürfen die Bahnen von anderen Kreisen nicht überqueren und dürfen nicht über andere Kreise bewegt werden.

Koburin ist ein von Nikoli veröffentlichtes Logik-Puzzle. Eine rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Das Ziel ist, einige Felder zu schwärzen und einen einzigen kontinuierlichen, nicht-schneidenden Rundweg zu zeichnen, der genau durch alle leeren weißen Felder führt. Die Zahl in einem Feld gibt die Gesamtzahl der schwarzen Felder an, die orthogonal zu diesem Feld benachbart sind. Das Rastergitter kann schwarze Felder enthalten, die keine benachbarten Felder mit Zahlen haben. Felder mit Zahlen dürfen nicht geschwärzt werden. Zwei schwarze Felder dürfen nicht orthogonal benachbart sein.

Sukrokuro kombiniert die Elemente von drei Logik-Puzzles: Sudoku, Kropki Sudoku und Kakuro. Es besteht aus einem quadratischen Rastergitter mit weißen und schwarzen Feldern. Das Ziel ist, in jedes weiße Feld eine Zahl zu schreiben, so dass jede Spalte und Zeile die Zahlen von 1 bis N genau einmal enthält. Schwarze Felder enthalten einen Schrägstrich von oben links nach unten rechts mit Zahlen in ihnen, genannt "Hinweise". Eine solche Zahl gibt die Summe der Zahlen in aufeinanderfolgenden Feldern nach rechts oder nach unten an. Wenn die absolute Differenz zwischen zwei Zahlen in benachbarten Feldern gleich 1 ist, dann werden sie durch einen Punkt getrennt. Wenn es zwischen zwei weißen Feldern keinen Punkt gibt, ist die Differenz zwischen den Zahlen in diesen Feldern mehr als 1.

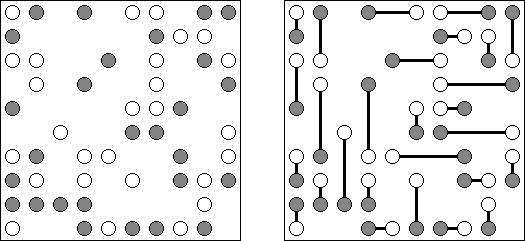
Shirokuro ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Es enthält weiße und schwarze Kreise. Die Aufgabe ist, jeden weißen Kreis mit einem schwarzen Kreis durch eine horizontale oder vertikale Linie zu verbinden. Linien dürfen andere Linien nicht kreuzen. Die Linie zwischen zwei Kreisen darf nicht durch andere Kreise gehen.

Roma (von der mittelalterlichen Ansicht "alle Wege führen nach Rom") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Einige Felder des Rastergitters enthalten schwarze Kreise. Ziel ist es, in jedes leere Feld einen Pfeil einzuzeichnen, der in eine von vier Richtungen zeigt. Jedes Gebiet muss alle verschiedenen Pfeile enthalten. Wenn man von einem beliebigen Feld ausgehend den Pfeilen von Feld zu Feld folgt, muss dieser Pfad in dem Feld mit dem schwarzen Kreis enden.

Bodaburokku ("Border Block") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Zahlen in einigen Feldern. Es ist notwendig, das Rastergitter in Gebiete zu unterteilen. Felder mit der gleichen Zahl gehören zu dem gleichen Gebiet. Alle Punkte, in denen sich drei oder vier Linien treffen, sind eingezeichnet. Jedes Gebiet enthält mindestens ein Feld mit einer Zahl.

Kuroshuto ("Kurochute", aus dem Japanischen, wörtlich "schwarzer Schuss") ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Zahlen in einigen Feldern. Ziel ist es, einige leere Felder zu schwärzen. Ein Feld mit einer Zahl zeigt an, dass nur eines der Felder mit einem derartigen Abstand geschwärzt werden muss. Zwei schwarze Felder dürfen nicht orthogonal benachbart sein. Alle der weißen Felder müssen miteinander verbunden sein.

Toichika ist ein Logik-Puzzle, das von Gesaku (Japan) erstellt wurde. Die Aufgabe besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Bereiche aufgeteilt ist. Das Ziel ist, Pfeile in einigen Feldern nach den folgenden Regeln zu platzieren:

• Jeder Bereich enthält genau einen Pfeil.
• Jeweils zwei Pfeile sind gepaart, sie weisen zueinander. Es gibt keine ungepaarten Pfeile.
• Zwischen zwei gepaarten Pfeilen muss mindestens ein Bereich sein, in dem keiner der zwei gepaarten Pfeile angeordnet ist.
• Zwischen zwei gepaarte Pfeile darf kein anderer Pfeil gesetzt werden.

Usotatami ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, das Rastergitter so in rechteckige Bereiche zu unterteilen, dass jeder Bereich genau eine Zahl enthält. Jeder Bereich muss genau ein Feld breit sein; die Länge der anderen Seite ist NICHT gleich der Zahl in diesem Bereich. In einem Rasterpunkt dürfen sich nicht die Ecken von vier Bereichen treffen.

Pipelink besteht aus einem rechteckigen oder quadratischen Rastergitter. Die Aufgabe besteht darin, einen einzigen durchgehenden Rundweg zu zeichnen, der alle Felder durchläuft. Der Rundweg muss alle angegebenen Abschnitte verwenden und kann sich in jedem Feld kreuzen.

Hakoiri ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter wird in Gebiete unterteilt. Das Ziel ist, in jedem Gebiet genau ein Dreieck, ein Quadrat und einen Kreis zu platzieren. Die gleichen Symbole dürfen nicht in benachbarten Feldern platziert werden, auch nicht diagonal. Alle Symbole müssen horizontal oder vertikal verbunden sein.

Nuribou ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Zahlen in einigen Feldern. Die Aufgabe besteht darin, leere Felder nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder teilen das Rastergitter in Bereiche weißer Felder. Jeder Bereich enthält ein Feld mit einer Zahl.
• Jeder Bereich muss die gleiche Anzahl an weißen Feldern wie die darin enthaltene Zahl enthalten (einschließlich des nummerierten Feldes).
• Schwarze Felder bilden horizontale oder vertikale Streifen, die nicht orthogonal benachbart sein dürfen. Jeder Streifen muss genau ein Feld breit sein.
• Sind zwei Streifen diagonal verbunden, muss die Länge der Streifen unterschiedlich sein.

Tatamibari ist ein Logikpuzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält 3 Arten von Symbolen: Kreuz, horizontaler Balken, vertikaler Balken. Ziel ist es, das Rastergitter in rechteckige Bereiche zu unterteilen. Jeder Bereich enthält ein Feld mit einem Symbol. Ein Bereich mit einem Kreuz muss ein Quadrat sein. Wenn ein Bereich einen horizontalen Balken enthält, muss die Breite des Bereichs größer sein als seine Höhe. Wenn ein Bereich einen vertikalen Balken enthält, muss die Breite des Bereichs kleiner als seine Höhe sein. Ein Rasterpunkt darf nicht von den Ecken von vier Bereichen geteilt werden.

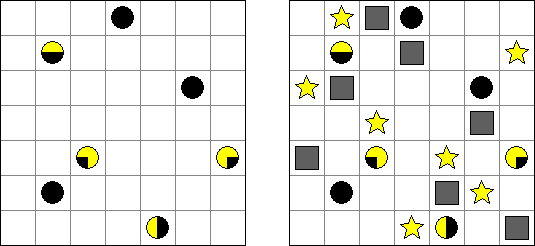
Sternenhaufen ("Sun and Moon", "Sonne und Mond", "Munraito") ist ein Logikpuzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein quadratisches Rastergitter enthält in einigen Feldern Planeten. Das Ziel ist, genau einen Stern und eine Sternenstaubwolke in jede Reihe und jede Spalte des Rastergitters zu setzen. Wenn ein bestimmter Halbkreis eines Planeten beleuchtet wird, muss es einen Stern in diesem Rang geben, um ihn zu beleuchten. Ein Stern leuchtet nur horizontal und vertikal; Planeten und Sternenstaubwolken blockieren Sternlicht.

Kojun ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Einige Felder enthalten Zahlen. Jedes Gebiet muss mit jeder der Zahlen von 1 bis zur Anzahl der Felder in dem Gebiet gefüllt werden. Wenn zwei Zahlen orthogonal benachbart sind, müssen die Zahlen unterschiedlich sein. Die obere Zahl von zwei vertikal benachbarten Zahlen im gleichen Gebiet muss größer sein als die untere Zahl.

Usowan (aus dem Japanischen, wörtlich "ein Lügner") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein Rastergitter ist in rechteckige und quadratische Regionen unterteilt. Einige der Felder im Rastergitter sind nummeriert. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Felder mit Zahlen sind immer weiß.
• Eine Zahl in einem Feld zeigt an, wie viele schwarze Felder angrenzend an ihre vier Seiten platziert werden müssen. Jedoch gibt es in jeder Region eine (und nur eine) falsche Zahl (sie zeigt eine falsche Menge an schwarzen Feldern).
• Zwei schwarze Felder dürfen nicht orthogonal benachbart sein.
• Alle weißen Felder müssen verbunden sein.

Gokigen Naname (aus dem Japanischen, wörtlich "in schlechter Laune", auch bekannt als "Slalom", "Slant") ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Kreise mit Zahlen von 0 bis 4 können auf Kreuzungen von Linien innerhalb des Rastergitters liegen. Ziel ist es, in jedes Feld eine diagonale Linie einzuzeichnen. Die Zahl in jedem Kreis entspricht der Anzahl der Linien, die sich von diesem Kreis erstrecken. Die diagonalen Linien dürfen keine geschlossene Schleife bilden.

Hebi-Ichigo ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ziel ist es, die Zahlen 1 bis 5 nach den folgenden Regeln einzufügen:

• Zahlen bilden eine Kette von fünf aufeinanderfolgenden Feldern von 1 ("Kopf") bis 5 ("Schwanz"), die horizontal und vertikal verbunden sind ("Schlange").
• Schlangen dürfen andere Schlangen horizontal oder vertikal nicht berühren, diagonal ist erlaubt.
• Schlangen dürfen nicht vor dem Kopf einer anderen Schlange erscheinen. Die Augen der Schlange befinden sich auf einer Seite des Kopfes (Feld mit der Nummer 1), gegenüber der Seite, mit welcher der Körper (Feld mit Nummer 2) verbunden ist. Eine Schlange schaut in die Richtung ihrer Augen, bis ein schwarzes Feld oder der Rand des Rastergitters erreicht ist.
• Die Zahl im schwarzen Feld zeigt den Wert der nächsten Zahl in Pfeilrichtung an. Diese Zahl muss vor jedem anderen schwarzen Feld erscheinen. Ein schwarzes Feld mit einer Null bedeutet, dass es keine Schlange in Richtung des Pfeils bis zum nächsten schwarzen Feld oder zum Rand des Rastergitters gibt.

Hamle (aus dem Türkischen, wörtlich "bewegen") besteht aus einem rechteckigen oder quadratischen Rastergitter. Ziel ist es, jedes nummerierte schwarze Feld in einer der vier Richtungen zu bewegen, so dass die Zahlen in den Feldern die Länge ihrer Bewegungen angeben. Wenn alle Bewegungen durchgeführt wurden, sollten alle weißen Felder miteinander verbunden sein, aber nummerierte Felder sollten keine Kante gemeinsam haben.

Gyokuseki (aus dem Japanischen, wörtlich "Edelsteine ​​und Steine") ist ein Logik-Puzzle von Naoki Inaba (Japan). Das Ziel ist, ein quadratisches Rastergitter mit schwarzen Kreisen ("Edelsteinen") und weißen Kreisen ("Steinen") zu füllen. Jede Zeile und jede Spalte enthält einen schwarzen Kreis und eine willkürliche Anzahl von weißen Kreisen. Eine Zahl am Rand des Puzzles zeigt an, wie viele Kreise in der entsprechenden Zeile oder Spalte bis zum schwarzen Kreis zu sehen sind.

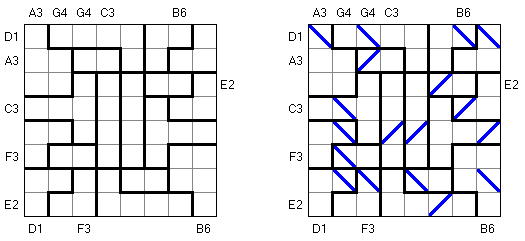
Kin-Kon-Kan ist ein Logik-Puzzle von Nikoli. Die Aufgabe besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Bereiche unterteilt ist. Das Ziel ist, einige Felder mit diagonalen Linien ("Spiegeln") zu füllen. Jeder Bereich enthält genau einen Spiegel. Buchstaben-Zahlenpaare an den Rändern des Rastergitters können durch gerade Linien ("Laserstrahlen") verbunden werden, die an der gleichen Anzahl von Spiegeln abprallen wie die Zahl im Buchstaben-Zahlenpaar. Jeder Spiegel muss mindestens einen Laserstrahl reflektieren.

Ichimaga ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Die Aufgabe besteht darin, alle Kreise durch horizontale und vertikale Linien zu verbinden. Die Anzahl der mit dem Kreis verbundenen Linien muss mit der Zahl in diesem Kreis übereinstimmen. Eine beliebige Anzahl von Linien kann mit dem leeren Kreis (mindestens jedoch eine) verbunden sein. Die Linien dürfen keine anderen Linien überqueren. Eine Linie darf nicht mehr als einmal ihre Richtung um 90 Grad ändern.

Shimaguni ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Regionen unterteilt. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Alle schwarzen Felder in einer Region müssen verbunden sein.
• Ein Feld mit einer Zahl gibt an, wie viele Felder in der Region geschwärzt werden müssen.
• In Regionen ohne Zahl kann jede beliebige Anzahl von Feldern geschwärzt werden (mindestens eins).
• Zwei Regionen mit der gleichen Anzahl an schwarzen Feldern dürfen nicht orthogonal benachbart sein.
• Wenn zwei Felder an einer Regionengrenze orthogonal benachbart sind, muss mindestens ein Feld weiß sein.

Kuhweide ("Meadows") ist ein Logik-Puzzle. Es wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Einige der Felder haben Kreise. Ziel ist es, das Rastergitter in quadratische Blöcke aufzuteilen, so dass jeder Block genau einen Kreis enthält.

Yajisan-Kazusan (aus dem Japanischen, wörtlich "Pfeil-Nummer") ist ein Logik-Puzzle, das von Nikoli veröffentlicht wurde. Ziel ist es, einige Felder nach folgenden Regeln zu schwärzen:

• Schwarze Felder dürfen nicht orthogonal verbunden sein.
• Ein Feld mit einer Zahl kann geschwärzt werden.
• Alle weißen Felder müssen einen orthogonal zusammenhängenden Bereich bilden.
• Ein Feld, das eine Zahl und einen Pfeil enthält, zeigt, wie viele schwarze Felder in der Zeile oder Spalte sind, auf die der Pfeil zeigt.
• Nummerierte Felder müssen geschwärzt werden, wenn sie falsche Hinweise enthalten, aber nummerierte Felder, die geschwärzt sind, enthalten nicht unbedingt falsche Hinweise.

Schlangengrube ("Snake Pit") besteht aus einem rechteckigen oder quadratischen Rastergitter. Das Ziel ist, das Rastergitter nach den folgenden Regeln in Regionen ("Schlangen") aufzuteilen:

• Eine Schlange ist ein Weg mit der Breite eines Feldes, der mindestens zwei Felder lang ist. Eine Schlange darf sich selbst nicht berühren, nicht einmal diagonal.
• Ein Feld mit einem Kreis muss sich an einem der Enden einer Schlange befinden. Eine Schlange kann ein Feld mit einem Kreis, zwei Felder mit einem Kreis oder gar kein Feld mit einem Kreis enthalten.
• Ein Feld mit einer Zahl muss Teil einer Schlange mit einer Länge von genau dieser Anzahl von Feldern sein. Eine Schlange kann jede beliebige Menge nummerierter Felder enthalten.
• Zwei Schlangen gleicher Länge dürfen nicht orthogonal benachbart sein.
• Ein Feld mit einem Kreuz darf kein Ende einer Schlange sein.

Hiroimono ("Goishi Hiroi", aus dem Japanischen, wörtlich "Eingesammelte Dinge") ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Das Rastergitter enthält Kreise ("Steine"), die an einigen Rasterpunkten platziert sind. Die Aufgabe besteht darin, sich entlang der Gitterlinien zu bewegen und dabei alle Steine einzusammeln (nummeriere sie in der Reihenfolge, in der du sie aufsammelst) nach folgenden Regeln:

• Beginne bei jedem beliebigen Stein.
• Wenn ein Stein angetroffen wird, wird er eingesammelt.
• Wenn ein Stein eingesammelt wurde, kann die Richtung geändert werden.
• Es ist nicht erlaubt, die Richtung umzukehren.

Wasserspaß ("Water Fun", "Wasserspielerei", "Aquarium") wird auf einem rechteckigen oder quadratischen Rastergitter gespielt. Das Ziel ist, Wasser in einige Gebiete des Rastergitters zu füllen. Zahlen außerhalb des Rastergitters zeigen an, wie viele Felder jeder Zeile und Spalte mit Wasser gefüllt werden müssen. Verbundene Gebiete mit gefüllten Feldern müssen überall den gleichen Wasserstand haben wie in einer Folge von verbundenen Röhren.

Rundreise ("Round Trip") ist eine Art Logikrätsel. Ziel ist es, einen Rundweg in einem rechteckigen oder quadratischen Rastergitter einzuzeichnen. Ein Rundweg kann sich selbst orthogonal kreuzen, berührt sich aber ansonsten selbst nicht. Die Zahlen am Rand des Puzzles zeigen die Anzahl der Felder an, die vom nächsten Abschnitt des Rundwegs in der entsprechenden Zeile oder Spalte besucht werden.

Zahlenkreuz ("Number Cross") besteht aus einem quadratischen Rastergitter mit Zahlen. Das Ziel ist, einige Felder zu schwärzen. Zahlen außerhalb des Rastergitters zeigen die Summen der Zahlen in den weißen Feldern in der entsprechenden Zeile oder Spalte an.

Santoitchi (aus dem Japanischen "San to itchi"; wörtlich: "drei und eins") ist ein Logikrätsel, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Die Aufgabe besteht darin, einige leere Felder gemäß den Regeln zu schwärzen:

• Alle weißen Felder müssen in Regionen mit der Größe von genau drei Feldern aufgeteilt werden.
• Zwei schwarze Felder dürfen nicht orthogonal benachbart sein.
• Jede Region enthält eine Zahl.
• Eine Zahl gibt an, wie viele schwarze Felder eine Kante mit dieser Region teilen.

Hamusando ("Ham Sandwich", "Schinkensandwich") ist ein Logikrätsel, das von Naoki Inaba (Japan) erfunden wurde. Das Ziel besteht darin, ein quadratisches Rastergitter mit Quadraten (Sandwiches) und Kreisen (Schinkenstücken) zu füllen. Jede Reihe und jede Spalte enthält zwei Quadrate und N Kreise (N ist für jedes Puzzle angegeben). Eine Zahl am Rand des Rasters gibt an, wie viele Kreise zwischen den zwei Quadraten in der entsprechenden Zeile oder Spalte platziert werden müssen.

Pfadfinder ("Trace Numbers") besteht aus einem rechteckigen oder quadratischen Rastergitter mit Zahlen in einigen Feldern. Das Ziel ist, so viele Pfade in das Rastergitter zu zeichnen, wie es Felder mit der Zahl 1 gibt. Ein Pfad darf nur horizontal oder vertikal und niemals diagonal verlaufen. Ein Pfad beginnt in dem Feld mit der Zahl 1 und besucht alle Felder mit Zahlen in der Reihenfolge bis zur höchsten Zahl. Jedes Feld muss genau einmal besucht werden; Pfade dürfen sich nicht kreuzen.

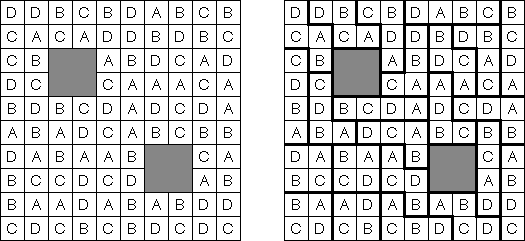
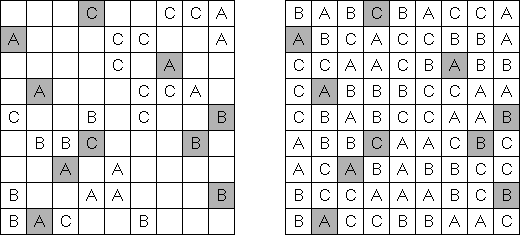
Area Division wird auf einem Rastergitter mit lateinischen Buchstaben gespielt. Ziel ist es, das Raster in Regionen zu unterteilen. Jede Region enthält alle Buchstaben des angegebenen Bereichs. Eine Region enthält jeden Buchstaben genau einmal. Jeder Buchstabe muss zu genau einer Region gehören.

Sukoro besteht aus einem rechteckigen oder quadratischen Rastergitter mit Zahlen von 1 bis 4 in einigen Feldern. Die Zahl innerhalb eines Feldes gibt an, wie viele benachbarte Felder Zahlen enthalten. Wenn zwei Felder mit Zahlen orthogonal benachbart sind, müssen die Zahlen unterschiedlich sein. Alle Felder mit Zahlen müssen horizontal oder vertikal verbunden sein.

EntryExit besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Bereiche unterteilt ist. Ziel ist es, eine einzige durchgehende, sich nicht kreuzende Schleife zu zeichnen, die alle Felder durchläuft. Sie darf jeden Bereich nur einmal betreten und verlassen.

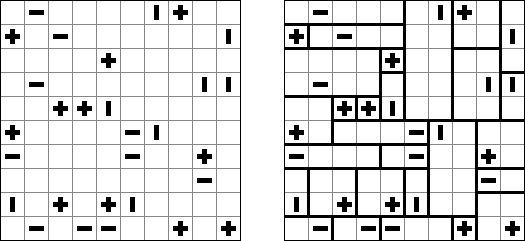
Sign In wird auf einem quadratischen Rastergitter gespielt. Das Ziel ist, jedes Feld mit Zahlen von 1 bis N zu füllen, wobei N die Anzahl der Felder einer Puzzle-Seite ist. In keiner Zeile oder Spalte darf eine Zahl zweimal vorkommen. Einige Zahlen können am Anfang vorgegeben sein. Wenn die absolute Differenz zwischen zwei Zahlen in benachbarten Feldern gleich 1 ist, werden sie durch ein Zeichen "+" oder "-" getrennt. Wenn eine Grenze zwischen Feldern das Zeichen "+" enthält, ist eine Zahl im linken oder oberen Feld um eine Zahl niedriger als eine Zahl in einem rechten oder unteren Feld. Wenn eine Grenze zwischen Feldern das Zeichen "-" enthält, ist eine Zahl in einem linken oder oberen Feld größer als eine Zahl in einem rechten oder unteren Feld. Alle Fälle von aufeinanderfolgenden Zahlen werden durch diese Zeichen angezeigt.

Kuroshiro ("Kuroshirorupu"; aus dem Japanischen, wörtlich "Schwarz-Weiß-Rundweg") wird auf einem Rastergitter mit schwarzen und weißen Kreisen in einigen Feldern gespielt. Das Ziel besteht darin, einen einzelnen kontinuierlichen, sich nicht überschneidenden Rundweg zu zeichnen, der alle Felder mit Kreisen ordnungsgemäß durchläuft. Zwischen zwei aufeinanderfolgenden Kreisen gleicher Farbe darf der Rundweg nicht abbiegen. Zwischen zwei aufeinanderfolgenden Kreisen unterschiedlicher Farben muss der Rundweg genau einmal abbiegen.

Moonsun ("Moon or Sun", "Mond oder Sonne") ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Das Rastergitter enthält in einigen Feldern schwarze und weiße Kreise. Ziel ist es, einen einzigen sich nicht überschneidenden Rundweg zu zeichnen. Der Rundweg muss die Grenzen von jedem Gebiet genau zweimal überschreiten. In einem Gebiet muss der Rundweg entweder alle Felder mit schwarzen Kreisen oder alle Felder mit weißen Kreisen besuchen. Gebiete mit besuchten schwarzen Kreisen müssen sich mit Gebieten abwechseln, in denen weiße Kreise besucht wurden.

Rectslider ("Rectangle-Slider", "Shikaku suraida") besteht aus einem rechteckigen oder quadratischen Rastergitter mit schwarzen Feldern. Die Aufgabe besteht darin, die schwarzen Felder vertikal oder horizontal zu bewegen, so dass schwarze Felder Rechtecke mit einer Fläche größer als ein Feld bilden. Zwei schwarze Rechtecke dürfen nicht orthogonal nebeneinander liegen. Die Zahlen in den schwarzen Feldern geben an, wie viele Felder sie passieren müssen. Schwarze Felder ohne Zahlen können sich beliebig weit bewegen, aber einige bleiben stehen. Die schwarzen Felder dürfen die Spuren anderer schwarzer Felder nicht kreuzen und dürfen sich nicht über andere schwarze Felder bewegen.

Stostone ("Sto-Stone", "Stone on Stone", "Stein auf Stein") ist ein von Nikoli erfundenes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter ist in Regionen unterteilt. Das Ziel ist, einige Felder eines Rastergitters ("Steine") nach folgenden Regeln zu schwärzen:

• Alle schwarzen Felder in einer Region müssen horizontal oder vertikal verbunden sein.
• Ein Feld mit einer Zahl gibt an, wie viele Felder in der Region geschwärzt werden müssen.
• In Regionen ohne eine Zahl kann jede beliebige Anzahl von Feldern geschwärzt sein (mindestens eins).
• Wenn zwei Felder über eine Bereichsgrenze orthogonal benachbart sind, muss mindestens ein Feld weiß sein.
• Wenn alle Steine ​​"runterfallen", müssen sie genau die untere Hälfte des Rastergitters abdecken.

Milchkaffee ("Kohi Gyunyu"; aus dem Japanischen) besteht aus weißen, schwarzen und grauen Kreisen. Ziel ist es, Kreise durch horizontale und vertikale Linien zu verbinden. Alle verbundenen Kreise bilden eine Gruppe. Jede Gruppe muss genau einen grauen Kreis und die gleiche Anzahl weißer und schwarzer Kreise enthalten. Linien dürfen keine anderen Linien kreuzen. Weiße und schwarze Kreise dürfen nicht direkt verbunden werden.

Milchtee ("Mirukuti"; aus dem Japanischen, wörtlich "Milch-Tee"; auch bekannt als "Milk-T") besteht aus einem rechteckigen oder quadratischen Rastergitter mit schwarzen und weißen Kreisen in einigen Feldern. Das Ziel besteht darin, jede Gruppe von drei Kreisen (ein schwarzer Kreis und zwei weiße Kreise) durch eine T-förmige Linie zu verbinden. Zwei weiße Kreise müssen durch das geradlinige Segment der T-förmigen Linie verbunden sein. Die Linien dürfen keine anderen Linien kreuzen.

Slash Pack ist ein Logik-Puzzle, das von Yosuke Imai (Japan) erfunden wurde. Das Rastergitter mit unregelmäßiger Form enthält in einigen Feldern Zahlen von 1 bis N. Die Aufgabe besteht darin, das Rastergitter in Regionen zu unterteilen, indem diagonale Linien in leere Zellen platziert werden. Jede Region muss die Zahlen von 1 bis N genau einmal enthalten. Zwei Diagonalen dürfen sich nicht in einem Feld kreuzen, und es darf keine losen Enden geben.

Nurimaze ("Nurimeizu"; aus dem Japanischen, wörtlich "Farblabyrinth") besteht aus einem Rastergitter, das in Gebiete aufgeteilt ist. Ziel ist es, einige Gebiete nach folgenden Regeln zu schwärzen:

• Felder mit Buchstaben, Kreisen oder Dreiecken sind immer weiß.
• Weiße Felder bilden einen Pfad von einem Feld mit S (Start) zu einem Feld mit G (Goal, Ziel). Der Pfad muss genau ein Feld breit sein.
• Der Pfad von S nach G enthält alle Felder mit Kreisen und keine Felder mit Dreiecken.
• Kein Bereich der Größe von 2 x 2 Feldern innerhalb des Rastergitters kann die gleiche Farbe haben.
• Alle weißen Felder müssen eine orthogonal zusammenhängende Fläche bilden.
• Weiße Felder dürfen keinen Rundweg bilden.

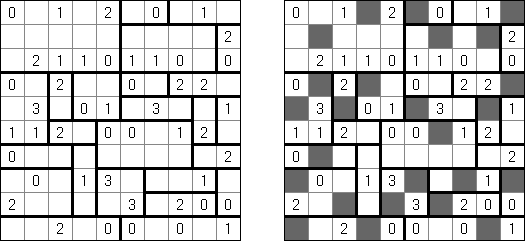
Kanalansicht ("Canal View") wird auf einem rechteckigen Rastergitter gespielt. Einige der Felder enthalten Zahlen. Ziel ist es, einige Felder eines Rastergitters nach folgenden Regeln zu schwärzen:

• Alle schwarzen Felder erstellen eine einzige verbundene Gruppe.
• Kein Bereich von 2 x 2 Feldern innerhalb des Rastergitters darf aus ausschließlich schwarzen Feldern bestehen.
• Nummerierte Felder dürfen nicht schwarz sein.
• Jedes nummerierte Feld gibt die Gesamtzahl der schwarzen Felder an, die vertikal und horizontal mit dem nummerierten Feld verbunden sind, in einer geraden Linie bis zum nächsten weißen Feld oder der Kante des Rastergitters.

Country Road ist ein Logik-Puzzle, das von Nikoli erfunden wurde. Das Puzzle besteht aus einem rechteckigen Rastergitter beliebiger Größe, das in Bereiche unterteilt ist. Das Ziel besteht darin, einen einzigen durchgehenden, sich nicht überschneidenden Rundweg zu zeichnen, der die Mittelpunkte der Felder verbindet. Der Rundweg muss jeden Bereich genau einmal besuchen. Die Zahl in einem Bereich gibt an, wie viele Felder dieses Bereichs von dem Rundweg besucht werden. In Bereichen ohne Zahl kann der Rundweg eine beliebige Anzahl von Feldern besuchen. Wenn der Rundweg zwei benachbarte Felder nicht besucht, müssen sich diese Felder in demselben Bereich befinden.

Nondango (Dango ist ein japanisches Gericht: kleine Reismehl-Bällchen aufgespießt auf Bambusstäbchen) ist ein Logikrätsel, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Bereiche unterteilt. Jeder Bereich enthält in einigen Feldern Kreise. Ziel ist es, einige Kreise nach folgenden Regeln zu schwärzen:

• Jeder Bereich enthält einen schwarzen Kreis.
• Drei aufeinanderfolgende Kreise gleicher Farbe erscheinen nie in einer Zeile, Spalte oder Diagonale. Zwischen ihnen muss ein Kreis mit anderer Farbe oder ein leeres Feld sein.

Mintonette (der ursprüngliche Name des Spiels wurde bekannt als Volleyball) wird auf einem Rastergitter von irregulärer Form mit Kreisen in einigen Feldern gespielt. Das Ziel besteht darin, Kreise paarweise zu verbinden, indem eine Linie gezogen wird, die horizontal und vertikal durch die Feldermitten verläuft. Linien dürfen sich weder berühren noch kreuzen. Wenn ein Kreis eine Zahl enthält, stellt diese die Anzahl der Abbiegungen der Linie zwischen zwei Kreisen dar. Wenn zwei Kreise keine Zahl haben, kann eine Linie beliebig viele Abbiegungen zwischen den Kreisen machen. Alle Felder müssen von den Linien verwendet werden und jeder Kreis muss mit einem anderen Kreis verbunden sein.

Pfeilpfad ("Arrow Maze", "Arrow Path") besteht aus einem rechteckigen oder quadratischen Rastergitter mit Pfeilen. Ziel ist es, einen Weg durch das Rastergitter zu finden, indem man jedes Feld einmal besucht. Der Pfad beginnt von dem Feld mit der Nummer 1. Der Pfad kann in horizontaler, vertikaler oder diagonaler Richtung von einem Feld zum anderen springen, jedoch nur in Richtung des Pfeils. Einige Nummern wurden bereits vergeben.

Pfeilnetz ("Arrow Web") ist ein Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter ist mit Pfeilen gefüllt. Ziel ist es, einige der Pfeile so zu schwärzen, dass jeder Pfeil im Rastergitter auf genau einen geschwärzten Pfeil zeigt.

Hanare ("Hanaregumi"; aus dem Japanischen, wörtlich "Familienpaar") ist ein Logikpuzzle. Ein quadratisches oder rechteckiges Rastergitter ist in Bereiche unterteilt. Das Ziel ist, eine Zahl in jedem Bereich zu platzieren. Eine Zahl ist gleich der Größe des Bereichs. Der Abstand zwischen zwei horizontal oder vertikal benachbarten Zahlen muss gleich sein der Differenz dieser Zahlen.

Oasen ("Oases") ist ein logisches Rätsel. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise mit Zahlen in einigen Feldern. Das Ziel besteht darin, einige Felder schwarz zu machen (wobei die anderen Felder weiß bleiben), so dass die nicht geschwärzten Felder horizontal oder vertikal miteinander verbunden sind. Geschwärzte Felder dürfen keinen Rand gemeinsam haben. Felder mit Kreisen dürfen nicht geschwärzt werden. Weiße Felder dürfen keinen Bereich der Größe 2 x 2 abdecken. Eine Zahl in einem Kreis repräsentiert die Anzahl der anderen Kreise, die von diesem Kreis aus erreicht werden können, indem nur leere (d.h. weiße Felder ohne Kreise) Felder durchlaufen werden. (Ein Kreis, der auf mehreren Wegen erreicht werden kann, zählt nur als ein Kreis.)

Kaninchen und Bäume ("Rabbits and Trees"; auch bekannt als "Raitonanba", "Light Number") ist ein quadratisches Rastergitter mit Zahlen in einigen Feldern. Die Aufgabe ist es, in jede Zeile und in jede Spalte genau einen weißen Kreis ("Hase") und einen schwarzen Kreis ("Baum") zu platzieren. Eine Zahl gibt an, wie viele weiße Kreise ("Kaninchen") in der entsprechenden Zeile und Spalte zu sehen sind. Ein Kaninchen ist nur sichtbar, wenn es nicht hinter einem Baum versteckt ist.

Sternenhimmel ("Stars and Arrows", Sterne und Pfeile) besteht aus einem rechteckigen oder quadratischen Rastergitter mit Pfeilen in einigen Feldern. Ziel ist es, Sterne in leere Felder zu setzen. Jeder Pfeil zeigt auf genau einen Stern und jeder Stern wird durch genau einen Pfeil angezeigt. Zahlen außerhalb des Rastergitters zeigen die Anzahl der Sterne in der entsprechenden Zeile oder Spalte.

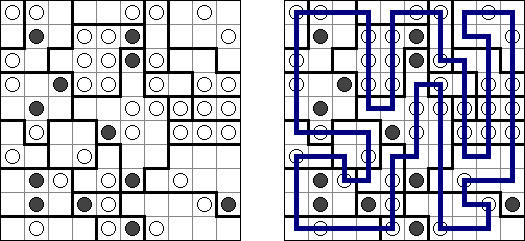
Kanjo ("Kanjo-sen supesharu"; aus dem Japanischen, wörtlich "spezieller Rundweg") ist ein logisches Puzzle. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise mit Zahlen in einigen Feldern. Ziel ist es, Rundwege einzuzeichnen, die alle Felder richtig durchlaufen. Ein Rundweg kann sich selbst oder andere Rundwege kreuzen. Alle vorgegebenen Linienstücke müssen als Teil eines Rundwegs verwendet werden. Felder mit derselben Zahl gehören zum selben Rundweg. Felder mit unterschiedlichen Zahlen gehören zu verschiedenen Rundwegen. Ein Rundweg muss durch mindestens ein Feld mit einer Zahl gehen (es gibt genau so viele Rundwege, wie das Rastergitter unterschiedliche Zahlen enthält).

Rukkuea ("Look-Air", Sichtlinie) ist ein von Nikoli erfundenes Logikpuzzle. Das Puzzle besteht aus einem rechteckigen oder quadratischen Rastergitter mit Zahlen in einigen Feldern. Die Aufgabe ist, einige Felder nach den folgenden Regeln zu schwärzen:

• Schwarze Felder bilden eine quadratische Fläche.
• Keine schwarzen Quadrate berühren sich horizontal oder vertikal (nur diagonal).
• Schwarze Quadrate gleicher Größe dürfen sich nicht "sehen": Horizontale oder vertikale Linien zwischen zwei schwarzen Quadraten müssen mindestens ein schwarzes Quadrat anderer Größe enthalten.
• Jede Zahl gibt an, wie viele der fünf Felder (die mit der Anzahl plus die vier orthogonal benachbarten Felder) geschwärzt werden sollten.

Golem Grad (eine Insel im Prespa-See in der Republik Nordmazedonien) vereint die Regeln der Nurikabe- und Snake-Rätsel (Schlangen-Rätsel). Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Kreise und Zahlen. Ziel ist es, einige Felder nach den folgenden Regeln zu schwärzen:

• Die schwarzen Felder teilen das Rastergitter in Bereiche mit weißen Feldern ("Inseln") auf, die jeweils höchstens eine Zahl enthalten.
• Zwei Inseln dürfen nicht miteinander verbunden sein.
• Die Insel muss so viele weiße Felder haben wie die Zahl, die sie enthält.
• Alle schwarzen Felder müssen einen orthogonal zusammenhängenden Bereich bilden.
• Kein 2 x 2-Felderbereich innerhalb des Rastergitters darf schwarz sein.
• Alle schwarzen Felder müssen in "Schlangen" teilbar sein, wobei die Köpfe und Schwänze als Kreise im Rastergitter angegeben sind.
• Schlangen dürfen sich nicht kreuzen.

Trilogik ("Trilogy") besteht aus einem quadratischen oder rechteckigen Rastergitter mit Symbolen in einigen Feldern: Quadrate, Kreise, Dreiecke. Ziel ist es, jedes Feld mit einem Symbol zu füllen. Drei aufeinanderfolgende Symbole dürfen in keiner Zeile, Spalte oder Diagonale alle gleich sein noch dürfen alle unterschiedlich sein.

Grades ist ein logisches Rätsel. Das Ziel ist, Zahlen in einigen Feldern eines quadratischen oder rechteckigen Rastergitters gemäß folgenden Regeln zu platzieren:

• Keine zwei horizontal, vertikal oder diagonal nebeneinander liegenden Felder enthalten eine Zahl.
• Die Zahlen oben und links entsprechen den Zeilen- und Spaltensummen der Felder mit Zahlen.
• Die Zahlen unten und rechts sind die Summen der Zahlen in den Zeilen und Spalten.

Hukuwall ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Buchstaben. Ziel ist es, in jedes leere Feld eine horizontale oder vertikale Linie zu zeichnen. Jeder Buchstabe steht für eine Zahl: Alle gleichen Buchstaben müssen durch die gleiche Zahl ersetzt werden, verschiedene Buchstaben müssen durch verschiedene Zahlen ersetzt werden. Eine Zahl in einem Feld gibt die Gesamtlänge der Linien an, die an den Rändern dieses Feldes enden. Eine Linie kann nicht zwei Felder mit Buchstaben verbinden. Die Anzahl der Linienrichtungen, die aus demselben Buchstaben kommen, sind alle unterschiedlich.

Nurimisaki (aus dem Japanischen, wörtlich "ein Kap malen") ist ein von Nikoli erfundenes Logikpuzzle. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Kreise. Ein Kreis kann eine Zahl enthalten oder nicht. Die Aufgabe besteht darin, einige Felder des Rastergitters gemäß den folgenden Regeln zu schwärzen:

• Weiße Felder bilden einen Pfad, der genau ein Feld breit ist.
• Felder mit Kreisen sind immer weiß.
• Ein Feld mit einem Kreis muss an seiner Seite genau ein weißes Feld haben.
• Ein weißes Feld ohne Kreis muss mindestens zwei orthogonal benachbarte weiße Felder aufweisen.
• Eine Zahl in einem Kreis gibt an, wie viele weiße Felder horizontal und vertikal von diesem Feld aus gesehen werden können, einschließlich des Feldes selbst.
• Alle weißen Felder müssen horizontal oder vertikal verbunden sein.
• Kein Bereich von 2 x 2 Feldern darf dieselbe Farbe haben.

Sternennacht ("Starry Night"; auch bekannt als "Niapuresu", "Near Place") ist ein von Naoki Inaba (Japan) erfundenes Logikpuzzle. Ziel ist es, einen weißen Kreis ("Sonne"), einen schwarzen Kreis ("Mond") und einen Stern in jede Reihe und Spalte des Rastergitters zu setzen. Gleiche Figuren dürfen sich nicht diagonal berühren. Die Zahlen außerhalb des Rastergitters geben den Abstand zwischen dem Stern und den Kreisen in dieser Zeile oder Spalte an:

• Der weiße Kreis zeigt an, dass die Sonne näher am Stern ist als der Mond.
• Der schwarze Kreis zeigt an, dass der Mond näher am Stern ist als die Sonne.
• Der Stern außerhalb des Rastergitters zeigt an, dass die Kreise in dieser Zeile oder Spalte gleich weit vom Stern entfernt sind.

Douieru (aus dem Japanischen, wörtlich "gleich und verschieden") ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Kreise. Ziel ist es, das Rastergitter in L-förmige Gebiete zu unterteilen. Die beiden "Beine" eines Gebietes müssen genau ein Feld breit sein. Ein Kreis stellt ein Feld dar, in dem sich ein "L" knicken muss (das Rastergitter enthält Kreise für alle Gebiete). Wenn eine Feld einen Doppelkreis enthält, müssen die beiden Beine des Gebietes dieselbe Länge haben. Ein schwarzer Kreis bedeutet eine unterschiedliche Beinlänge. Wenn ein Feld einen weißen Kreis enthält, ist das Verhältnis der Beinlängen unbekannt.

Tetoron ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Symbole. Ziel ist es, das Gitter in Gebiete von genau vier Feldern (Tetromino) zu unterteilen. Jedes Gebiet enthält genau zwei verschiedene Symbole. Gebiete gleicher Form müssen die gleichen Symbole enthalten. Die Tetrominos können gedreht oder gespiegelt werden.

Sashikaku (aus dem Japanischen, wörtlich "Bereich nach Differenz") ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, das Rastergitter in rechteckige und quadratische Bereiche zu unterteilen, sodass jeder Bereich genau eine Zahl enthält und diese Zahl die Differenz zwischen Breite und Höhe des Bereichs darstellt.

Heki ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, das Rastergitter in Bereiche mit jeweils sechs Feldern zu unterteilen. Jeder Bereich enthält genau zwei Zahlen. Die Zahl gibt an, wie viele Felder desselben Bereichs orthogonal zu dem Feld mit der Zahl benachbart sind.

Castle Wall ist ein Logikrätsel, das von Palmer Mebane (USA) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze oder umrandete Felder. Einige von ihnen enthalten Zahlen und Pfeile. Ziel ist es, einen einzigen, geschlossenen, sich nicht überschneidenden Rundweg zu zeichnen. Schwarze Felder müssen außerhalb des Rundwegs liegen; weiß umrandete Felder müssen sich innerhalb des Rundwegs befinden; für graue Felder ist diese Information unbekannt. Zahlen und Pfeile beziehen sich auf die Gesamtlänge der Rundweg-Segmente in Pfeilrichtung. (Mit anderen Worten, die Zahl gibt an, wie viele Feldränder in Pfeilrichtung von dem Rundweg überschritten werden.)

Deddoanguru ("Dead Angle", "Toter Winkel") ist ein von Naoki Inaba (Japan) erfundenes Logikpuzzle. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze Kreise mit Zahlen. Ziel ist es, das Gitter in Gebiete aufzuteilen. Jedes Gebiet enthält einen schwarzen Kreis. Ein schwarzer Kreis ist ein Auge, das in alle vier Richtungen schaut, bis zu einer Bereichsgrenze. Die Zahl im Feld gibt an, wie viele Felder des Gebiets das Auge nicht sieht.

Endorain ("End Line") ist ein Logikrätsel, das von Naoki Inaba (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Ziel ist es, horizontale und vertikale Linien zwischen den Mittelpunkten der Felder zu zeichnen. Jede Linie verbindet zwei Felder in verschiedenen Gebieten. Eine Zahl in einem Gebiet gibt an, wie viele Linien in diesem Gebiet beginnen/enden. Alle Felder müssen von den Linien verwendet werden.

Nuraf ("Araf Nurikabe") kombiniert die Regeln von Nurikabe und Araf Puzzles. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder teilen das Rastergitter in Gebiete von weißen Feldern ("Inseln").
• Felder mit Zahlen sind immer weiß.
• Zwei Inseln dürfen nicht verbunden sein.
• Alle schwarzen Felder müssen verbunden sein.
• Kein Bereich von 2 x 2-Feldern innerhalb des Rastergitters darf die schwarze Farbe haben.
• Jede Insel enthält genau zwei Zahlen. Eine Insel muss ein Gebiet haben, das genau zwischen diesen Zahlen liegt. Wenn die Insel beispielsweise 1 und 4 enthält, muss die Inselfläche 2 oder 3 betragen.

Miti (aus dem Japanischen, wörtlich "Straße") ist ein Logikrätsel, das von Nishiyama Yukari (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Punkte an einigen Schnittpunkten der Gitterlinien. Ziel ist es, einige Grenzenlinien zwischen den Zellen zu schwärzen. In jedem gegebenen Rasterpunkt müssen genau drei schwarze Linien zusammentreffen. In allen anderen Rasterpunkten dürfen höchstens zwei schwarze Linien zusammenlaufen. Alle Felder des Rastergitters bilden einen einzigen geschlossenen Rundweg ohne Sackgassen, genau ein Feld breit.

Arofuro ("Arrow Flow") ist ein Logikrätsel, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, in jedem leeren Feld Pfeile zu platzieren, die in vier Richtungen zeigen.

• In benachbarten Feldern dürfen nicht dieselben Pfeile platziert werden.
• Beginnen Sie in einem Feld mit einem Pfeil und folgen Sie den Pfeilen von Feld zu Feld, um ein Feld mit einer Zahl zu erreichen.
• Ein Feld mit einer Zahl gibt die Gesamtzahl der Pfeile an, die zu diesem Feld führen.

Zwischenknick (auch bekannt als "Every Second Turn", "Every Second Breakpoint", "Alternate Corners") ist ein rechteckiges oder quadratisches Rastergitter mit Kreisen in einigen Feldern. Ziel ist es, einen einzelnen kontinuierlichen, sich nicht schneidenden Rundweg zu zeichnen, der jedes Feld genau einmal besucht. Bei jedem Feld mit einem Kreis wird eine 90-Grad-Wendung ausgeführt. Es gibt genau eine Abknickung zwischen zwei aufeinanderfolgenden Kreisen, die der Rundweg besucht.

Mobiriti ("Mobility") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise mit Zahlen in einigen Feldern. Ziel ist es, einige Felder eines Rastergitters zu schwärzen. Felder mit Kreisen können nicht geschwärzt werden. Eine Zahl in einem Kreis gibt an, wie viele leere weiße Felder von diesem Feld aus erreicht werden können, indem Sie sich horizontal oder vertikal bewegen.

Mubunanba ("Move Number") ist ein von Naoki Inaba (Japan) erfundenes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Federn Zahlen. Ziel ist es, einige Blöcke im Rastergitter mit der Größe von genau drei Feldern zu lokalisieren. Das Rastergitter kann Felder enthalten, die zu keinem Block gehören. Jeder Block enthält genau eine Zahl. Eine Zahl gibt die Anzahl der möglichen Richtungen an, in die ein Block verschoben werden kann.

Terra-X besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Regionen unterteilt ist. Ziel ist es, in jede Region eine Zahl von 0 bis 9 so zu platzieren, dass Regionen mit gleicher Anzahl keine Kante gemeinsam haben (sie dürfen sich diagonal berühren). Für jeden Gitterpunkt, an dem vier Regionen aufeinander treffen, muss die Summe der Zahlen in diesen Regionen 10 betragen. (Alle diese Gitterpunkte sind mit einem kleinen schwarzen Punkt markiert).

Rimotoejji ("Remote Edge", "Ferne Kante") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Das Ziel ist, alle Punkte durch einen einzigen kontinuierlichen, sich nicht überkreuzenden Rundweg zu verbinden. Alle Pfeile und Kreuze sollen sich innerhalb des Rundwegs befinden. Ein Pfeil zeigt in Richtung der längsten geraden Folge von Feldern, die von diesem Feld aus sichtbar sind. Ein Kreuz wird in der Mitte von mehr als einer längsten geraden Folge von Feldern innerhalb des Rundwegs platziert.

Double Back besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete unterteilt ist. Ziel ist es, einen einzelnen geschlossenen Rundweg aus horizontalen und vertikalen Segmenten zu zeichnen, der durch alle weißen Felder verläuft. Jedes Gebiet muss genau zweimal besucht werden. Das Rastergitter kann schwarze Felder enthalten. Der Rundweg darf kein schwarzes Feld passieren.

Wamuzu ("Worms", "Würmer") ist ein von Naoki Inaba (Japan) erfundenes Logikrätsel. Es besteht aus einem Rastergitter mit Kreisen in einigen Feldern. Ziel ist es, Kreise paarweise zu verbinden, indem eine Linie gezeichnet wird, die horizontal und vertikal durch die Mittelpunkte der Felder verläuft. Alle Felder müssen von den Linien verwendet werden. Alle Abschnitte jeder Linie müssen einer Feldlänge entsprechen.

Kaero ("Ouchihekaero"; aus dem Japanischen wörtlich "Lass uns nach Hause gehen") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erstellt wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Ziel ist es, einige Buchstaben horizontal oder vertikal so zu verschieben, dass alle Buchstaben in einem Gebiet gleich sind. Die Buchstaben dürfen die Spuren anderer Buchstaben nicht kreuzen und sich nicht über andere Buchstaben bewegen.

Kapama (aus dem Türkischen, wörtlich "Schließen") besteht aus einem rechteckigen oder quadratischen Rastergitter mit diagonalen Linien in einigen Feldern. Ziel ist es, einige Felder zu schwärzen, um Figurenpaare (Zwillingsformen) zu erzeugen. Zwillingsformen sind in Bezug auf eine diagonale Linie symmetrisch. Zwillingsformen sind mit einer diagonalen Linie verbunden. Keine zwei Formen dürfen eine Kante teilen. Felder mit diagonalen Linien dürfen nicht geschwärzt werden. Zahlen außerhalb des Rastergitters geben die Anzahl der schwarzen Felder in der entsprechenden Zeile oder Spalte an.

Yunikumaka ("Unique Marker", "Eindeutige Markierung") ist ein von Naoki Inaba (Japan) erfundenes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält Punkte. Ein Punkt kann sich in der Mitte eines Feldes oder an einer Grenze zwischen benachbarten Feldern befinden. Ziel ist es, ein Rastergitter in Regionen mit genau vier Feldern (Tetrominos) aufzuteilen. Jede Region enthält genau einen Punkt entweder in der Mitte eines Feldes oder an einer Grenze zwischen zwei Feldern. Punkte an den Grenzen zwischen Regionen werden ignoriert. Schwarze Felder gehören keiner Region an.

Mäanderzahlen ("Meandering Numbers", "Count Number", "Worms") werden auf einem rechteckigen oder quadratischen Rastergitter gespielt, das in Regionen unterteilt ist. Ein Raster kann in einigen Feldern Zahlen enthalten. Jede Region muss mit jeder der Zahlen von 1 bis N gefüllt sein, wobei N die Anzahl der Felder in der Region ist. Felder mit den gleichen Zahlen dürfen nicht orthogonal oder diagonal benachbart sein. Aufeinanderfolgende Zahlen innerhalb einer Region sind orthogonal benachbart. (Für jede Region muss es möglich sein, einen Pfad zu zeichnen, der bei 1 beginnt und bei N endet und genau einmal und in numerisch aufsteigender Reihenfolge durch die einzelnen Felder verläuft.)

Yokibunkatsu (aus dem Japanischen, wörtlich "Container-Unterteilung") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Sterne. Ziel ist es, das Rastergitter in Gebiete mit genau fünf Feldern zu unterteilen. Jedes Gebiet enthält einen Stern. Die Felder des Gebiets müssen zu einem Würfel faltbar sein, mit dem Stern unten und ohne Oberseite ("Dach"). Einige Grenzabschnitte zwischen Gebieten wurden bereits angegeben. Das Rastergitter kann Felder enthalten, die zu keinem Gebiet gehören.

Scrin ("Screen", "Bildschirm") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Kreise (leer oder mit Zahlen). Ziel ist es, das Rastergitter in rechteckige Bereiche zu unterteilen. Jeder Bereich enthält nicht mehr als einen Kreis. Das Rastergitter kann Bereiche ohne Kreise enthalten. Ein Bereich muss dieselbe Anzahl von Feldern haben wie die Zahl in dem Kreis. Bereiche dürfen keine Kante teilen. Bereiche müssen einen einzigen nicht verzweigten Rundweg bilden, in dem sich alle Bereiche an den Ecken berühren.

Eins bis X ("From 1 To X") besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete unterteilt ist. Jedes Gebiet muss mit jeder der Zahlen von 1 bis zur Anzahl der Felder in dem Gebiet gefüllt sein. Gleiche Zahlen dürfen nicht orthogonal benachbart sein. Zahlen außerhalb des Rastergitters zeigen die Summen der Zahlen in der entsprechenden Zeile oder Spalte an.

Shingoki (aus dem Japanischen wörtlich "Verkehrsampel") ist ein rechteckiges oder quadratisches Rastergitter mit Kreisen in einigen Feldern. Ziel ist es, einen einzelnen kontinuierlichen, sich nicht schneidenden Rundweg zu zeichnen, der durch alle Kreise verläuft. In schwarzen Kreisen muss rechtwinklig abgebogen werden, weiße Kreise müssen gerade durchlaufen werden. In einem Feld mit einem grauen Kreis kann der Rundweg abbiegen oder nicht. Wenn ein Kreis eine Zahl enthält, gibt diese Zahl die Gesamtlänge der geraden Linien an, die aus dem Kreis herausgehen.

Stitches besteht aus einem rechteckigen oder quadratischen Rastergitter, das in Gebiete unterteilt ist. Ziel ist es, jedes Gebiet mit allen Nachbargebieten mit genau einer Linie zu verbinden ("Stich"). Die Länge jeder Linie entspricht einer Feldlänge (sie verbindet zwei orthogonal benachbarte Felder von verschiedenen Gebieten). Ein Feld darf höchstens von einer Linie besucht werden. Eine Zahl am Rand des Rastergitters gibt an, wie viele Linienendpunkte in der entsprechenden Zeile oder Spalte platziert werden müssen.

Cross+A kann Rätsel mit 2, 3 oder 4 Linien lösen, die Nachbarregionen verbinden.

Neibadomino ("Neighbour Domino", "Nachbar-Domino") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, einige Blöcke im Rastergitter mit der Größe von genau zwei Feldern ("Dominosteine") zu lokalisieren und Blöcke mit Zahlen zu füllen. Das Rastergitter kann Felder enthalten, die zu keinem Block gehören. Jede Zahl im Raster sollte Teil eines Blocks sein und die Anzahl der orthogonal benachbarten Dominosteine ​​angeben. Blöcke mit den gleichen Zahlen dürfen nicht orthogonal benachbart sein. Blöcke dürfen nicht einen Bereich von 2 x 2 Feldern bedecken. (Das Rastergitter kann Bereiche von 2 x 2 Feldern ohne Blöcke enthalten.)

Jemini ("Jemini Block") ist ein logisches Puzzle, das von Naoki Inaba (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Buchstaben in einigen Feldern. Ziel ist es, das Rastergitter so in Gebiete zu unterteilen, dass jedes Gebiet genau einen Buchstaben enthält. In Gebieten gleicher Größe, Form und Ausrichtung muss sich derselbe Buchstabe genau an derselben Position befinden.

Doppel-Schokolade ("Double Choco") ist ein von Nikoli veröffentlichtes Logik-Puzzle. In einem rechteckigen oder quadratischen Rastergitter ist genau die Hälfte der Felder grau gefärbt. Ziel ist es, das Rastergitter in Gebiete zu unterteilen. Jedes Gebiet muss einen Bereich mit weißen Feldern und einen Bereich mit grauen Feldern enthalten. Ein Gebietspaar muss dieselbe Form und Größe haben (die Gebiete können gedreht oder gespiegelt sein). Eine Zahl gibt an, wie viele Felder derselben Farbe das Gebiet enthält. Ein Gebiet kann mehr als ein Feld mit einer Zahl enthalten (in diesem Fall enthalten die Felder dieselbe Zahl).

Konarupu ("Corner Loop") ist ein Logikrätsel, das von Naoki Inaba (Japan) erfunden wurde. Das Ziel besteht darin, einen kontinuierlichen, sich nicht überschneidenden Rundweg zu erstellen, der horizontal oder vertikal von einem Punkt zu einem benachbarten Punkt verläuft. Eine Zahl in einem Feld gibt an, in wie vielen der umgebenden Punkte der Rundweg um 90 Grad abbiegt.

Gaidoaro ("Guide Arrow") ist ein Logikrätsel von Naoki Inaba (Japan). Ein rechteckiges oder quadratisches Rastergitter enthält Pfeile und einen einzelnen Stern. Ziel ist es, einige Felder zu schwärzen, so dass die weißen Felder horizontal oder vertikal miteinander verbunden sind. Geschwärzte Felder sollten keine Kante teilen. Felder mit Pfeilen oder einem Stern dürfen nicht geschwärzt werden. Ein Pfeil zeigt die Richtung an, in die Sie sich bewegen müssen, um einen Stern zu erreichen, indem Sie nur durch weiße Felder gehen (es darf nur einen Weg von jedem weißen Feld geben, um ein Feld mit einem Stern zu erreichen).

Mittelweg ("Mid-Loop") ist ein Logikrätsel von Nikoli. Ein rechteckiges oder quadratisches Rastergitter enthält Punkte; ein Punkt kann in der Mitte eines Feldes oder an einer Grenze zwischen benachbarten Feldern liegen. Das Ziel besteht darin, einen einzigen kontinuierlichen, sich nicht überschneidenden Rundweg zu zeichnen, der alle Punkte exakt durchläuft. Punkte müssen direkt durchlaufen werden. Segmente einer geraden Linie, die aus einem Punkt herausgehen, müssen gleich sein.

Dotchi-Loop ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter ist in Regionen unterteilt. In einigen Feldern enthält das Rastergitter weiße und schwarze Kreise. Das Ziel ist, einen einzigen, sich nicht überschneidenden Rundweg zu zeichnen. Der Rundweg muss alle Felder mit weißen Kreisen besuchen; er darf nicht durch einen schwarzen Kreis gehen. Der Rundweg verläuft entweder gerade durch alle weißen Kreise oder macht eine 90-Grad-Abbiegung bei allen weißen Kreisen in einer Region.

Trinairo ist ein Logikrätsel, das von Leo de Winter (Niederlande) erfunden wurde. Ziel ist es, ein 9 x 9 großes Rastergitter so mit Buchstaben zu füllen, dass jede Zeile und jede Spalte drei Buchstaben A, drei Buchstaben B und drei Buchstaben C enthält. Ist ein Feld mit einer anderen Farbe markiert, unterscheidet sich ein Buchstabe in diesem Feld von den Buchstaben in allen orthogonal benachbarten Feldern.

Detour ist ein Logikpuzzle. Es enthält ein rechteckiges oder quadratisches Rastergitter, das in Regionen unterteilt ist. Das Ziel ist, einen einzigen kontinuierlichen, sich nicht überschneidenden Rundweg zu zeichnen, der jedes Feld genau einmal besucht. Jede Zahl in einer Region gibt an, wie oft der Rundweg in der Region abbiegt.

Balance Loop ist ein Logikpuzzle, das von Prasanna Seshadri (Indien) entwickelt wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern schwarze und weiße Kreise. Ziel ist es, einen einzelnen durchgehenden, sich nicht schneidenden Rundweg zu zeichnen, der alle Felder mit Kreisen besucht. Rundwegsegmente, die von einem weißen Kreis ausgehen, sind gleich lang, während die Rundwegsegmente, die von einem schwarzen Kreis ausgehen, dies nicht sind. Wenn ein Kreis eine Zahl enthält, gibt sie die Summe der Rundwegsegmentlängen auf beiden Seiten des Kreises an.

Turf ist ein Logikpuzzle, das von John Bulten (USA) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Das Ziel besteht darin, einige Felder zu schattieren, sodass das Rastergitter in graue und weiße Regionen unterteilt wird. Jede Region muss mindestens eine Zahl enthalten. Diese Zahl gibt die Größe einer Region an. Wenn eine Region ein anderes Feld mit einer Zahl enthält, stellt sie dar, wie viele umgebende Felder weiß sind, einschließlich sich selbst und der diagonalen Felder.

SquarO ist ein Logik-Puzzle ähnlich wie Minesweeper. Ein rechteckiges oder quadratisches Rastergitter enthält Punkte auf den Schnittpunkten von Linien. Eine Zahl in einem Feld gibt an, wie viele der vier umgebenden Punkte schwarz sind.

Chiyotsui (aus dem Japanischen wörtlich "Türscharnier") ist ein Logikpuzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete unterteilt. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Schwarze Felder bilden Bereiche. Jeder Bereich erstreckt sich über genau zwei Gebiete, seine Teile sind symmetrisch zur Gebietsgrenze.
• Ein Feld mit einer Zahl gibt an, wie viele Felder in dem Gebiet geschwärzt werden müssen.
• Keine zwei schwarzen Bereiche dürfen eine gemeinsame Kante haben.

Aqre ist ein von Eric Fox (USA) erfundenes Logikpuzzle. Ein rechteckiges oder quadratisches Rastergitter ist in Regionen unterteilt. Ziel ist es, einige Felder des Rastergitters so zu schwärzen, dass alle schwarzen Felder eine orthogonal zusammenhängende Fläche bilden. Ein Feld mit einer Zahl gibt an, wie viele Felder in der Region geschwärzt werden müssen. In Regionen ohne Nummer können beliebig viele Felder geschwärzt werden (alle Felder können weiß bleiben). Es dürfen nicht mehr als drei schwarze oder weiße Felder in einer Reihe im Rastergitter vorkommen.

Geradeweg ("Straight Loop") ist ein Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise mit Zahlen in einigen Feldern. Die Aufgabe besteht darin, einen einzelnen geschlossenen, sich nicht schneidenden Rundweg zu zeichnen, der durch alle Kreise verläuft. Die Zahl gibt die Länge des geraden Segments an, das durch den Kreis geführt wird. Wenn der Rundweg in einem Zahlenfeld abbiegt, müssen beide geraden Segmente die gleiche Länge haben, wie die Zahl angibt.

Kuroclone ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter wird in Regionen unterteilt. Ziel ist es, einige Felder des Rasters zu schwärzen. Jede Region muss zwei Bereiche mit schwarzen Feldern enthalten: Dieses Bereichspaar muss dieselbe Form und Größe haben (die Bereiche können gedreht oder gespiegelt sein). Felder mit Zahlen sind immer weiß. Der Pfeil zeigt auf ein benachbartes Feld, das zu einem schwarzen Bereich gehört. Die Zahl gibt die Größe dieses Bereichs an. Wenn zwei Felder über eine Regionsgrenze hinweg orthogonal benachbart sind, muss mindestens ein Feld weiß sein.

Yajisan-Sokoban ist ein Logikrätsel, das von Jamie Hargrove erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter enthält graue Quadrate. Die Aufgabe besteht darin, die grauen Quadrate vertikal oder horizontal zu verschieben (einige Quadrate können unverändert bleiben). Graue Quadrate dürfen die Bahnen anderer grauer Quadrate nicht kreuzen und sich nicht über andere Quadrate bewegen (graue Quadrate können durch nummerierte Felder gehen). Ein Feld mit einer Zahl und einem Pfeil stellt dar, wie viele graue Quadrate sich in der Reihe oder Spalte befinden, auf die der Pfeil zeigt. Befindet sich über einem nummerierten Feld ein graues Quadrat, spielt es im Rätsel keine weitere Rolle und kann wahr oder falsch sein. Wenn ein graues Quadrat durch ein Feld mit einer Zahl und einem Pfeil geht, liefert dieses nummerierte Feld wahre Informationen.

Linien-Segmente ("Line Segment") ist ein Logikrätsel, das von Erich Friedman (USA) erfunden wurde. Die Aufgabe besteht darin, Liniensegmente zu zeichnen, die durch genau 3 oder 4 aufeinanderfolgende Felder verlaufen. Die Liniensegmente können nur horizontal (H), vertikal (V) oder diagonal (D) sein. Jedes Feld muss genau einmal besucht werden. Ein Feld mit einem Buchstaben enthält ein Liniensegment mit dieser Ausrichtung.

Raneko ("Ranekomappu"; aus dem Japanischen wörtlich "Katzenlebensraumkarte") ist ein Logikrätsel, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter enthält Kreise (mit oder ohne Zahl). Ziel ist es, das Rastergitter in Gebiete aufzuteilen. Jedes Gebiet enthält einen Kreis ("Katze"). Ein Kreis mit einer Zahl zeigt die Größe eines Gebietes an. Ein Rastergitter kann schwarze Felder enthalten. Die Zahl in einem schwarzen Feld gibt an, wie viele Gebiete eine Kante mit diesem schwarzen Feld teilen.

Faktorism ("Find the Factors") ist ein Logikrätsel, das von Iva Sallay (USA) erfunden wurde. Ziel ist, auf dem quadratischen Rastergitter N x N jeweils in der oberen Zeile und in der linken Spalte die Zahlen von 1 bis N zu platzieren. Eine Zahl in einem Feld gibt das Produkt der Zahlen außerhalb des Rastergitters in der entsprechenden Zeile und Spalte an.

Akiperago ("Archipelago") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze Felder; einige von ihnen enthalten Zahlen. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder bilden "Inseln". Keine zwei Inseln dürfen einen gemeinsamen Rand haben; Inseln können durch ihre Ecken miteinander verbunden werden.
• Wenn eine Insel ein nummeriertes Feld enthält, stellt diese Zahl die Anzahl der schwarzen Felder auf der Insel dar. Eine Insel kann ein paar nummerierte Felder enthalten (alle Zahlen innerhalb einer Insel sind gleich).
• Alle Inseln bilden "Archipele". Ein Archipel ist eine Gruppe von zwei oder mehr Inseln, die durch ihre Ecken verbunden sind.
• Wenn ein Archipel N Inseln enthält, bestehen sie aus 1 bis N Feldern (nicht unbedingt in dieser Reihenfolge).

Yakazu ist ein Logikrätsel, das von Patrick Tirone erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter wird teilweise durch schwarze Felder in Fächer unterteilt. Ziel ist es, alle weißen Felder mit Zahlen zu füllen. Jedes Fach, vertikal oder horizontal, muss eine Reihe fortlaufender Nummern enthalten, jedoch in beliebiger Reihenfolge (z. B.: 4-1-3-2). Jedes Fach mit zwei oder mehr Feldern muss alle Zahlen beginnend mit 1 enthalten.

Miraringutairu ("Mirroring Tile") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält schwarze Felder; einige von ihnen enthalten Zahlen. Ziel ist es, Blöcke von schwarzen Feldern im Rastergitter zu lokalisieren. Jedes nummerierte Feld gibt die Gesamtzahl der schwarzen Felder im Block an (ein Block kann mehrere nummerierte Felder mit der gleichen Zahl enthalten). Das Rastergitter kann Blöcke ohne Zahlen enthalten. Keine zwei Blöcke dürfen eine gemeinsame Kante haben, aber jeder Block muss mit mindestens einem anderen Block gleicher Größe und Form an seinen Ecken verbunden sein (Blöcke dürfen gedreht oder gespiegelt sein).

Heyablock ("Heyawake-Block") ist ein Logikpuzzle, das von Atsumi Hirose (Japan) erfunden wurde. Ein rechteckiges oder quadratisches Rastergitter wird in Regionen unterteilt. Ziel ist es, einige Zellen eines Rasters nach folgenden Regeln zu schwärzen:

• Alle schwarzen Felder einer Region müssen verbunden sein.
• Ein Feld mit einer Zahl gibt an, wie viele Felder in der Region geschwärzt werden müssen.
• In Regionen ohne Nummer dürfen beliebig viele Felder geschwärzt werden (mindestens eines).
• Wenn zwei Felder über eine Regionsgrenze hinweg orthogonal benachbart sind, muss mindestens ein Feld weiß sein.
• Alle weißen Felder bilden einen orthogonal zusammenhängenden Bereich.
• Eine Reihe verbundener weißer Felder kann nicht durch zwei oder mehr Regionsgrenzen gehen.

Choco-Banana ist ein von Nikoli veröffentlichtes Logikpuzzle. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, einige Felder des Rastergitters zu schwärzen. Ein Gebiet aus schwarzen Feldern muss ein Rechteck oder Quadrat bilden. Ein Gebiet aus weißen Feldern darf kein Rechteck oder Quadrat bilden. Wenn ein schwarzes oder weißes Gebiet eine Zahl enthält, gibt dies die Größe dieses Gebiets an. Ein Gebiet kann mehr als ein Feld mit einer Nummer enthalten.

Wataridori (aus dem Japanischen wörtlich "Zugvögel") ist ein Logikpuzzle, das von Nikoli veröffentlicht wurde. Ein rechteckiges oder quadratisches Rastergitter wird in Gebiete unterteilt. Das Rastergitter enthält in einigen Feldern Kreise (leer oder mit Zahlen). Ziel ist es, Kreise paarweise zu verbinden, indem eine Linie gezogen wird, die horizontal und vertikal durch die Mittelpunkte der Felder verläuft. Ein Feld darf höchstens einmal von einer Linie besucht werden. Eine Linie kann Kreise mit gleichen Zahlen oder leere Kreise verbinden oder eine Linie kann zwischen einem leeren Kreis und einem Kreis mit einer Zahl gezogen werden. Eine Zahl in einem Kreis gibt an, wie viele Gebiete von der Linie besucht werden. Ein Gebiet darf höchstens einmal von der Linie besucht werden.

Chenburo ("Chain Block", "verkettete Blöcke") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein Rastergitter enthält in einigen Feldern Zahlen oder Fragezeichen. Ziel ist es, einige Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Die schwarzen Felder bilden Blöcke. Keine Blöcke berühren sich horizontal oder vertikal (nur diagonal).
• Eine Zahl gibt die Anzahl der schwarzen Felder im Block an. Anstelle von Hinweisnummern können auch Fragezeichen verwendet werden. Jedes Fragezeichen kann eine beliebige ganze Zahl ungleich Null darstellen.
• Jeder Block enthält genau eine Zahl oder ein Fragezeichen.
• Alle Blöcke bilden "Ketten". Eine Kette ist eine Gruppe von zwei oder mehr Blöcken, die durch ihre Ecken verbunden sind.
• Zwei Blöcke, die zur gleichen Kette gehören, dürfen nicht die gleiche Form und Größe haben, wobei Rotationen und Reflexionen als gleich gezählt werden.

Wanrumuwandoa ("One Room One Door", "mit einem Raum und einer Tür") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter ist in Gebiete ("Räume") unterteilt. Ein Gebiet kann ein Feld mit einer Zahl enthalten. Das Ziel ist, einige Felder eines Rastergitters nach den folgenden Regeln zu schwärzen:

• Ein Feld mit einer Zahl gibt an, wie viele Felder in dem Gebiet geschwärzt werden müssen. In Gebieten ohne Zahl können beliebig viele Felder geschwärzt werden.
• Die geschwärzten Felder dürfen keine gemeinsame Kante haben.
• Alle weißen Felder müssen innerhalb eines Gebiets miteinander verbunden sein (es ist möglich, dass ein Gebiet keine weißen Felder hat).
• Wenn zwei weiße Felder über eine Gebietsgrenze hinweg orthogonal nebeneinander liegen, bilden sie eine "Tür". Es kann nicht mehr als eine Tür zwischen zwei Gebieten geben.
• Alle weißen Felder müssen eine orthogonal zusammenhängende Fläche bilden.

Haisu ("Haus") ist ein von William Hu erfundenes Logikrätsel. Ein quadratisches oder rechteckiges Rastergitter ist in Regionen unterteilt. Ziel ist es, eine Linie ("Weg") von S (Start) nach G (Goal, Ziel) zu zeichnen, die durch alle Felder geht. Die Linie darf sich nicht selbst überqueren. Die Linie kann jede Region mehr als einmal besuchen. Wenn die Linie über ein Feld mit einer großen Zahl N verläuft, befindet sie sich an ihrem N-ten Eintritt in die Region. Wenn eine Region in der oberen linken Ecke eine kleine Zahl n hat, muss die Linie diese Region insgesamt n-mal besuchen.

Obitaru (aus dem Japanischen, wörtlich "Orbital") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein Rastergitter enthält weiße und schwarze Kreise; schwarze Kreise können Zahlen enthalten. Ziel ist es, quadratische oder rechteckige Schlaufen ("Gürtel") zu zeichnen. Die Schlaufen können sich kreuzen, parallele Linien können jedoch nicht durch dasselbe Feld verlaufen. Schlaufen müssen durch alle weißen Felder verlaufen. Es kann Schlaufen geben, die durch keinen weißen Kreis verlaufen. Ein schwarzer Kreis sollte sich innerhalb genau einer Schlaufe befinden (es darf nicht mehr als ein schwarzer Kreis innerhalb der Schlaufe sein). Wenn der schwarze Kreis eine Zahl enthält, ist diese gleich der Anzahl der weißen Kreise, durch die die Schlaufe um diesen schwarzen Kreis verläuft.

Square Jam ist ein Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern Zahlen. Ziel ist es, das Rastergitter in Quadrate zu unterteilen. Ein Feld mit einer Zahl gibt die Seitenlänge eines Quadrats an. Eine Quadrat kann eine beliebige Anzahl nummerierter Felder enthalten. Das Rastergitter kann Quadrate ohne Zahlen enthalten. In einem Rasterpunkt dürfen sich nicht die Ecken von vier Quadraten treffen.

Cocktail-Lampe ("Cocktail Lamp", "Kakuteruranpu") ist ein Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter wird in Regionen unterteilt. Das Ziel besteht darin, einige Felder des Rastergitters nach den folgenden Regeln zu schwärzen:

• Alle schwarzen Felder einer Region müssen horizontal oder vertikal verbunden sein (sie bilden einen "Block").
• Ein Feld mit einer Zahl gibt an, wie viele Felder in der Region geschwärzt werden müssen.
• In einer Region ohne Zahl können beliebig viele Felder geschwärzt werden (alle Felder können weiß bleiben).
• Wenn zwei Felder über eine Regionsgrenze hinweg orthogonal benachbart sind, muss mindestens ein Feld weiß sein.
• Alle Blöcke aus schwarzen Feldern müssen durch ihre Ecken miteinander verbunden sein.
• Kein 2 x 2-Felderbereich innerhalb des Rastergitters darf nur schwarze Felder enthalten.

Kazoku ("Kazoku shashin"; aus dem Japanischen, wörtlich "Familienfoto") ist ein Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter enthält in einigen Feldern schwarze Kreise; einige Kreise können Zahlen oder Fragezeichen enthalten. Außerdem können einige Felder Zahlen oder Fragezeichen enthalten. Ziel ist es, das Rastergitter in Rechtecke zu unterteilen, sodass jedes Rechteck genau eine Zahl oder ein Fragezeichen enthält. Eine Zahl gibt an, wie viele schwarze Kreise das Rechteck enthält. Ein Rechteck mit einem Fragezeichen kann beliebig viele schwarze Kreise enthalten (mindestens einen). Orthogonal benachbarte Kreise müssen zum gleichen Rechteck gehören.

Tontonbeya (aus dem Japanischen wörtlich "Zocker") ist ein von Nikoli veröffentlichtes Logikrätsel. Ein rechteckiges oder quadratisches Rastergitter wird in Gebiete unterteilt. Das Ziel besteht darin, jedes Feld mit Figuren zu füllen: Quadrate, Kreise, Dreiecke. Ein Gebiet kann beliebige Figurentypen enthalten, wenn es sich jedoch um unterschiedliche Figurentypen handelt, sollte die Anzahl der Figuren jeder Art gleich sein. Alle Figuren des gleichen Typs in einem Gebiet müssen horizontal oder vertikal verbunden sein (sie bilden einen "Block"). Jeder Block mit denselben Figuren innerhalb eines Gebiets muss an einen Block mit denselben Figuren in einem anderen Gebiet angrenzen. Es sollte keinen Block geben, der an zwei oder mehr Blöcke derselben Figur in anderen Gebieten angrenzt.

Kontext ("Context") ist ein rechteckiges oder quadratisches Rastergitter mit Zahlen in einigen Feldern. Ziel ist es, Felder des Rastergitters nach folgenden Regeln zu schwärzen:

• Alle weißen Felder müssen horizontal oder vertikal verbunden sein.
• Ein Feld mit einer Zahl kann geschwärzt werden. Je zwei schwarze Felder dürfen nicht orthogonal benachbart sein.
• Die Zahl in einem weißen Feld gibt die Anzahl der orthogonal benachbarten schwarzen Felder an.
• Die Zahl in einem schwarzen Feld gibt die Anzahl der diagonal angrenzenden schwarzen Felder an.

Wortsuche (auch bekannt als "Word Finder", "Word Search", "Word Seek", "Word Sleuth", "Mystery Word") besteht aus einem Rastergitter mit Buchstaben. Ziel dieses Puzzles ist es, alle Wörter, die in diesem Rastergitter versteckt sind, zu finden und zu markieren. Die Buchstaben in jedem Wort sind orthogonal zusammenhängend. Jeder Buchstabe kann nur zu einem Wort gehören.

Eine Wortliste soll für das Erstellen des Puzzles benutzt werden. Auch das Schlüsselwort kann angegeben werden; dieses Wort wird von den übrigen Buchstaben im Rastergitter gebildet.

Neun Buchstaben ("Nine Letters") ist eine Variation des Wortsuche-Puzzles. Das Puzzle besteht aus einem Rastergitter mit Buchstaben. Das Rastergitter ist unterteilt in 3 x 3 Untergitter. Das Ziel ist, verborgene Wörter innerhalb jedes Untergitters zu finden und zu markieren.

Spinnennetz ("Spider Web") besteht aus Kreisen, die mit Linien verbunden sind. Jeder Kreis enthält einen Buchstaben. Ziel ist es, ein Schlüsselwort zu finden, das im Netz der Kreise verborgen ist, und dieses zu markieren.

Irrgarten ("Maze") ist ein Puzzle, das aus einem komplizierten Netz von Wegen besteht. Das Ziel ist, einen Pfad zwischen zwei ausgewählten Punkten zu finden. Das Programm ermöglicht es, Puzzles mit rechteckiger, quadratischer oder unregelmäßiger Form zu erstellen.