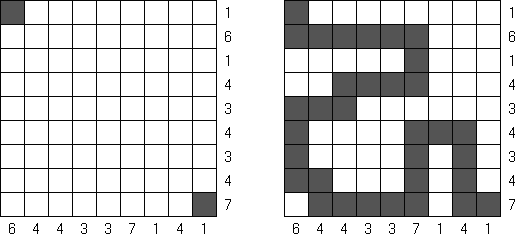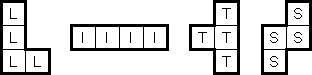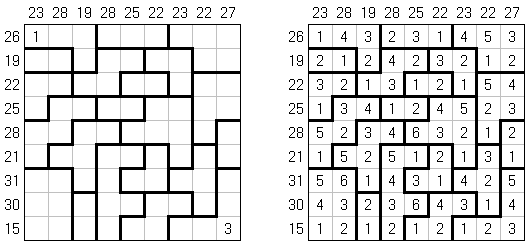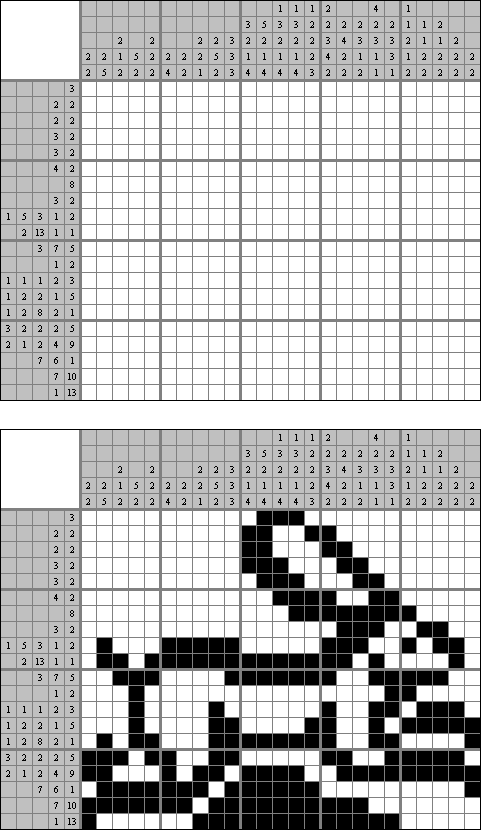
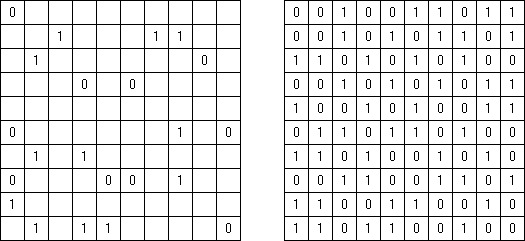
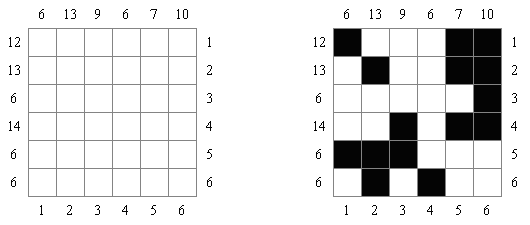
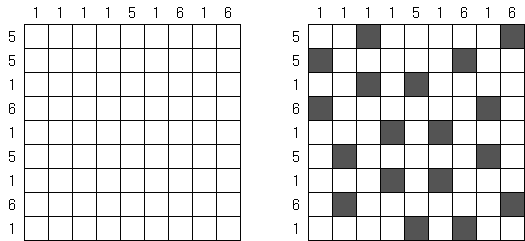
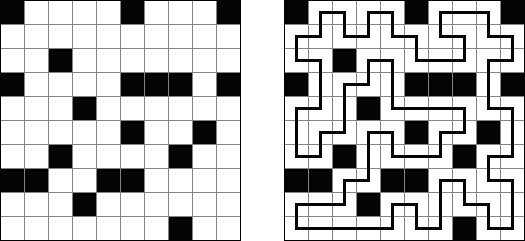
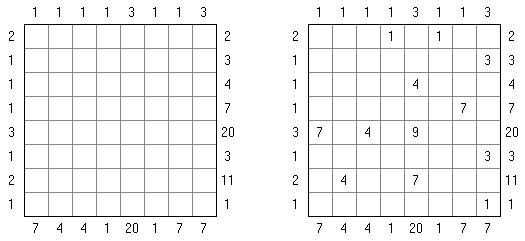
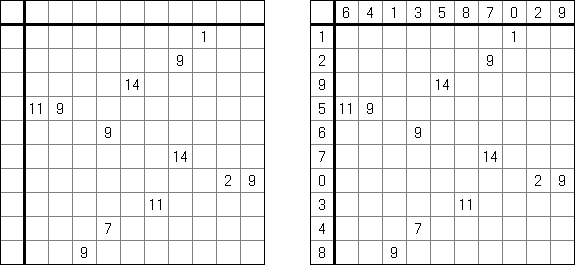
Cross+A Logiikkapelit

Cross+A ratkaisee ja tekee monta erilaista logiikkapelia. Laaditun logiikkapelin voit tallentaa kuvatiedostoksi (seuraavat muodot sallittu: BMP, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF, Windows-metatiedostot sekä CorelDRAW-tiedostot). Logiikkapelit voidaan laatia myös paketeittain.

Japanilainen ristikko (tunnetaan myös nimellä "Nonogram", "Hanjie", "Paint By Numbers", "Griddler", "CrossPix") on ristikkotyyppi, jossa on tarkoituksena värittää ristikon ruuduista vihjeiden avulla ruutuja. Värtetyistä ruuduista muodostuu kuva. Ruuturivien ylä- ja sivumarginaaleissa kerrotaan vihjeenä kunkin rivin peräkkäisten väritettävien ruutujen määrä. Väritettyjen ruuturyhmien väliin on aina jätettävä vähintään yksi tyhjä ruutu.

Cross+A pystyy ratkaisemaan sekä mustavalkoisia, että monivärisiä japanilaisia ristikkoja. Käyttäjä syöttää ruudukon koot ja sitten pilkuilla toisistaan erotettuja lukuja, jotka määräävät peräkkäisten väritettävien ruutujen määrän ylä- ja sivumarginaaleissa.

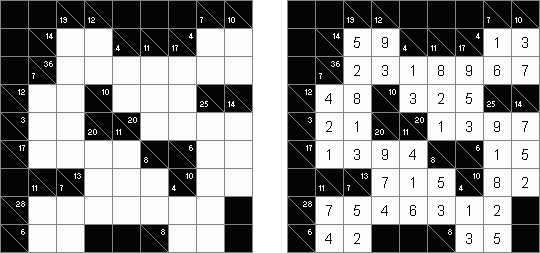
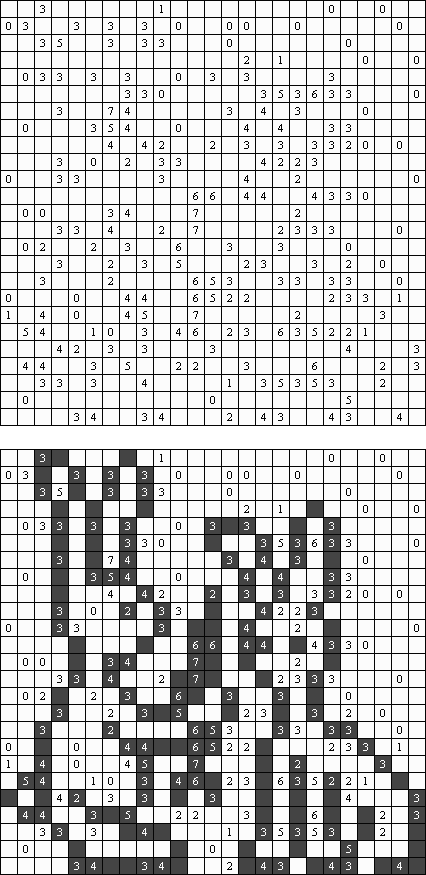
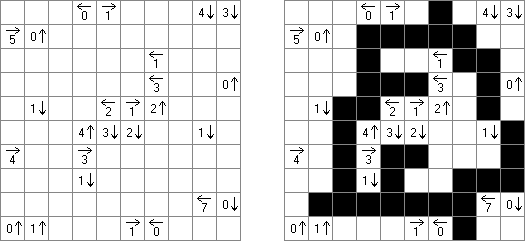
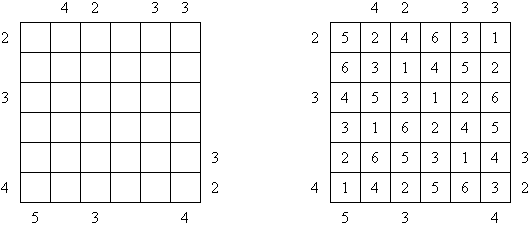
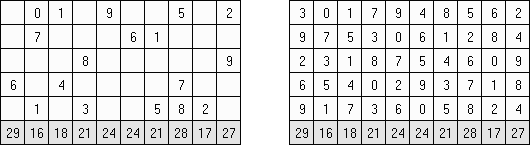
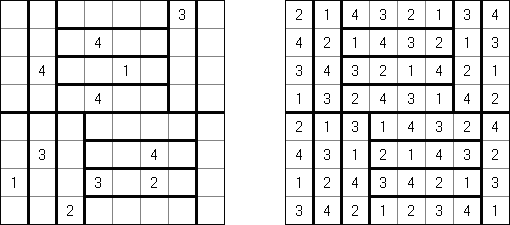
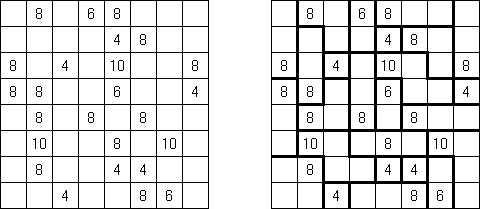
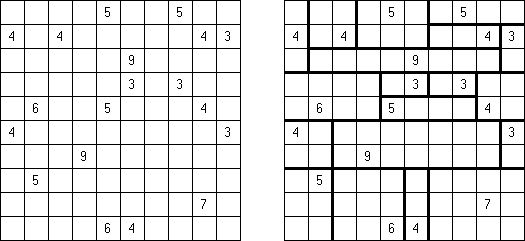
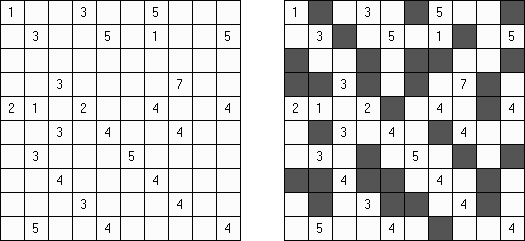
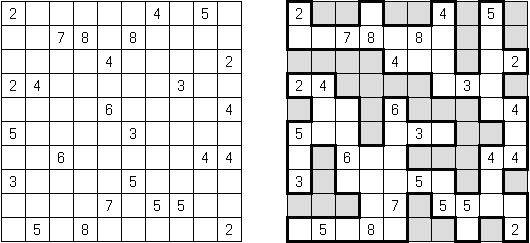
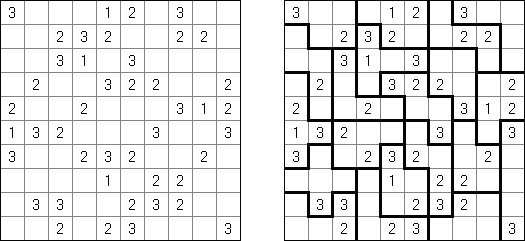
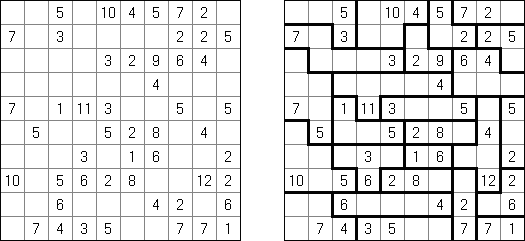
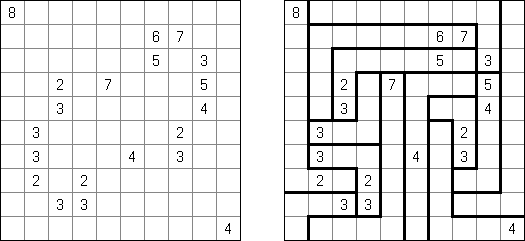
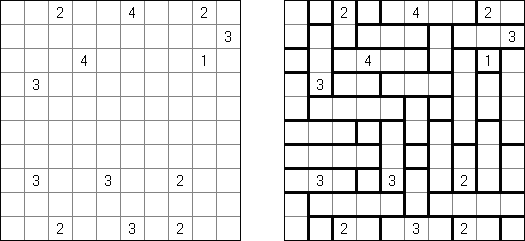
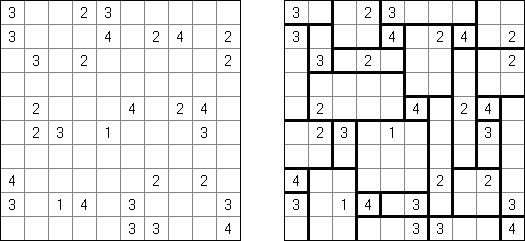
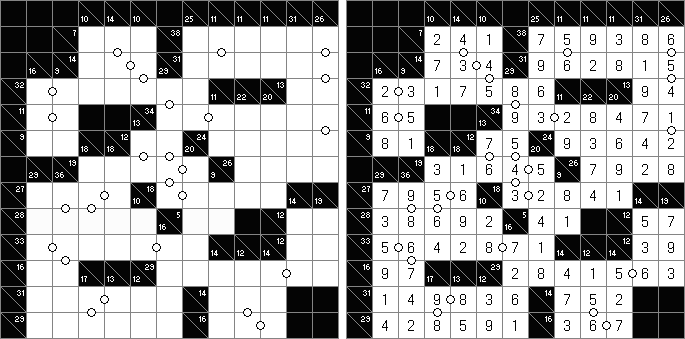
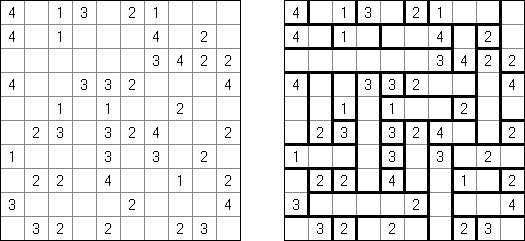
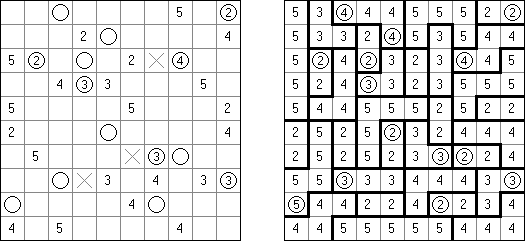
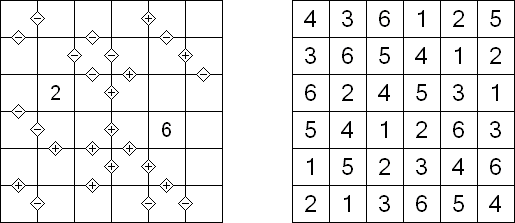
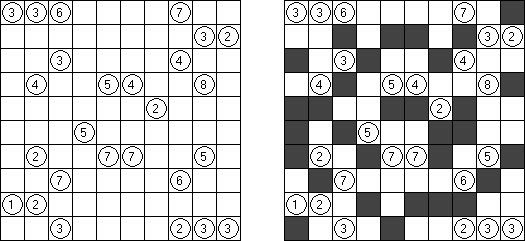
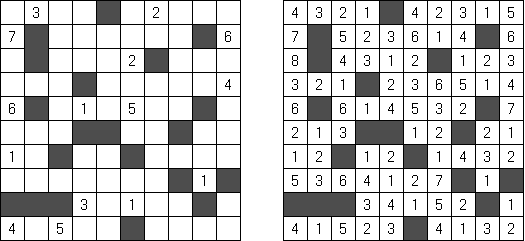
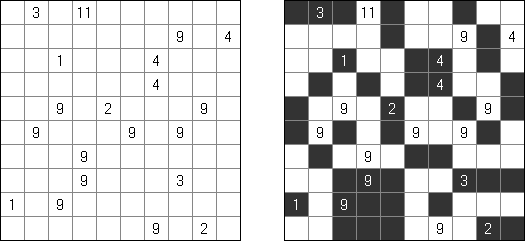
Kakuro ("Cross Sums") on sanakistikkoa vastaava numeropeli. Peli koostuu tavallisimmin nelikulmaisesta ruudukosta, mutta pelistä on myös huomattavasti suurempia versioita. Ruudukossa on tyhjiä ruutuja, joihin täytetään numeroita vaaka- ja pystysuoraan käyttäen numeroita 1-9 siten, että ruudukon toisiinsa risteävällä pysty- ja vaakarivillä sama numero saa esiintyä vain kerran. Tarkoituksena on saada vaakarivin tyhjiin ruutuihin luvuista 1-9 sen vasemmalla puolella mainitun luvun summa ja vastaavasti pystyruudukoissa yläpuolella mainittu luku. Esimerkiksi luku 6 voidaan esittää lukujen 1 ja 5 tai 2 ja 4 summana, samojen lukujen käyttö (esim. 3 ja 3) on kielletty.

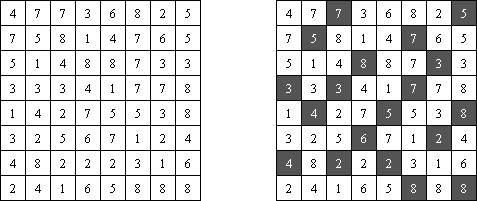
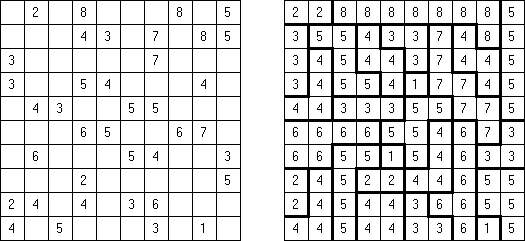
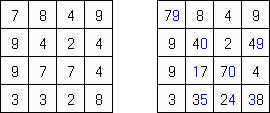
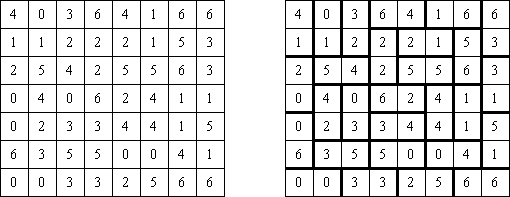
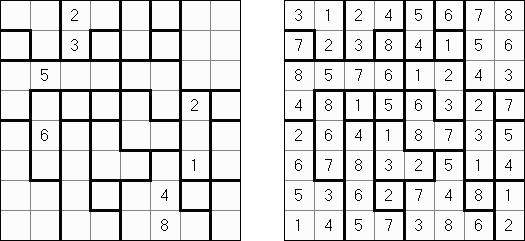
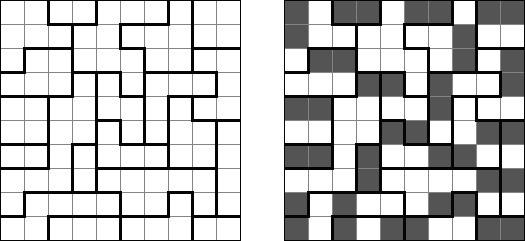
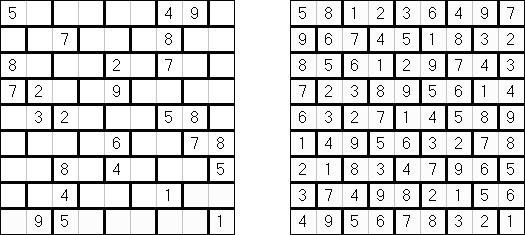
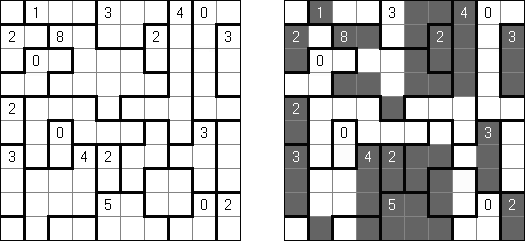
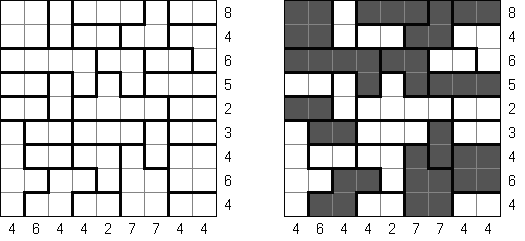
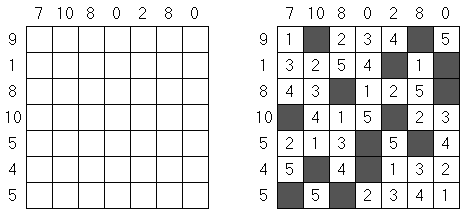
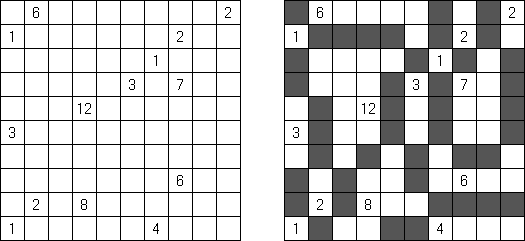
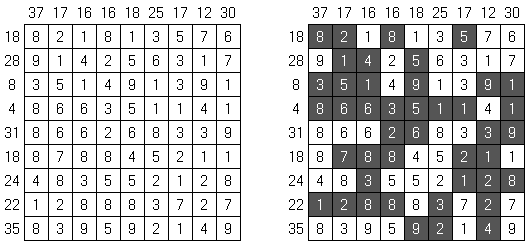
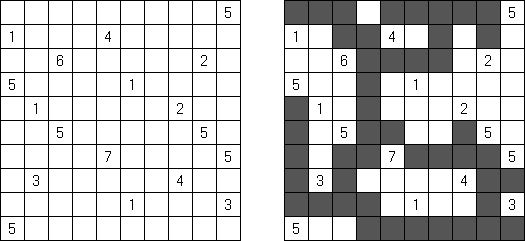
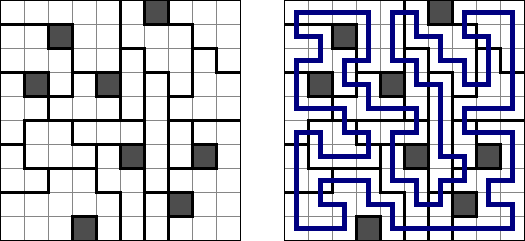
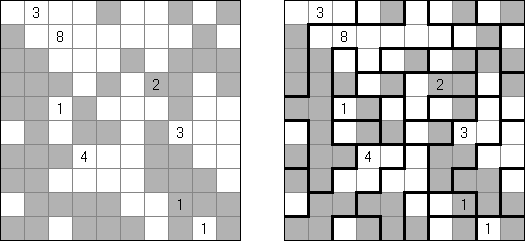
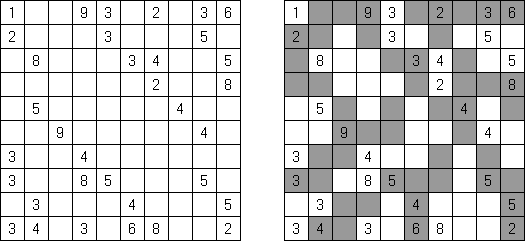
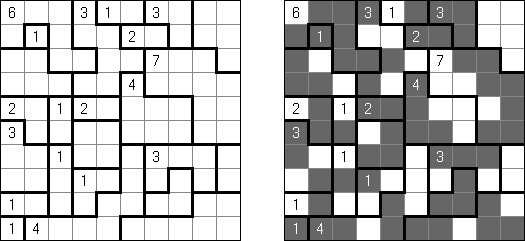
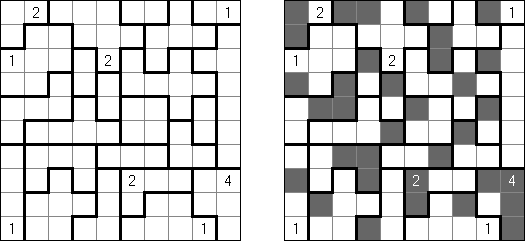
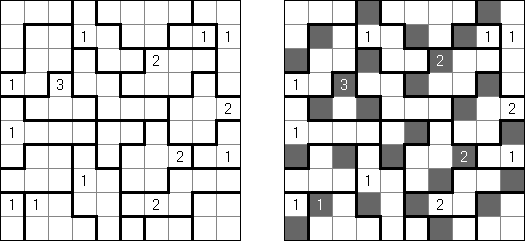
Hitori-ruudukko on neliö, jonka ruudut on täytetty luvuilla. Tehtävänä on poistaa lukuja niin, että mikään luku ei esiinny vaaka-eikä pystyrivissä kuin korkeintaan kerran. Lisäksi poistetut ruudut eivät saa koskettaa toisiaan vaaka-tai pystysuorassa suunnassa ja valkoisiksi jätettyjen ruutujen täytyy muodostaa yksi yhtenäinen alue.

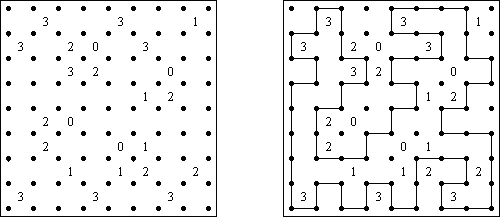
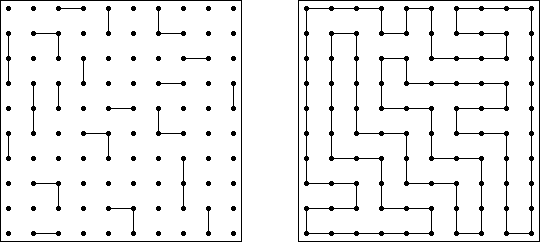
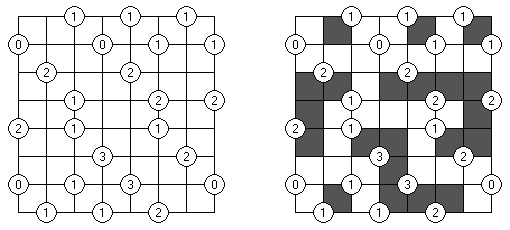
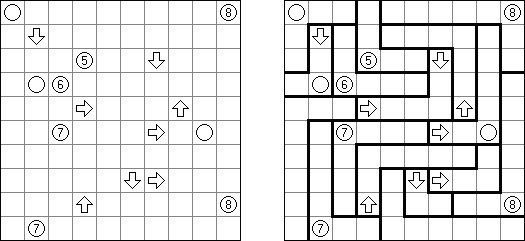
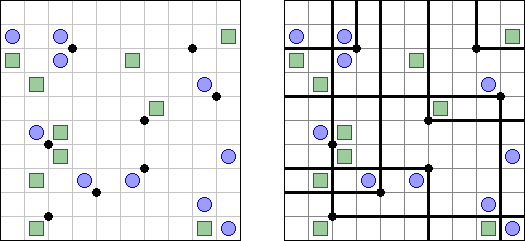
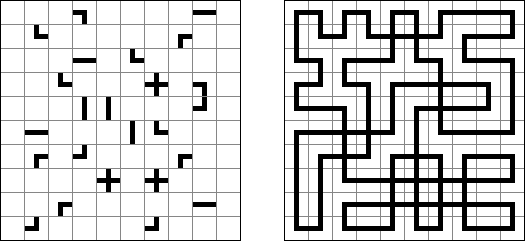
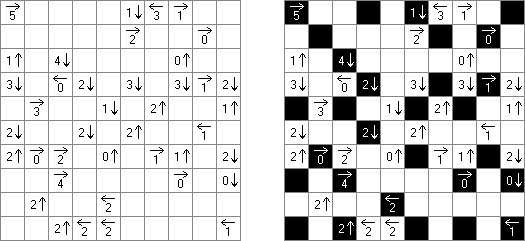
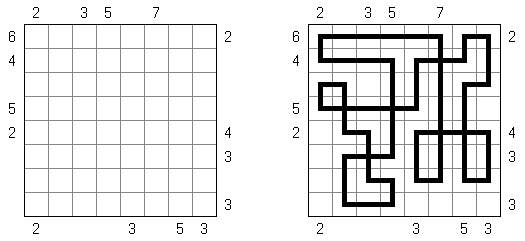
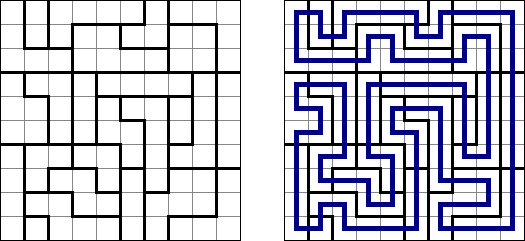
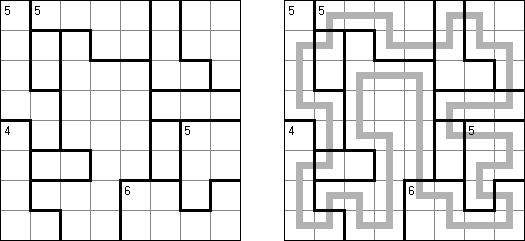
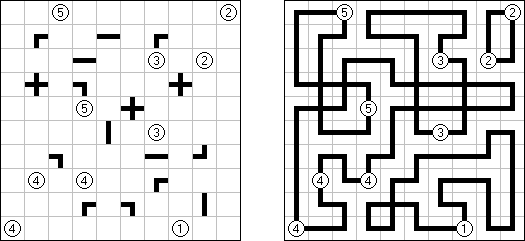
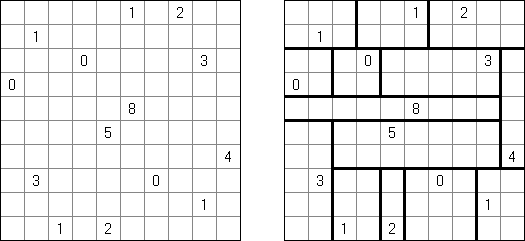
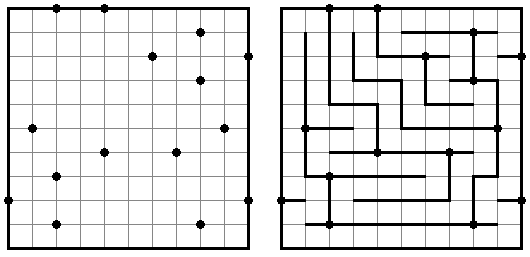
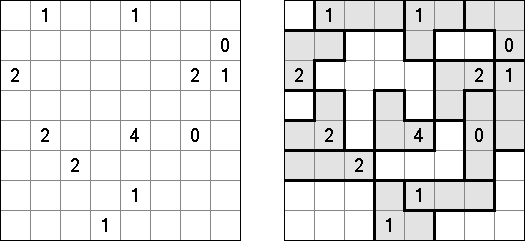
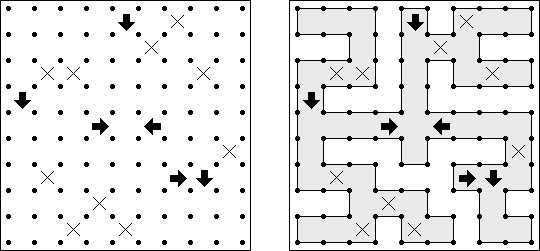
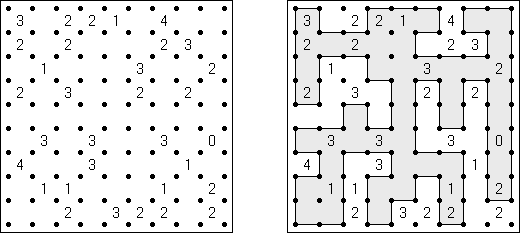
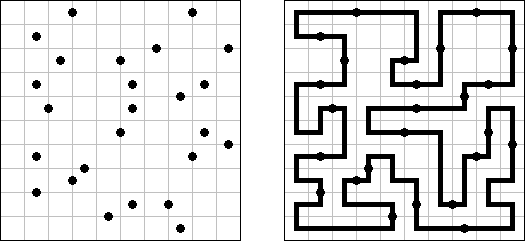
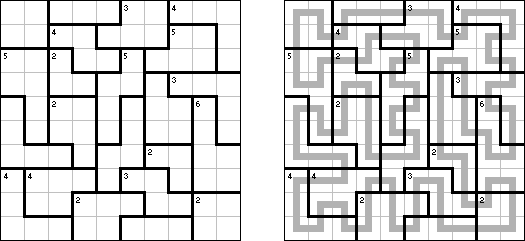
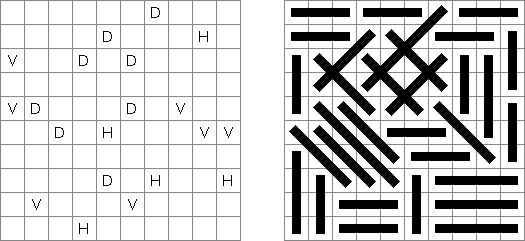
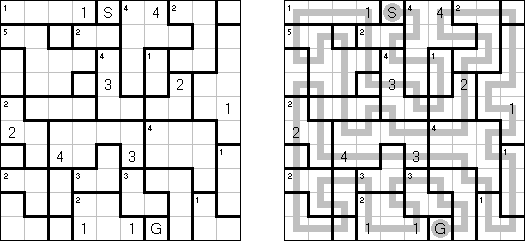
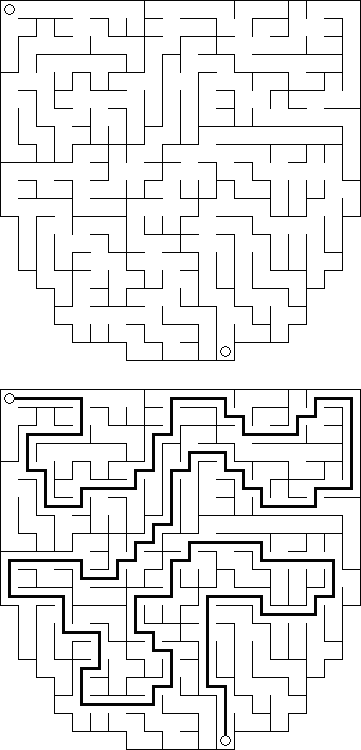
Slitherlink ("Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin", "Great Wall of China") on sokkelon näköinen logiikkapeli. Ristikko koostuu suorakulmion muotoisesta pisteistöstä, jonne on sijoitettu muutamia vihjeitä. Tarkoituksena on yhdistää pisteet niin, että jokaisen vihjeen ympäri kulkee viivoja vihjeen ilmoittama määrä. Kaikki viivat muodostavat yhtenäisen ketjun, jossa ei ole risteyksiä eikä haaroja. Tyhjien ruutujen ympäri voi kulkea viivoja miten monta tahansa.

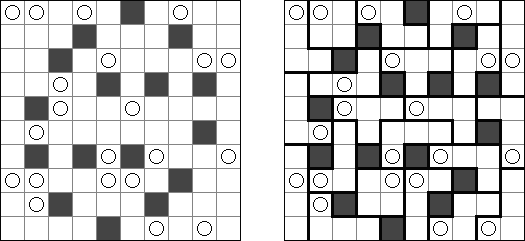
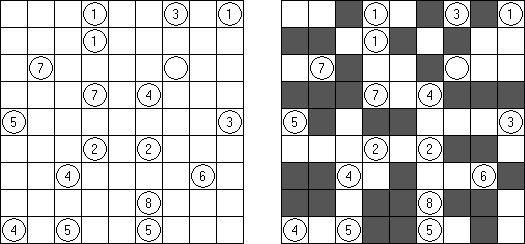
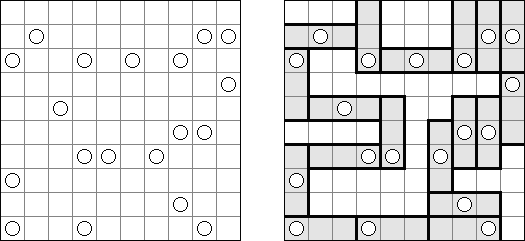
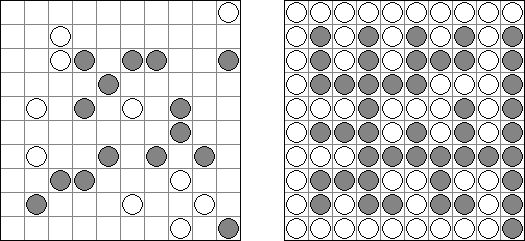
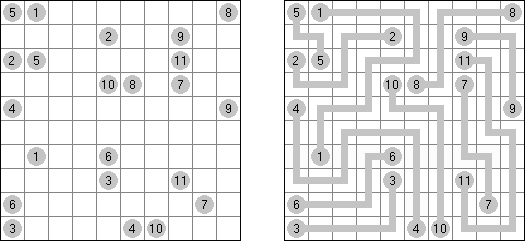
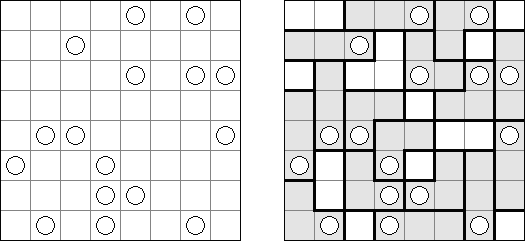
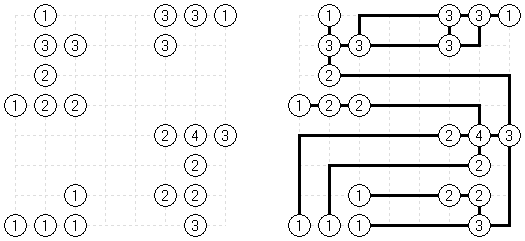
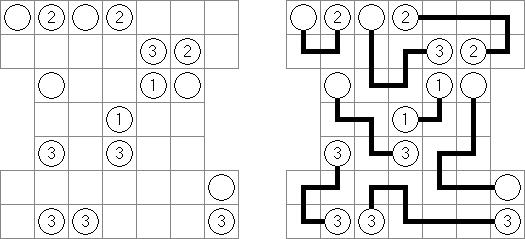
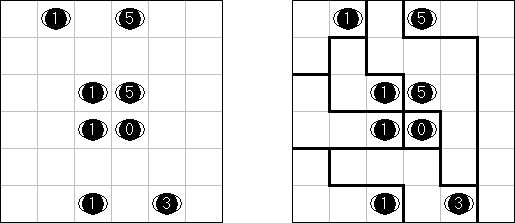
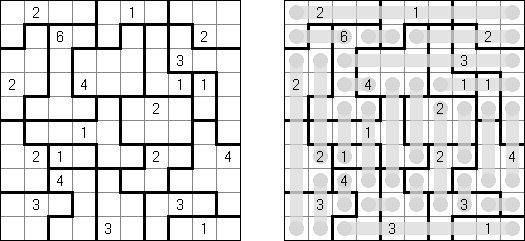
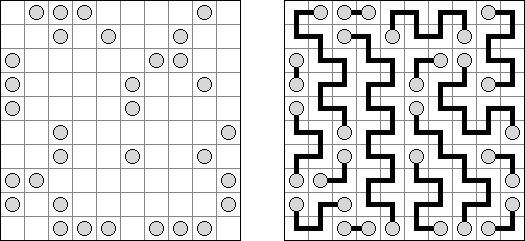
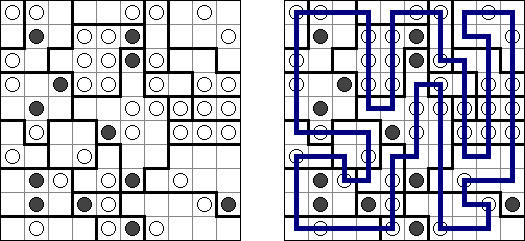
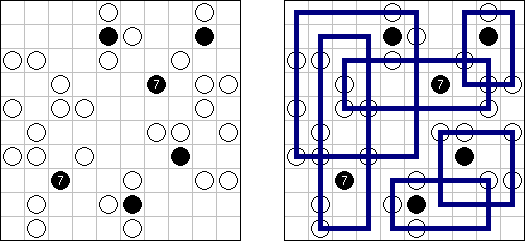
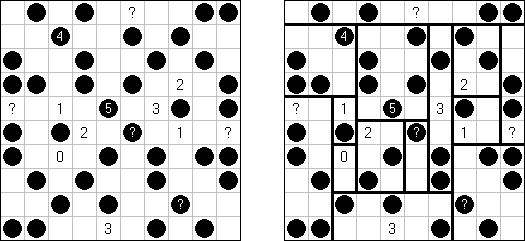
Link-a-Pix ("Paint by Pairs") koostuu ristikosta, jossa vinkit ovat lukuja sijoitettuna ristikkoon satunnaiselta näyttäviin paikkoihin. Jokainen vinkki paitsi 1 on puolikas parista. Tavoitteena on paljastaa ristikkoon piilotettu kuva yhdistämällä oikeat parit. Yhdistäminen tehdään polulla, jonka pituus on sama kuin molemmissa päissä oleva luku, ja päät lasketaan mukaan pituuteen. Ruudut, joissa on 1, edustavat polua, jonka pituus on 1. Polut voivat kulkea pysty- ja vaakasuoraan (ei hyppyjä kulmittain) ja kaksi polkua eivät saa kulkea ristiin toistensa kanssa.

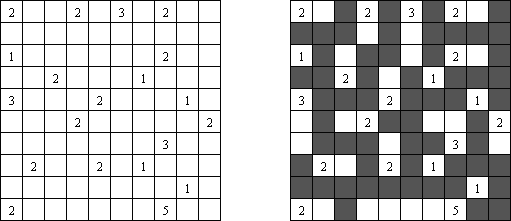
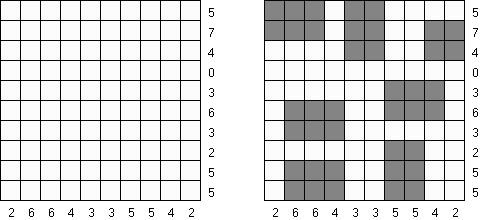
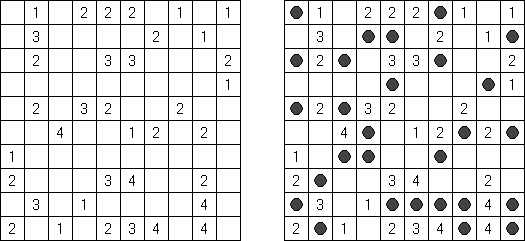
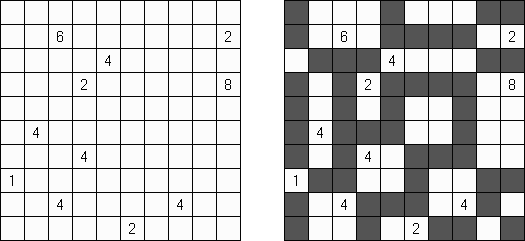
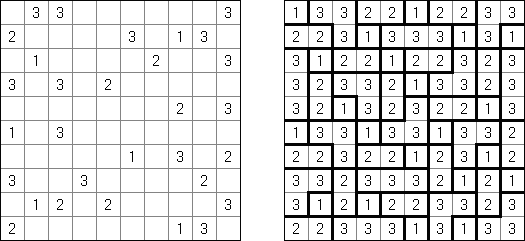
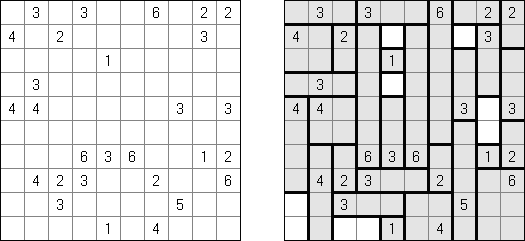
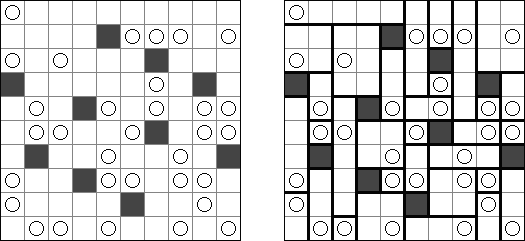
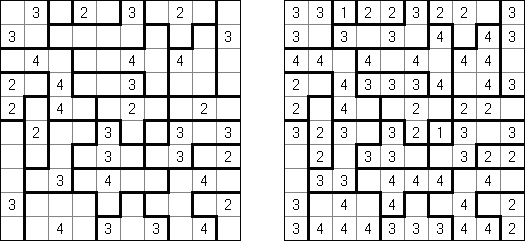
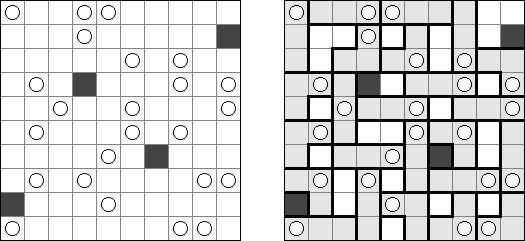
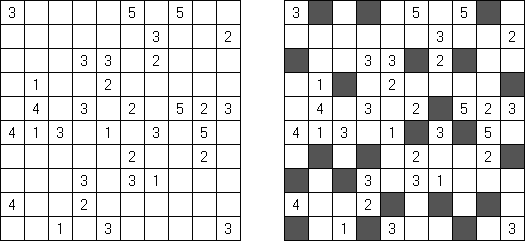
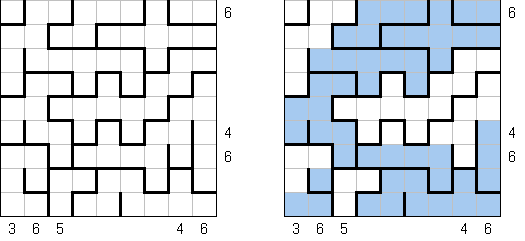
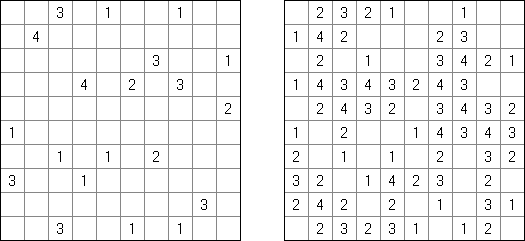
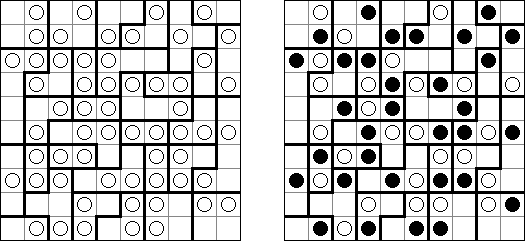
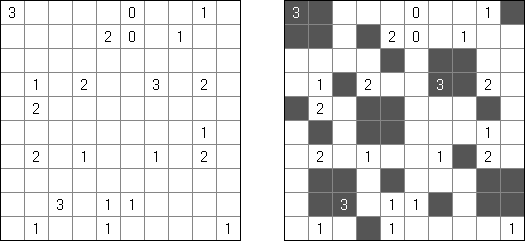
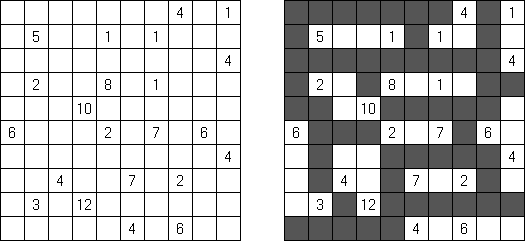
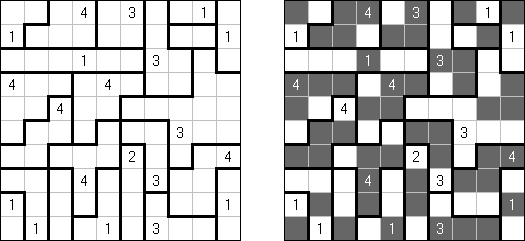
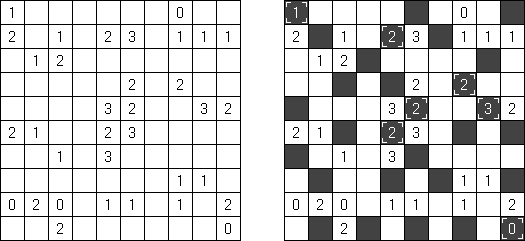
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") on ristikko, jossa kuva on koodittu luvuilla. Jokaisessa ristikossa on ruudukko, jossa on viheitä eri paikoissa. Tehtävänä on paljastaa piilotettu kuva niin, että väritettyjen ruutujen lukumäärä vihjeen ympärillä, ruutu itse mukaan luettuna on sama kuin ruudussa annettu vihje.

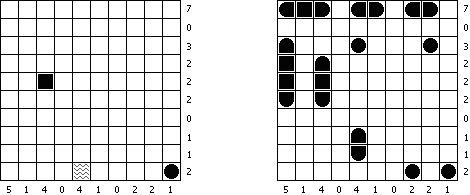
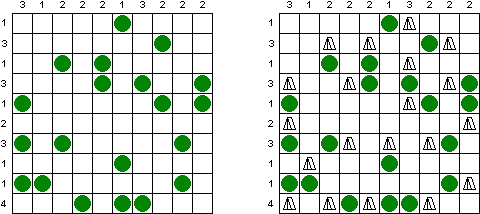
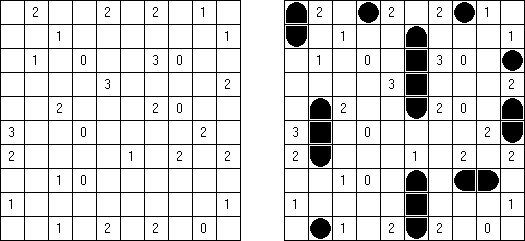
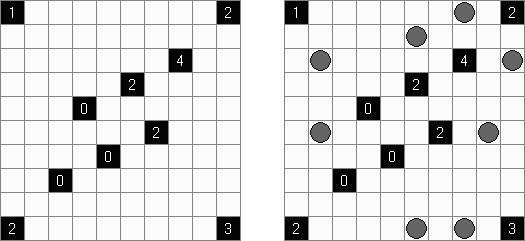
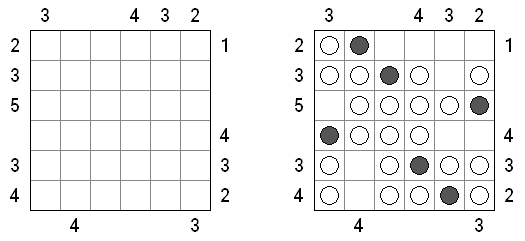
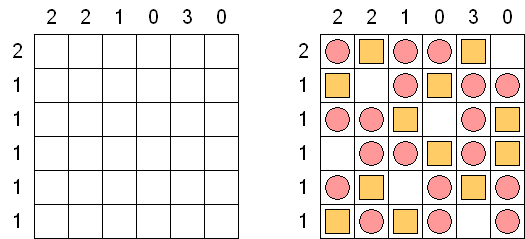
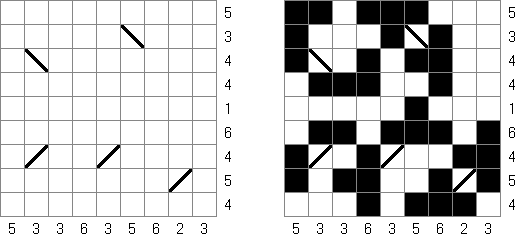
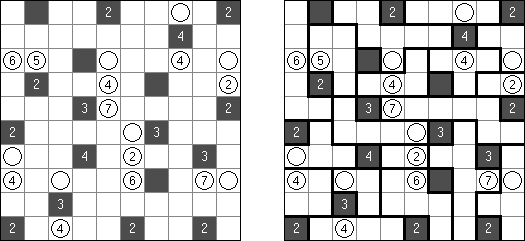
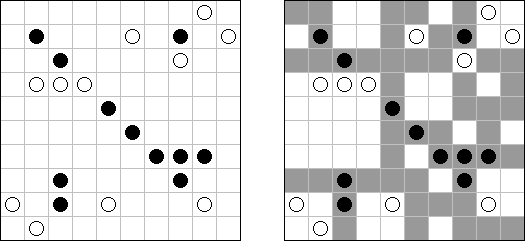
Battleships ("Solitaire Battleships", "Battleship Solitaire") on logiikkapeli, jonka säännöt ovat lähes samanlaisia kuin saman nimisen pelin. Laivot tulee sijoittaa siten, jotta ne eivät koske toisiaan. Sivu- ja alamarginaaleissa olevat luvut kertovat kuinka monta laivojen osaa on kyseisessä pysty- tai vaakasuora rivissä.

Klassikkopeli ruudukon koot ovat 10 x 10. Olemassa on yksi neljäruutuinen laiva, kaksi kolmeruutuista, kolme kaksiruutuista ja neljä yhdenruutuista. Joskus tiedyt laivan osat on jo merkitty ruudukkoon.

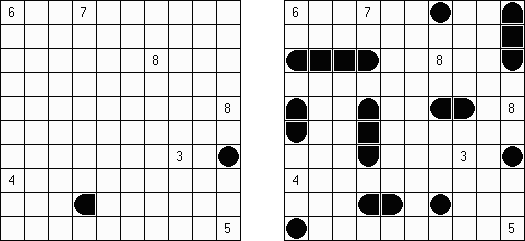
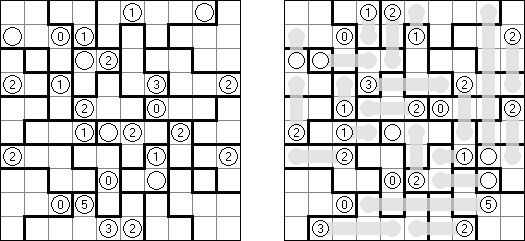
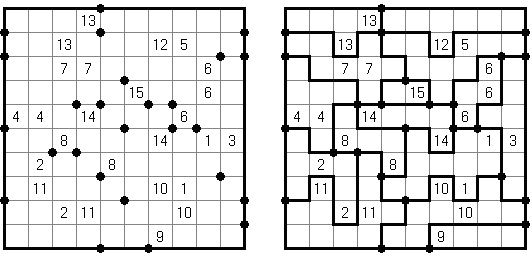
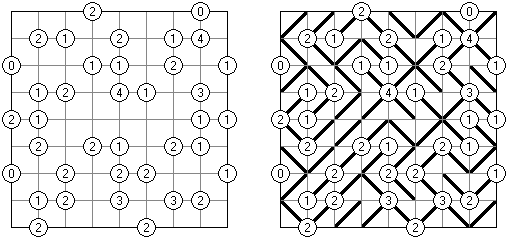
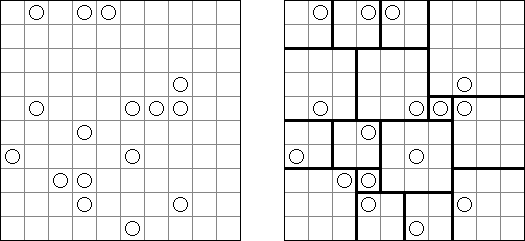
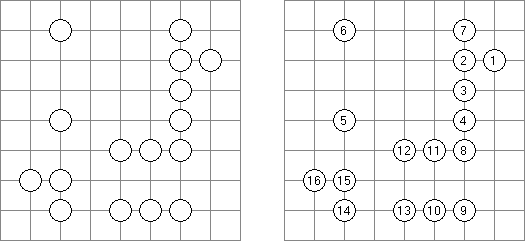
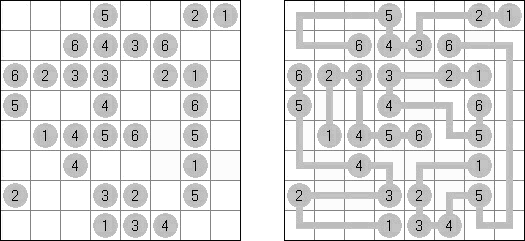
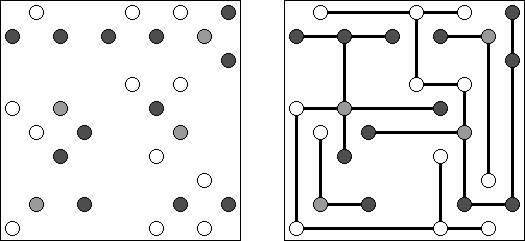
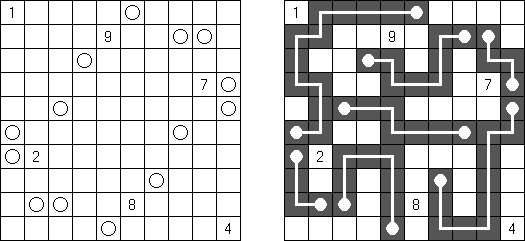
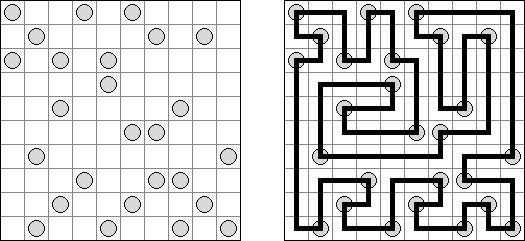
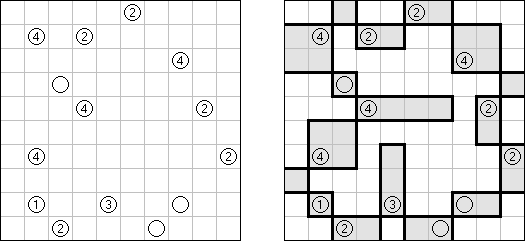
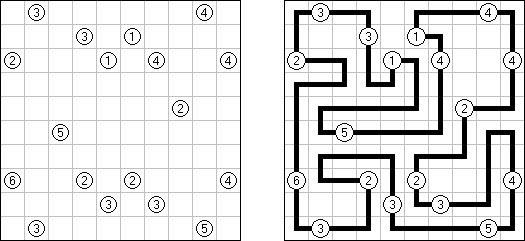
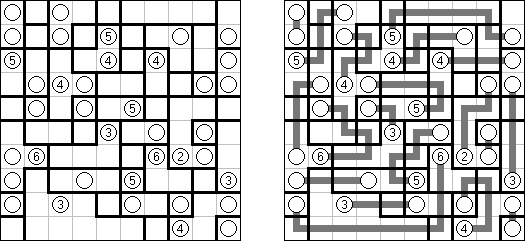
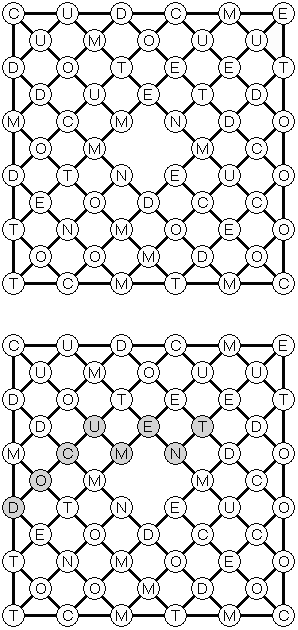
Hashiwokakero ("Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai"). Ristikko koostuu suorakulmion muotoisesta alueesta, jossa on numeroin varustettuja ympyröitä. Jokainen ympyrä edustaa saarta ja numero on saareen littyvien siltojen lukumäärä. Tehtävänä on yhdistää kaikki saaret siten, että korkeintaan kaksi siltaa on kahden saaren välissä ja kaikki saaret on yhdistetty toisiinsa. Jokaisesta saaresta on siis oltava polku jokaiseen muuhun saareen. Sillat voivat kulkea vain vaaka- tai pystysuoraan ja sillat eivät saa leikata toisiaan, eikä muita saaria.

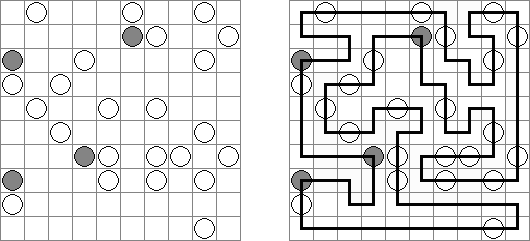
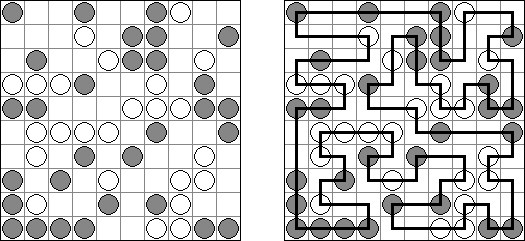
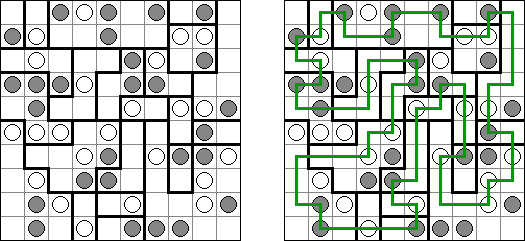
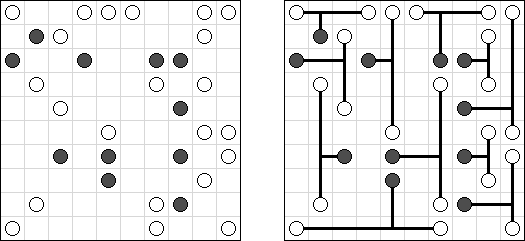
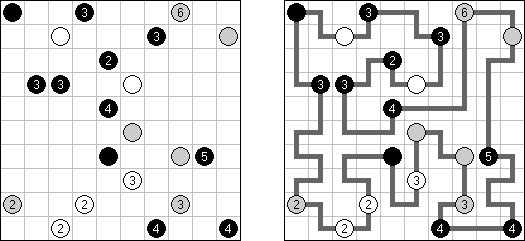
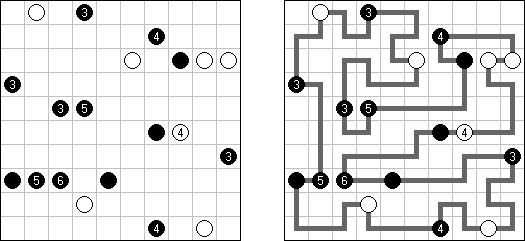
Masyu ("Shiroshinju Kuroshinju", "White Pearls and Black Pearls"). Tarkoituksena on yhdistää mustat ja valkoiset ympyrät niin, että kaikki viivat muodostavat yhtenäisen ketjun, jossa ei ole risteyksiä eikä haaroja. Valkoiset ympyrät yhdistetään suoralla viivalla, joka eteisessä tai seuraavassa ruudussa (tai molemmissa) kääntyy sivulle. Kun viiva ylittää mustan ympyrän se kiertyy 90 asteen kulmaan, samalla sekä eteisessä, että seuraavassa ruudussa viiva menee suoraan.

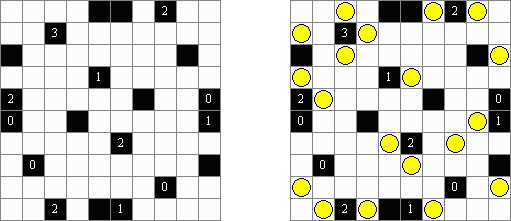
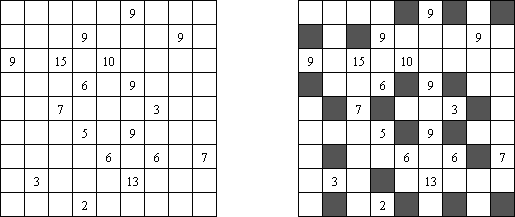
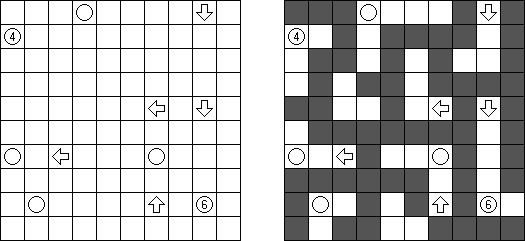
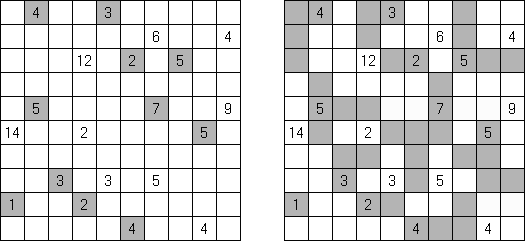
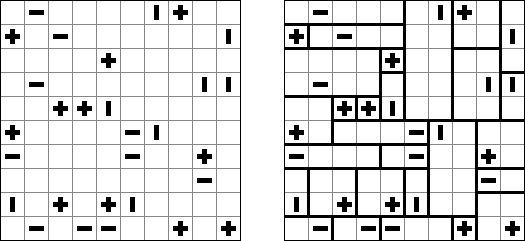
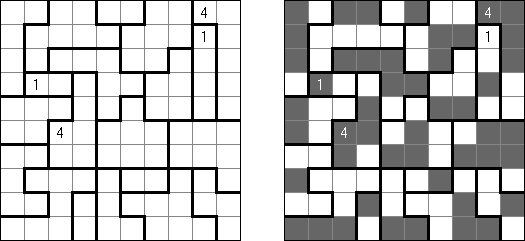
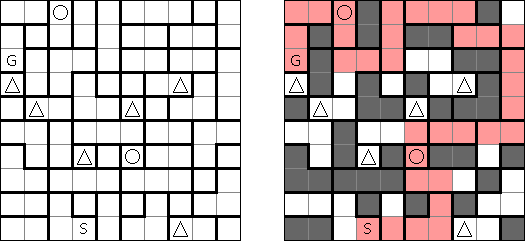
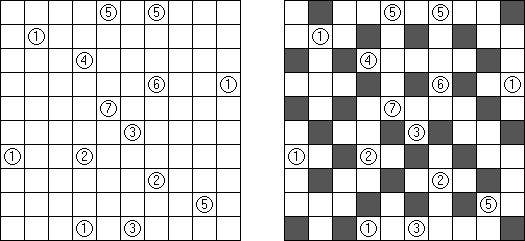
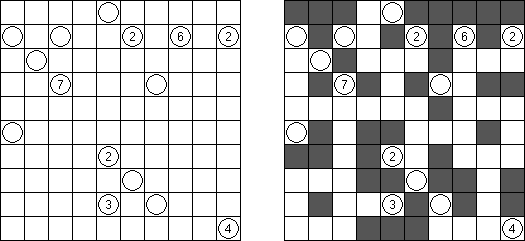
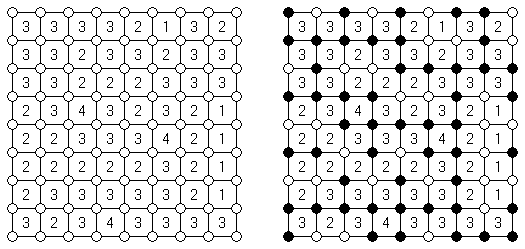
Akari ("Light Up", "Bijutsukan") ristikko koostuu mustista ja valkoisita ruuduista, joissakin mustissa ruuduissa on lukuja. Tarkoituksena on sijoittaa valkoisiin ruutuihin ns valaisimet siten, että koko ristikko on valaistu ja samalla valaisimet eivät valaise toisiaan.

Valaisimen valo leviää vaaka- ja pystysuoraan, mutta sitä estävät mustat ruudut. Mustassa ruudussa oleva 0-4 luku kertoo kuinka monta valaisinta tulee sijoita sen vieressä vinottain olevia valaisimia lukuun ottamatta. Tyhjien ruutujn ympäri voi olla valoisimia miten monta tahansa.

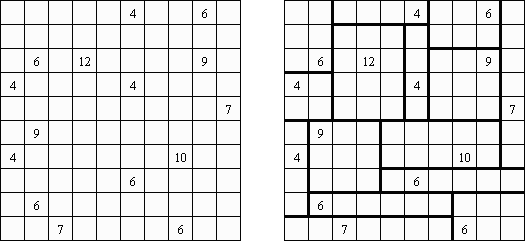
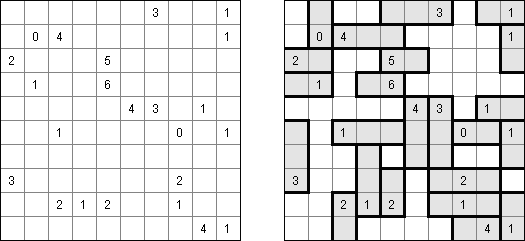
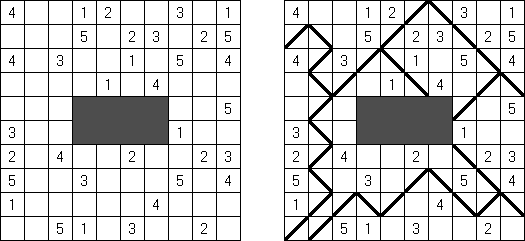
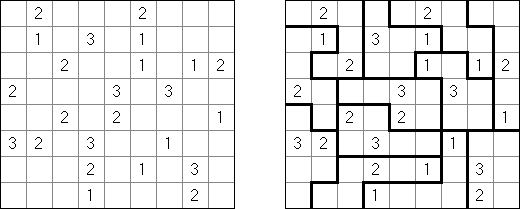
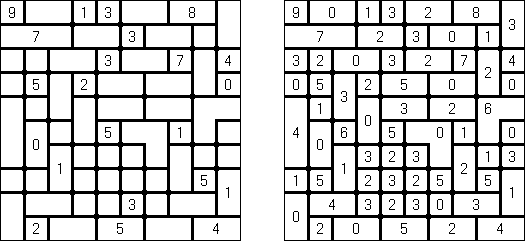
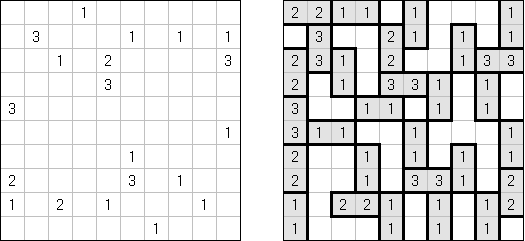
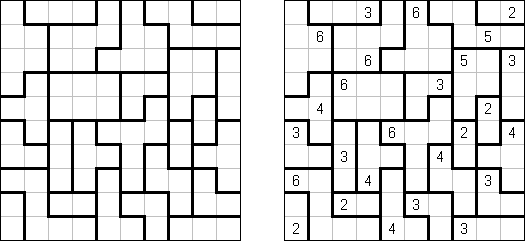
Fillomino ("Polyominous") - ristikko koostuu suorakulmaisesta ruudukosta, jonka tiettyihin ruutuihin sisältyy lukuja. Tehtävänä on jakaa ruudukon muutamiin osiin, joista kussakin olevien ruutujen määrästä kertoo osan luku. Samankokoiset osat eivät saa koskea toisiinsa. Tyhjät ruudut voidaan yhdistää pelin ratkaisemiseksi tarvittaviin osiin.

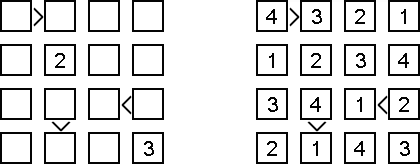
Futoshiki ("Hutoshiki", "Unequal") ristikko koostuu nelikulmaisesta ruudukosta, jonka tietyt ruudut sisältävät lukuja. Ruutujen välillä joskus on mekki "<" tai ">", jotka kertovat viereisten lukujen valisestä suhteisesta. Taroituksena on täyttää tyhjät ruudut siten, että jokaisessa pysty- ja vaakasuora rivissä on vain yksi sama luku.

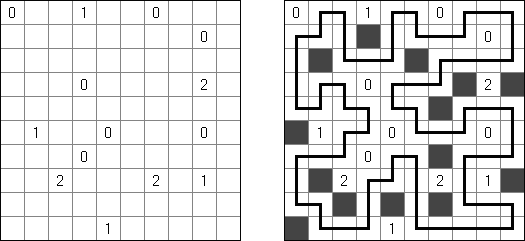
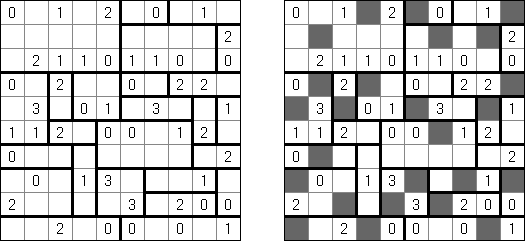
Kuromasu ("Kurodoko", "Where is Black Cells?") ristikko koostuu nelikulmaisesta ruudukosta, jonka tietyt ruudut sisältävät lukuja. Pelaaja värittää ruutuja noudattaen seuraavia sääntöjä:

• Luku määrää kuinka monta valkoista ruutua "näkyy" kyseisestä ruudusta pysty- ja vaakasuoraan. "Näkö" yltää ruudukon rajaa taikka musta ruutua.
• Lukuruudut ovat aina valkoisia.
• Mustat ruudut eivät voi koskea toisiinsa vaaka-tai pystysuoraan.
• Kaikki valkoiset ruudut muodostuvat yhtenäisen valkoisen pinnan, eli ne koskevat toisiinsa vaaka-tai pystysuoraan.

Nurikabe ("Cell Structure", "Islands in the Stream") on japanilainen looginen ruudunpäättelypeli. Nurikabe on japania ja japanin kansantaruissa se viittaa tietä tukkivaan näkymättömään seinään, johon jalkaisin kulkevat vetoavat myöhästyessään.

• Valkoiset ruudut muodostavat "saaria", kaksi saarta saavat koskea toisiinsa vain kulmilla.
• Jokaisen saaren ruutujen määrästä kertoo itse saareen sisältyvä numeroitu ruutu.
• Jokaisessa saaressa saa olla vain yksi numeroitu ruutu ja.
• Kaarien välissä ruudut muodostavat "virran".
• Kaikkien mustien ruutujen täytyy muodostaa yhtenäinen ketju.
• Kaikkien mustien ruutujen täytyy muodostaa yhtenäinen ketju, joka ei sisällä 2 x 2 ruutua suurempia mustien palikoiden keskittymiä.

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

Tents ("Tents and Trees") on ristikko, jonka tiedyt ruudut sisältävät "puita". Tarkoituksena on sijoittaa puiden viereen "telttoja" noudattaen suraavia sääntöjä:

• Telttojen määrä on sama kuin puiden.
• Jokainen teltta sijoittuu "oman" puun viereen vaaka- tai pystysuoraan, ei kuitenkaan vinottain. Jos tämä ehto on toteutunut, "vieraan" puiden sijoituksella ei ole merkitystä.
• Kaksi telttaa ei voi sijoittua vierekkäisiin ruutuihin mm vinoittain.
• Ylä- ja sivumarginaaleissa olevat luvut kertovat kyseisen vaaka- tai pystysuoran rivin telttojen lukumäärästä.

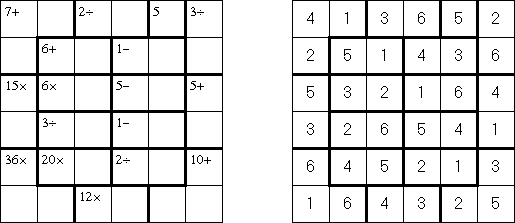
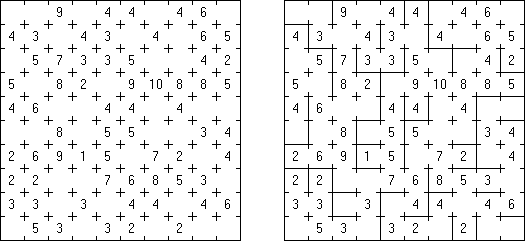
Calcudoku ("KenKen", "KENKEN", "KenDoku", "Square Wisdom") ratkaistaan lisäämällä ristikkoon numerot yhdestä numeroon N (N on rivien ja sarakkeiden lukumäärä) niin, että kukin numero esiintyy täsmälleen kerran jokaisella rivillä ja jokaisessa sarakkeessa. Lisäksi jokaisessa laatikossa olevat numerot antavat vastaukseksi laatikon yläkulmassa olevan luvun, kun sovelletaan yläkulmassa mainittua operaatiota. Operaationa voi olla yhteen-, vähennys-, kerto- ja jakolasku. Vähennyslaskussa suuremmasta aina vähennetään pienempi, eikä paikalla ristikossa sinänsä ole väliä.

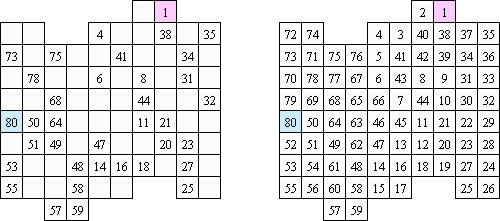
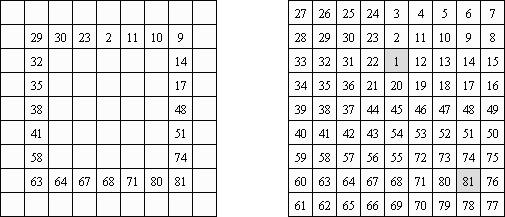
Hidato (jiddi: "minun peli"; tunnettu myös nimellä "Hidoku") on israelilainen matematiikko Gyora Benedekin keksintö. Ruudukon muoto saa olla mikä tahansa, yleensä se on kuitenkin suorakulmio tai neliö, johon sisältyy ruutuja. Tarkoituksena on täyttää kaikki ruudut johdonmukaisilla luvuilla, jotka liittyvät toisiinsa vaaka- tai pystysuoraan tai vinottain. Jokaisen pelin ruudukkoon on jo lisätty pienin ja suurin luku. Myös ruudukko saattaa sisältää muutkin luvut, jotka helpottavat ratkaisemista ja takaavat ratkaisun ainutlaatuisuutta.

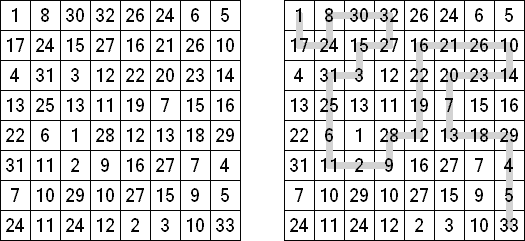
Numbrix on yksi logiikkapeleistä. Peli koostuu ruudukosta, jonka ruudut ovat osittain täytettyjä numeroita. Tehtävänä on siis täyttää tyhjät ruudut siten, että kaikki luvut on johdonmukaisesti yhdistetty vaaka- ja pystysuoraan. Lukuja ei saa yhdistää vinottain.

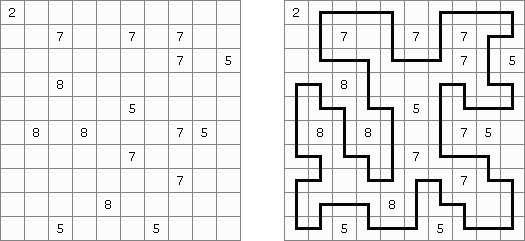
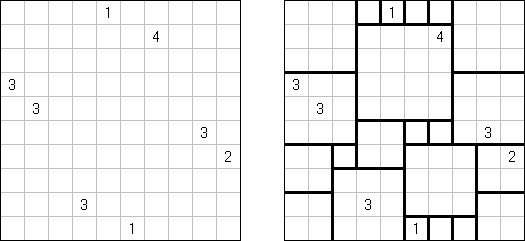
Shikaku ("Divide by Squares", "Divide by Box", "Number Area") on logiikkapeli. Se koostuu suorakulmaisesta ruudukosta, jonka koot ei määrätä tarkkaan. Osa ruuduista sisältää lukuja. Tehätävänä on piirtää ruudukon neliöiksi jakavat viivat siten, että jokaiseen neliöön sisältyy vain yksi sen pinta-alaa vastaava luku.

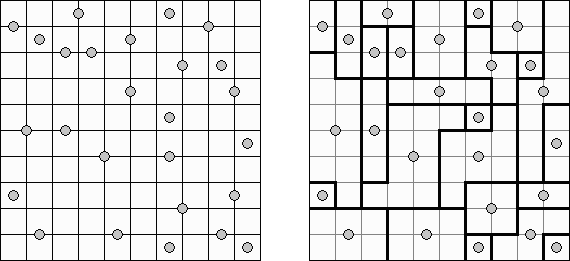
Galaxies ("Tentai Show") on logiikkaa ja geometriaa yhdistävä peli. Se koostuu suorakulmaisesta pisteitä sisältävästä verkosta. Tehtävänä on jakaa verkko alueiksi, joista jokainen sisältää ainoastaan yhden pisteen. Jokainen piste on oman alueensa symmetrian keskipiste.

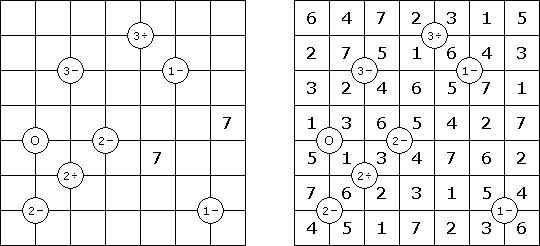
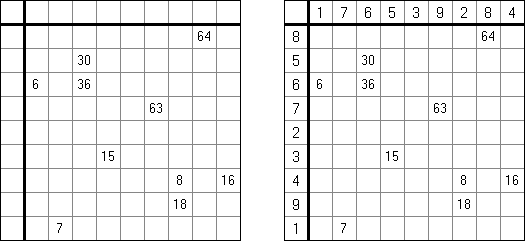
Pilvenpiirtäjä-tehtävässä vihjenumerot ovat ruudukon reunoilla (tunnetaan myös nimellä "Skyscrapers"). Vihjenumero kertoo montako pilvenpiirtäjää näkyy, kun kyseisestä ruudusta katsoo rivin tai sarakkeen suuntaan. Esimerkiksi: jos rivillä on 4 ruutua, ja esimmäisessä ruudussä on numero 4, näet vain tämän 4-kerroksisen rakennuksen, koska muut – matalammat – jäävät sen taakse piiloon. Tavoitteena on täyttää ruudut numeroilla 1:stä n:ään, missä n on ruudukon sivun pituus. Jokainen sarake ja jokainen rivi sisältää luvut vain kerran.

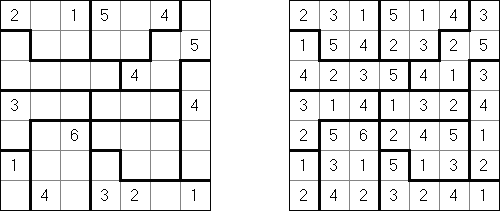
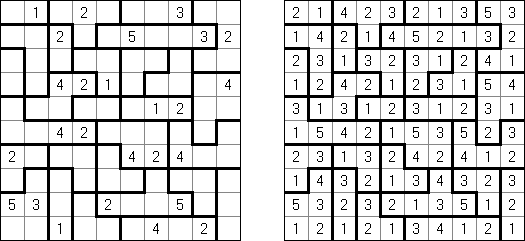
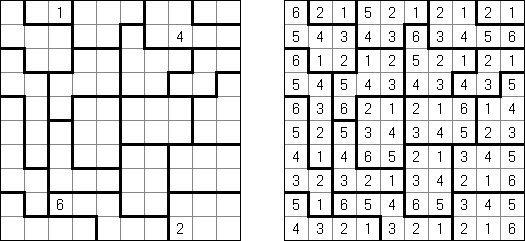
Hakyuu ("Ripple Effect", "Hakyuu Kouka", "Hakyukoka", "Seismic") on logiikkapelin laji. Peli koostuu suorakulmaisesta ruudukosta, joka on jaettu ns "huoneisiin". Tietyt huoneet sisältävät lukuja. Tehtävänä on täyttää tyhjät ruudut siten, että jokainen ruutu sisältää lukuja 1:stä n:ään, missä n on huoneen ruutumäärä. Jos ruuturivi tai sarake sisältää kaksi samaa lukua, niin niiden välissä olevien ruutujen lukumäärä on sama kuin kyseinen luku tai enempi. Esimerkiksi, jos sarakkeeseen sisältyy kaksi viitosta, niiden välissä täytyy olla vähintään 5 toisia lukuja sisältäviä ruutuja.

Grand Tour on logiikkapeli, jonka tehtävänä on piirtää itseään ylittämätön ja koskematon viiva, joka menee suorakulmaisen tai neliömäisen ruudukon kaikkien pisteiden läpi. Ratkaisun ainutlaatuisuuden takaamiseksi muutama piste on jo yhdistetty viivalla.

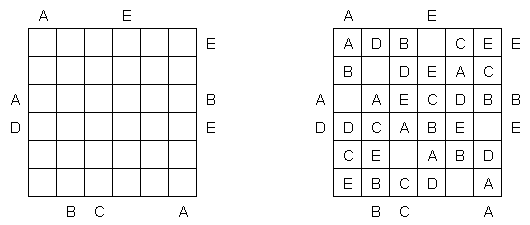
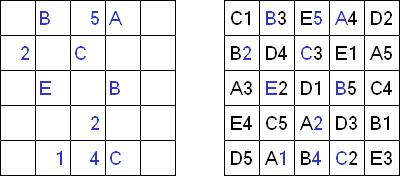
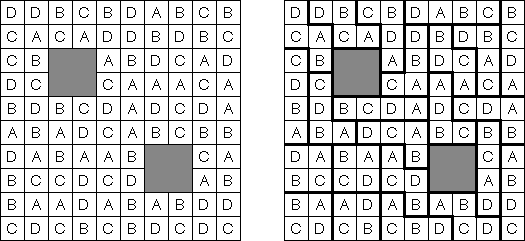
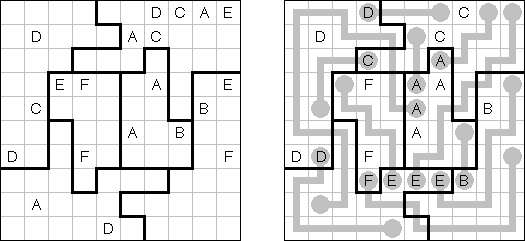
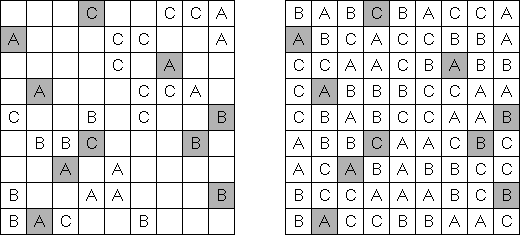
Easy as ABC ("ABC End View", "Last Man Standing") on kirjainpeli. Pelin tehtävänä on täyttää neliömäinen ruutu latinalaisin kirjaimin (esimerkiksi A:sta E:seen) siten, että jokainen kirjain sisältyy samaan riviin tai sarakkeeseen vain kerran. Jotkin ruudut voidaan jäädä tyhjiksi. Ruudukon marginaaleissa olevat kirjaimet osoittavat mikä kirjain on ensimäinen kyseisessä rivissä (sarakkeessa).

Clouds ("Rain Clouds", "Radar") on yksi Battleships-pelin muunnoksista. Vapaamuutoiseen ruudukkoon täytyy asentaa suorakulmaiset "pilvet" siten, että ne eivät koske toisiaan ollenkaan. Ruudukon marginaaleissa olevat luvut kertovat kuinka monta ruutua sisältyy pilviin. Pilvien lukumäärä ja koot ei mainittu, vaan on tunnettua, että pilvien sivu on vähintään kaksi ruutua pitkä.

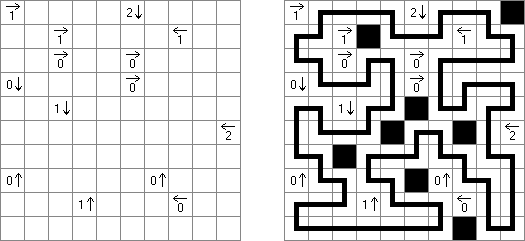
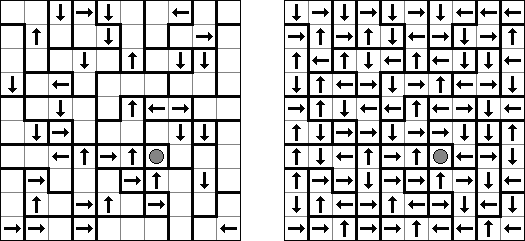
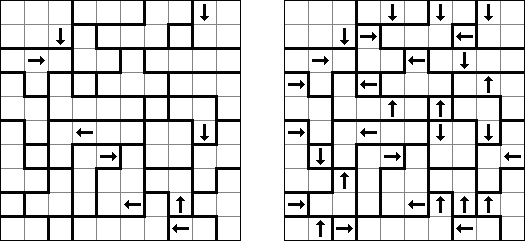
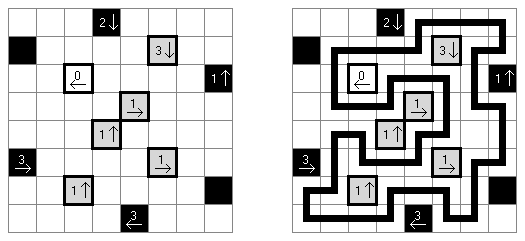
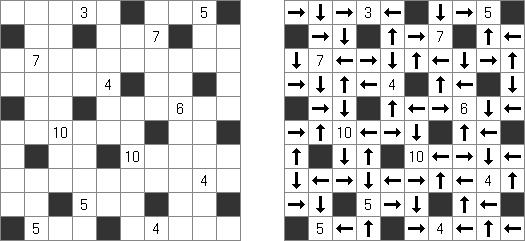
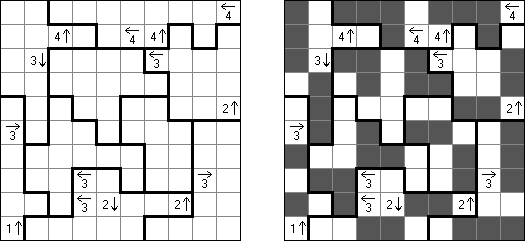
Yajilin ("Arrow Ring", "Straight and Arrow") on neliömäinen tai suorakulmainen logiikkapeli. Tehtävä sisältyy nuolia ja lukuja sisältäviä ruutuja. Ruuduissa oleva tieto tarvitaan mustien ruutujen sijoittamiseen oikeaan paikkaan. Tarkoituksena on piirtää itseään ylittämätön yhtenäinen silmukka, joka ei sisällä mustia ruutuja eikä ruutuja, joissa on nuolia ja lukuja. The grid may contain gray cells that can not be part of the loop.

• Ruuduissa olevat luvut kertovat kuinka monta mustaa ruutua on tiedyssä rivissä tai sarakkeessa nuolen osoittamassa suunnassa. Sellaiset ruudut itse ei pidetä mustina ruutuina.
• Jos ruudussa ei ole nuolta eikä se ole musta, niin se on silmukan osa.
• Ruudussa olevat luvut kertovat tarkkaan mustien ruutujen lukumäärästä. Esimerkiksi, jos ruudussa on kolmonen ja vasemmalle osoittava nuoli, niin kyseisen ruudun vasemmalla olevan rivin täytyy sisältää kolme mustaa ruutua.
• Mustat ruudut eivät saa koskea toisiinsa vaaka- eikä pystysuoraan.
• Ruudukossa voi olla mustia ruutuja, joita ei osoita yksikään nuoli.

Minesweeper on varmaan hyvin tunnettu Microsoft Windows -järjestelmän kaikille käyttäjille. Tehtävänä on sijoittaa miinat vapaisiin ruutuihin lukuja sisältäviä ruutuja käyttäen. Jokaisessa lukuruudussa näkyy monessako ruudun kahdeksasta naapuriruudusta on miina. Yhdessä ruudussa on vain yksi miina eikä lukuruudussa ole miinoja.

Minesweeper Battleships ("Battlemines") -peliin yhdistyy molempien suosikkipelien piirteitä. Tehtävänä on sijoittaa laivat ruudukkoon siten, että ne eivät koske toisiaan ollenkaan. Jotkin ruudut sisältävät lukuja, jotka kertovat kuinka monta laivan osaa sijaitsee kyseisen ruudun naapurissa (viistolinjat mukaan luettuna).

Heyawake on logiikkapeli, joka koostuu suorakulmaisesta ruudukosta, joka taas jakautuu ns "huoneisiin". Tietyihin huoneisiin sisältyy lukuja, jotka kertovat huoneessa olevien mustien ruutujen lukumäärästä. Jos luku puuttuu huoneesta niin tämä voi sisältää mustia ruutuja miten monta tahansa.

• Mustat ruudut eivät saa koskea toisiinsa vaaka- tai pystysuoraan (mutta koskeminen vinottain on salittu).
• Kaikki valkoiset ruudut on yhdistetty toisiinsa vaaka- tai pystysuoraan.
• Valkoisten ruutujen muodostama jatkuva viiva saa ristiä enintään kaksi huonetta.

Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten") on 10 ruutua sisältävä ruudukko. Tehtävänä on täyttää ruudukko siten, että jokaisessa rivissä on lukuja 0-9. Sarakkeessa voi olla muutama sama luku. Ruudukon alla oleva luku tarkoittaa sarakkeen kaikkien lukujen summaa. Vierekkäisissä ruuduissa olevien lukujen täytyy olla erilaisia, jopa jos ruudut koskevat toisiinsa vain vinottain.

Hundred koostuu neliömäisestä ruudukosta, jonka jokaisessa ruudussa on luku. Tehtävänä on sijoittaa lisäluvut siten, että jokaisessa rivissä ja sarakkeessa olevien lukujen summa on 100.

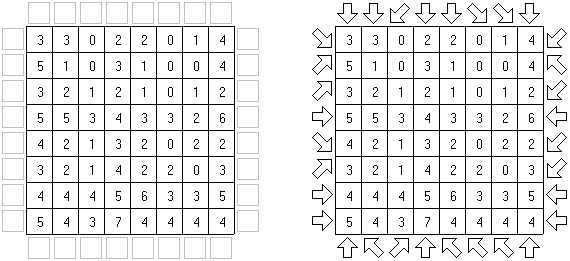
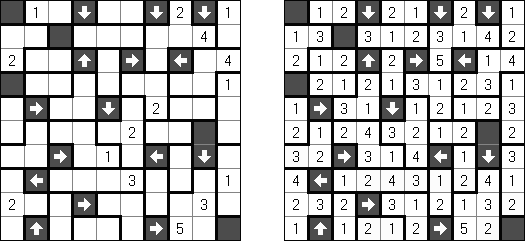
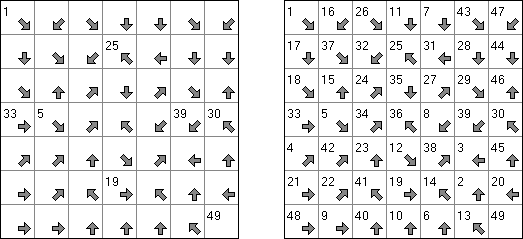
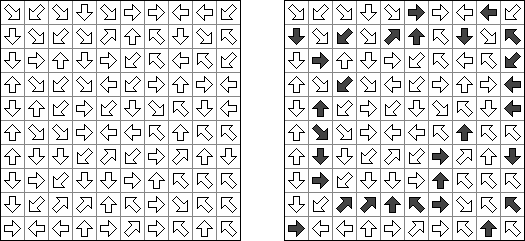
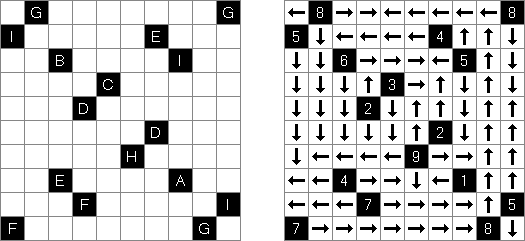
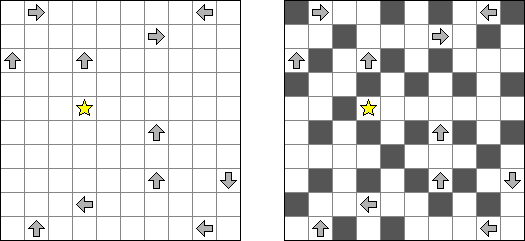
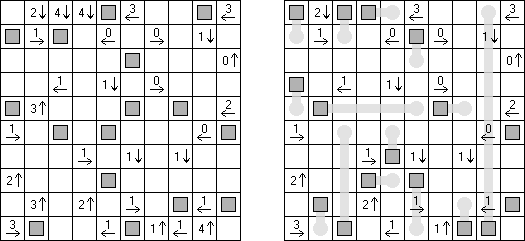
Arrows on yksi logiiikkapelin lajeista. Se on luvuilla täytetty suorakulmainen tai neliömäinen ruudukko. Pelin tehtävänä on sijoittaa nuolet ruudukon ulkopuolelle siten, että jokainen nuoli osoittaa ainakin yhtä lukuruutua. Ruudussa oleva luku kertoo kyseistä ruutua osoittavien nuolten lukumäärästä.

Mathrax on yksi logiikkapelin lajeista. Tehtävänä on täyttää luvuilla neliö siten, että jokaisessa rivissä ja sarakkeessa jokainen luku on ainoa. Ruudukon jotkin ruudut on jo täytetty. Viivojen risteydessä voi olla ympyriä lisäehtoineen:

• Ympyrässä on luku ja laskutoimitusmerkki. Luku tarkoittaa laskutoimituksen tulosta; laskutoimituksen kohteina on kaksi ympyrän naapurissa olevaa ja toisiinsa vinottain koskevaa lukua.
• E-kirjain tarkoittaa sen, että kaikki ympyrän naapurissa olevat luvut ovat parillisia ("E" on englannin sanan "even" ensimmäinen kirjain).
• O-kirjain tarkoittaa sen, että neljä ympyrän naapurissa olevaa lukua ovat parittomia в клетках вокруг кружка все четыре числа являются нечётными ("O" on englannin sanan "odd" ensimmäinen kirjain).

Str8ts ("Straights" on pokerin termi, joka tarkoittaa viittä peräkkäistä korttia) on kanadalainen Jeff Widderichin keksimä logiikkapeli. Neliömäiseen ruudukkoon sisältyy mustia ja valkoisia ruutuja. Tehtävänä on sijoittaa luvut valkoisiin ruutuihin siten, että mustien ja valkoisten ruutujen väliin syntyy peräkkäisten lukujen jono. Lukujen ei kuitenkaan tarvitse olla nousevassa tai alenevassa järjestyksessä (esim: 2-1-3-4). Jokaisen rivin ja sarakkeen valkoisissa ja mustissa ruuduissa olevien lukujen täytyy olla toistumatta. Mustissa ruuduissa olevat luvut eivät kuulu peräkkäisten lukujen jonoon.

Linesweeper on logiikkapeli, jonka säännöt ovat lähes samanlaisia kuin Minesweeper-pelin. Se on neliömäinen tai suorakulmainen ruudukko, jonka tietyissä ruuduissa on lukuja 0-8. Tehtävänä on piirtää jatkuva viiva ruutujen läpi siten, ettei viiva ylitä itseä eikä mene lukuja sisältävien ruutujen läpi. Ruudussa oleva luku ketoo kuinka monien lukuruudun ympärillä olevien ruutujen läpi viiva menee.

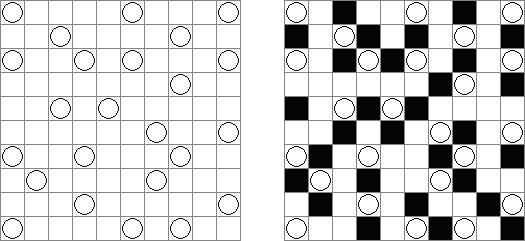
Binairo ("Binary Puzzle", "Takuzu", "Tohu wa Vohu") on lukuja 0 ja 1 käyttävä logiikkapeli. Suorakulmainen tai neliömäinen ruudukko on täytettävä luvuilla seuraavien sääntöjen mukaisesti:

• Jokainen rivi tai sarake sisältää yhtä monta ykköstä kuin nollaa (tai yhden enemmän kun ruudukon koot ovat parittomia).
• Sama luku voi olla vain kahdessa peräkkäisessä ruudussa.
• Jokaisen rivin ja sarakkeen täytyy olla ainutlaatuinen.

Walls on japanilainen Naoki Inaban keksimä logiikkapeli. Tehtävänä on sijoittaa valkoisiin ruutuihin vaaka- ja pystysuorat viivat siten, että kaikkien mustasta ruudusta lähtevien "säteiden" summittainen pituus on sama kuin kyseisessä ruudussa oleva luku.

Dominosa ("Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") on logiikkapeli, jossa käytetään dominopalikoita. Pelikentässä on vain lukuja ja tehtävänä on entistää dominopalikoiden välisten rajat.

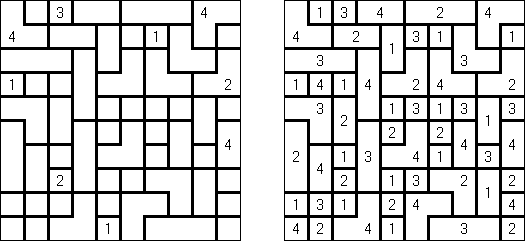
Patchwork ("Tatami") on logiikkapeli, joka koostuu samankokoisiksi alueiksi (ns "huoneiksi") jaetusta neliömäisestä ruudukosta. Tehtävänä on täyttää jokainen huone luvuilla 1:stä n:ään, missä n on kyseisen huoneen ruutumäärä. Jokainen rivi ja sarake sisältävät yhtä monta jokaisen lukulajin lukua. Viereiset ruudut, jotka koskevat toisiinsa vaaka- tai pystysuoraan, eivät saa sisältää samaa lukua. Sen logiikkapelin tietyissä lajeissa lukujen sijaan käytetään kirjaimia. Cross+A pystyy ratkaisemaan pelin sekä luku-, että kirjaintehtäviä.

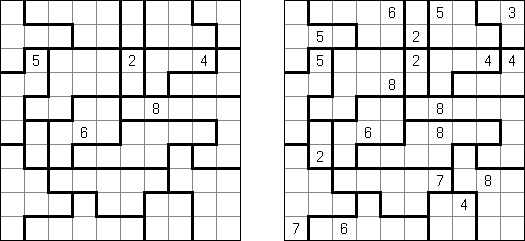
Knossos (Knossos on Kreetassa sijaitseva muinaiskaupunki ja palatsi sekä sokkelo, johon Minotauros vangittiin) on suorakulmainen tai neliömäinen ruudukko, jonka tietyissä ruuduissa on lukuja. Tehtävänä on jakaa ruudukko alueisiin (ns "huoneisiin") siten, että jokaisessa alueessa on vain yksi luku. Kyseinen luvun täytyy olla sama kuin alueen ympärysmitta.

Rekuto ("Recto") on neliömäinen tai suorakulmainen logiikkapeli. Sen ruudukon tietyissä ruuduissa on lukuja. Tehtävänä on piirtää viivat, jotka jakavat ruudukon neliömäisiksi ja suorakulmaisiksi alueiksi siten, että jokaisessa alueessa on vain yksi luku, joka on sama kuin alueen pituuden ja leveyden summa.

Neighbours on logiikkapeli, jonka ruudukon mitat ovat sattunaisia. Ruudukon tietyissä ruuduissa on lukuja tai kysymysmerkkejä. Ruudukko on jaettava alueiksi, joiden ruutumäärä on sama. Jokainen alue sisältää ainoastaan yhden ruudun, jossa on kysymysmerkki tai luku, joka kertoo kuinka monta "naapuria" kyseisellä alueella on. Kaksi aluetta pidetään viereisinä, jos niillä on yhteinen raja. Jos alueessa on kysymysmerkin sisältävä ruutu, kyseisellä alueella voi olla "naapureja" kuinka monta tahansa.

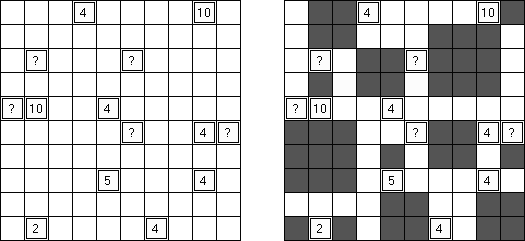
Four Winds ("Line Game") on logiikapeli, joka muodostuu mustia ja valkoisia ruutuja sisältävästä ruudukosta. Tehtävänä on piirtää suorat viivat, jotka alkavat mustista ruuduista ja menevät kaikkien valkoisten ruutujen läpi. Mustassa ruudussa oleva luku kertoo kuinka monta valkoista ruutua kuuluu kyseisestä mustasta ruudusta alkaviin viivoihin.

Shakashaka ("Proof of Quilt") on suorakulmainen tai neliömäinen logiikkapeli. Tehtävä sisältää mustat ja valkoiset ruudut, jonka osassa voi olla lukuja 0-4. Valkoisiin ruutuihin täytyy sijoittaa mustat kolmiot siten, että siitä muodostuu suorakulmaiset ja neliömäiset valkoiset alueet. Osa valkoisia ruutuja voidaan jättää tyhjiksi. Alueet voidaan suunnata vaaka- ja pystysuoraan sekä vinottain. Viereisillä valkoisilla alueilla ei saa olla yhteistä syrjää. Mustan ruudun luku kertoo kyseisen ruudun naapurissa olevien kolmioiden lukumäärästä.

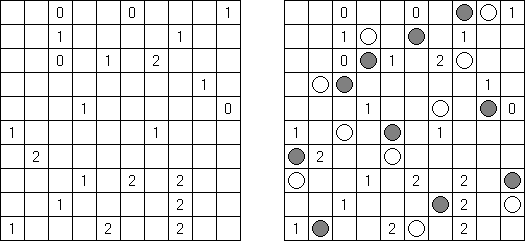
Kakurasu ("Index Sums") on suorakulmainen tai neliömäinen logiikkapeli, jonka tarkoituksena on sijoittaa mustat ja valkoiset ruudut oikein. Ruudukon ylhäällä ja vasemmalla olevat luvut kertovat riveihin ja sarakkeisiin sisältyvien mustien ruutujen "painojen" summasta. Ruudukon alhaalla ja oikealla olevat luvut sääntelevät mustien ruutujen "painoa" vastaavissa riveissä ja sarakkeissa. Ensimmäisessä rivissä ja sarakkeessa olevan mustan ruudun "paino" on 1, toisessa rivissä tai sarakkeessa 2 jne.

Mochikoro ("Mochinuri") on logiikapeli, joka muodostuu lukuja sisältävästä ruudukosta. Tehtävänä on sijoittaa valkoiset ja mustat ruudut siten, että siitä muodostuu suorakulmaiset ja neliömäiset valkoiset "saaret".

• Yksi valkoinen "saari" voi sisältää enintään yhden lukuruudun, jossa oleva luku tarkoittaa "saareen" kuuluvien valkoisten ruutujen lukumäärää.
• Tietyt "saaret" eivät sisällä lukuruutuja ollenkaan.
• Valkoiset alueest eivät saa koskea toisiinsa kyljillään, mutta kaikki valkoiset "saaret" koskevat toisiinsa vinottain.
• Ruudukossa ei saa olla yhtääkään 2 x 2 kokoista neliötä, joka koostuu ainoastaan mustista ruuduista.

Seethrough ("Doors", "Open Office") on neliömäinen tai suorakulmainen logiikkapeli, jonka jokainen solu tarkoittaa "huonetta". Tehtävänä on sulkea tai avata huoneiden "ovet". Avattu ovi antaa katsoa huoneesta toiseen tai muutaman huoneen läpi. Luku kertoo kuinka monta huonetta näkyy kyseisestä huoneesta tätä lukuun ottamatta. Pelissä ei saa olla toisistaan eristettyjä soluja, eli jokaisesta huoneesta pääsee toiseen.

Lighthouses on logiikkapeli, joka sisältää mustia ruutuja lukuineen ("majakat"). Luku tarkoittaa kyseisen majakan valaisemien laivojen lukumäärää. Majakka valaisee laivaa, kun ne ovat samassa rivissä tai sarakkeessa riippumatta siitä, onko niiden välissä toinen laiva tai majakka. Jokaisen laivan täytyy olla vähintään yhden majakan valaisema. Laivat sijaitsevat niin, etteivät ne koske majakoihin eivätkä toisiin laivohin ollenkaan.

Lighthouse Battleships:

Tapa on turkkilainen Serkan Yüreklin keksintö. Peli on valkoisista ruuduista koostuva neliömäinen tai suorakulmainen ruudukko. Tehtävänä on värittää tietyt ruudut mustiksi seuraavia sääntöjä noudattaen:

• Kaikki mustin ruutujen täytyy koskea toisiinsa sekä vaaka-, että pystysuoraan.
• Olemassa ei saa olla yhtääkään 2 x 2 kokoista keskittymää, joka koostuu ainoastaan mustista ruuduista.
• Tietyt ruudut sisältävät luvut tai kysymysmerkit ja ne aina jäävät valkoisiksi.
• Jokaien luku tarkoittaa sitä ympärillä olevien mustien ruutujen yhtenäistä keskittymää; kahden sellaisen keskittymän välissä täytyy olla vähintään yksi valkoinen ruutu.
• Kysymysmerkki tarkoittaa mita tahansa lukua, joka on nollaa suurempi.
• Lukujen asennolla tai niiden sijoittamisjärjestyksellä ei ole merkitystä.

Fobidoshi ("Forbidden Four") on japanilainen Naoki Inaban keksintö. Peli koostuu suorakulmaisesta tai neliömäisestä ruudukosta, jonka tietyissä soluissa on ympyröitä. Tehtävänä on sijoittaa tyhjiin soluihin ympyrät siten, että ne kaikki koskevat toisiinsa vaaka- tai pystysuoraan. Samassa rivissä tai sarakkeessa saa olla enintään neljä peräkkäistä ympyrää.

Island ("Tents Island", "Airando") on japanilainen Naoki Inaban keksimä logiikkapeli. Peli koostuu ruudukosta, jonka tietyissä ruuduissa on lukuja. Tehtävänä on värittää ruutuja mustiksi siten, että valkoisina pysyvät ruudut muodostavat yhden saaren. Lukuja sisältävät ruudut ovat saaren osia. Luku kertoo kuinka monta luvutonta ruutua on yletettävissä liikuttaessa saaren pintaa pitkin lukua sisältävän ruudun luota vaaka- ja pystysuoraan siihen asti kun toinen ruutu estää liikkumista.

Dominion on ruudukko, jonka ruudut sisältävät kirjaimia. Tarkoituksena on värittää tietyt ruudut seuraavia sääntöjä noudattaen:

• Ruudut voidaan värittää ainoastaan parittain eli kaksi mustaa ruutua koskevat toisiinsa vaaka- tai pystysuoraan. Sellaiset ruutuparit kutsutaan dominopalikoiksi.
• Dominopalikat saavat koskea toisiinsa ainoastaan vinottain.
• Kirjaimia sisältävät ruudut pysyvät valkoisina.
• Mustat ruudut jakavat ruudukon erillisiin alueisiin. Yhden alueen sisällä kaikki valkoiset ruudut koskevat toisiinsa vaaka- tai pystysuoraan.
• Saman kirjaimen sisältävät ruudut kuuluvat samaan valkoiseen alueeseen.
• Valkoiseen alueeseen aina sisältyy vaikkapa yksi kirjainruutu.

Tren – on japanilainen Shinichi Aokin keksimä logiikkapeli. Sen pelin nimi tarkoittaa japaniksi parkkipaikkaa (siellä ruuduista koostuva yksikkö tarkoittaa autoa ja ruudukko taas parkkipaikkaa). Peli koostuu neliömäisestä ruudukosta, jonka tietyissä ruuduissa on numeroja. Tehtävänä on laittaa ruudukkoon 1 x 2 tai 1 x 3 -mittaiset yksiköt siten, että jokainen numero sisältyy vain yhteen yksikköön. Kyseinen numero tarkoittaa etäisyyttä, jolle voidaan siirtää yksikkö. Yksikkö voidaan siirtää ainoastaan sen lyhyemmän osan suuntaan.

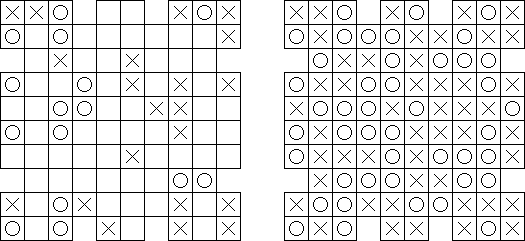
Vain kolme rivissä ("No Four in a Row") on vapaamuotoinen ruudukko. Ruudukon muutamissa ruuduissa on ristejä ja nollia. Tehtävänä on täyttää tyhjät ruudut siten, ettei vaaka- tai pystyrivissä olisi kolme samaa elementtiä peräkkäin.

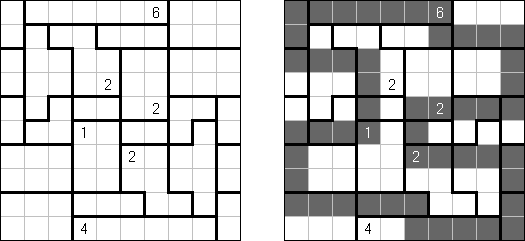
Corral ("Bag", "Cave") on suorakulmainen tai neliömäinen ruudukko, jonka tietyissä ruuduissa on lukuja. Tehtävänä on piirtää niiden lukujen ympärille yhtenäinen viiva. Luku tarkoittaa tästä näkyvissä olevien ruutujen lukumäärää vaaka- ja pystysuoraan viivan sisällä itse kyseinen luku mukaan luettuna.

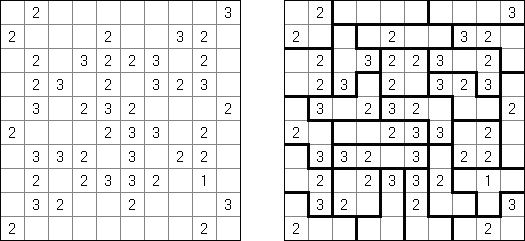
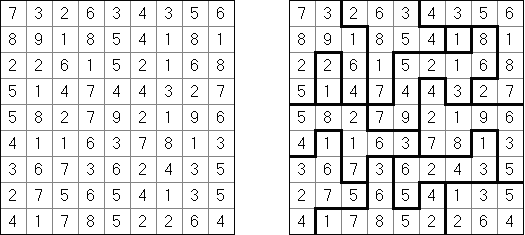
Neljä ruutua ("Foseruzu", "Four Cells") on logiikkapeli, joka koostuu neliö- tai suorakulmaruudukossa. Ruudukon muutamiin ruutuihin sisältyy lukuja. Pelin tarkoitus on jakaa ruudukko neljästä ruudusta koostuviin ryhmiin. Ruudussa oleva numero osoittaa kuinka monta ruudun sivua sisältävät ryhmien väliset rajat (ruudukon ulkorajat lukuun ottaen). Ryhmä voi sisältää lukuja kuinka monta hyvänsä tai se voi olla sisältämättä yhtäkään ruutua.

Viisi ruutua ("Faibuseruzu", "Five Cells", "Solomon's Keep"): pelin tehtävänä on jakaa ruudukko 5 ruudun ryhmiin.

Sutoreto ("Sutoretokurosu" – japanin ääntämyksen vääristämä englannin nimi "Straight Cross") on japanilainen Naoki Inaban keksimä logiikkapeli. Peli on suorakulma- tai neliöruudukko, johon sisältyy valkoisia ja muistia ruutuja. Muutamissa valkoisissa ruuduissa on numeroja. Tyhjät valkoiset ruudut tulee täyttää numeroilla siten, että mustien ruutujen välissä olisi lukujen nousevia sarjoja (lukujen ei kuitenkaan tarvitse olla peräkkäisiä, esim. 2-3-4 tai 5-4-7-6).

Renban on neliömäinen ruutu, joka jakautuu vapaamuotoisiin alueisiin. Pelin tehtävänä on täyttää ruudukko siten, että joka luku on ainoa jokaisessa rivissä, sarakkeessa ja alueessa. Kaikki alueen luvut ovat peräkkäisiä, kuitenkin niiden järjestys on vapaa (esimerkiksi 5-3-4).

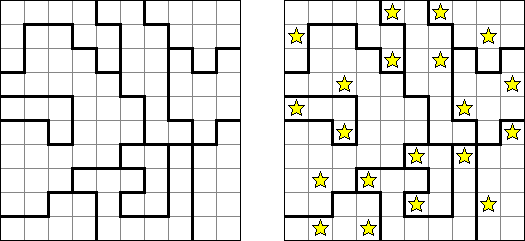
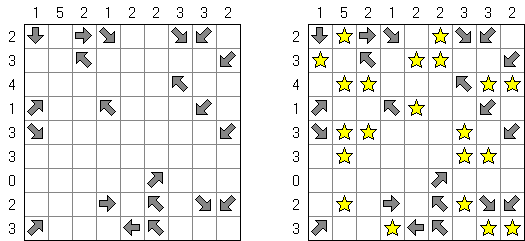
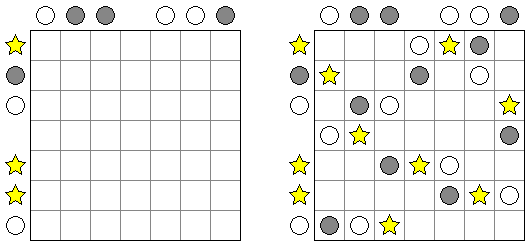
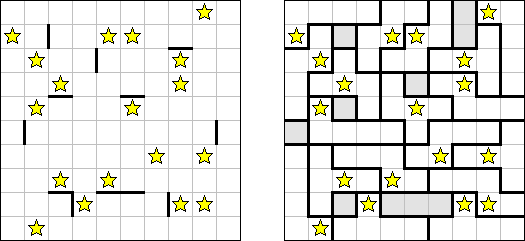
Buraitoraito (japanin ääntämyksen vääristämä englannin nimi "Bright Light") on japanilainen Naoki Inaban keksimä logiikkapeli. Peli koostuu suorakulma- tai neliöruudukosta, johon sisältyy valkoisia ja muistia ruutuja. Tehtävänä on laittaa tähdet valkoisiin ruutuihin siten, että mustassa ruudussa oleva numero vastaisi siitä ruudusta näkyvien tähtien määrää vaaka- tai pystysuorassa. "Katse" ulottuu siihen asti, kun pääsee ruudukon rajaan tai toiseen mustaa ruutuun.

Irasuto ("Illustration") on japanilainen Naoki Inaban keksimä logiikkapeli. Peli koostuu neliömäisestä tai suorakulmaisesta ruudukosta, johon sisältyy mustia ja valkoisia ruutuja. Muutamissa ruuduissa on lukuja. Pelin tehtävänä on järjestää mustat ja valkoiset ruudut noudattaen seuraavia sääntöjä:

• Valkoisessa ruudussa oleva luku tarkoittaa, kuinka monta muuta valkoista ruutua "on näkyvissä" vaaka- ja pystysuorassa. "Katse" ulottuu siihen saakka, kun vastaan tulee musta ruutu tai toinen valkoinen ruutu lukuineen.
• Mustassa ruudussa oleva luku tarkoittaa, monta muuta mustaa ruutua "on näkyvissä" vaaka- ja pystysuorassa. "Katse" ulottuu siihen saakka, kun vastaan tulee valkoinen ruutu tai toinen mustaa ruutu lukuineen.

Suguru ("Number Blocks") on Japanista kotoisin oleva Naoki Inaban keksimä logiikkapeli. Peli koostuu neliömäisestä tai suorakulmaisesta ruudukosta, joka jakautuu alueisiin. Tehtävänä on täyttää kaikki ruudut luvuilla siten, että jokaisessa alueella on lukuja yhdestä alueen ruutumäärään. Samoja lukuja sisältävät ruudut eivät voi koskea toisiinsa vaaka- eikä pystysuoraan.

Trinudo on neliömäinen tai suorakulmainen logiikkapeli. Muutamissa ruuduissa on lukuja. Ruudukko on jaettava 1-3 ruutuisiin alueisiin. Samankokoiset ruudut eivät saa koskea toisiinsa vaaka- eikä pystysuorassa. Jokainen luku tarkoittaa, kuinka monta ruutua sisältyy alueeseen, johon kyseinen luku myös kuuluu.

Creek ("Kuriku") on neliömäinen tai suorakulmainen ruutupeli. Linjojen risteyksissä on ympyröitä, joissa on lukuja 0-4. Luku tarkoittaa ympyrän vieressä olevien mustien ruutujen lukumäärää. Tehtävänä on järjestää valkoisia ja mustia ruutuja siten, että kaikki valkoiset ruudut koskisivat toisiinsa ainoastaan vaaka- tai pystysuorassa.

Gappy on looginen palapeli, jonka kenttänä on neliömäinen ruudukko. Pitää sijoittaa mustat solut ruudukkoon näin, että jokaisessa rivissä ja jokaisessa sarakkeessa olisi kaksi mustaa solua. Mustat solut eivät voi koskea toisiaan edes kulmillaan. Luvut ruudukon reunoilla kertovat montako valkoista solua pitää olla mustien solujen välillä rivissä tai sarakkeessa.

Norinori on loogisen palapelin laji. Sen kenttänä on suorakulmainen tai neliömäinen ruudukko, joka on jaettu erimuotoisiin osiin. Jokaisessa osassa pitää maalata mustaksi kaksi solua. Mustaksi maalattujen solujen pitää muodostua 2 x 1 tai 1 x 2 –muotoiset yhdistelmät (dominolaatat) huolimatta siitä, missä kulkee osan raja. Kaksi mustaa yhdistelmää eivät voi koskea toisiaan kyljillään (kun taas kulmillaan voivat).

Yonmasu ("Yonmasubunkatsu") on looginen palapeli, jonka keksi Naoki Inaba Japanista. Kenttänä on suorakulmainen tai neliömäinen ruudukko. Joissakin soluissa on ympyröitä. Pitää jakaa ruudukko muutamaan osaan, joista jokainen sisältäisi neljää solua, näin, että jokaisessa osassa olisi yksi ympyrä.

Tiilit ("Bricks") on loogisen palapelin laji. Pitää täyttää verkon numeroilla sillä lailla, jotta jokaisessa rivissä ja jokaisessa sarakkeessa ne eivät toistu. Joka tiilissä toinen numero on parillinen, toinen – pariton.

Numeroketju ("Number Chain") on lukupalapeli, jonka keksi Leonid Mochalov Venäjältä. Kenttänä on suorakulmainen tai neliömäinen ruudukko, jonka joka solussa on luku. Ruudukon vasemmassa yläkulmassa on luku 1, oikeassa alakulmassa on N; muuissa ruudukon soluissa on vapaavalintaiset luvut 1 - N asti. Pitää merkitä reitti ruudukon vasemmasta yläkulmasta oikeaan alakulmaan sillä lailla, jotta murtoviiva kulkisi N-solujen kautta, joiden sisällä on toistumattomia luvuja.

Kapetto ("Settokapetto" - japanin ääntämisellä vääristynyt englanninkielinen nimi "Set Carpets") on looginen palapeli, jonka keksi Naoki Inaba Japanista. Sen kenttänä on suorakulmainen tai neliömäinen ruudukko. Joissakin soluissa on lukuja. Pitää sijoittaa ruudukkoon suorakulmaiset osat näin, että jokaisessa osassa olisi yksi luku. Luku tarkoittaa osan pinta-alaa. Ruudukko voi sisältää soluja, jotka eivät kuulu mihinkään osaan.

Renkatsu on japanilainen Naoki Inaban keksimä logiikkapeli. Peli koostuu neliömäisestä tai suorakulmaisesta ruudukosta, joka jakautuu alueisiin. Tehtävänä on jakaa ruudukko alueisiin siten, että jokaiseen sisältyisivät lukuja 1..N. N on alueen ruutumäärä.

Eulero ("Kreikkalais-latinalainen ruudu") – lukuja ja kirjaimia sisältävä palapeli. Pitää sijoittaa symbolit ruudukkoon sillä lailla, jotta vastata seuraviin ehtoihin:

• Ruudukon joka solussa on vain yksi numero ja kirjain.
• Samassa rivissä ja sarakkeessa joka kirjaimen ja numeron pitää olla vain kerran.
• Kirjaimen ja numeron yhdistelmä voi olla ruudukossa vain kerran.

Anraikumozaiku (japanin ääntämisellä vääristynyt englanninkielinen nimi "Unlike Mosaic") on looginen palapeli, jonka keksi Naoki Inaba Japanista. Kenttänä on suorakulmainen tai neliömäinen ruudukko. Joissakin soluissa on ympyröitä. Pitää jakaa ruudukon suorakulmaisiin osiin sillä lailla, jotta jokaisessa osassa olisi uksi ympyrä. Mustat solut eivät kuulu mihinkään osaan. Saman solujen määrän sisältävät osat eivät voi koskea toisiaan pystysuunnassa eikä vaakasuunnassa.

Kurotto (japanin kielestä "mustat yksiköt") loogisen palapelin laji. Kenttänä on suorakulmainen tai neliömäinen ruudukko. Joissakin soluissa on ympyröitä (tyhjät tai lukuja sisältävät). Pitää sijoittaa mustat solut sillä lailla, jotta vastata seuraviin ehtoihin:

• Ei saa peittää ympyrän sisältävää solua mustalla.
• Mustat solut muodostavat aluet, joissa solut koskevat toisiaan pystysuunnassa ja vaakasuunnassa.
• Luku ympyrän sisällä vastaa pystysuunnassa ja vaakasuunnassa toisiaan koskevienmustien solujen pinta-alaan.
• Jos ympyrä ei sisällä lukua siihen voi liittyä eri pinta-alan aluet mustista soluista.

Tasukuea (from Japanese, literally "find squares") is a type of logic puzzles. It is played on a rectangular or square grid with numbers or question signs in some cells. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers or question signs can not be blacken.
• Black cells form square areas, that must not be orthogonally adjacent.
• A number in a circle indicates the total number of black cells in areas orthogonally neighboring the numbered cell.
• A cell with a question sign must have at least one adjacent black cell.
• All the white cells must be connected horizontally or vertically.

Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.

Araf (from Turkish, literally "purgatory"; original Japanese name - "Aidabeya") is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.

Kabingurodo (japanin ääntämisellä vääristynyt englanninkielinen nimi "Curving Road") on looginen palapeli, jonka keksi Naoki Inaba Japanista. Kenttänä on suorakulmainen tai neliömäinen ruudukko. Joissakin soluissa on ympyröitä. Pitää sijoittaa ruudukkoon mustat solut noudattaen seuraavia sääntöjä:

• Ei saa sijoittaa mustaa solua sinne, missä on ympyrä.
• Mustat solut eivät voi koskea toisiaan kyljillään, kun taas kulmillaan voivat.
• Kaikki valkoiset solut muodostavat yhteistä valkoista kenttää elikä koskevat toisiaan kyljillään.
• Jokaisen reitin, joka kulkee valkoisten solujen kautta toisesta ympyrästä toiseen, pitää kääntyä vähintään kaksi kertaa.

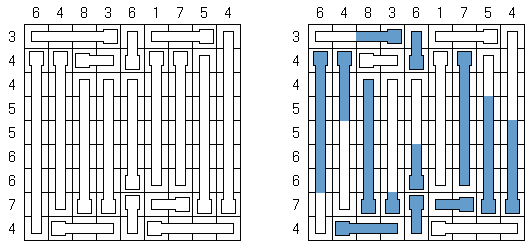
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.

Snake ("Tunnel") is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.

Peintoeria ("Paint Area") is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All cells of a region must have the same color.
• A cell with a number indicates how many black cells are adjacent to it.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the same color.

Irupu ("I-Loop") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.

Sashigane (from Japanese, literally "carpenter's square") is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.

Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

Chocona ("Chocolate") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any number of cells may be blackened.
• The black cells must form rectangles, independently of the region borders.
• The black rectangles must not be orthogonally adjacent.

Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.

LITS ("Nuruomino") is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.

The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.

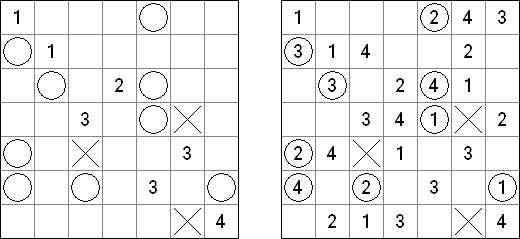
Nanbaboru ("Number Ball") consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.

Tairupeinto ("Tile Paint", "Crazy Pavement") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.

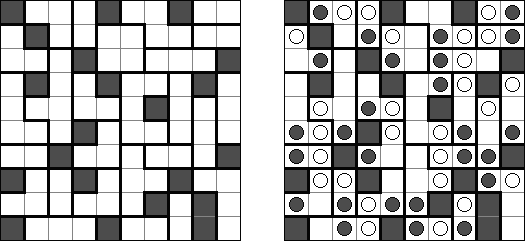
Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.

Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.

Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.

Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.

Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.

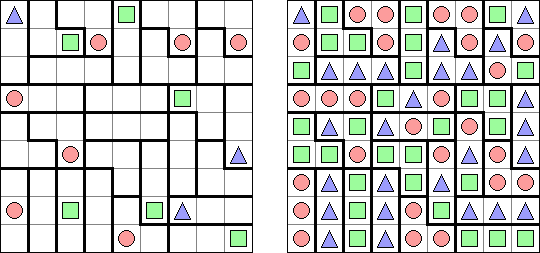
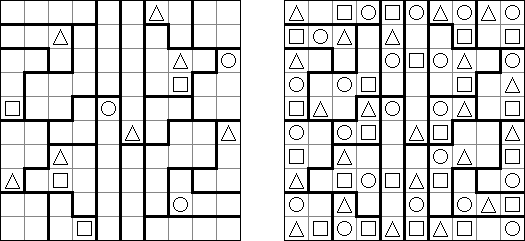
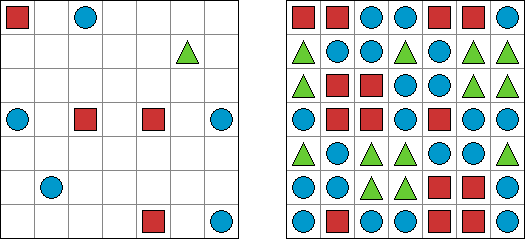
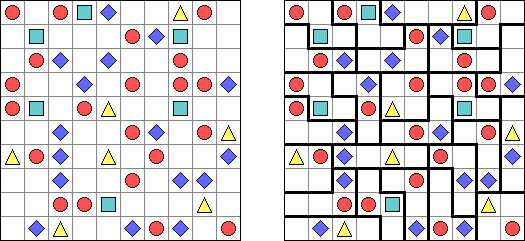
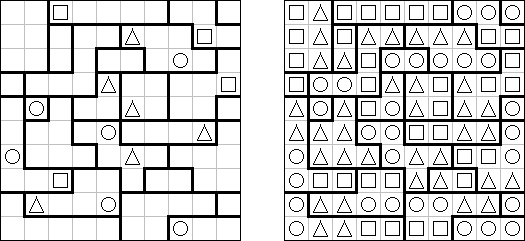
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.

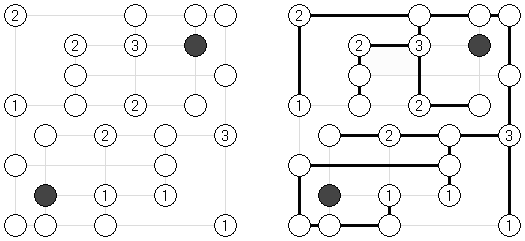
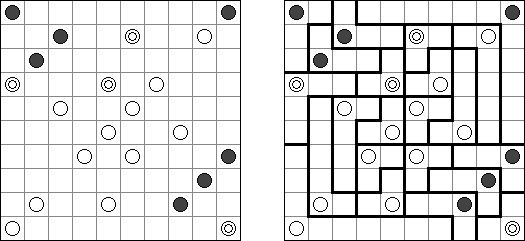
Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.

Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.

Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.

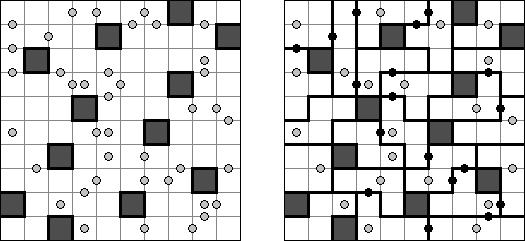
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.

Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.

Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.

Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.

Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.

Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:

• White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle.
• Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.

Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.

Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.

Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.

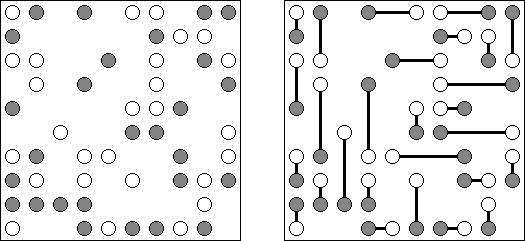
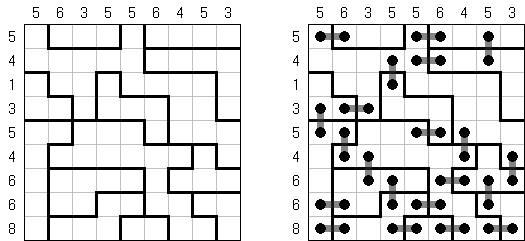
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.

Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.

Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.

Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.

Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:

• Each region contains exactly one arrow.
• Each two arrows are paired, they point to each other. There are no unpaired arrows.
• Two regions with paired arrows must not be horizontally or vertically adjacent.
• Between two paired arrows no other arrow must be placed.

Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.

Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.

Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.

Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• The black cells divide the grid in areas of white cells. Each area contains one cell with a number.
• Each area must have the same number of white cells as the number it contains (including the numbered cell).
• Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide.
• If two stripes are connected diagonally, the length of the stripes must be different.

Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.

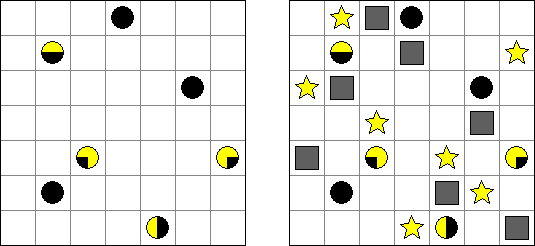
Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.

Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.

Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells).
• Two black cells must not be orthogonally adjacent.
• All of the white cells must be connected.

Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.

Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:

• Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake").
• Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed.
• Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached.
• The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.

Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.

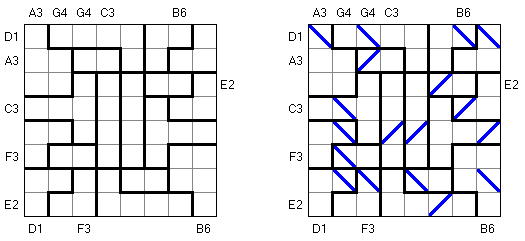
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.

Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.

Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• Two regions with the same amount of black cells must not be orthogonally adjacent.
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.

Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:

• Black cells must not be orthogonally connected.
• A cell with a number may be blacken.
• All the white cells must form an orthogonally continuous area.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.
• Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.

Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:

• A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally.
• A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all.
• A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells.
• Two snakes of the same length must not be orthogonally adjacent.
• A cell with a cross cannot be an end of a snake.

Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:

• Start at any stone.
• When a stone is encountered, it is picked up.
• When a stone is picked up, the direction can be changed.
• It is not allowed to reverse the direction.

Water Fun ("Aquarium") is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.

Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.

Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.

Santoitchi ("San to itchi"; from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• All white cells must be divided on regions having the size of exactly three cells.
• Two black cells must not be orthogonally adjacent.
• Each region contains a number.
• A number indicates how many black cells share an edge with that region.

Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.

Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.

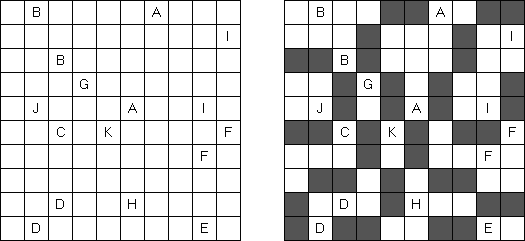
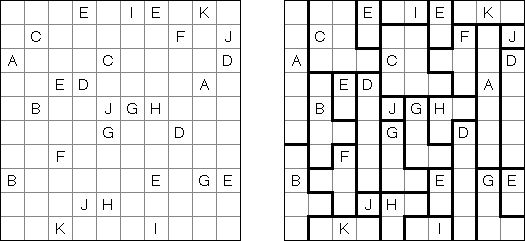
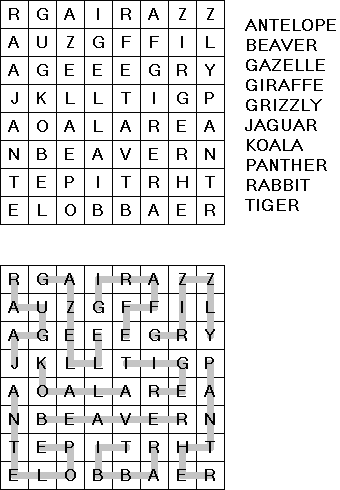
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.

Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.

EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.

Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.

Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.

Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.

Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:

• All black cells in a region must be connected horizontally or vertically.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• If all stones "fall down", they must cover exactly the bottom half of the grid.

Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.

Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.

Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.

Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:

• Cells with letters, circles or triangles are always white.
• White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide.
• A path from S to G includes all cells with circles and no cells with triangles.
• No 2 x 2 cell area within the grid can have the same color.
• All white cells must form an orthogonally continuous area.
• White cells must not form a loop.

Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:

• All black cells create a single connected group.
• No 2 x 2 cell area within the grid can contain all black cells.
• Numbered cells must not be black.
• Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.

Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.

Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:

• Each region contains one black circle.
• Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.

Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.

Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.

Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.

Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.

Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)

Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.

Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.

Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.

Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:

• Black cells form an area of square shape.
• No black areas touch each other horizontally or vertically (only diagonally).
• Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size.
• Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.

Golem Grad (an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:

• The black cells divide the grid into areas of white cells ("islands"), each containing at most one number.
• Two islands may not be connected.
• The island must have the same number of white cells as the number it contains.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the black color.
• All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid.
• Snakes must not cross each other.

Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:

• No two horizontally, vertically or diagonally adjacent cells contain a digit.
• The numbers across the top and down the left equal the row and column totals for the cells with numbers.
• The numbers across the bottom and down the right are the sums of numbers in the rows and columns.

Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.

Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• White cells form a path exactly one cell wide.
• Cells with circles are always white.
• A cell with a circle must have exactly one white cell adjacent to its side.
• A white cell without a circle must have at least two orthogonally adjacent white cells.
• A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself.
• All the white cells must be connected horizontally or vertically.
• No 2 x 2 cell area within the grid can have the same color.

Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:

• The white circle indicates that the sun is closer to the star than the moon.
• The black circle indicates that the moon is closer to the star than the sun.
• The star outside the grid indicates that the circles are at equal distance from the star in that row or column.

Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.

Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.

Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.

Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.

Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)

Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.

Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.

Nuraf ("Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells divide the grid into areas of white cells ("islands").
• Cells with numbers are always white.
• Two islands may not be connected.
• All of the black cells must be connected.
• No 2 x 2 cell area within the grid can have the black color.
• Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.

Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.

Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.

• The same arrows cannot be placed in adjacent cells.
• Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached.
• A cell with a number indicates a total number of arrows that leads to this cell.

Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.

Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.

Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.

Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)

Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.

Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.

Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.

Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.

Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.

Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.

Meandering Numbers (also known as "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)

Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.

Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.

From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.

Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.

Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.

Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.

Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)

Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.

Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).

Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.

Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).

Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.

Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.

Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.

Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.

Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.

Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.

SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.

Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border.
• A cell with a number indicates how many cells in the region must be blackened.
• No two black areas may share an edge.

Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.

Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.

Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.

Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.

Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.

Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.

Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:

• The black cells form "islands". No two islands may share an edge; islands may be connected through their corners.
• If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island).
• All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners.
• If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).

Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.

Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All white cells form one orthogonally connected area.
• A line of connected white cells cannot go through two or more region borders.

Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.

Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.

Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally).
• A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer.
• Each block contains exactly one number or a question mark.
• All blocks form "chains". A chain is a group of two or more blocks, connected through their corners.
• Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.

Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened.
• Blackened cells should not share an edge.
• All the white cells must be connected inside a region (it's possible for a region to have no white cells).
• If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions.
• All the white cells must form an orthogonally continuous area.

Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its N^th entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.

Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.

Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.

Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected horizontally or vertically (they form a "block").
• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any amount of cells may be blackened (all cells may stay white).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All blocks of black cells must be connected to each other through their corners.
• No 2 x 2 cell area within the grid can contain all black cells.

Kazoku ("Kazoku shashin"; from Japanese, literally "family photo") is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.

Tontonbeya (from Japanese, literally "gambler") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.

Konteksti ("Context") is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:

• All the white cells must be connected horizontally or vertically.
• A cell with a number can be blacken. Two black cells must not be orthogonally adjacent.
• The number in a white cell indicates the number of orthogonally adjacent black cells.
• The number in a black cell indicates the number of diagonally adjacent black cells.

Word Finder ("Word Search", "Word Seek", "Word Sleuth", "Mystery Word") on logiikkapeli, joka koostuu neliömäisiä tai suorakulmaisia kirjaimia sisältävästä ruudukosta. Tarkoituksena on löytää kirjainruudukkoon piilotettu sana. Sana luetaan murtoviivan pitkin ja tämä voi taipua vain suorakulmaisesti. Kukin kirjain voidaan käyttää vain yhdessä sanassa.

Pelin aloittamiseksi tulee laittaa sanalista. Sen lisäksi voi myös mainita avainsana, joka muodostuu pelin ratkaisemisen jälkeen käyttämättömiksi jääneistä sanoista.

Yhdeksän kirjainta ("Nine Letters") on yksi Word Finder-palapelin lajista. Se on kirjaimia sisältävä ruudukko, joka on jaettu alueisiin kooltaan 3 x 3. Pitää löytää sanoja, joissa on 9 kirjainta. Sanat on piilotettu jokaisen alueen sisälle.

Hämähäkinverkko ("Spider Web") koostuu viivoilla toisiinsa yhdistyneistä ympyröistä. Ympyröistä on kirjaimia. Pitää löytää katkeamaton ketju ympyröitä, jotka sisältävät tarvittavan sanan kirjaimia.

Labyrintti ("Maze") on sotkeutuneista reiteistä koostuva rakenne. Tässä palapelien lajissa pitää löytää tie kahden merkityn pisteen välillä. Ohjelma antaa mahdollisuutta luoda erimuotoisia labyrintteja, ei ainoastaan suorakulmaisia tai neliömäisiä.