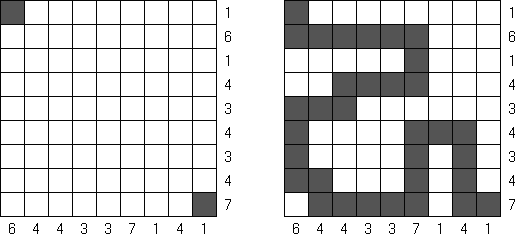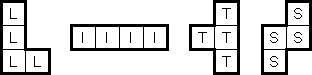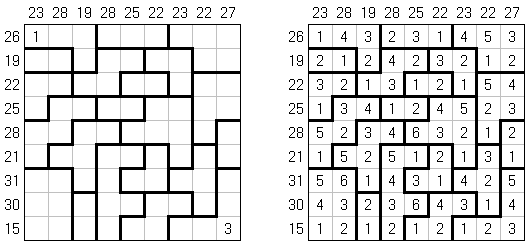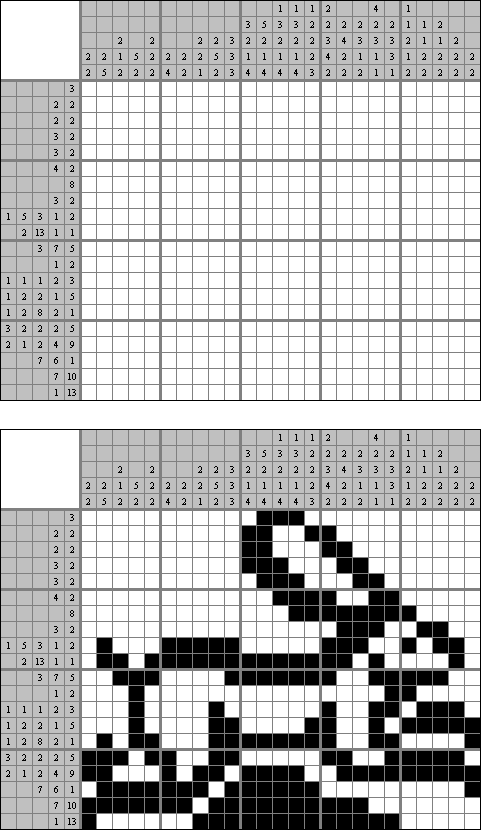
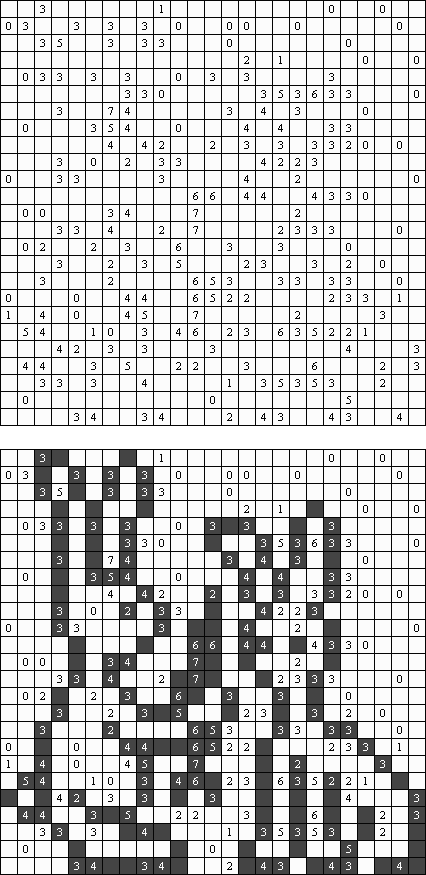
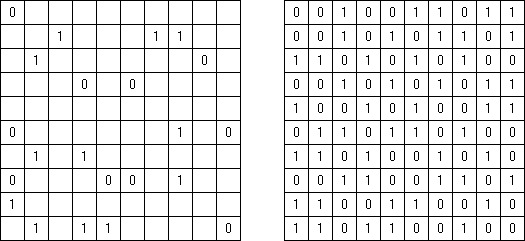
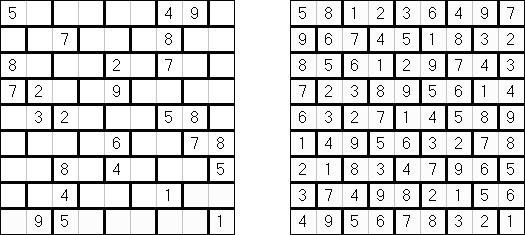
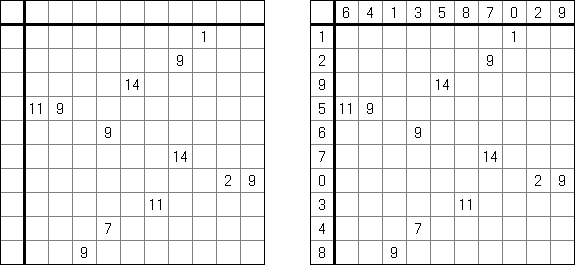
Cross+A Łamigłówki

Cross+A rozwiązuje i tworzy mnóstwo różnorodnych łamigłówek i zagadek logicznych. Stworzoną łamigłówkę można zachować jako plik graficzny (wspiera formaty BMP, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF, metapliki Windows i pliki CorelDRAW). Także dostępny tryb pakietowy tworzenia łamigłówek.

Nonogram ("Obrazek logiczny"; znany również jako "Malowanie liczbami", "Paint By Numbers", "Griddler", "CrossPix", "Hanjie") – łamigłówka polega na malowaniu obrazków przez zaznaczenie właściwych pól diagramu. Liczby z lewej strony i u góry kołumny określają, ile grup znajduję się w rzędzie oraz ile czarnych pól zawiera każda grupa. Pomiędzy grupami musi być co najmniej jedno pole puste.

Program Cross+A może rozwiązywać łamigłówki czarno-białe i kolorowe.

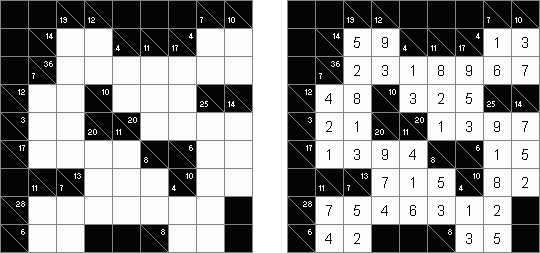
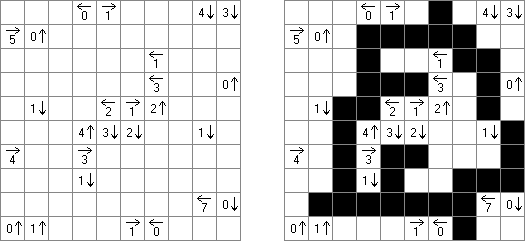
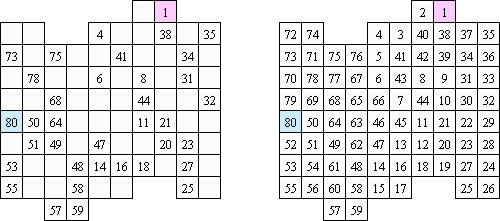
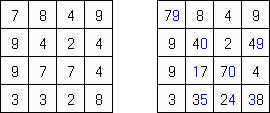
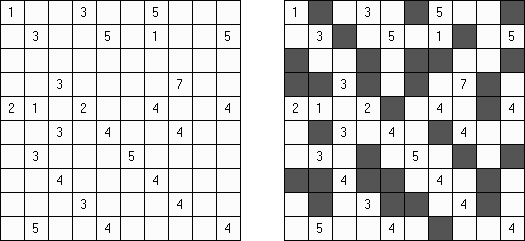
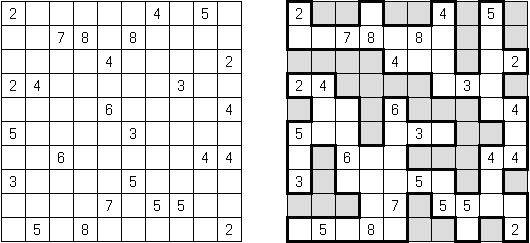
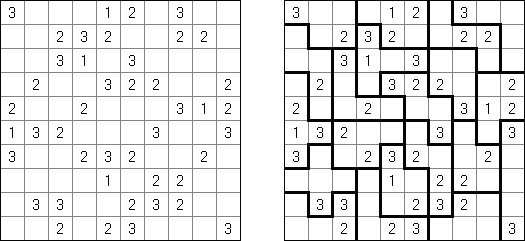
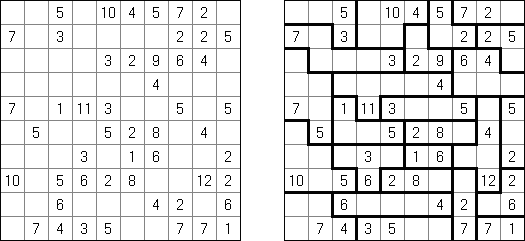
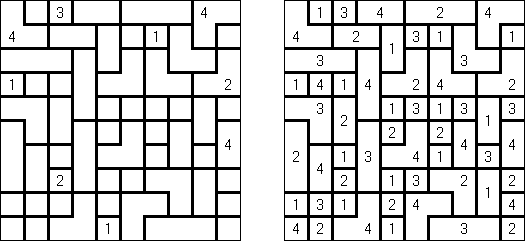
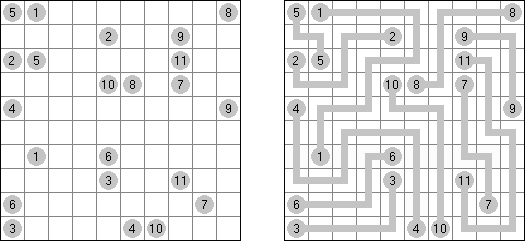
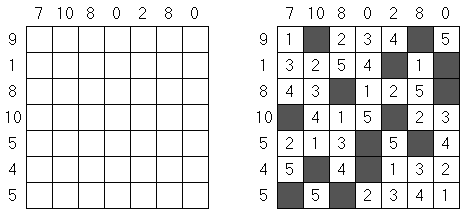
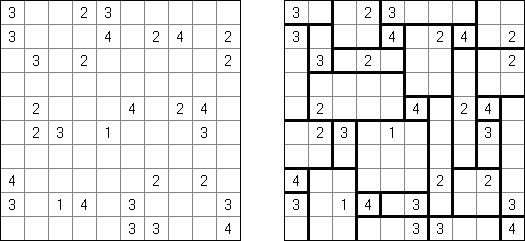
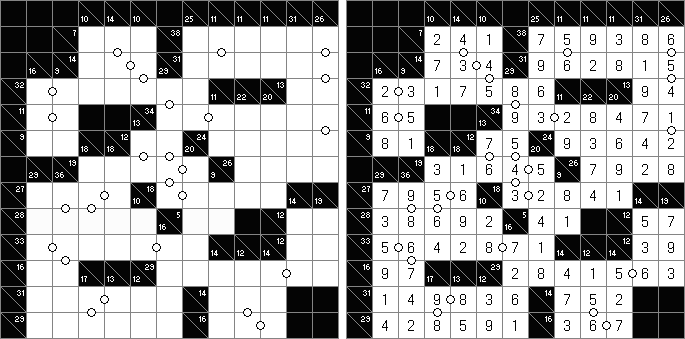
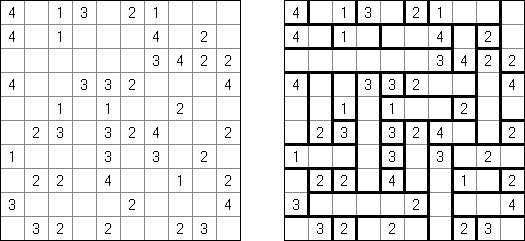
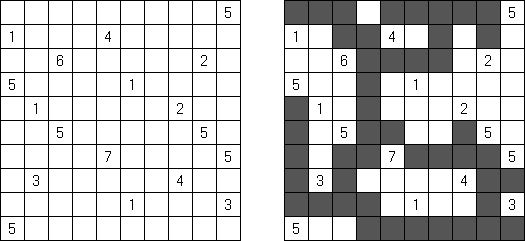
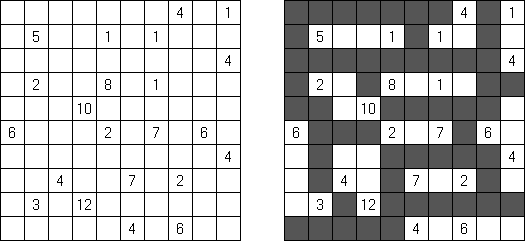
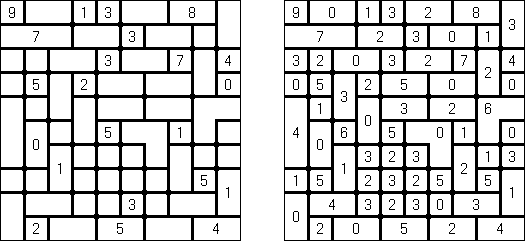
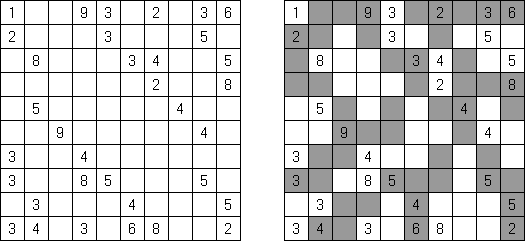
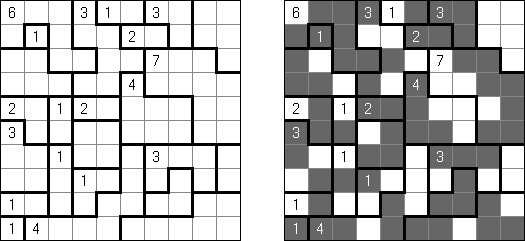
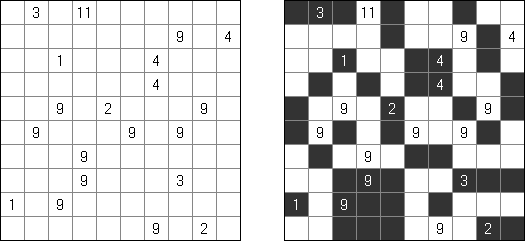
Kakuro (znany również jako "Krzyżówka liczbowa", "Cross Sums") – to łamigłówka liczbowa, o której często mówi się, że jest matematycznym odpowiednikiem krzyżówki. Należy wypełnić diagram ciągami cyfr od 1 do 9, przy tem uważać na pola nieaktywne (czarne). Liczba w prawym górnym rogu czarnego pola to suma cyfr ciągu poziomego, liczba w lewym dolnym rogu – suma cyfr ciągu pionowego. Na przykład: dana suma wynosi 6, więc możliwe rozwiązanie 1 i 5, 2 i 4. Żadna cyfra w ciągu nie może się powtarzać.

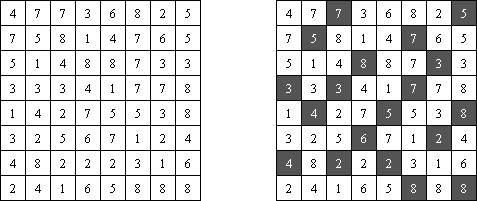
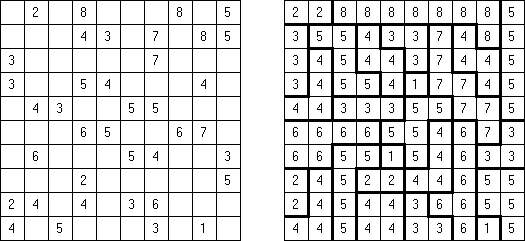
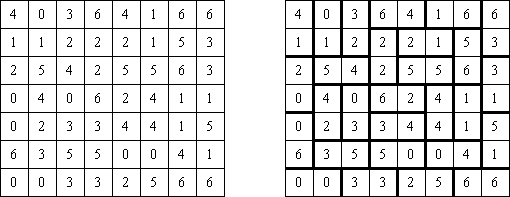
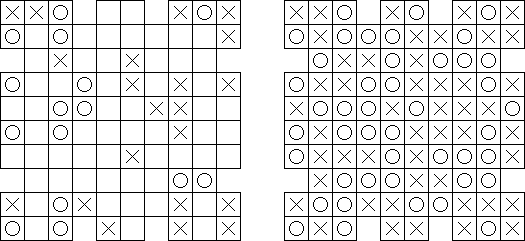
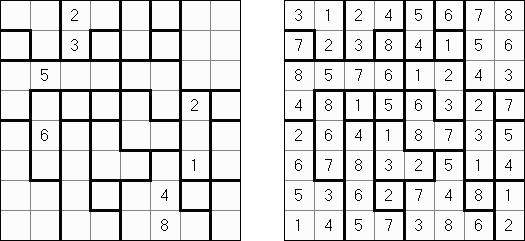
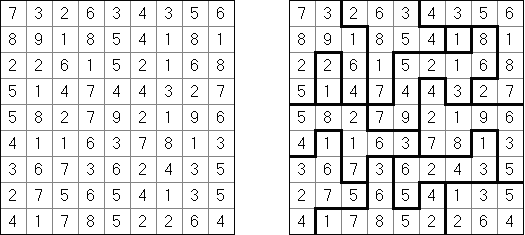
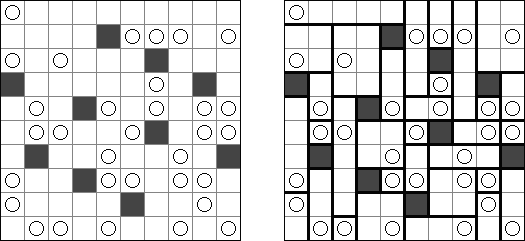
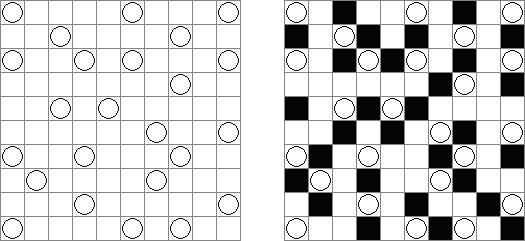
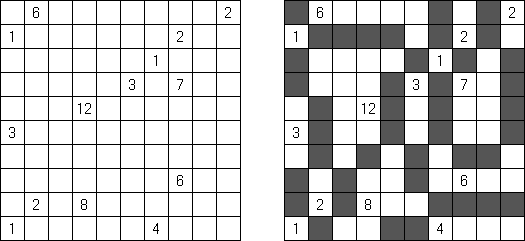
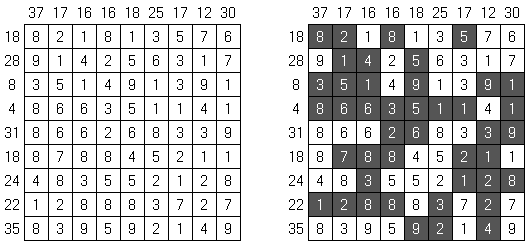
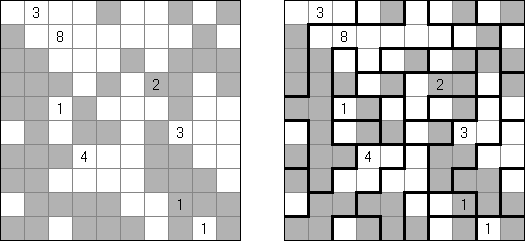
Hitori – to logiczna łamigłówka, która polega na skreślaniu powtarzających się liczb, przy tym każda z nich może występować w rzędzie lub kolumnie dokładnie raz. Skreślone pola nie mogą się stykać bokami, tylko kątami. Jasne pola muszą utworzyć jedną spójną białą całość. To znaczy, że żadne z nich nie może być izolowane.

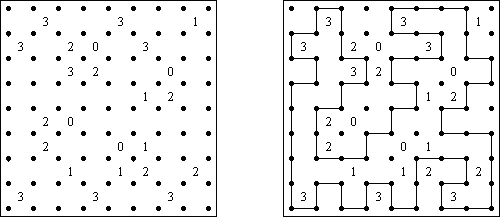
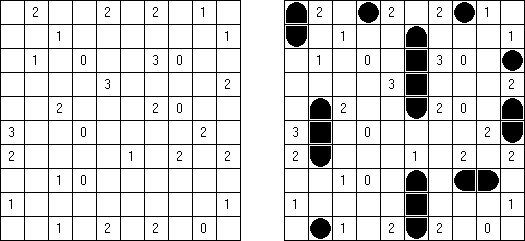
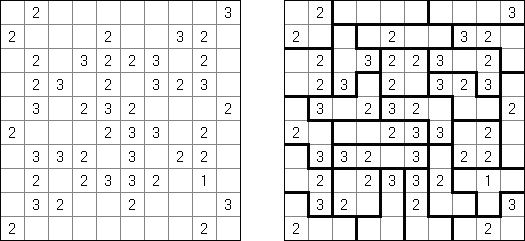
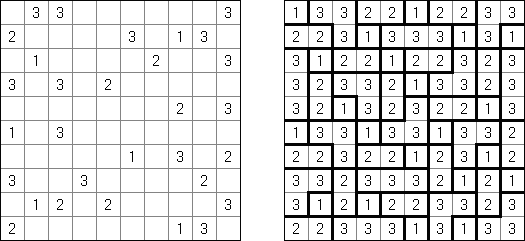
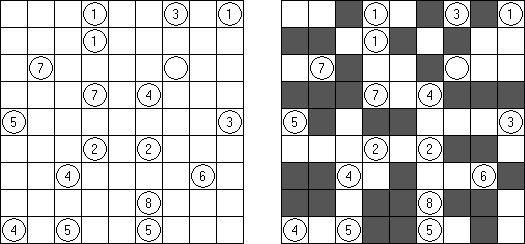
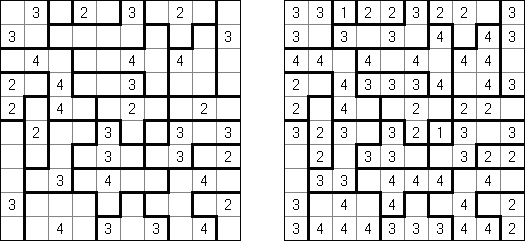
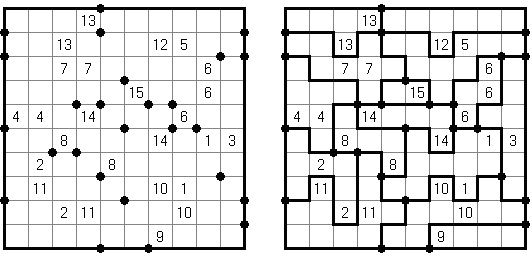
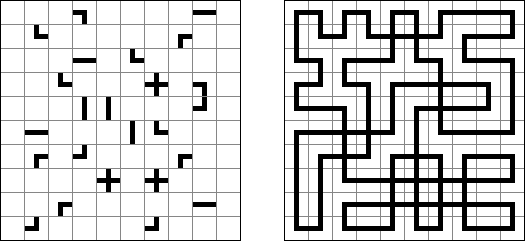
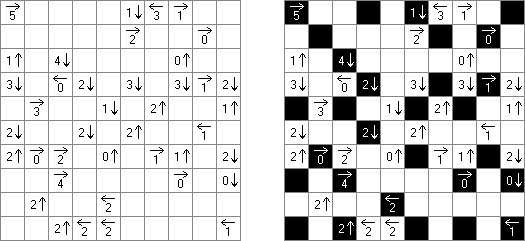
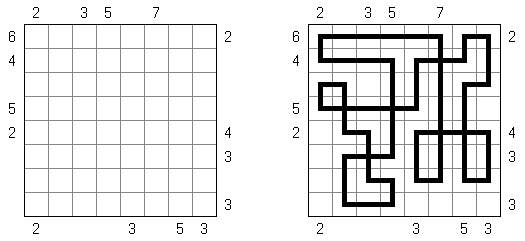
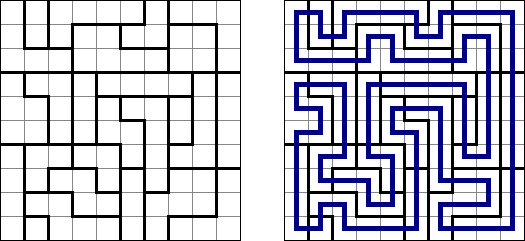
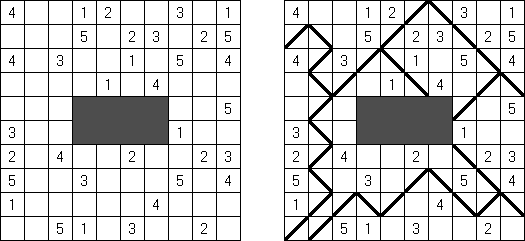
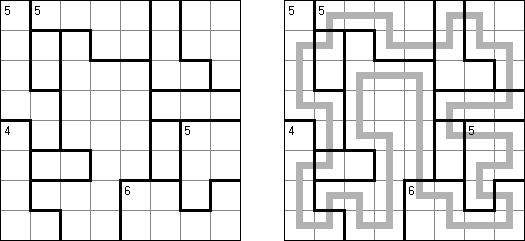
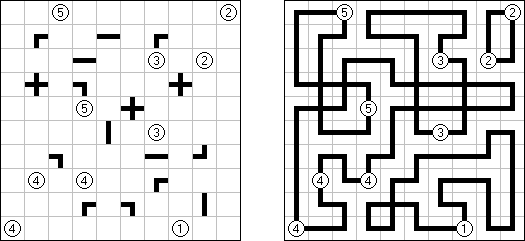
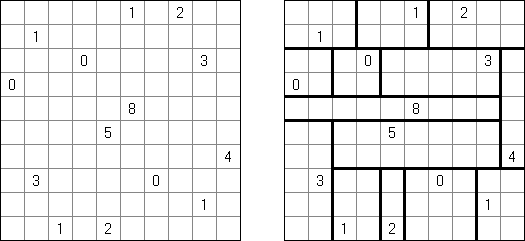
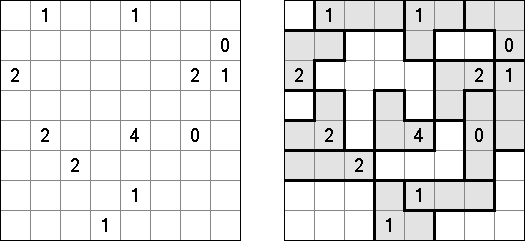
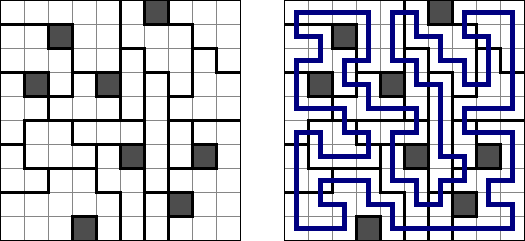
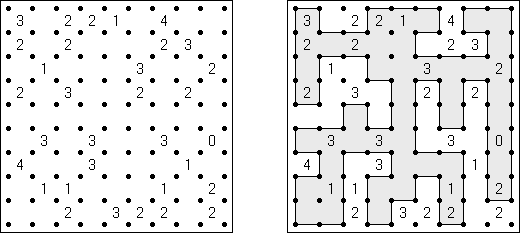
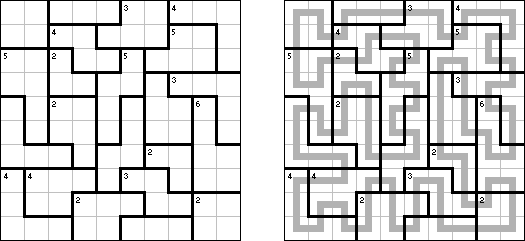
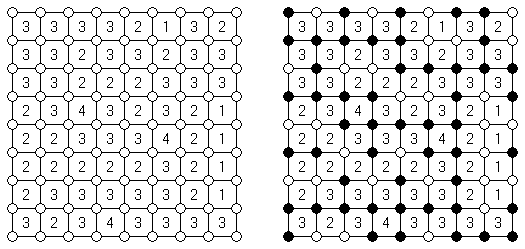
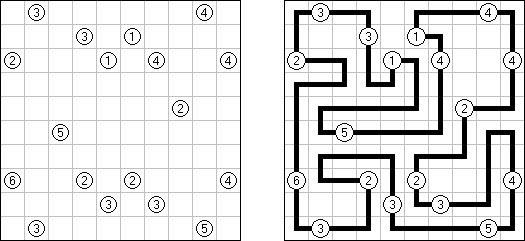
Slitherlink ("Pokropka"; znany również jako "Wielokropka", "Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin", "Great Wall of China") – to logiczna łamigłówka, podobna do labiryntu. Należy poprowadzić łamaną linie zamkniętą pomiędzy kropkami i sformować pojedynczą pętlę bez skrzyżowań i odgałęzień. Cyfra oznacza ile odcinków linii otacza kratkę. Jeśli kratka nie zawiera żadnej cyfry, to oznacza że wokół niej może znajdować się dowolna ilość linii.

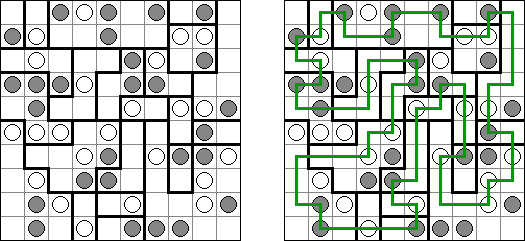
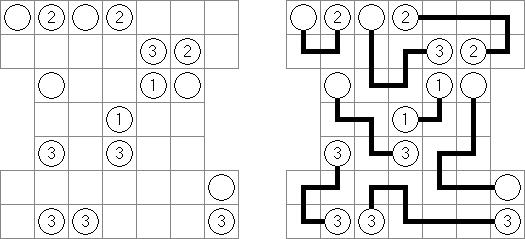
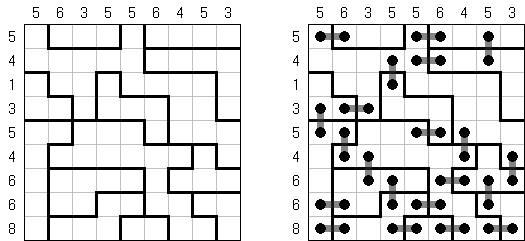
Link-a-Pix ("Paint by pairs") – to łamigłówka liczbowa w której wszystkie cyfry oprócz jedynki, mają swoją parę. Należy odnaleźć każdą parę i połączyć je w całość. Ilość pól między cyframi z każdej pary musi dorównać liczbie na końcach linii. Linia może być łamana, pozioma i pionowa, lecz nie ukośna. Linie nie mogą się ze sobą stykać ani przecinać.

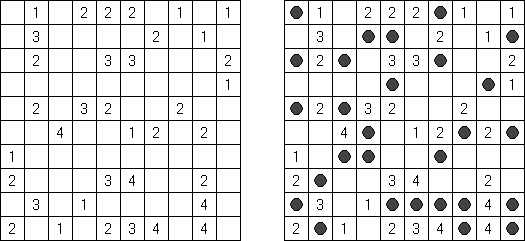
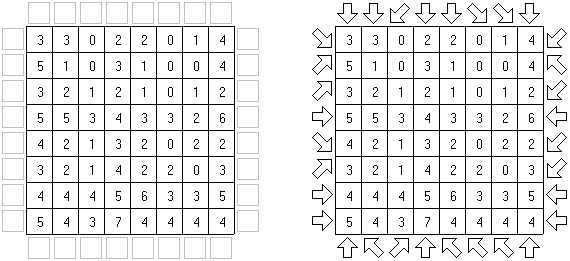
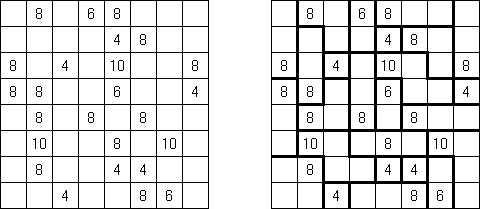
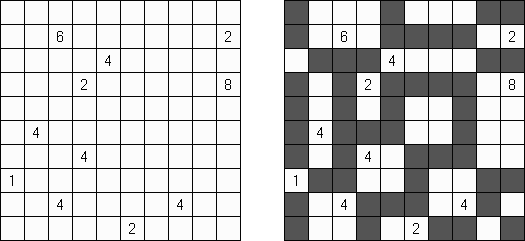
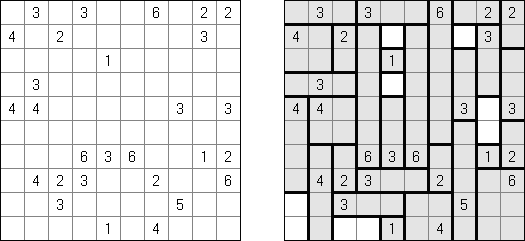
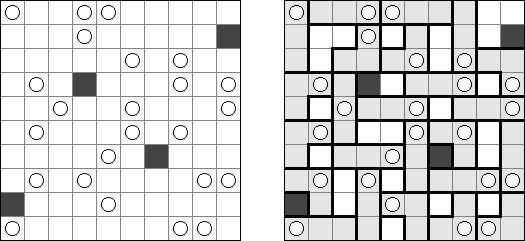
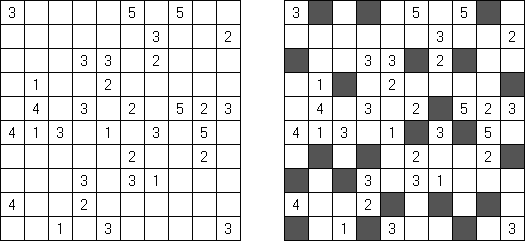
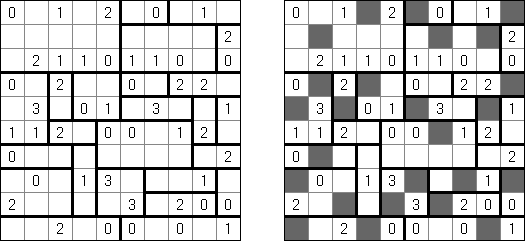
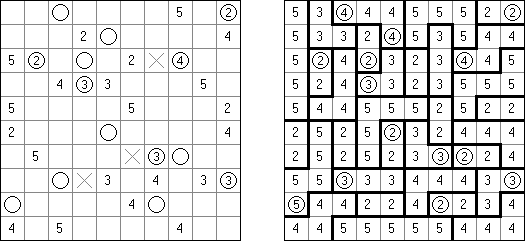
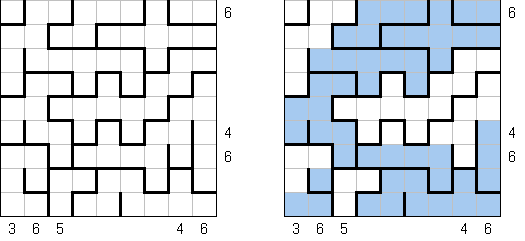
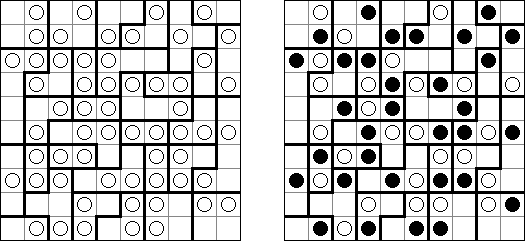
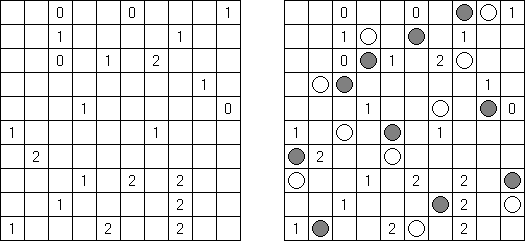
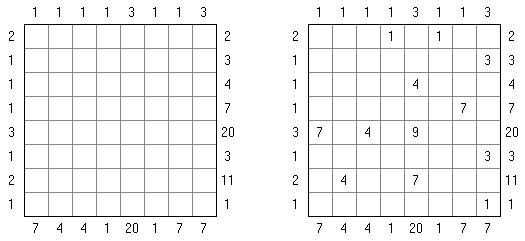
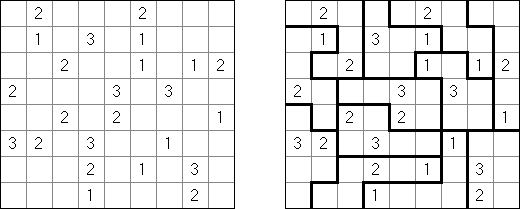
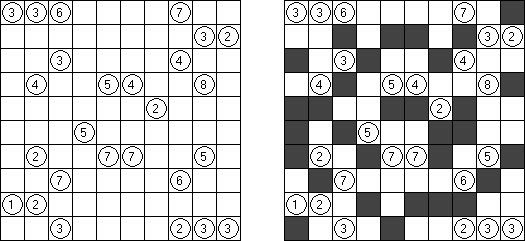
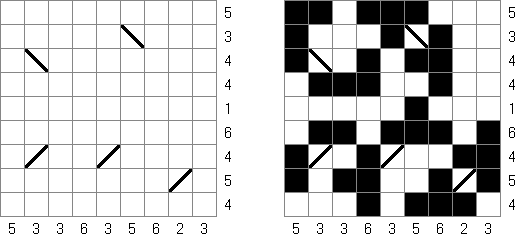
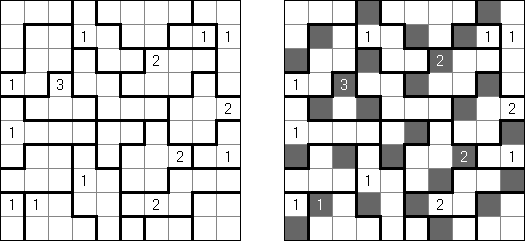
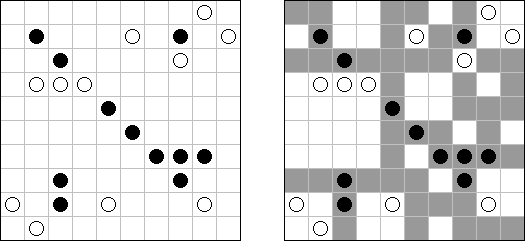
Fill-a-Pix (znane również jako "Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") – to łamigłówka z zaszyfrowanym obrazkiem. Każda liczba oznacza, ile pól wokół (łącznie z tą z liczbą) należy zamalować. Na przykład, jeśli w polu jest 0, to ani te pole, ani stykające się z nim nie będą zamalowani.

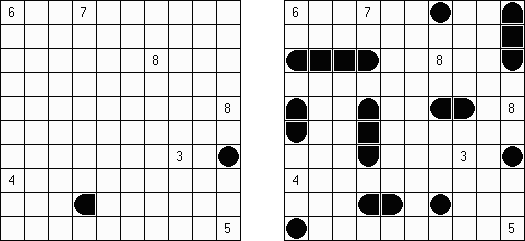
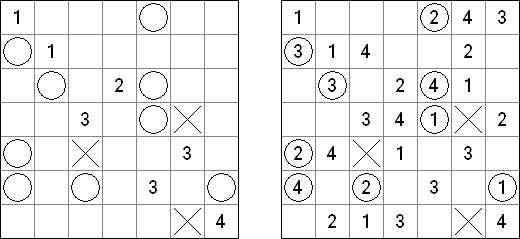
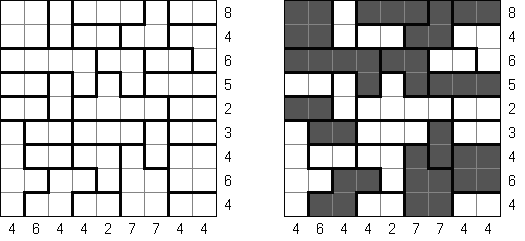
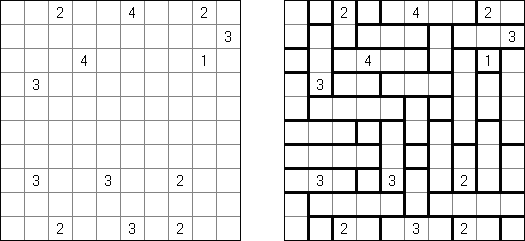
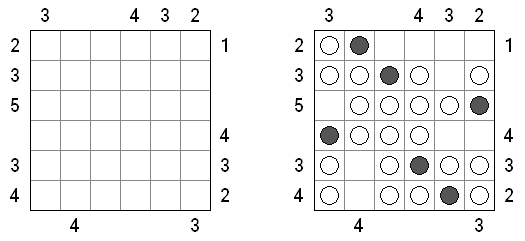
Battleships ("Okręty"; znany również jako "Solitaire Battleships", "Battleship Solitaire") – to znana gra w której należy rozmieścić "okręty" w taki sposób aby nie stykały się one ze sobą ani bokami, ani rogami. Liczby z prawej strony i u dołu pokazują, ile fragmentów okrętów ma być w rzędzie lub kolumnie.

Standardowy rozmiar pola - 10 x 10. Okręty są różnej wielkości. Każdy gracz posiada jeden czteromasztowiec z czterech kratek, dwa trójmasztowcy z trzech kratek, trzy dwumasztowcy z dwóch kratek i cztery jednomasztowce z jednej kratki. Czasem niektóre fragmenty okrętów są już ujawnione.

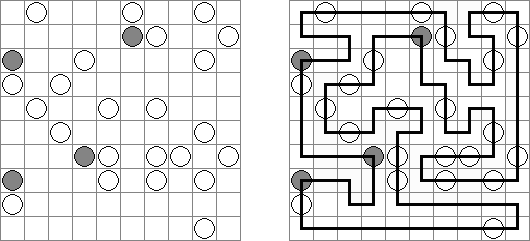
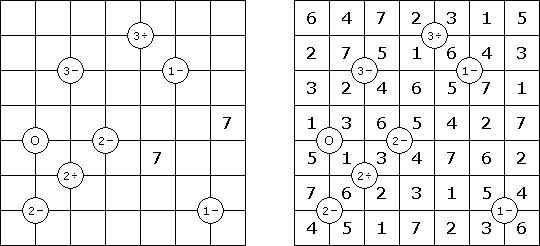
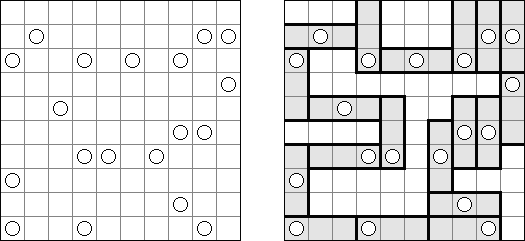
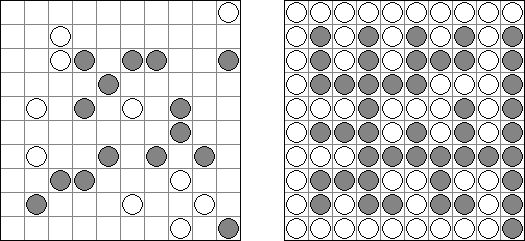
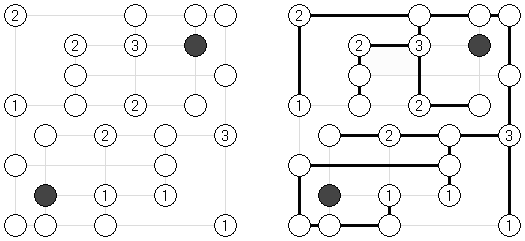
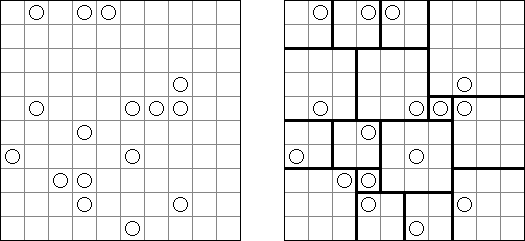
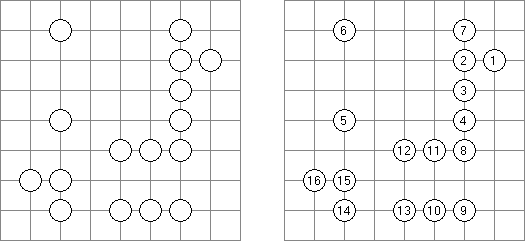
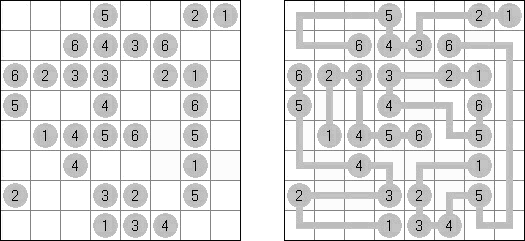
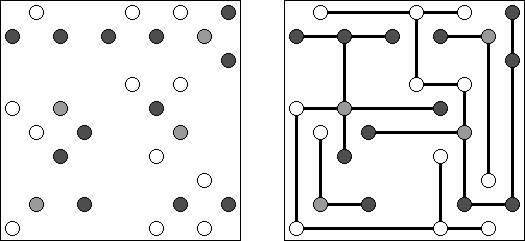
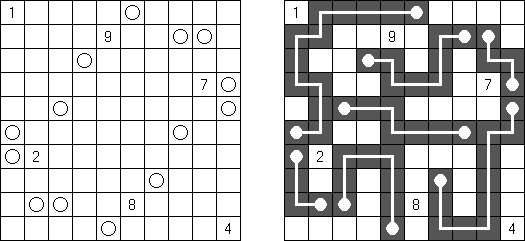
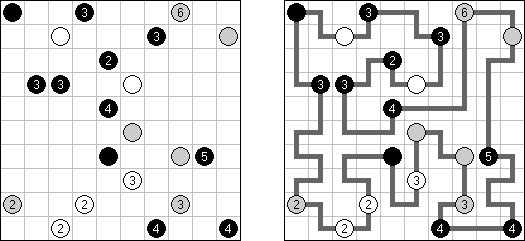
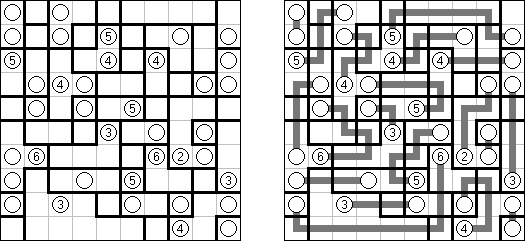
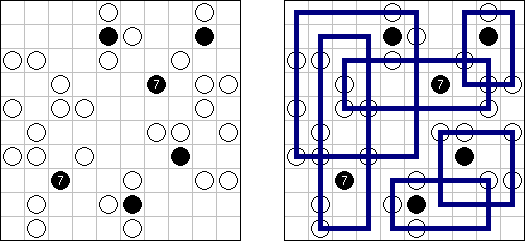
Hashiwokakero (z japońskiego "Hashi o kakero", znany również jako "Mosty", "Hashi", "Bridges", "Chopsticks" lub "Ai-Ki-Ai") – łamigłówka, w której należy połączyć koła z cyframi ("wyspy") za pomoćą tak zwanych mostów, które muszą być liniami prostymi. Liczba mostów wychodząca z jednej wyspy musi odpowiadać liczbie na niej. Żadna wyspa nie może być izolowana; mosty muszą być poprowadzone w taki sposób, aby z każdej wyspy można było dostać się do jakiejkolwiek innej wyspy.

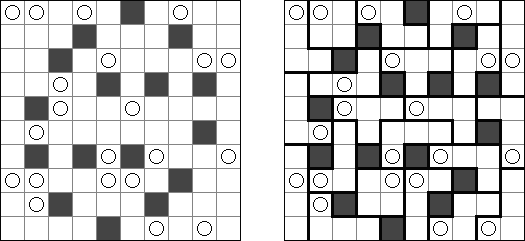
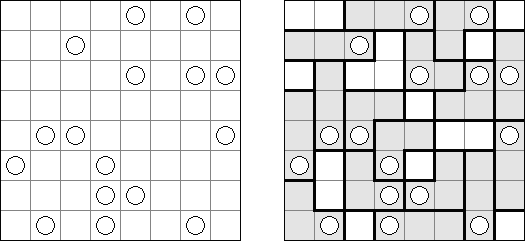
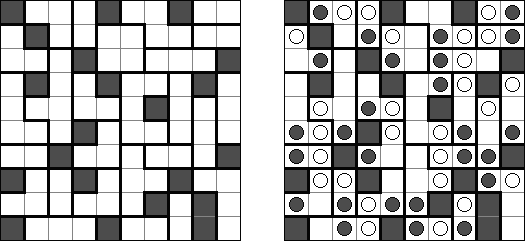
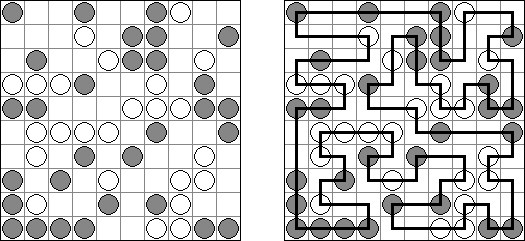
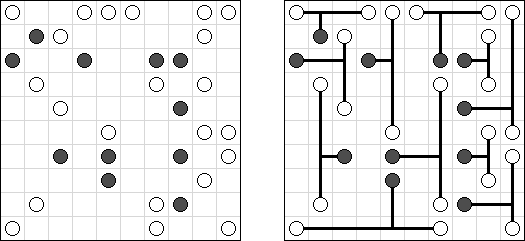
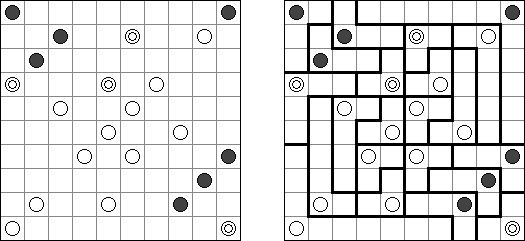
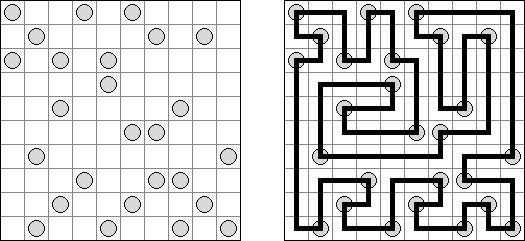
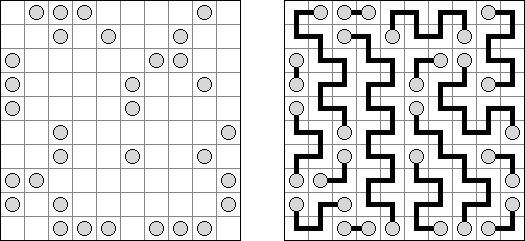
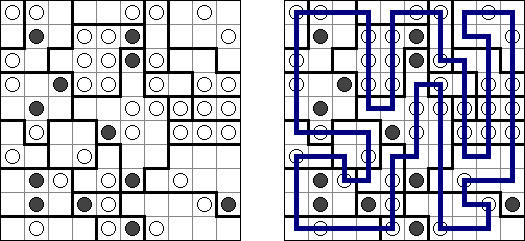
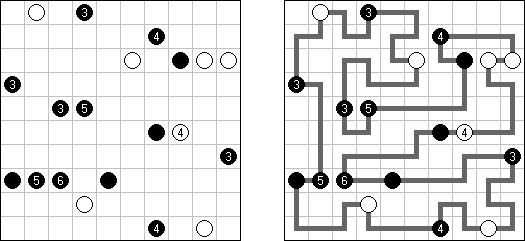
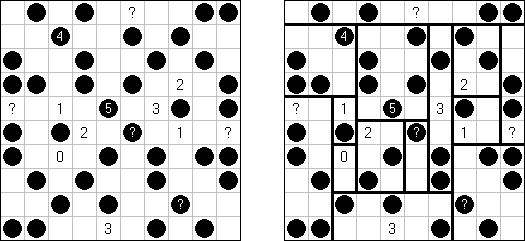
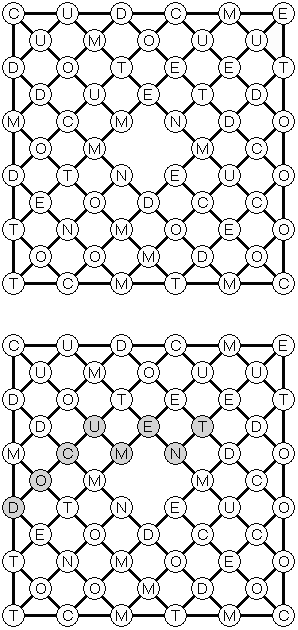
Masyu ("Koraliki"; znany również jako "Shiroshinju Kuroshinju", "White pearls and black pearls") – to logiczna łamigłówka, w której należy połączyć białe i czarne koła prostymi pionowymi i poziomymi odcinkami, aby sformować jednolitą zamkniętą linie bez skrzyżowań. Przez białe koła linia przechodzi prosto, ale powinna skręcić w poprzedniej lub następnej kratce (albo w dwóch tych kratkach). Gdy linia przecina czarne koło, ona musi skręcić o 90 stopni, przy tym w poprzedniej i następnej kratce skręty są wzbronione.

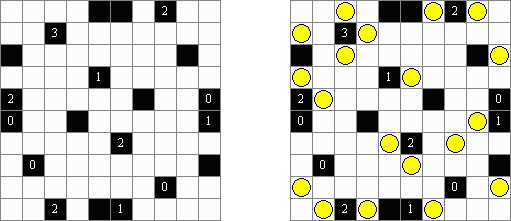
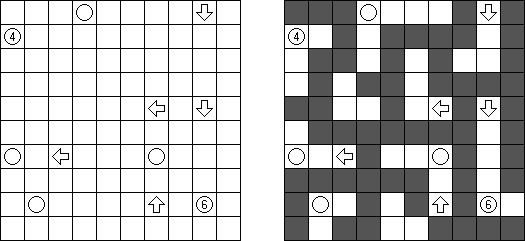
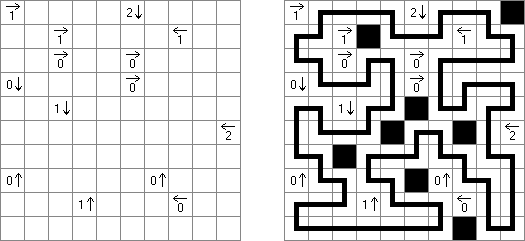
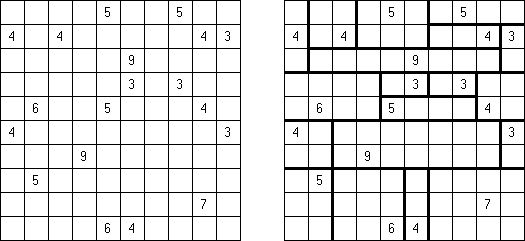
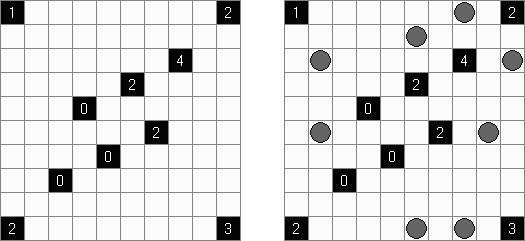
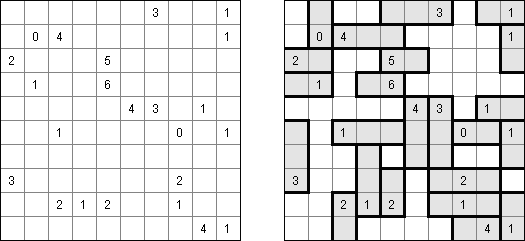
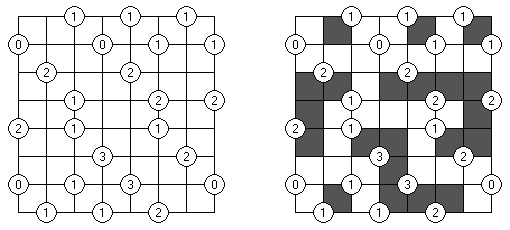
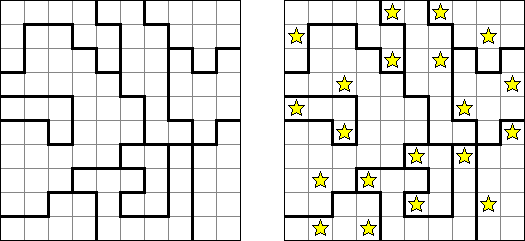
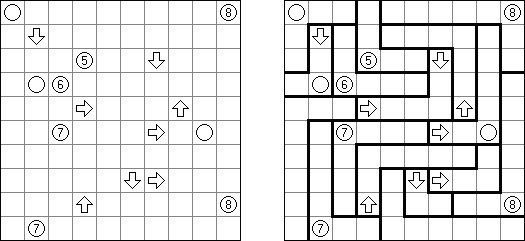
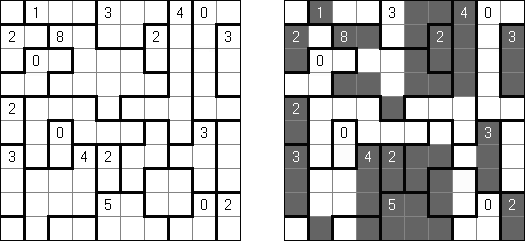
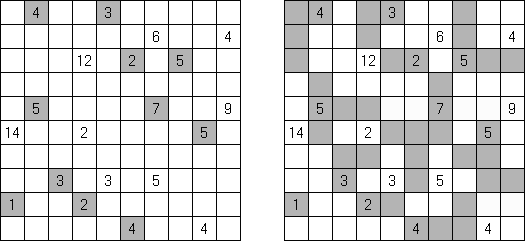
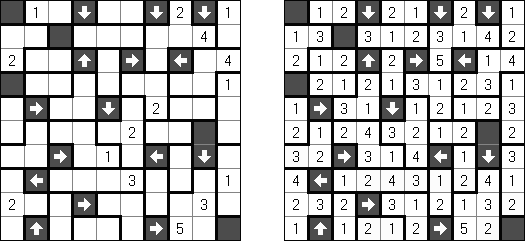
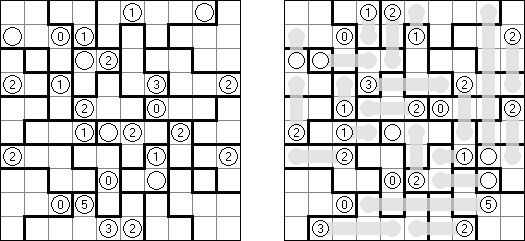
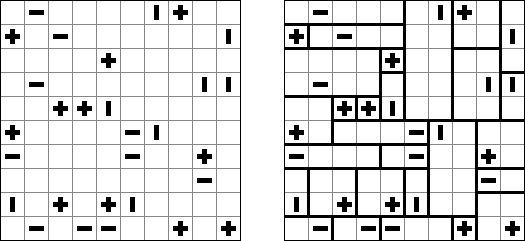
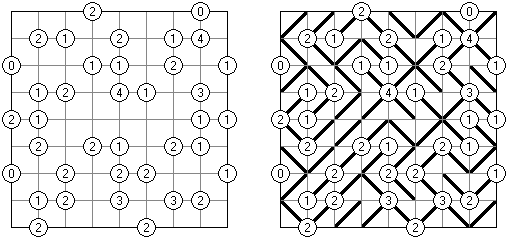
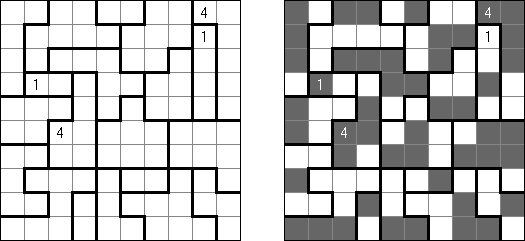
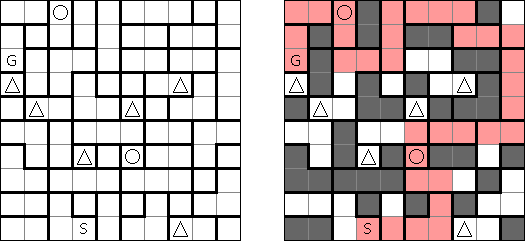
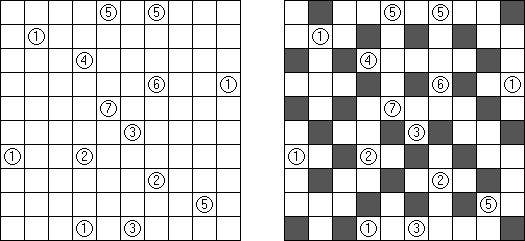
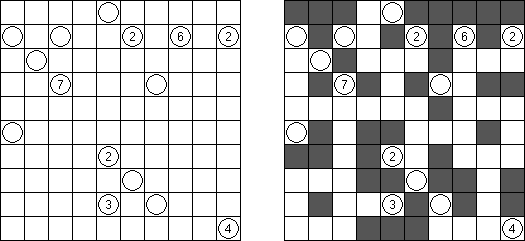
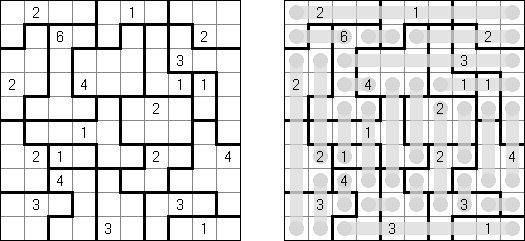
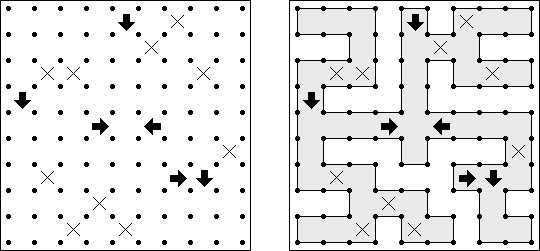
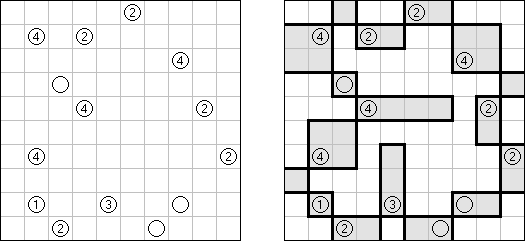
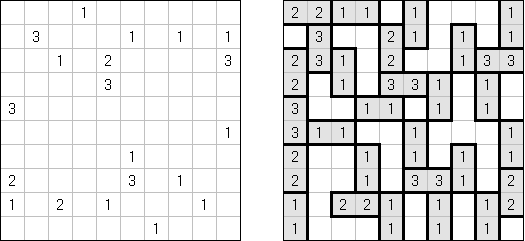
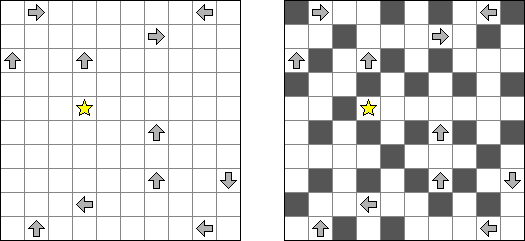
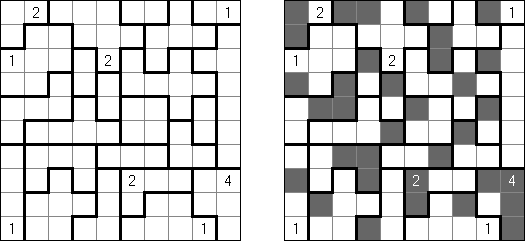
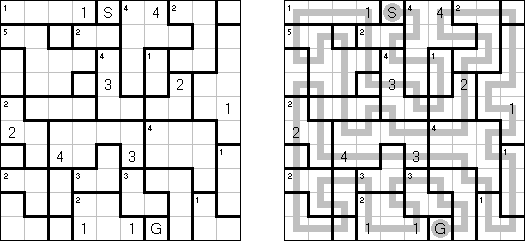
Akari ("Lampki"; znany również jako "Light Up", "Bijutsukan") – to logiczna łamigłówka. Płansza zawiera białe i czarne kratki; niektóre czarne kratki zawierają cyfry. Należy rozmieścić "żarówki" w białych kratkach w ten sposób, aby cała płansza została oświetlona, przy tym każda żarówka nie może "oświetlać" innej. Światło żarówki oświetla kratki w kierunku poziomym i pionowym, ale może zostać zablokowane przez czarną kratkę. Czarna kratka zawiera cyfry od 0 do 4, wskazując ile żarowek muszą być rozmieszczone obok (nie liczą sie żarówki, umieszczone ukośnie od tej czarnej kratki). Jeżeli kratka nie zawiera cyfry, obok niej znajdować się może jakakolwiek ilość żarówek.

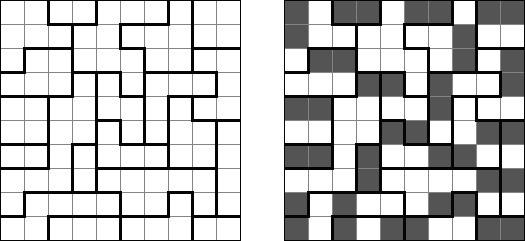
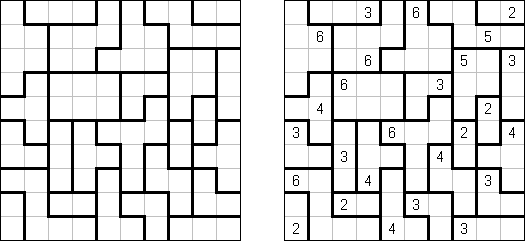
Fillomino ("Polyominous") – prostokątny pokratkowany diagram dowolnego rozmiaru; w niektórych kratkach znajdują się liczby. Należy podzielić płansze na bloki złożone z tylu kratek, jaką jest wartość tej liczby. Bloki tej samej wielkości nie mogą się stykać bokami. Kratki, które nie zawierają żadnej liczby też mogą być połączone w bloki.

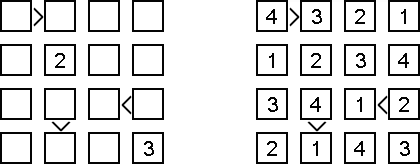
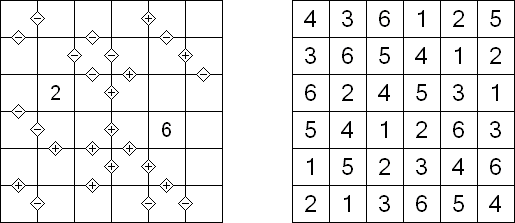
Futoshiki (z języka japońskiego, dosłownie "nie równa się"; znany również jako "Mniejsze większe", "Hutoshiki", "Unequal") – to logiczna łamigłówka liczbowa. W kwadratowym diagramie niektóre kratki zawierają już liczby; pomiędzy kratkami mogą znajdować się znaki "<" i ">", które pokazują stosunek między sąsiednimi liczbami. Należy wypełnić puste kratki, uważać przy tym, że każda liczba może znałeżć się w rzędzie lub kolumnie dokładnie raz.

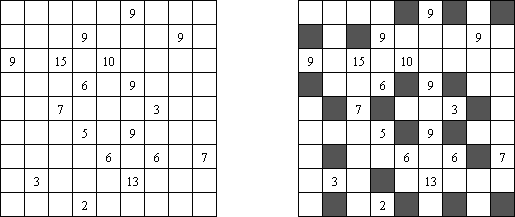
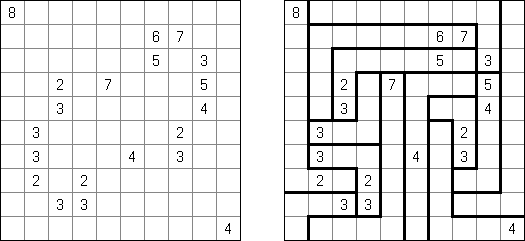
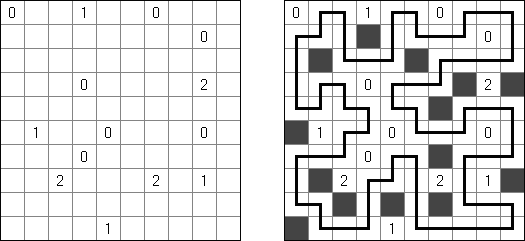
Kuromasu ("Wieże"; znany również jako "Kurodoko", "Where is Black Cells?") – prostokątny diagram z liczbami w niektórych polach. Należy zaczernić pola przestrzegając następujących warunków:

• każda liczba oznacza, ile białych pól "widać" z danego pola w kierunku pionowym i poziomym; "spojrzenie" zatrzymuje brzeg diagramu lub zaczernione pole;
• pola z liczbami są zawsze białe;
• czarne pola nie mogą się stykać się bokami;
• wszystkie białe pola tworżą jednolite białe pole.

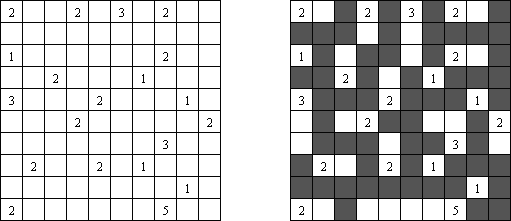
Nurikabe ("Wyspy"; znany również jako "Cell Structure", "Islands in the Stream") – logiczna łamigłówka liczbowa. W japońskiej mitologii istnieje potwór "nurikabie" w postaci wielkiej kamiennej ściany, ustawionej w poprzek drogi. Należy odtworzyć mapę z wyspami, przestrzegając następujących zasad:

• informację o każdej wyspie przedstawia liczba, co podaję ilość pól, z których składa się wyspa;
• jakiekolwiek dwie wyspy mogą się stykać tylko kątami;
• wszystkie wyspy zawierają w swoim opisie tylko jedną liczbe;
• między wyspami przepływa rzeka;
• wszystkie pola z rzeką muszą być połączone;
• mapa nie może zawierać żadnego kwadratu rozmiarem 2 x 2, wszystkie pola którego zawierają rzekę.

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

Tents ("Namioty"; znany również jako "Tents and Trees") – prostokątny diagram, niektóre kratki którego zawierają "drzewa". Należy rozmieścić obok drzew "namioty", przestrzegając następujących zasad:

• Liczba namiotów jest równa liczbie drzew.
• Każdy namiot styka się z "swoim" drzewem bokami, ale nie rogami. Jeśli spełniony zostanie ten warunek, lokalizacja w stosunku "cudzych" drzew nie ma znaczenia.
• Dwa namioty nie mogą znajdować się w sąsiednich kratkach, nawet wzdłuż przekątnej.
• Liczby po lewej stronie i u góry oznaczają, ile namiotów muszą znaleźć się w tym rzędzie lub kolumnie.

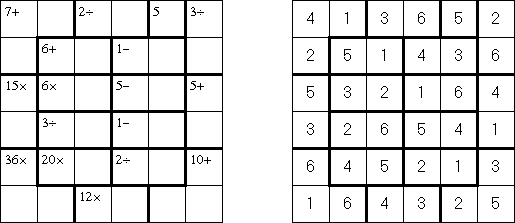
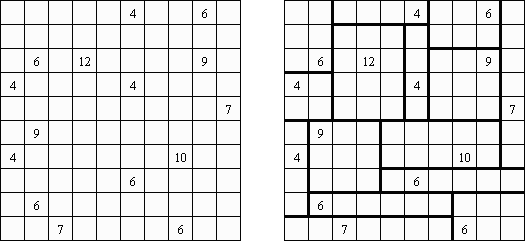
Calcudoku (znany również jako "KenKen", "KENKEN", "KenDoku", "Square Wisdom") – arytmetyczno-logiczna łamigłówka w której nałeży wypełnić diagram dostrzegając zasady, że każda liczba może znaleźć się w rzędzie lub kolumnie dokładnie raz. Każde z pól ma przypisane działanie arytmetyczne, liczby wewnątrz obwiedzionych grubszą linią błoków muszą spełniać to działanie. W odróżnieniu od Killer Sudoku, liczby wewnątrz bloku mogą powtarzać się.

Hidato ("Wąż królewski", "Hidoku"; w języku hebrajskim: "moja łamigłówka") – łamigłówka autorem której jest Gyora Benedek, matematyk izraelski. Diagram dowolnej formy (najczęściej to jest prostokąt lub kwadrat), składa się z pól, które należy wypełnić kolejnymi liczbami, które są połączeni pionowo, poziomo lub ukośnie. W każdej łamigłówce podane są najmniejsze i największe liczby. Także diagram zawiera inne liczby dla ułatwienia gry i zapewnienia jedyności rozwiązania.

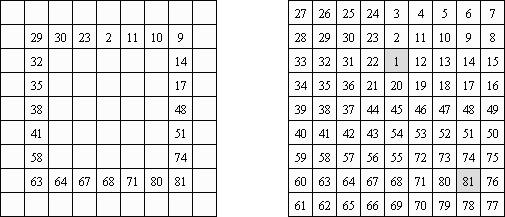
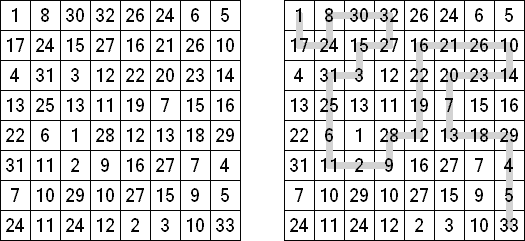
Numbrix ("Wąż prosty") – odmiana logicznej łamigłówki. Wygląda jak prostokątny diagram, w niektórych kratkach którego są zawarte liczby. Należy wypełnić puste kratki tak, aby wszystkie liczby zostały połączone kolejno w rzędzie lub kołumnie. Zabrania się połączenie ukośne.

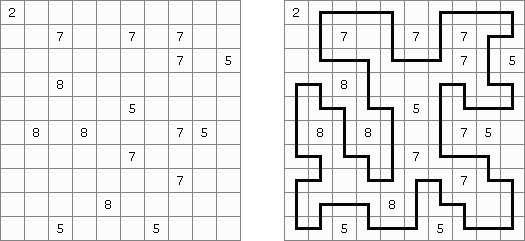
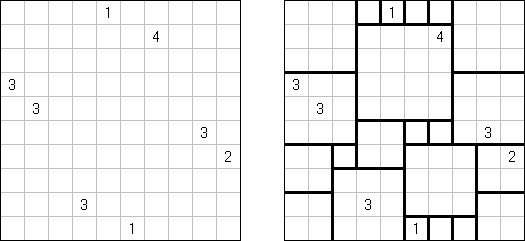
Shikaku ("Działki"; znany również jako "Divide by Squares", "Divide by Box", "Number Area") – to logiczna łamigłówka. Wygląda jak prostokątny diagram, niektóre go pola zawierają liczby. Nałeży poprowadzić linie i podzielić diagram na prostokątne i kwadratowe błoki w ten sposób, aby każdy błok zawierał dokładnie jedną liczbę, która wyznacza powierzchnię tego błoku.

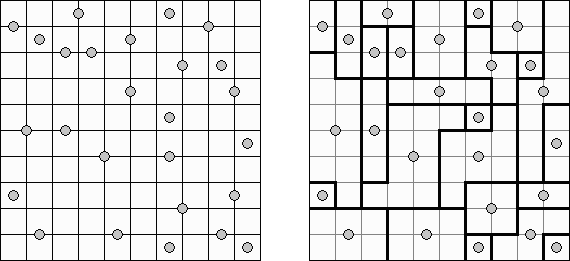
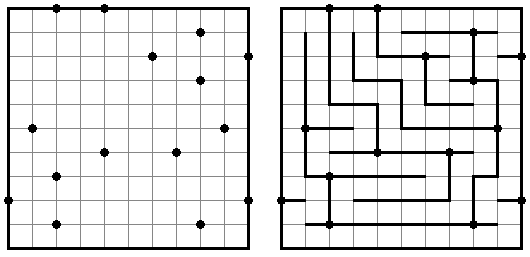
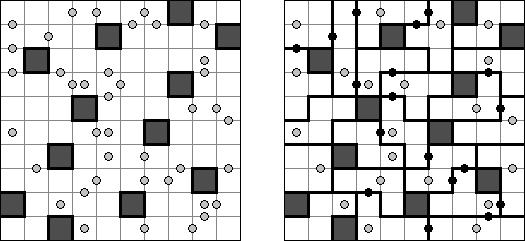
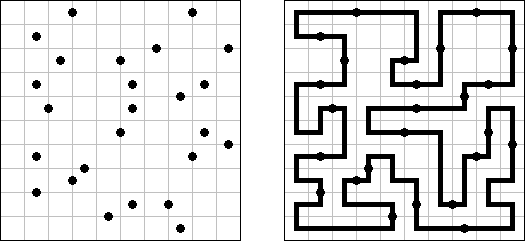
Galaxies ("Działki symetryczne"; znany również jako "Galaktyki", "Tentai Show") – logiczną łamigłówką geometryczną, która wygląda jak prostokątny diagram z kropkami. Należy podzielić płanszę na pola; każde pole musi zawierać tylko jedną kropke. Kropka znajduję się w centrum pola.

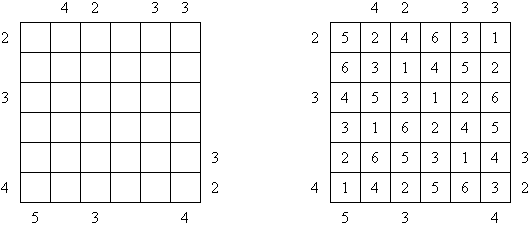
Skyscrapers ("Bloki", "Piramidy", "Wieżowce") – odmiana logicznej łamigłówki. Należy wypełnić kwadrat w taki sposób, aby w każdej linii i kolumnie znalazły się różne cyfry. Każda kratka wewnątrz kwadratu zawiera wieżowiec z ilością pięter, która jest równa liczbie w kratce. Kluczem są liczby umieszczone przy brzegu kwadratu, które oznaczają liczbę wieżowców widocznych w danym rzędzie patrząc na niego od strony, z której umieszczona jest liczba.

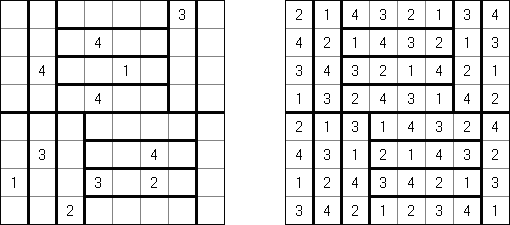
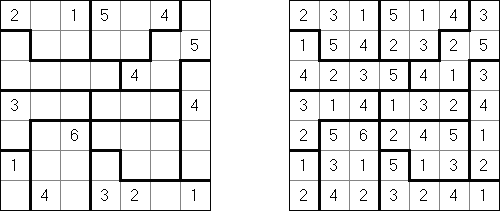
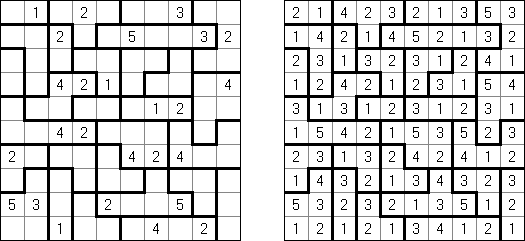
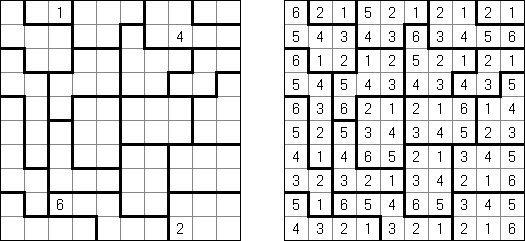
Hakyuu ("Obszary"; znany również jako "Ripple Effect", "Hakyuu Kouka", "Hakyukoka", "Seismic") – odmiana logicznej łamigłówki. Diagram podzielony jest grubymi liniami na bloki ("pokoje"); niektóre pola zawierają już liczby. Należy uzupełnić bloki liczbami w taki sposób, aby każdy blok zawierał cyfry od 1 do n (n – ilość kratek w bloku). Jeśli rząd czy kolumna zawiera dwie jednakowe cyfry, to one muszą być od siebie oddalone przynajmniej o podobną ilość pól. Na przykład, jeśli w kolumnie są dwa pola z liczbą 5, między nimi muszą znaleźć się przynajmniej pięć innych pól.

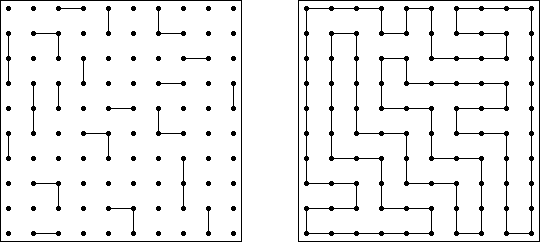
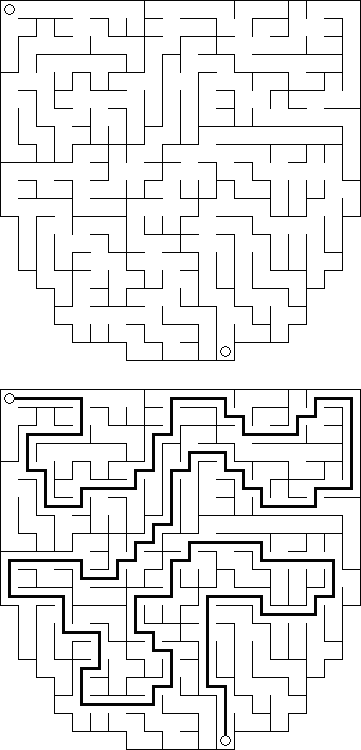
Grand Tour ("Pokropka bez cyfr") – logiczna łamigłówka, w której należy połączyć linią kropki na prostokątnej lub kwadratowej płanszy tak, aby sformować pojedynczą pętlę. Pętla nie może się przecinać. Aby zapewnić jedyność rozwiązania łamigłówki, niektóre kropki są już połączone.

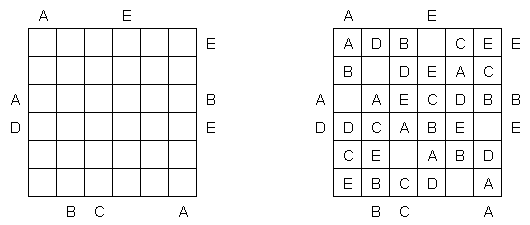
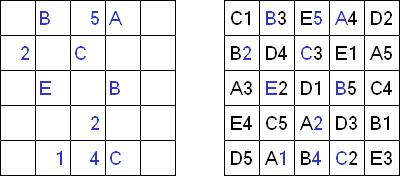
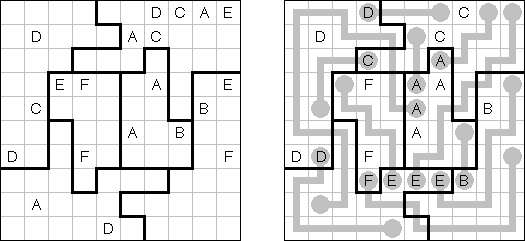
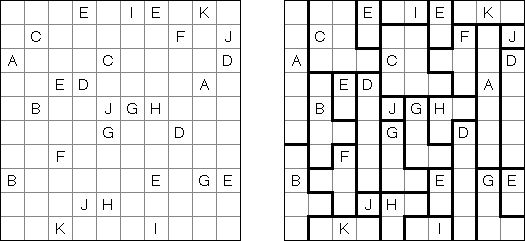
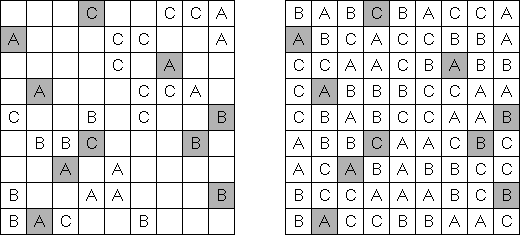
Easy as ABC ("ABC"; znany również jako "ABC End View", "Last Man Standing") – logiczna łamigłówka z literami. Należy uzupełnić kwadratową planszę literami (na przykład, od A do E), przy tym każda z nich może znałeżć się w rzędzie lub kolumnie dokładnie raz. Niektóre pola mogą zostać puśte. Litera poza płanszą wskazuje - jaka litera spotka się pierwszą w tym rzędzie (kolumnie).

Clouds ("Chmury"; znany również jako "Rain Clouds", "Radar") – to odmiana łamigłówki "Battleships". Na płanszy dowolnej formy należy rozmieścić prostokąty ("chmury") tak, aby nie stykały się one ze sobą w żaden sposób, nawet rogami. Liczby poza polem oznaczają ilość kratek, zajętych przez chmury. Ilość i rozmiar chmur nie podają się. Strony prostokątów nie mogą zawierać mniej dwóch kratek.

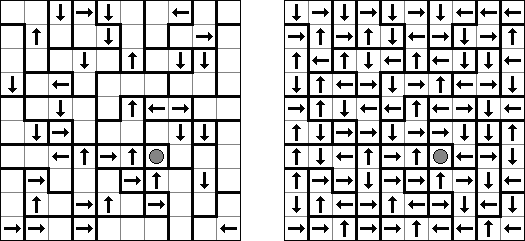
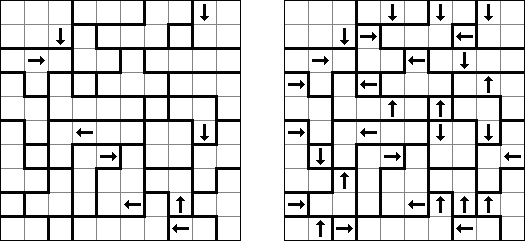
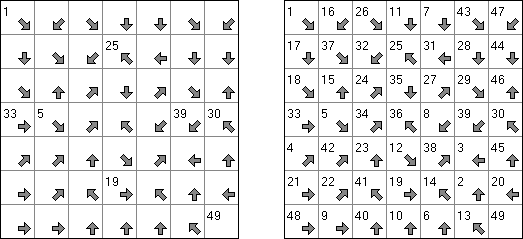
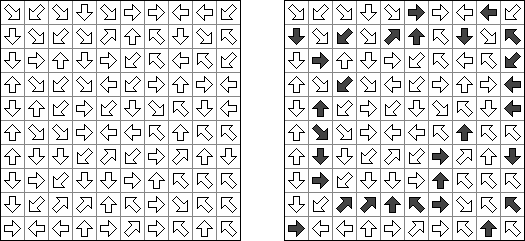
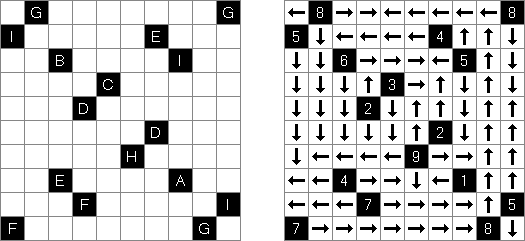
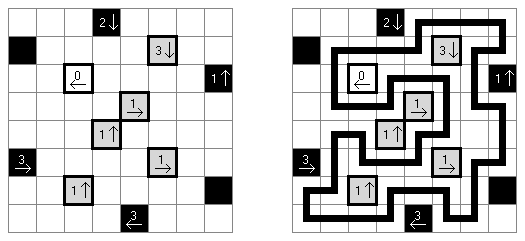
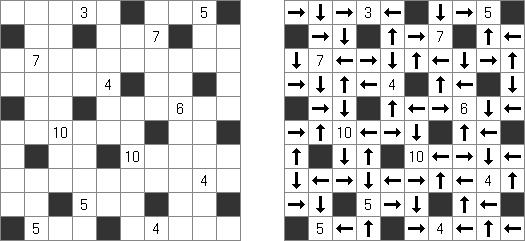
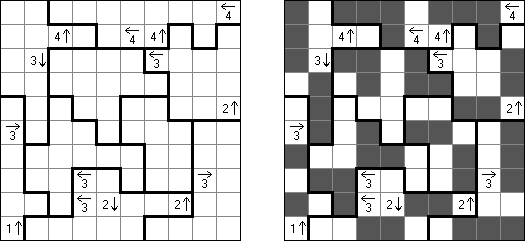
Yajilin ("Pętla i strzałki"; znany również jako "Arrow Ring", "Straight and Arrow") – logiczna kwadratowa lub prostokątna łamigłówka. Płansza zawiera pola ze strzałkami i liczbami; ta informacja potrzebna do rozmieszczenia zaczernionych pól. Celem jest zamknięta nie przecinająca się pętla, która nie może przejść przez pola ze strzałkami albo czarne pola. The grid may contain gray cells that can not be part of the loop.

• Liczby w polu oznaczają ilość czarnych pól w rzędzie czy kolumnie w kierunku strzałki. Pola ze strzałkami nie uważają się za czarne.
• Jeśli pole nie zawiera strzałki i nie jest czarne, to ono musi zawierać segment pętli.
• Liczby w polach wskazują ścisła liczbę czarnych pól. To znaczy, jeśli kratka zawiera "3" i strzałkę, wskazującą w lewo, to oznacza, że w rzędzie z lewej strony od takiej kratki są trzy czarnych pola.
• Czarne pola nie mogą się stykać.
• Na płanszy mogą być czarne pola, na które nie wskazuje żadna strzałka.

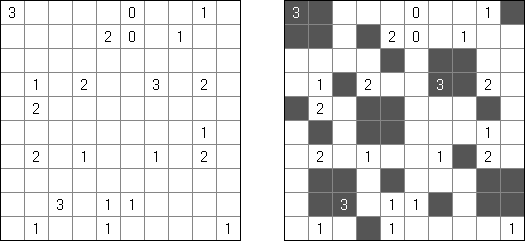
Minesweeper ("Saper") jedna z najpopularniejszych gier w systemie Microsoft Windows. Należy umieścić "miny" w polu; każda pole z liczbą podpowiada ile zaminowanych pól stykają się z tym polem. Jedne pole zawiera jedną mine. Pole z liczbą nigdy nie będzie polem z miną.

Minesweeper Battleships ("Saper + Okręty", "Battlemines") łączy w sobie dwie znane łamigłówki. Należy umieścić okręty w ten sposób, aby nie stykali się nawet rogami. W niektórych polach są już cyfry, które wskazują, ile fragmentów okrętów są wokół danego pola.

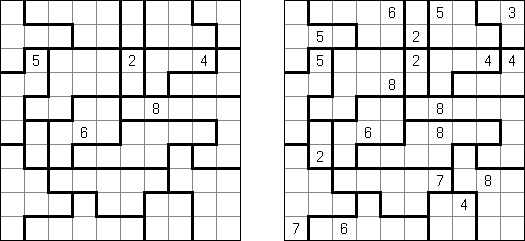
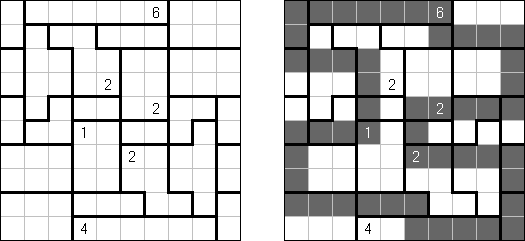
Heyawake ("Grządki") – logiczna łamigłówka. Wygląda jak prostokątny diagram, podzielony na bloki. Niektóre bloki zawierają już liczby, które wskazują ile czarnych pól musi zawierać blok. Bloki bez liczby mogą zawierać dowolną ilość czarnych pól.

• Czarne pola nie mogą się stykać bokami, tylko rogami.
• Wszystkie białe pola w bloku muszą tworzyć całość.
• Pozioma lub pionowa linia z białych pól może przechodzić przez co najwyżej dwa bloki.

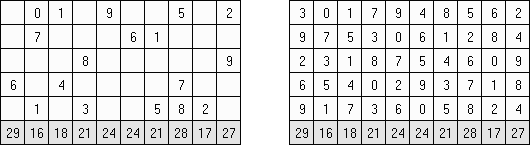
Tenner Grid (w Polsce znany jako "Liczbowóz", gdzie indziej "Od 1 do 10", "Zehnergitter", "Grid Ten") – prostokątny diagram 10 x 10. Należy uzupełnić diagram liczbami tak, aby każdy rząd zawierał cyfry od 0 do 9, które mogą się powtarzać w kolumnach. Liczba na dole diagramu oznacza sumę wszystkich cyfr w kolumnie. Liczby, które stykają się nawet rogami nie mogą być podobne.

Hundred ("Sto", "Setka") – kwadratowy diagram, każde pole którego zawiera cyfry. Należy dodać cyfry w polach tak, aby suma w każdym rzędzie i każdej kolumnie dorównywała 100.

Cross+A może rozwiązać diagramy 3 x 3 i 4 x 4.

Arrows ("Strzałki") – odmiana logicznej łamigłówki, która wygląda jak diagram prostokątny lub kwadratowy, wypełniony liczbami. Cel łamigłówki polega w ustawieniu strzałek poza granicami diagramu. Każda strzałka wskazuje chociażby na jedno pole z liczbą. Liczba oznacza ilość strzałek, wskazujących na pole.

Mathrax ("Ukośne działania") – odmiana logicznej łamigłówki. Należy wypełnić liczbami kwadratowy diagram, przy tym każda z nich może znałeżć się w rzędzie lub kolumnie dokładnie raz. Kwadrat może już zawierać niektóre liczby. Na skrzyżowaniach linii diagramu mogą być kola z dodatkowymi warunkami:

• Liczba i znak operacji arytmetycznej (dodawanie, odejmowanie, mnożenie i dzielenie) - liczba w kole zawiera wynik operacji arytmetycznej nad liczbami w polach wokół koła i stykających się rogami.
• Litera "E" - w polach wokół koła wszystkie cztery liczby parzyste ("E" – od angielskiego "even", parzysty).
• Litera "O" - w polach wokół koła wszystkie cztery liczby nieparzyste ("O" - od angielskiego "odd", nieparzysty).

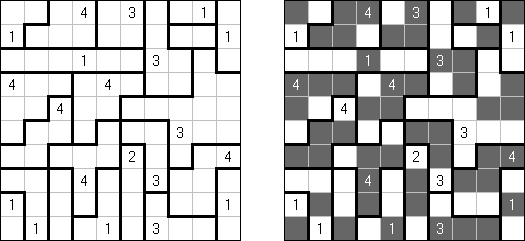
Str8ts ("Straights", w pokerze - pięć kolejnych kart w jednym kolorze; znany również jako "Kolejne cyfry") – logiczna łamigłówka, której autorem jest Jeff Widderich z Kanady. Kwadratowy diagram zawiera czarne i białe pola. Należy rozstawić liczby w białych polach w ten sposób, aby w odstępach między czarnymi polami utworzyły się zbióry kolejnych liczb (może być, na przykład: 2-1-3-4). W każdym rzędzie i w każdej kolumnie liczby w białych i czarnych polach nie mogą się powtarzać. Zezwala się wykorzystanie liczb od 1 do N, gdzie N - rozmiar strony diagramu. Liczby w czarnych polach nie wchodzą do zbióru kolejnych liczb.

Linesweeper ("Pętla sapera") – logiczna łamigłówka, podobna do "Sapera" ("Minesweeper"). Wygląda jak kwadratowy albo prostokątny diafram; w niektórych polach są zawarte liczby (od 0 do 8). Należy poprowadzić zamkniętą linię przez pola; linia nie powinna się przecinać albo przechodzić przez pola z liczbami. Liczba w polu wskazuje, przez ile pól, rozmieszczonych wokół pola z liczbą, przechodzi linia.

Binairo ("Zera i jedynki"; znany również jako "Binary Puzzle", "Takuzu", "Tohu wa Vohu") – logiczna łamigłówka z wykorzystaniem cyfr "0" i "1". Prostokątny albo kwadratowy diagram należy wypełnić cyframi zgodnie następujących zasad:

• każdy rząd i każda kolumna zawierają tyle samo zer i jedynek (lub o jedną liczbę więcej dla diagramu z nieparzystą ilościa pól);
• trzy kolejne cyfry nie mogą być jednakowe;
• nie może być dwóch kolumn, ani dwóch rządów z identycznym układem cyfr.

Walls ("Ściany") – logiczna łamigłówka autorstwa japończyka Naoki Inaba. Należy rozstawić w białych polach poziome i pionowe odcinki tak, by sumaryczna długość wszystkich odcinków wychodzących z czarnego pola odpowiadała liczbie w tym polu.

Dominosa ("Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") – logiczna łamigłówka z kostkami domino. Na pole podane są liczby; należy odtworzyć granicy między kostkami domino.

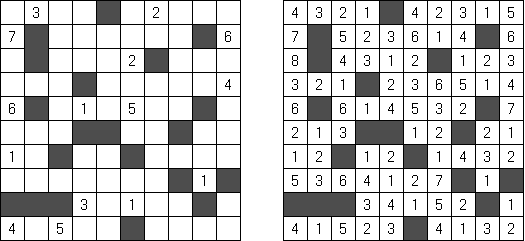
Patchwork ("Parkiet"; znany również jako "Skrawki", "Tatami") – kwadratowy diagram, podzielony na jednakowe bloki. Należy uzupełnić każdy blok liczbami od 1 do liczby, równej ilości pól w bloku. Każdy rząd i każda kolumna muszą zawierać jednakową ilość cyfr. Sąsiednie pola stykające się bokami nie muszą zawierać podobne cyfry.

W niektórych łamigłówkach są wykorzystywane litery. Cross+A może rozwiązywać łamigłówki z cyframi i literami.

Knossos (miejscowość na greckiej wyspie Krecie, słynna z ruin pałacu Minosa, zwanego labiryntem kreteńskim) – prostokątny lub kwadratowy diagram liczbowy. Należy podzielić diagram na bloki tak, aby w każdym znalazłaby się pojedyncza liczba, która jest równa długości obwodu bloku.

Rekuto ("Wymiary", "Recto") – logiczna łamigłówka kwadratowa lub prostokątna. Niektóre pola zawierają już liczby. Należy poprowadzić linie i rozdzielić diagram na prostokątne i kwadratowe bloki w ten sposób, aby każdy blok zawierał tylko jedną liczbę, równą sumie szerokości i wysokości bloku.

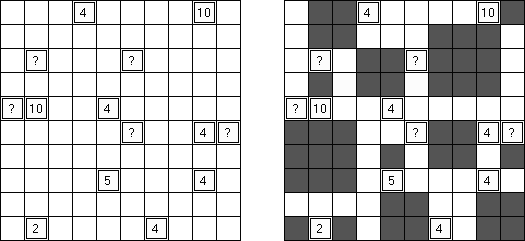
Neighbours ("Państwa", "Sąsiedzi") – to logiczna łamigłówka, która wygląda jak dowolny diagram. W niktórych polach są zawarte liczby albo pytajniki. Należy podzielić diagram na bloki z jednakową ilością kratek. Każdy blok musi zawierać tylko jedną kratkę z liczbą (albo z pytajnikiem); ta liczba wskazuje, ile "sąsiadów" ma ten blok. Dwa bloki są uważane za sąsiednie jeśli posiadają wspólną granicę. Jeśli blok zawiera kratkę z pytajnikiem, to może posiadać dowolną ilość "sąsiadów".

Four Winds ("Cztery wiatry", "Promienie", "Line Game") – logiczna łamigłówka, która wygląda jak kwadratowy albo prostokątny diagram z czarnymi i białymi polami. Należy poprowadzić proste linie wychodzące z czarnych pól przez wszystkie białe pola. Liczba w czarnej klatce oznacza, ile białych pól zajmują linie, połączone z tym czarnym polem. Linie nie mogą się przecinać.

Shakashaka ("Ukryte prostokąty"; znany również jako "Proof of Quilt") – logiczna kwadratowa lub prostokątna łamigłówka. Diagram zawiera białe i czarne pola; w niektórych czarnych polach są już cyfry (od 0 do 4). Należy rozstawić w białych polach czarne trójkąty tak, aby sformować prostokątne i kwadratowe białe obszary. Niektóre białe pola mogą być puste. Obszary mogą być rozmieszczone pionowo, poziomo albo ukośnie, nie mogą mieć wspólnych stron. Cyfra w czarnym polu oznacza, ile trójkątów stykają się bokami z polem z liczbą.

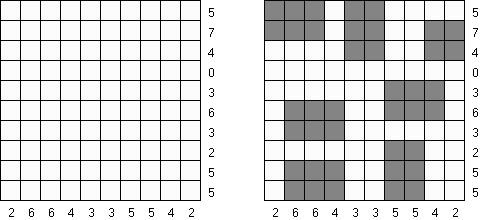
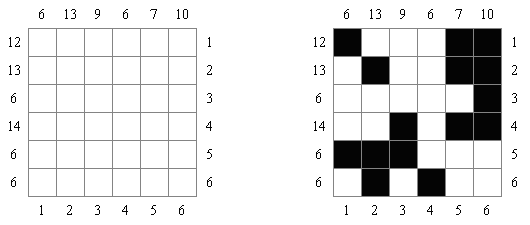
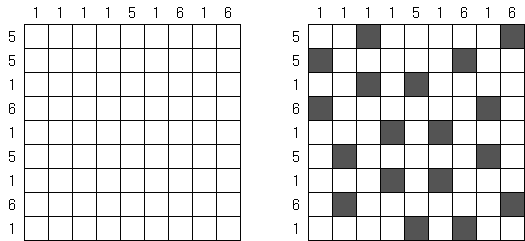
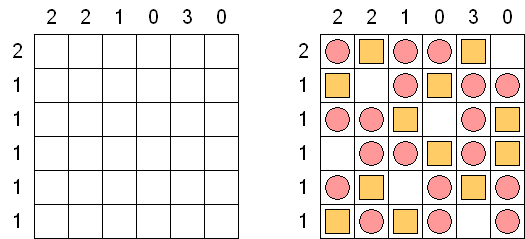
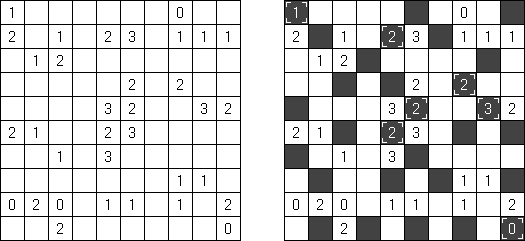
Kakurasu (znany również jako "Index Sums") – łamigłówka kwadratowa albo prostokątna, w której należy rozstawić czarne i białe pola. Na gorze podane są sumy wartosci czarnych pól w kolumnach (wartosci po prawej). Z lewej strony – wartosci dla rzędów (wartosci na dole). Należy zamalowac pola w taki sposób, aby wszystkie sumy się zgadzaly. Wartość czarnego pola w pierwszym rzędzie lub kolumnie równa 1, w drugim rzędzie lub kolumnie - 2, itp.

Mochikoro ("Tratwy"; znany również jako "Mochinuri") – prostokątny albo kwadratowy diagram z liczbami. Należy rozmieścić białe i czarne pola w taki sposób, aby utworzyli się prostokątne lub kwadratowe "wyspy" z białych pól.

• Jedna biała "wyspa" może zawierać jedne pole z liczbą; liczba oznacza ilość białych pól, z których składa "wyspa".
• Są "wyspy" bez ujawnionej liczby.
• "Wyspy" są prostokątami i stykają się rogami w taki sposób, że wszystkie są ze sobą połączone.
• Pola czarne nigdzie nie tworzą kwadratu 2 x 2.

Seethrough ("Drzwi"; znany również jako "Doors", "Open Office") – logiczna łamigłówka kwadratowa lub prostokątna, w której każda komórka oznacza "pokój". Należy zamknąć albo otworzyć "drzwi" pokojów. Przez otwarte drzwi widać inny pokój lub kilka pokojów. Komórka z liczbą oznacza, ile komórek widać z niej, z wyjątkiem samej siebie. Z każdej komórki musi być droga do jakiejkolwiek innej.

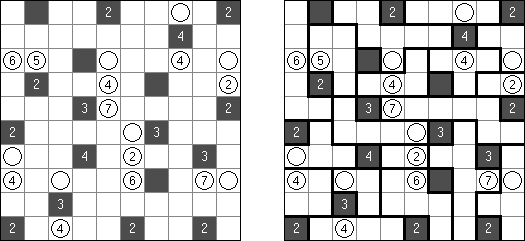
Lighthouses ("Latarnie morskie") – logiczna łamigłówka, zawierająca czarne pola z liczbami ("latarnie morskie"). Liczba oznacza, ile pól zajmowanych przez okręty jest przez daną latarnię oświetlonych. Latarnia morska oświetla okręty w jednym rzędzie albo kolumnie, nawet gdy między nią a okrętem są inne okręty albo latarnie. Każdy okręt oświetlony jest przez co najmniej jedną latarnię. Okręty nie mogą bezpośrednio sąsiadować z latarniami ani z sobą (w tym stykać się rogami).

Lighthouse Battleships połaczenie łamigłówek "Latarnie morskie" i "Okręty". Wygląda jak kwadratowa lub prostokątna płansza, która zawiera "latarnie" – kratki z liczbami. Liczba oznacza sumę fragmentów okrętów w wierszu i kołumnie z latarnią. Kratka z liczbą nie może zawierać fragment okrętu. Okręty nie mogą stykać się z sobą ani z latarniami nawet rogami.

Tapa ("Wąż sapera") – łamigłówka której autorem jest Serkan Yürekli z Turcji. W kwadratowym lub prostokątnym diagramie część pustych pól należy zaczernić tak, aby czarne pola utworzyły spójną całość (wielokąt) przy tym muszą spełniać następujące warunki:

• Czarne pola stykają się bokami.
• Czarna całość nie może obejmować kwadratów 2 x 2.
• Niektóre pola zawierają liczby lub pytajniki; takie pola zostają białe.
• Każda liczba oznacza spójną grupe pól wokół pola z liczbą, którą należy zaczernić; pomiędzy takimi grupami musi być co najmniej jedno pole puste.
• Pytajnik oznacza liczbe większą od zera.
• Rozmieszczenie liczb w polu nie ma znaczenia.

Fobidoshi ("Max 3", "Forbidden Four") – logiczna łamigłówka autorstwa japończyka Naoki Inaba. Wygląda jak prostokątny albo kwadratowy diagram, w niktórych komórkach którego są rozmieszczone koła. Należy rozstawić w pustych kratkach koła tak, aby wszystkie koła stykali się bokami. Linia pozioma albo pionowa nie może zawierać cztery kolejne koła.

Island ("Wyspa"; znany również jako "Tents Island", "Airando") – logiczna łamigłówka autorstwa japończyka Naoki Inaba. Wygląda jak diagram z liczbami. Należy zaczernić komórki tak, aby pozostałe białe komórki sformowali jeden obszar (wyspę). Komórki z liczbami są częścią wyspy. Liczba wskazuje, ile białych komórek bez liczb można przejść w kierunku poziomym i pionowym do następnej komórki z liczbą.

Dominion – łamigłówka logiczna stworzona przez Naoki Inaba (Japonia). Należy zaczernić pola, przestrzegając następujących zasad:

• Czarne pola można dodawać tylko parami, tzn. każde dwa nowe czarne pola muszą stykać się bokami (takie pary nazywają "kostkami domino").
• Kostki domino mogą stykać się tylko rogami.
• Pola z literami zostają białe.
• Czarne pola rozdzielają diagram na białe obszary.
• Pola z podobną literą należą jednego obszaru.
• Biały obszar musi zawierać co najmniej jedno pole z literą.

Tren – łamigłówka logiczna autorstwa japończyka Shinichi Aoki. W języku japońskim to oznacza "parking" (każdy blok - to samochód, a diagram - parking). Łamigłówka wygląda jak prostokąt lub kwadrat, z liczbami w niktórych polach. Należy rozmieścić na płanszy bloki 1 x 2 i 1 x 3. Każda liczba – to część jednego bloku. Ta liczba wskazuje, o jaką ilość pól można zruszyć blok. Blok można posuwać tylko w kierunku jego krótkiej strony.

No Four in a Row ("Trzy w jednej linii") – diagram dowolnego kształtu. W niektórych kratkach są iksy i zera. Należy uzupełnić pozostałe kratki tak, aby poziomo, pionowo i ukośnie znalazło się kolejno nie więcej niż trzy podobne elementy.

Corral ("Bag", "Cave") – prostokątny lub kwadratowy diagram z liczbami. Należy sformować pojedynczą pętlę naokoło liczb. Kratka z liczbą oznacza ilość kratek, które widoczne z niej w kierunku poziomym i pionowym wewnątrz pętli, łącznie z tą kratką.

Foseruzu ("Cztery klatki", "Four Cells") – logiczna łamigłówka, wygląda jak prostokątny diagram z liczbami w pewnych komórkach. Należy podzielić diagram na bloki z czterech komórek. Liczba oznacza, ile stron komórki zawierają elementy granic pomiędzy blokami (łącznie z zewnętrzną granicą diagramu). Blok może zawierać dowolna ilość liczb (lub nie zawierać żadnej).

Faibuseruzu ("Pięć klatek", "Five Cells", "Solomon's Keep"): łamigłówka podobna do Foseruzu, lecz diagram należy podzielić na bloki z 5 komórek.

Sutoreto ("Sutoretokurosu" - tak brzmi w języku japońskim angielska nazwa "Straight Cross") – logiczna łamigłówka autorstwa Naoki Inaba z Japonii. Łamigłówka wygląda jak prostokątny lub kwadratowy diagram z białymi i czarnymi polami. Niektóre białe pola zawierają liczby. Należy wypełnić liczbami pozostałe białe pola tak, aby pomiędzy czarnymi polami w linii poziomej i pionowej znalazły by się komplety kolejnych liczb (na przykład, 2-3-4 albo 5-4-7-6).

Renban – kwadratowy diagram, podzielony na bloki dowolnego rozmiaru i wyglądu. Należy wypełnić diagram liczbami. W każdej linii, każdej kolumnie i każdym bloku każda liczba może znałeżć się dokładnie raz. Liczby wewnątrz bloku są zbiórami kolejnych liczb, ale nie koniecznie od największego do najmniejszego lub odwrotnie (na przykład: 5-3-4).

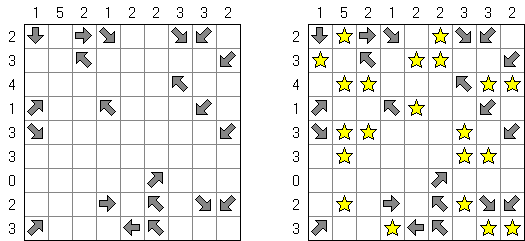
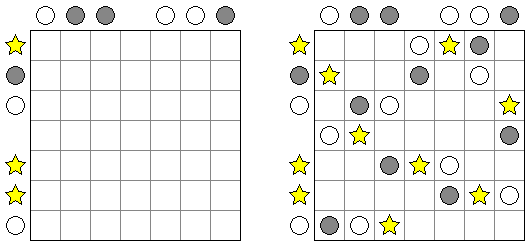
Buraitoraito (zniekształcona przez japońską wymowę angielska nazwa "Bright Light") – łamigłówka autorstwa Naoki Inaba z Japonii. Wygląda jak kwadratowy lub prostokątny diagram z białymi i czarnymi polami. Należy wypełnić białe pola gwiazdami w ten sposób, aby każda liczba w czarnym polu odpowiadała ilości gwiazd, widzianych z tego pola w kierunku poziomym i pionowym. "Spojrzenie" zatrzymuje brzeg diagramu lub zaczernione pole.

Irasuto ("Illustration") – logiczna łamigłówka autorstwa Naoki Inaba z Japonii. Wygląda jak prostokątny lub kwadratowy diagram z białymi i czarnymi polami. W niektórych polach są liczby. Należy rozstawić czarne i białe pola, przestrzegając następujących zasad:

• Liczba w białym polu oznacza, ile białych pól "widać" z tego pola w kierunku pionowym i poziomym. "Spojrzenie" zatrzymuje zaczernione pole lub białe pole z liczbą.
• Liczba w czarnym polu oznacza, ile czarnych pól "widać" z tego pola w kierunku pionowym i poziomym. "Spojrzenie" zatrzymuje białe pole lub zaczernione pole z liczbą.

Suguru ("Number Blocks") – logiczna łamigłówka autorstwa Naoki Inaba z Japonii. Wygląda jak kwadratowy lub prostokątny diagram, podzielony na bloki. Należy wypełnić wszystkie pola liczbami tak, aby każdy blok zawierał liczby od 1 do N (N - ilość pól w bloku). Pola z podobnymi liczbami nie mogą stykać się poziomo, pionowo lub ukośnie.

Trinudo – prostokątna pokratkowana łamigłówka logiczna z liczbami w niektórych kratkach. Należy podzielić płanszę na bloki z jednej, dwóch lub trzech kratek. Jednakowe bloki nie mogą stykać się poziomo lub pionowo. Każda liczba wskazuję ile kratek zawiera blok z tą liczbą.

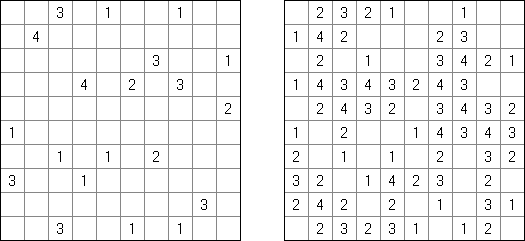
Creek ("Kuriku") – kwadratowa lub prostokątna łamigłówka logiczna; na przecięciach linii są kola z liczbami od 0 do 4. Liczba oznacza ilość czarnych kratek wokół kola. Należy rozmieścić białe i czarne kratki w taki sposób, aby wszyskie białe pola stykali się pionowo lub poziomo.

Gappy - łamigłówka logiczna, wygląda jak kwadratowy diagram. Należy umieścić czarne komórki w taki sposób, aby w każdym wierszu i każdej kolumnie znalezli się dwie czarne komórki. Czarne komórki nie mogą stykać się ze sobą ani bokami, ani rogami. Liczby umieszczone przy brzegu diagramu oznaczają ile komórek białych znajduje się między czarnymi komórkami w wierszu lub kolumnie.

Norinori - rodzaj logicznej łamigłówki. Wygląda jak kwadratowy lub prostokątny diagram podzielony na bloki o dowolnym kształcie. Należy w każdym bloku zaczernić dwie komórki. Czarne komórki muszą tworzyć bloki 2 x 1 lub 1 x 2 (klocki domina), bez względu na granice bloków. Dwa czarne bloki nie mogą stykać się bokami (ale mogą stykać się rogami).

Yonmasu ("Yonmasubunkatsu") - łamigłówka logiczna autorstwa japończyka Naoki Inaba. Wygląda jak kwadratowy lub prostokątny diagram. Niektóre pola zawierają koła. Należy rozdzielić diagram na bloki z czterech komórek w taki sposób, aby każdy blok zawierał jedne koło.

Bricks consists of a square grid. The aim is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Every brick contains an odd number and an even number.

Number Chain is a logic puzzle invented by Leonid Mochalov (Russia). A rectangular or square grid contains numbers from 1 to N in cells. The aim is to draw a single continuous line from the upper left corner to the lower right corner. The line includes each number from 1 to N exactly once.

Kapetto ("Settokapetto" - zniekształcona przez japońską wymowę angielska nazwa "Set Carpets") - łamigłówka wymyślona przez Naoki Inaba z Japonii. Wygląda jak kwadratowy lub prostokątny diagram, z komórkami, które zawierają liczby. Należy umieścić prostokątne bloki tak, aby każdy zawierał jedna liczbe.Liczba oznacza ilość komórek w bloku. Diagram może zawierać komórki, które nie należą do żadnego bloku.

Renkatsu – łamigłówka logiczna autorstwa japończyka Naoki Inaba. Wygląda jak kwadratowa lub prostokątna płansza wypełniona liczbami. Należy rozdzielić płanszę na bloki w taki sposób aby każdy zawierał liczby od 1 doN, N – rozmiar bloku.

Eulero ("Graeco-Latin Square", "Euler Square") is a puzzle with letters and digits. The goal is to fill in the grid with symbols according to the following rules:

• Each cell contains one letter and one digit.
• Every row and every column contains each letter and each digit exactly once.
• No two cells contain the same pair of symbols.

Anraikumozaiku (zniekształcona przez japońską wymowę angielska nazwa "Unlike Mosaic") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to divide the grid into rectangular regions. Each region contains one circle. Black cells do not belong to any region. Regions of the same size must not share an edge.

Kurotto (from Japanese, literally "black units") is a logic puzzle published by Nikoli. The task consists of a grid, with circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• Cells with circles can not be blacken.
• Black cells form orthogonally contiguous areas.
• A number in a circle indicates the total number of black cells in areas orthogonally neighboring the circled cell.
• Cells with empty circles may have any number of black cells around them.

Tasukuea (from Japanese, literally "find squares") is a type of logic puzzles. It is played on a rectangular or square grid with numbers or question signs in some cells. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers or question signs can not be blacken.
• Black cells form square areas, that must not be orthogonally adjacent.
• A number in a circle indicates the total number of black cells in areas orthogonally neighboring the numbered cell.
• A cell with a question sign must have at least one adjacent black cell.
• All the white cells must be connected horizontally or vertically.

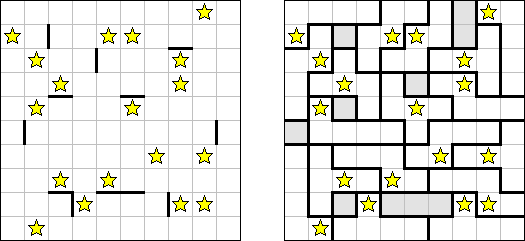
Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.

Araf (from Turkish, literally "purgatory"; original Japanese name - "Aidabeya") is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.

Kabingurodo (zniekształcona przez japońską wymowę angielska nazwa "Curving Road") - łamigłówka wymyślona przez Naoki Inaba z Japonii. Wygląda jak kwadratowy lub prostokątny diagram z kolami w niektórych komórkach. Należy umieścić czarne komórki według następujących zasad:

• Komórki z kolami nie mogą być czarne.
• Czarne komórki nie mogą stykać się bokami, ale mogą stykać się rogami.
• Wszystkie białe komórki tworzą białe pole, to znaczy stykają się bokami.
• Każda droga od kola do kola musi skręcić co najmniej dwa razy.

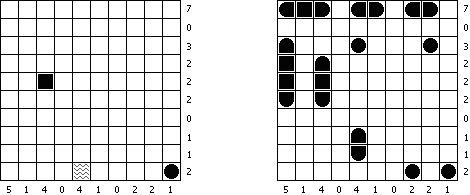
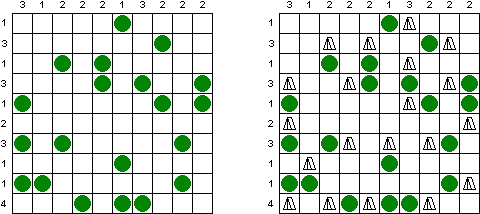
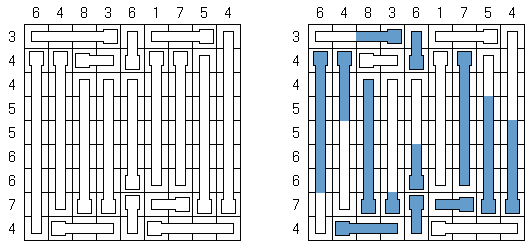
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.

Snake ("Tunnel") is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.

Peintoeria ("Paint Area") is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All cells of a region must have the same color.
• A cell with a number indicates how many black cells are adjacent to it.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the same color.

Irupu ("I-Loop") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.

Sashigane (from Japanese, literally "carpenter's square") is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.

Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

Chocona ("Chocolate") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any number of cells may be blackened.
• The black cells must form rectangles, independently of the region borders.
• The black rectangles must not be orthogonally adjacent.

Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.

LITS ("Nuruomino") is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.

The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.

Nanbaboru ("Number Ball") consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.

Tairupeinto ("Tile Paint", "Crazy Pavement") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.

Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.

Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.

Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.

Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.

Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.

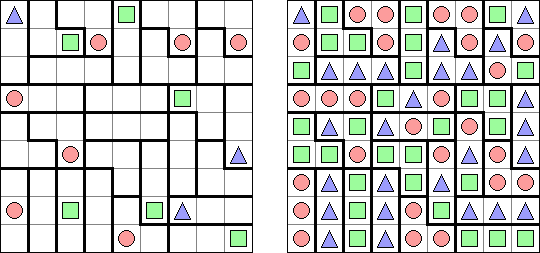
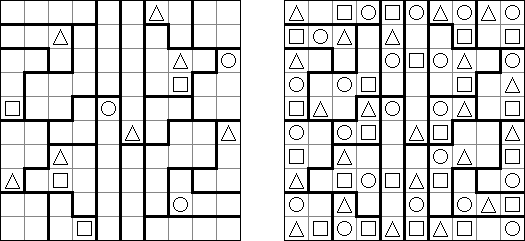
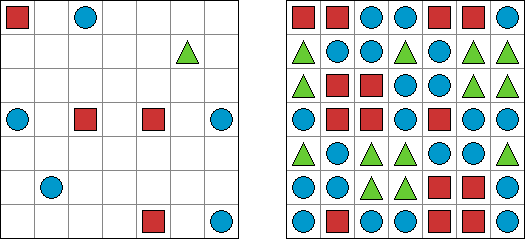
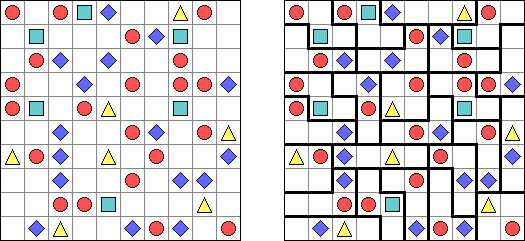
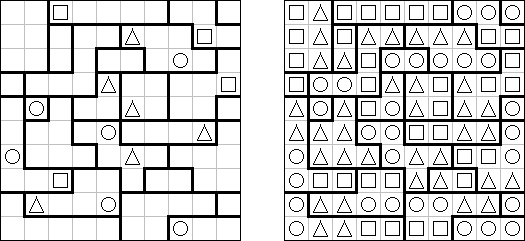
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.

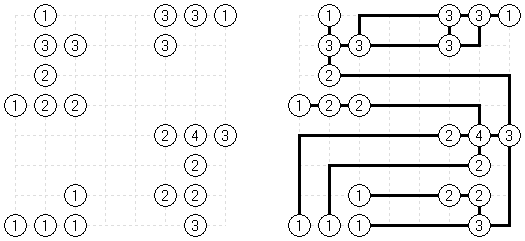
Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.

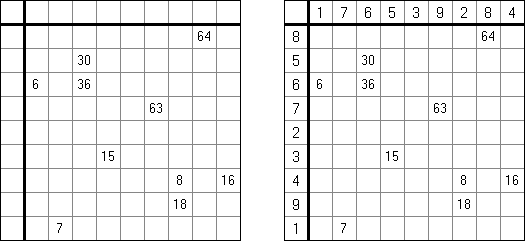
Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.

Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.

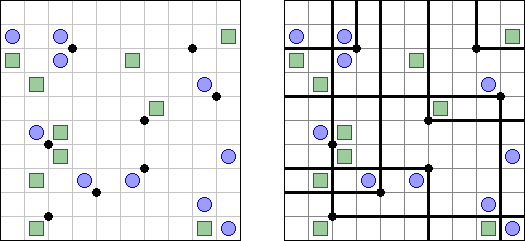
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.

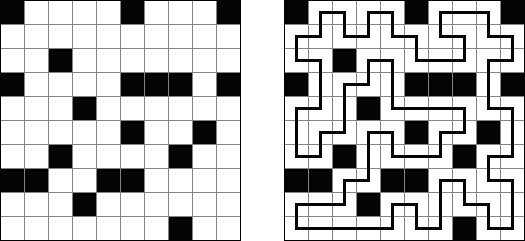
Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.

Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.

Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.

Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.

Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:

• White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle.
• Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.

Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.

Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.

Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.

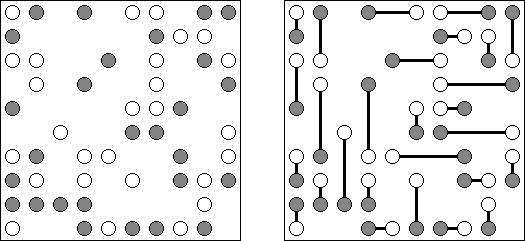
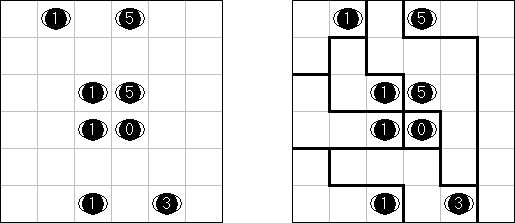
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.

Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.

Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.

Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.

Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:

• Each region contains exactly one arrow.
• Each two arrows are paired, they point to each other. There are no unpaired arrows.
• Two regions with paired arrows must not be horizontally or vertically adjacent.
• Between two paired arrows no other arrow must be placed.

Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.

Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.

Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.

Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• The black cells divide the grid in areas of white cells. Each area contains one cell with a number.
• Each area must have the same number of white cells as the number it contains (including the numbered cell).
• Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide.
• If two stripes are connected diagonally, the length of the stripes must be different.

Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.

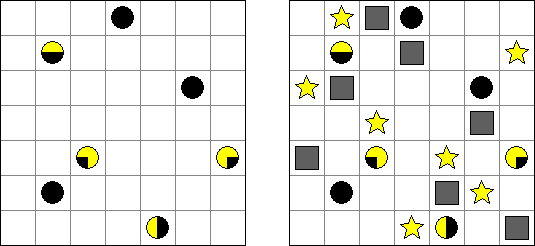
Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.

Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.

Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells).
• Two black cells must not be orthogonally adjacent.
• All of the white cells must be connected.

Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.

Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:

• Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake").
• Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed.
• Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached.
• The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.

Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.

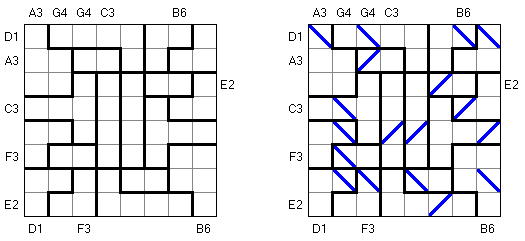
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.

Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.

Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• Two regions with the same amount of black cells must not be orthogonally adjacent.
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.

Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:

• Black cells must not be orthogonally connected.
• A cell with a number may be blacken.
• All the white cells must form an orthogonally continuous area.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.
• Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.

Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:

• A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally.
• A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all.
• A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells.
• Two snakes of the same length must not be orthogonally adjacent.
• A cell with a cross cannot be an end of a snake.

Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:

• Start at any stone.
• When a stone is encountered, it is picked up.
• When a stone is picked up, the direction can be changed.
• It is not allowed to reverse the direction.

Water Fun ("Aquarium") is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.

Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.

Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.

Santoitchi ("San to itchi"; from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:

• All white cells must be divided on regions having the size of exactly three cells.
• Two black cells must not be orthogonally adjacent.
• Each region contains a number.
• A number indicates how many black cells share an edge with that region.

Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.

Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.

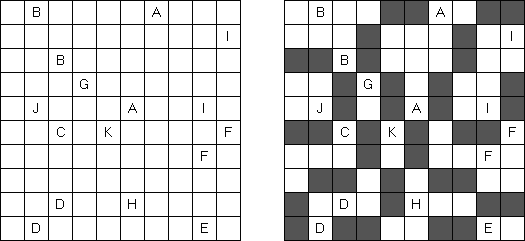
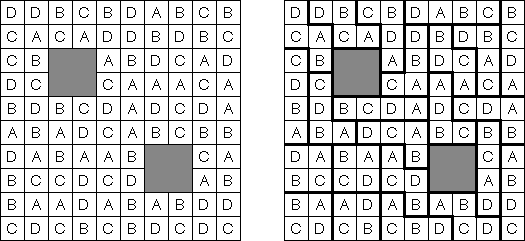
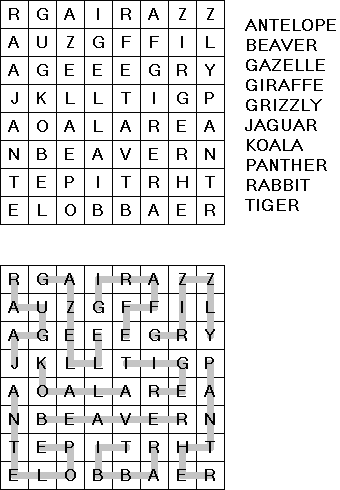
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.

Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.

EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.

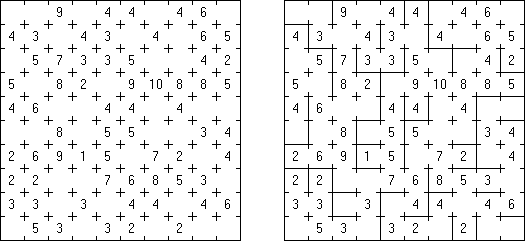
Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.

Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.

Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.

Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:

• All black cells in a region must be connected horizontally or vertically.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• If all stones "fall down", they must cover exactly the bottom half of the grid.

Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.

Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.

Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.

Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:

• Cells with letters, circles or triangles are always white.
• White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide.
• A path from S to G includes all cells with circles and no cells with triangles.
• No 2 x 2 cell area within the grid can have the same color.
• All white cells must form an orthogonally continuous area.
• White cells must not form a loop.

Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:

• All black cells create a single connected group.
• No 2 x 2 cell area within the grid can contain all black cells.
• Numbered cells must not be black.
• Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.

Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.

Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:

• Each region contains one black circle.
• Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.

Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.

Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.

Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.

Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.

Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)

Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.

Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.

Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.

Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules:

• Black cells form an area of square shape.
• No black areas touch each other horizontally or vertically (only diagonally).
• Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size.
• Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.

Gołem Grad ("Golem Grad"; an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:

• The black cells divide the grid into areas of white cells ("islands"), each containing at most one number.
• Two islands may not be connected.
• The island must have the same number of white cells as the number it contains.
• All black cells must form an orthogonally continuous area.
• No 2 x 2 cell area within the grid can have the black color.
• All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid.
• Snakes must not cross each other.

Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:

• No two horizontally, vertically or diagonally adjacent cells contain a digit.
• The numbers across the top and down the left equal the row and column totals for the cells with numbers.
• The numbers across the bottom and down the right are the sums of numbers in the rows and columns.

Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.

Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:

• White cells form a path exactly one cell wide.
• Cells with circles are always white.
• A cell with a circle must have exactly one white cell adjacent to its side.
• A white cell without a circle must have at least two orthogonally adjacent white cells.
• A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself.
• All the white cells must be connected horizontally or vertically.
• No 2 x 2 cell area within the grid can have the same color.

Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:

• The white circle indicates that the sun is closer to the star than the moon.
• The black circle indicates that the moon is closer to the star than the sun.
• The star outside the grid indicates that the circles are at equal distance from the star in that row or column.

Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.

Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.

Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.

Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.

Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)

Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.

Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.

Nuraf ("Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells divide the grid into areas of white cells ("islands").
• Cells with numbers are always white.
• Two islands may not be connected.
• All of the black cells must be connected.
• No 2 x 2 cell area within the grid can have the black color.
• Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.

Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.

Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.

• The same arrows cannot be placed in adjacent cells.
• Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached.
• A cell with a number indicates a total number of arrows that leads to this cell.

Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.

Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.

Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.

Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)

Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.

Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.

Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.

Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.

Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.

Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.

Meandering Numbers (also known as "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)

Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.

Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.

From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.

Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.

Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.

Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.

Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)

Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.

Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).

Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.

Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).

Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.

Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.

Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.

Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.

Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.

Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.

SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.

Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border.
• A cell with a number indicates how many cells in the region must be blackened.
• No two black areas may share an edge.

Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.

Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.

Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.

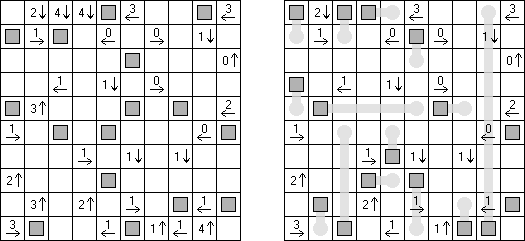
Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.

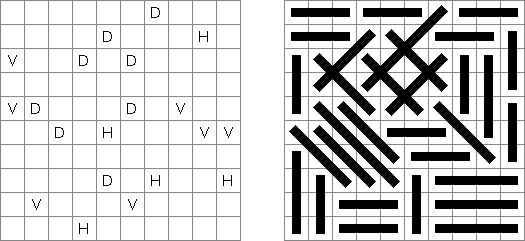
Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.

Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.

Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.

Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:

• The black cells form "islands". No two islands may share an edge; islands may be connected through their corners.
• If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island).
• All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners.
• If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).

Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.

Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected.
• A cell with a number indicates how many cells in the region must be blackened.
• In regions without a number any amount of cells may be blackened (at least one).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All white cells form one orthogonally connected area.
• A line of connected white cells cannot go through two or more region borders.

Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.

Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.

Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:

• The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally).
• A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer.
• Each block contains exactly one number or a question mark.
• All blocks form "chains". A chain is a group of two or more blocks, connected through their corners.
• Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.

Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:

• A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened.
• Blackened cells should not share an edge.
• All the white cells must be connected inside a region (it's possible for a region to have no white cells).
• If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions.
• All the white cells must form an orthogonally continuous area.

Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its N^th entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.

Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.

Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.

Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:

• All black cells in a region must be connected horizontally or vertically (they form a "block").
• A cell with a number indicates how many cells in the region must be blackened.
• In a region without a number any amount of cells may be blackened (all cells may stay white).
• When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
• All blocks of black cells must be connected to each other through their corners.
• No 2 x 2 cell area within the grid can contain all black cells.

Kazoku ("Kazoku shashin"; from Japanese, literally "family photo") is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.

Tontonbeya (from Japanese, literally "gambler") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.

Kontekst ("Context") is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:

• All the white cells must be connected horizontally or vertically.
• A cell with a number can be blacken. Two black cells must not be orthogonally adjacent.
• The number in a white cell indicates the number of orthogonally adjacent black cells.
• The number in a black cell indicates the number of diagonally adjacent black cells.

Word Finder ("Word Search", "Word Seek", "Word Sleuth", "Mystery Word") – kwadratowy lub prostokątny diagram z literami. Należy odnałeżć słówka ukryte w diagramie. Po diagramach można poruszać się poziomo i pionowo; linia może skręcać pod kątem prostym. Każda litera może być wykorzystana tylko w jednym słowie.

Do tworzenia łamigłówki należy zadać listę słów. Można także wskazać słowo kluczowe, które zostanie utworzone z liter, które zostaną po odgadywaniu łamigłówki.

Nine Letters is the variation of Word Finder puzzle. It consists of the grid with letters. The grid is divided on 3 x 3 subgrids. The goal is to find and mark words hidden inside each subgrid.

Pajęczyna ("Spider Web") składa się z kół połączonych ze sobą za pomocą linii. W kolach są umieszczone litery. Należy znaleźć ciągłą sekwencję kół zawierających litery hasła.

Labirynt ("Maze") - struktura składająca się ze skomplikowanych dróg. W łamigłówkach tego rodzaju należy znaleźć drogę pomiędzy dwoma wybranymi punktami. Program pozwala tworzyć labirynty o dowolnym kształcie, nie tylko prostokątne lub kwadratowe.