|
Cross+A  Warianty łamigłówek
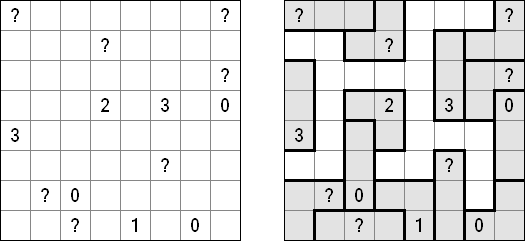
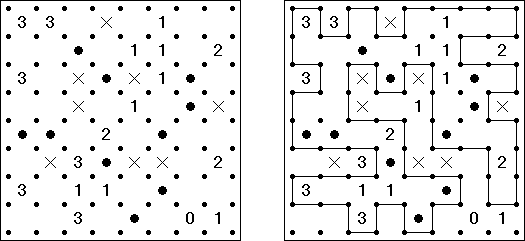
Slitherlink Sheep and Wolves ("Owce i wilki"): oprócz kratek z cyframi od 0 do 3 (cyfry te oznaczają, po ilu bokach tej kratki biegnie pętla) łamigłówka zawiera czarne koła ("owce") i czarne krzyżyki ("wilki"). Należy przeprowadzić pętlę łącząca czarne kropki, tak aby była linią ciągłą, nieprzecinającą się ani nie stykająca się sama ze sobą rogiem. Po rozwiązaniu łamigłówki "owce" muszą znaleźć się wewnątrz zamkniętej pętli, "wilki" - na zewnątrz zamkniętej pętli.
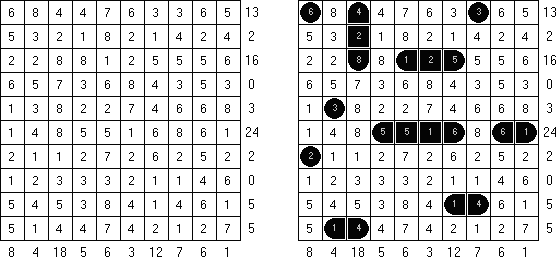
Battleships Digital Battleships zawiera liczby we wszystkich kratkach diagramu. Liczby zewnątrz diagramu – to suma liczb tylko w tych kratkach, które zawierają fragmenty okrętów w odpowiednich wierszach i kolumnach. Okręty, "ukryte" pomiędzy liczbami nie mogą stykać się nawet rogami.
Retrograde Battleships ("Reverse Battleships") contains all segments of the ships in the grid. The aim is to find the correct locations of the ships. No ship may touch another, even diagonally.
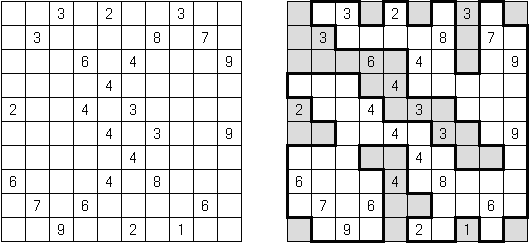
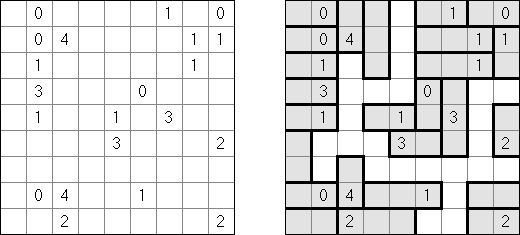
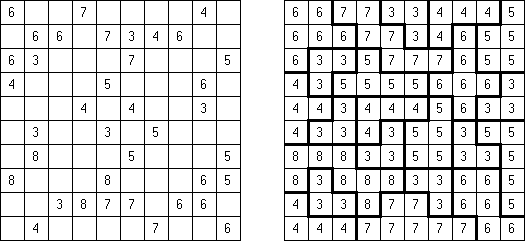
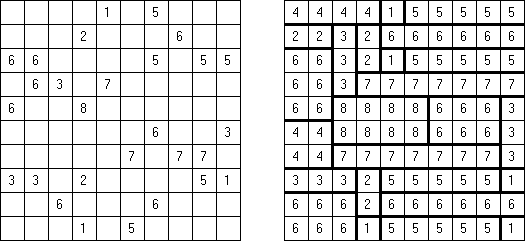
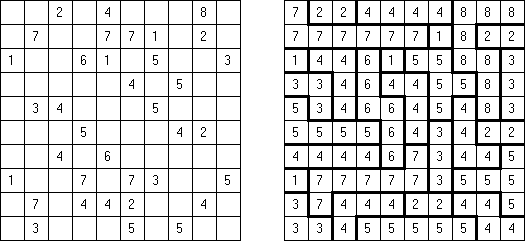
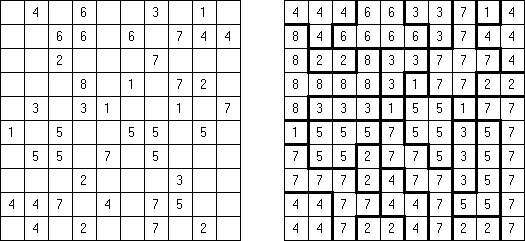
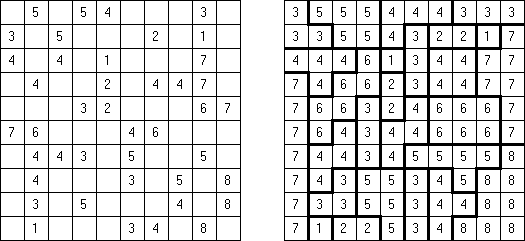
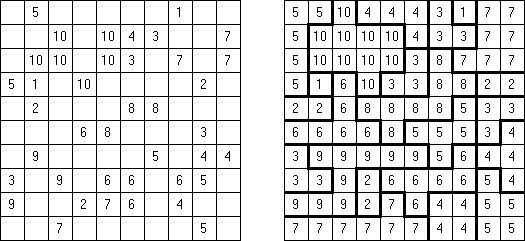
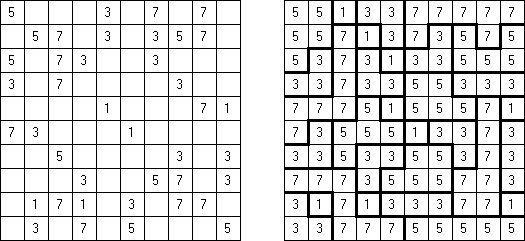
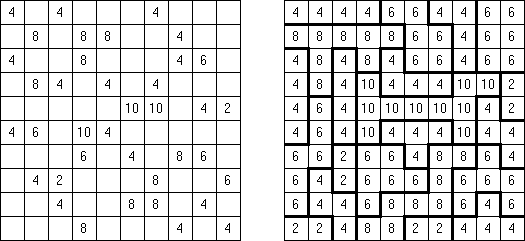
Fillomino No Rectangles Fillomino ma dodatkowy warunek: żaden z bloków nie może być prostokątem lub kwadratem.
Only Rectangles Fillomino: każdy blok musi być prostokątem lub kwadratem.
No 2 x 2 Squares Fillomino: diagram nie może zawierać bloków 2 x 2 z podobnymi liczbami.
Non-Consecutive Fillomino: komórki dwóch stykających się bokami bloków nie mogą różnić się o 1.
Consecutive Fillomino: każdy blok musi stykać się bokami chociaż z jednym blokiem rozmiar którego różni się o 1.
No Row/Column Repeats Fillomino ("Deadomino"): wszystkie podobne liczby w rzędzie albo kolumnie muszą znajdować się w jednym bloku. Na przykład, jeżeli rząd zawiera dwie "5", to znaczy, że obie liczby znajdują się w jednym bloku.
All Odds Fillomino: rozmiary wszystkich bloków są nieparzyste.
All Evens Fillomino: rozmiary wszystkich bloków są parzyste.
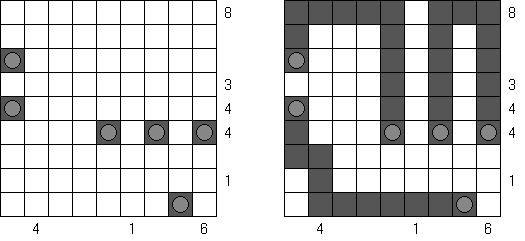
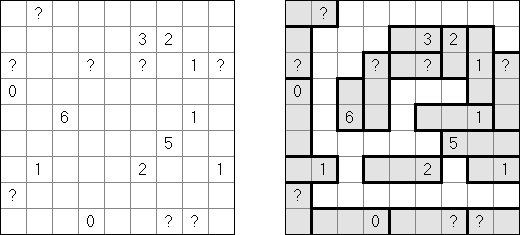
Nurikabe Line Nurikabe: a grid cannot contain five consecutive black cells in a row or column (2 x 2 cell area can be all black).
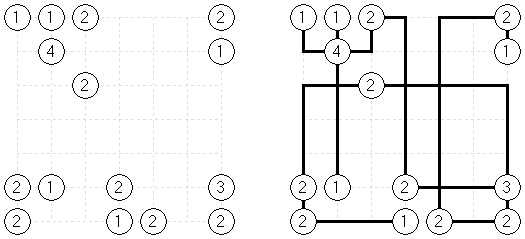
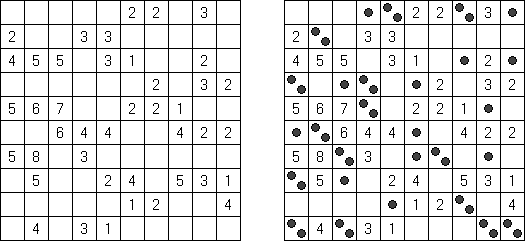
Pairs Nurikabe różni się od zwykłej łamigłówki tym, że każda "wyspa" zawiera dwie liczby, suma których jest równa polu powierzchni wyspy.
Skyscrapers Sum Skyscrapers różni sie od zwykłej łamigłówki tym, że liczby zewnątrz diagramu oznaczają nie ilość widocznych wieżowców, a sumę pięter wieżowców.
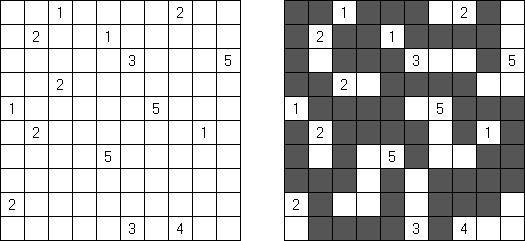
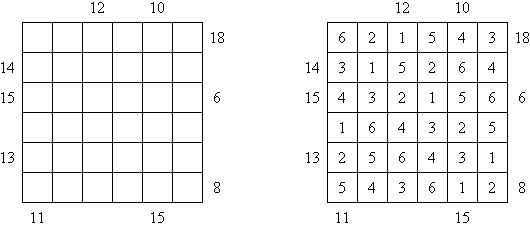
Tapa Istnieje wiele odmian łamigłówki Tapa. Program Cross+A może rozwiązywać niektóre. W odmianie Tapa [Line] jest dodatkowy warunek: nie może być poprowadzona linia z czterech kolejnych czarnych komórek.
No Squares Tapa: nie może zawierać żadnego kwadratu 2 x 2 z białych komórek.
Equal Tapa: ilość białych komórek (z wyjątkiem tych, które zawierają liczby) musi być równa ilości czarnych komórek.
B&W Tapa:
Tapa Islands:
Pata:
Tapa Balance: ilość czarnych pól w lewej części diagramu jest równa ilości czarnych pól w prawej części diagramu. Białe pola i pola z liczbami nie przyjmują się do uwagi.
Tapa Row: suma cyfr w rzędzie jest równa ilości czarnych pól w tym rzędzie.
Tapa 1-n: wszystkie rzędy i kolumny muszą zawierać różną ilość czarnych pól.
Dissected Tapa: czarne i białe komórki tworzą dwie przystające figury. Dwie figury uważa się za przystające jeśli między nimi istnieje identyczność kształtu i wielkości.
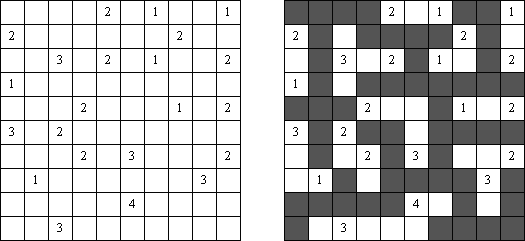
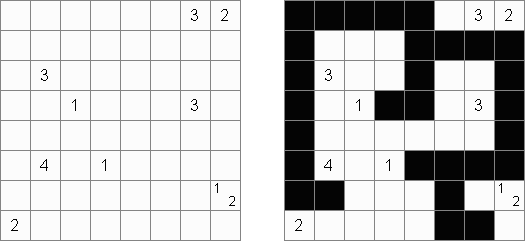
Tapa [Diagonal Neighbors]: każda czarna komórka musi mieć chociaż jedną sąsiędnią czarną komórke stykającą się z nią rogami.
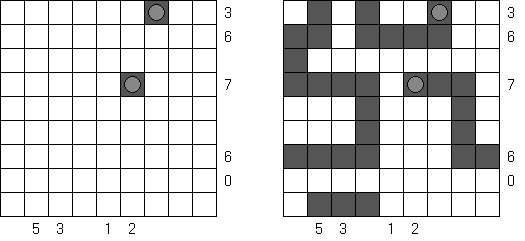
Corral Inside/Outside Corral is a variation of Corral puzzle. The numbers can be inside the loop and outside the loop. In both cases the number indicates how many cells can be seen horizontally and vertically from that cell, including the cell itself.
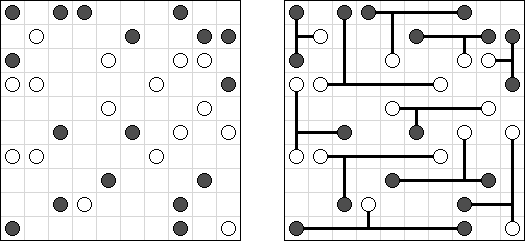
Arukone Arukone3:
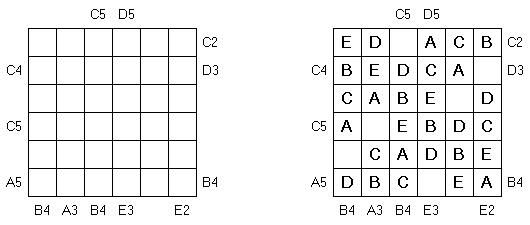
Easy as ABC Not as Easy as ABC is a variation of Easy as ABC puzzle. The goal is to fill in the first letters of the alphabet on every row and every column exactly once. One cell in every row and every column remains empty. Letters and numbers on the outside indicate at what position you come across this letter when looking from that side (e.g. C2 means the C is the second letter encountered when looking from that side).
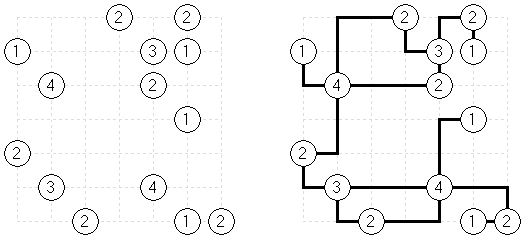
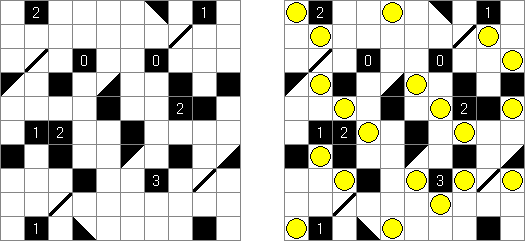
Ichimaga Crossing Ichimaga: the lines may cross other lines; the lines cannot change direction at the point of intersection.
Magnetic Ichimaga ("Jishaku-Ichimaga"): the circles with the same digits cannot be connected.
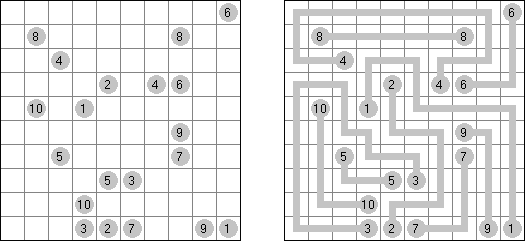
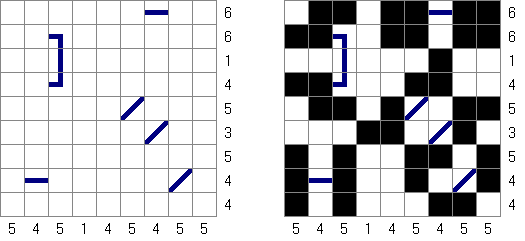
Snake Multiple Snakes: a grid contains multiple snakes. Head and tail of all snakes are given. Different snakes do not touch each other, even diagonally.
Toroidal Snake: a grid wraps around itself. A snake can go from one edge to another.
Minesweeper Double Minesweeper: place mines into each empty cell in the grid, at most two mines per cell.
Mirukuti Milk Tease is a variation of Mirukuti ("Milk-T") puzzle. T-shaped line may connect:
Two circles of the same color must be connected by the straight-line segment of the T-shaped line.
Akari Mirror Akari ("!irakAkari!"): a square or rectangular grid contains diagonal walls (black triangles) with mirrors.
Tren Tren+:
Ghost Tren:
Mubunanba Mubunanba+:
Yajilin Regional Yajilin (also known as "Yajilin (Regions)") is a square or rectangular grid divided into regions. The aim is to blacken some cells and to draw a single non-intersecting loop through all the white cells. A number in a region indicates the number of black cells in that region. A region without a number can contain any amount of black cells. No two black cells can share a border. The loop may visit numbered cells; numbered cells can be blackened.
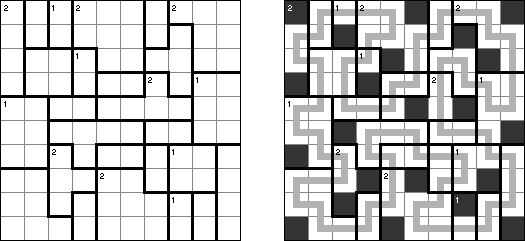
LITS Double LITS has one difference from the classic variant of the puzzle: each region must contain two tetrominoes. These two tetrominoes within a region cannot touch each other horizontally or vertically (only diagonally); they can be the same or different shapes.
Kapama Sunglasses is a logic puzzle. A rectangular or square grid contains lines ("bridges") in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes ("lenses") are symmetrical with respect to a bridge. Two lenses may not share an edge. Cells with bridges can not be blacken. Numbers outside the grid show the number of black cells in a corresponding row or column.
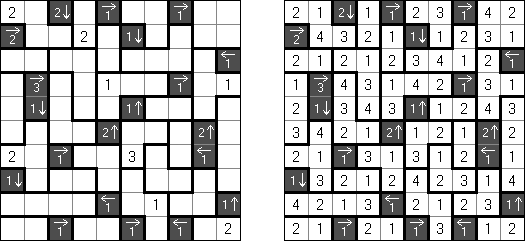
Makaro Masakuchi is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. The grid may contain black cells with arrows and numbers: the arrow points at the greatest number among the four cells around (up, under, left, right) the black cell. The number in the black cell shows the difference between the greatest number and the second highest number in all orthogonally adjacent cells around the black cell.
|
![Tapa [Line]](../data/tapa1.gif)
![Tapa [Diagonal Neighbors]](../data/tapa11.gif)
