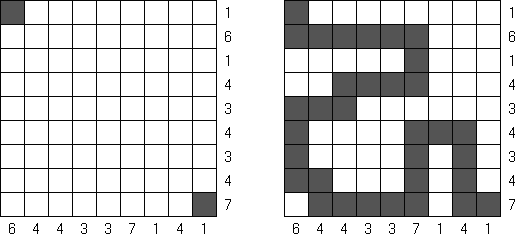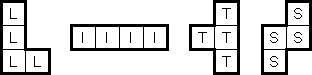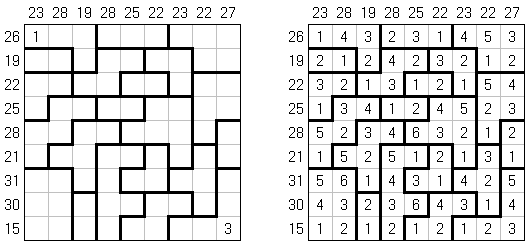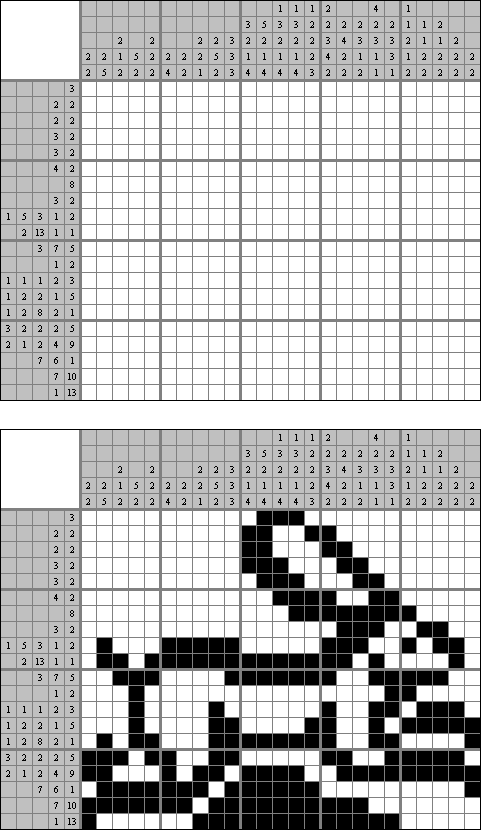
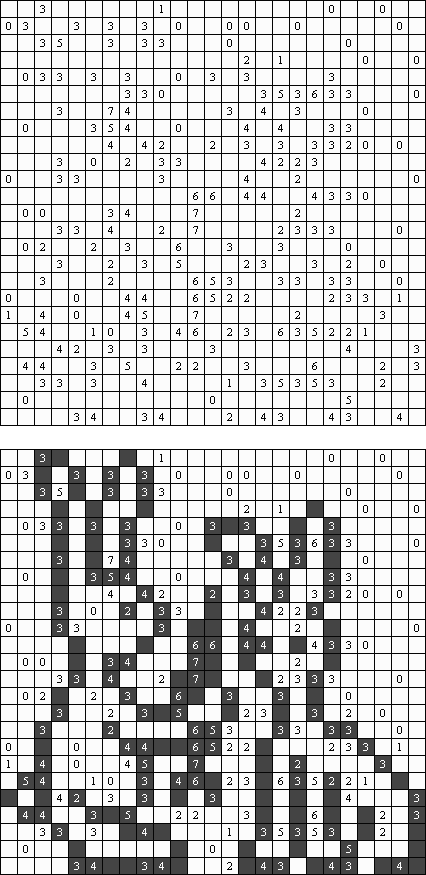
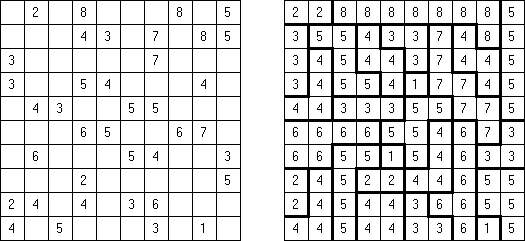
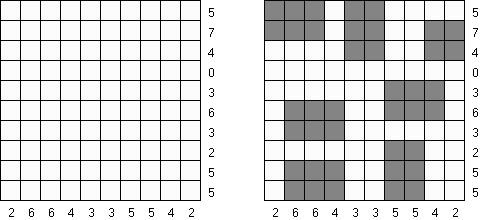
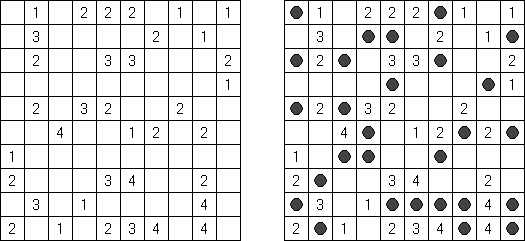
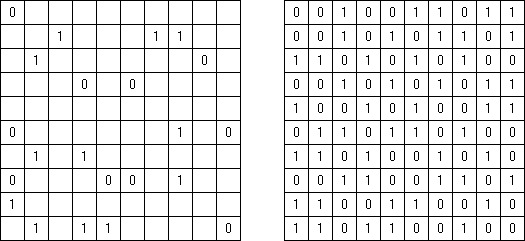
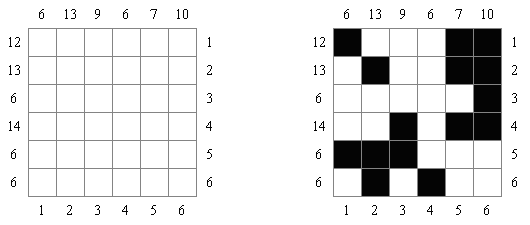
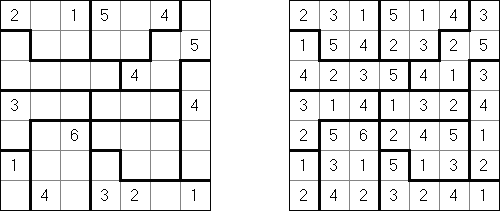
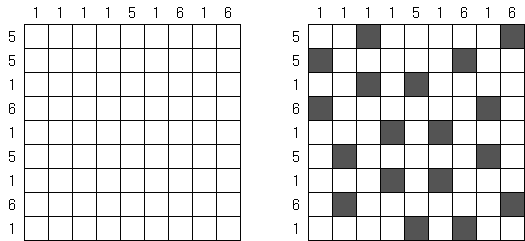
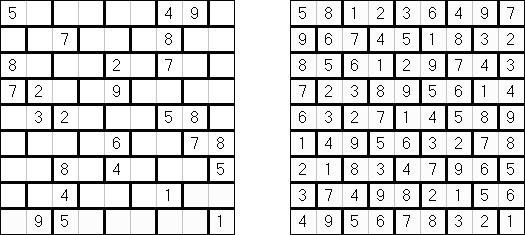
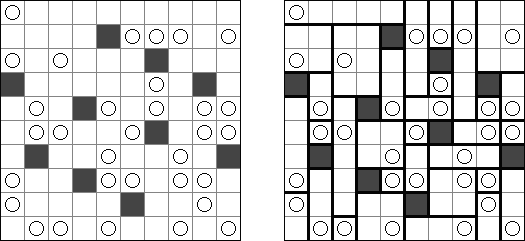
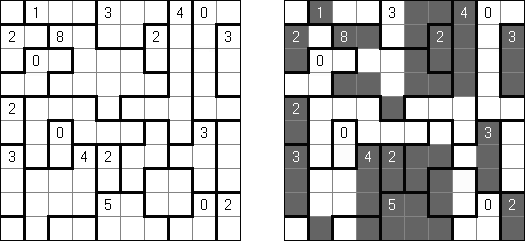
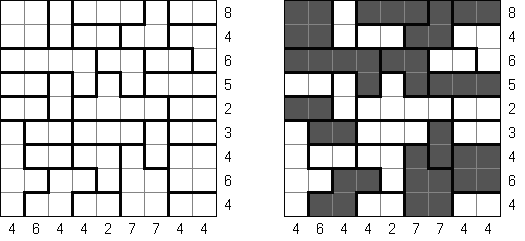
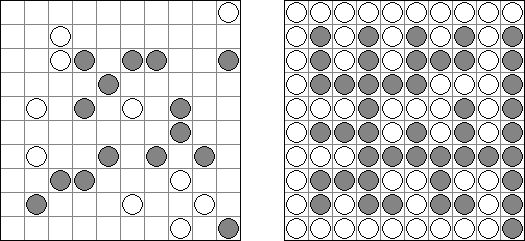
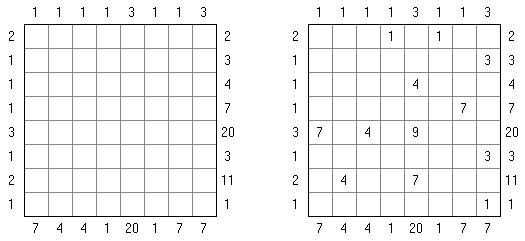
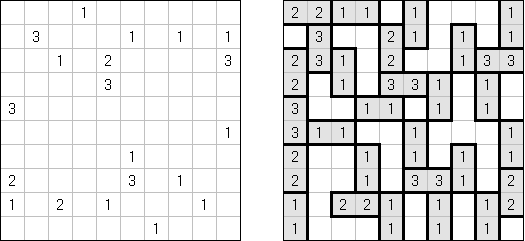
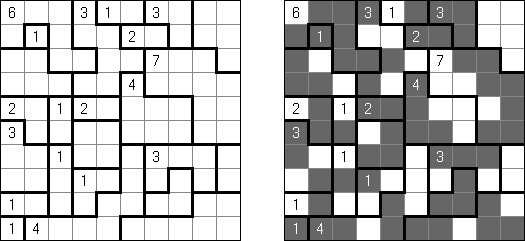
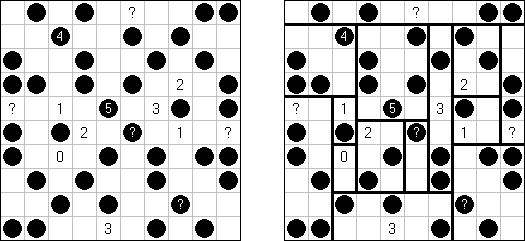
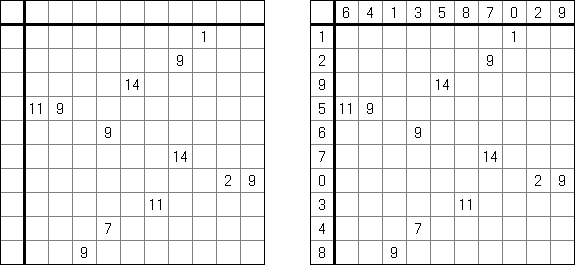
Cross+A Pasatiempos

Cross+A sirve para solucionar y crear rompecabezas lógicos de muchos varios tipos. El rompecabezas creado se puede guardar como un fichero gráfico (los formatos soportados son: BMP, EPS, GIF, JPEG, PNG, PDF, SVG, TIFF, metaarchivos de Windows y ficheros de CorelDRAW). Además, se puede usar el modo de paquetes para crear los rompecabezas.

Nonograma ("Hanjie", "Paint by Numbers", "Griddler") presenta una malla cuadrada o rectangular en que se puede reconstruir unas imágenes según los números dados. Los números situados a la izquierda de las filas y encima de las columnas indican la cantidad de grupos de celdas negras en la línea correspondiente y la cantidad de celdas negras consecutivas en cada grupo. Por lo menos una celda vacía separa los grupos.

El programa Cross+A sabe solucionar tanto nonogramas en blanco y negro, como de color. El propio usuario fija las dimensiones de la imagen en vertical y en horizontal y depués, usando la coma, da los números que describen los grupos de celdas negras o de color en filas y columnas. Se puede aguardar el texto del partido en un fichero para no darlo cada vez de nuevo; así mismo se puede aguardar la imagen de solución como un fichero gráfico o HTML.

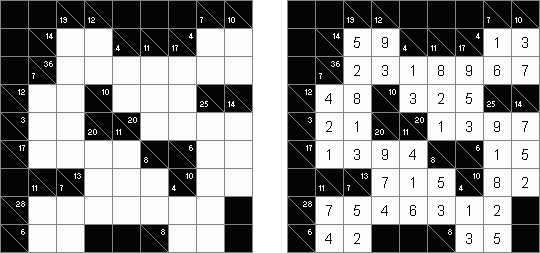
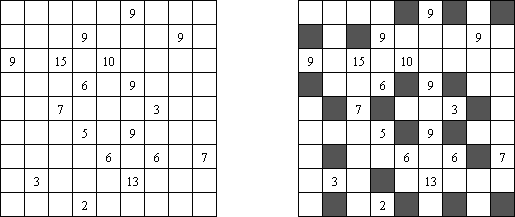
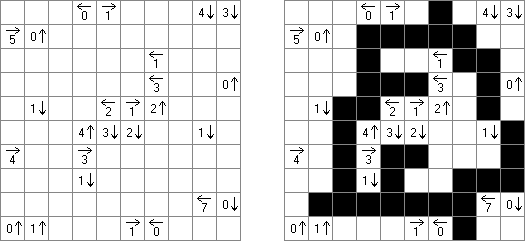
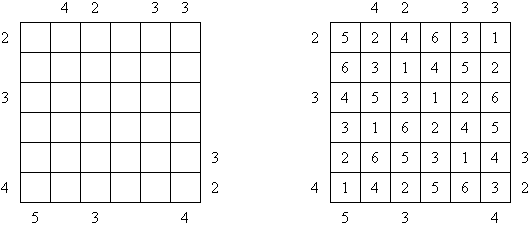
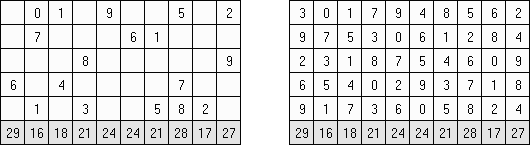
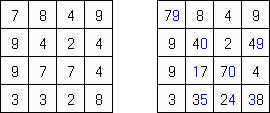
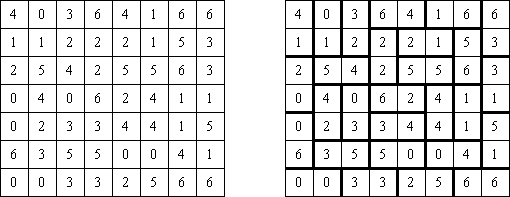
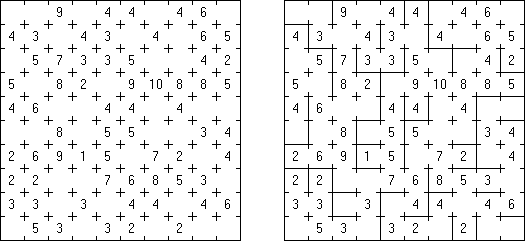
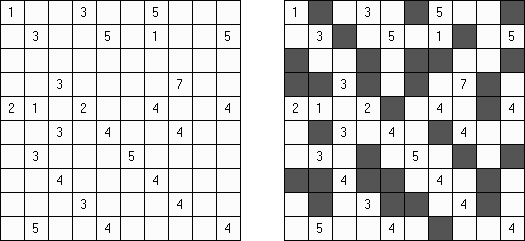
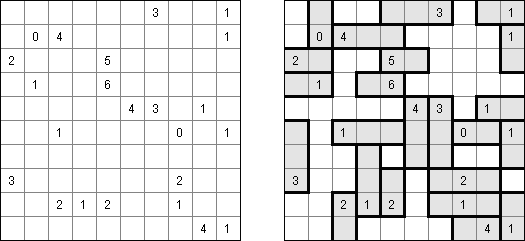
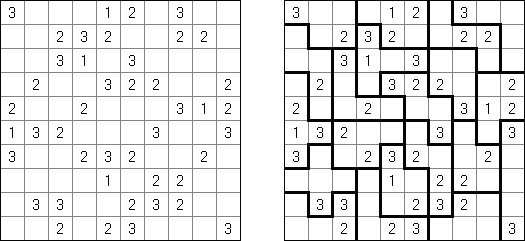
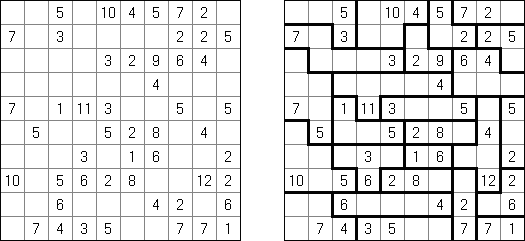
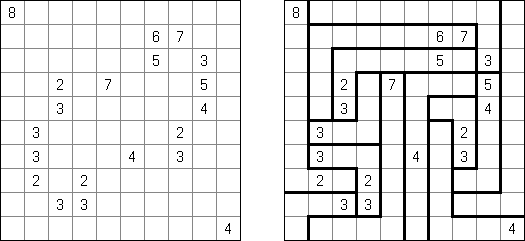
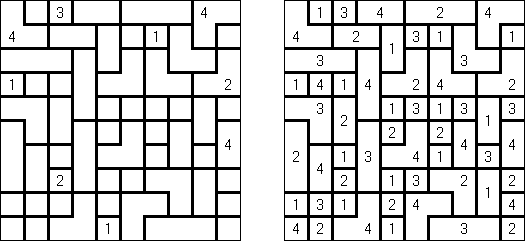
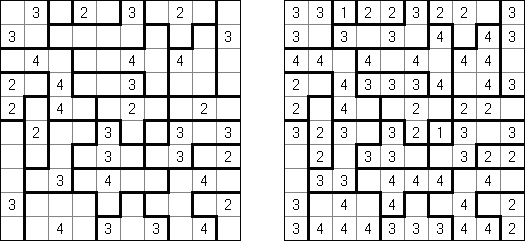
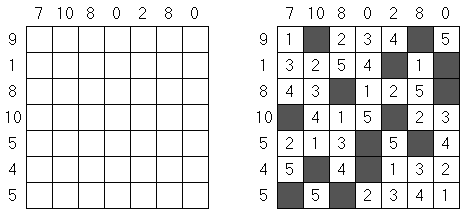
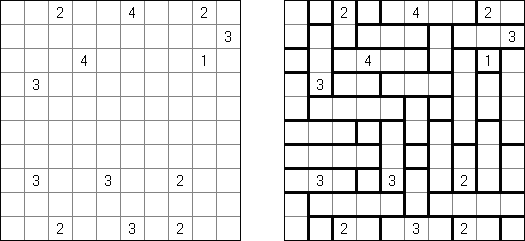
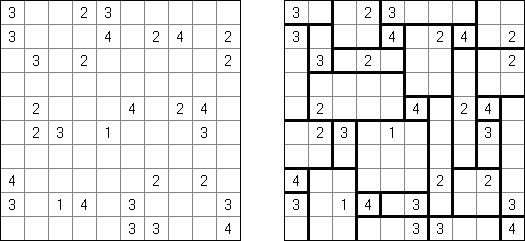
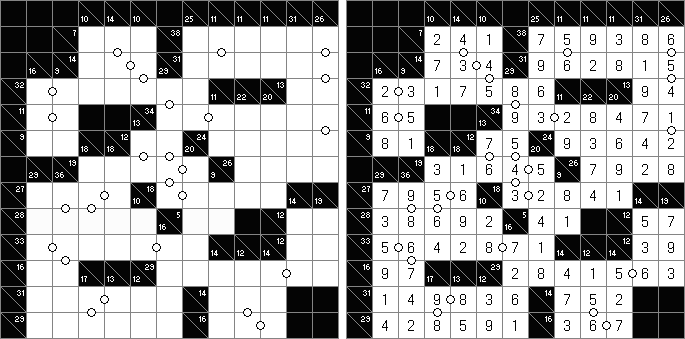
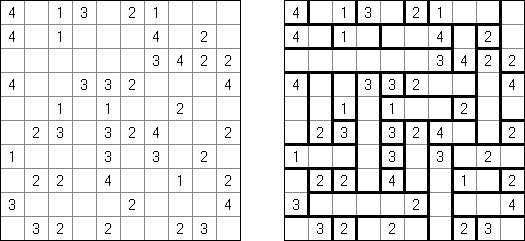
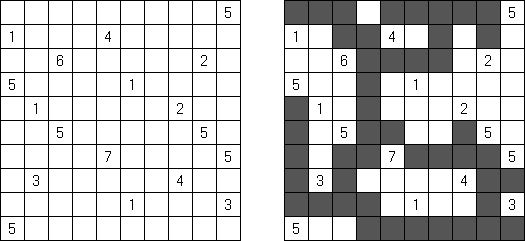
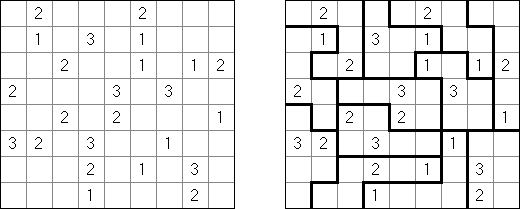
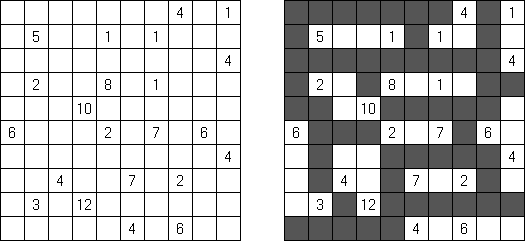
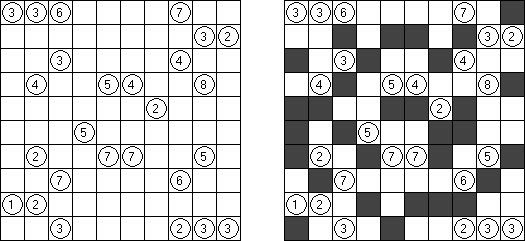
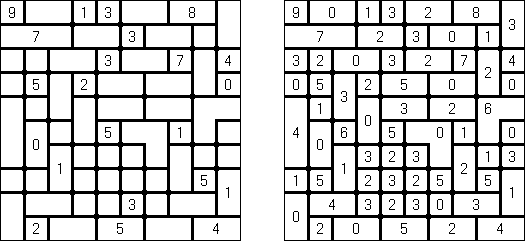
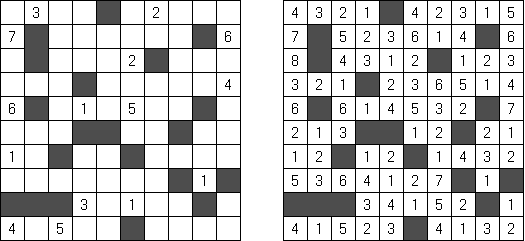
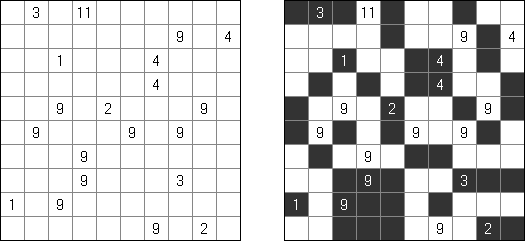
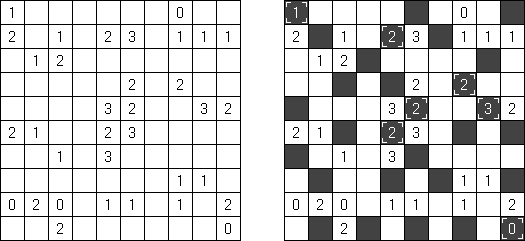
Kakuro ("Cross Sums"), un pasatiempo numérico, es un variante matemático de crucigrama. El objetivo es introducir los números de 1 a 9 en todas las celdas sino negras que son inactivas. En las celdas con los números dados la cifra alta derecha significa la suma de los números en la columna y la cifra baja izquierda significa la suma de los números de la columna que está debajo de la celda. Por ejemplo, se puede presentar el número 6 como suma de 1 y 5 ó de 2 y 4. No se puede usar los mismos números (3 y 3).

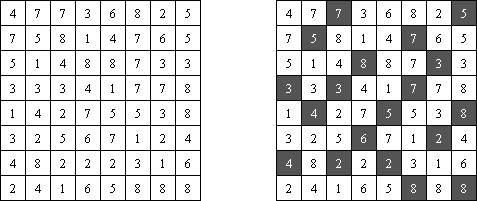
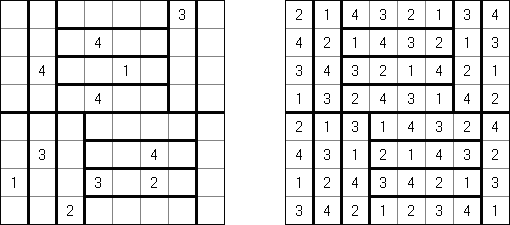
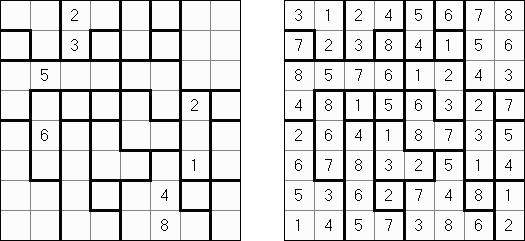
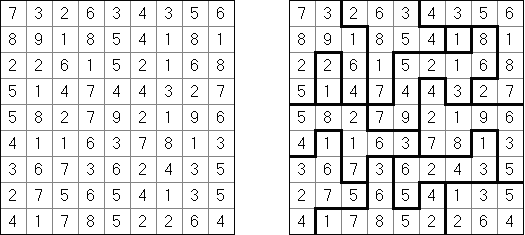
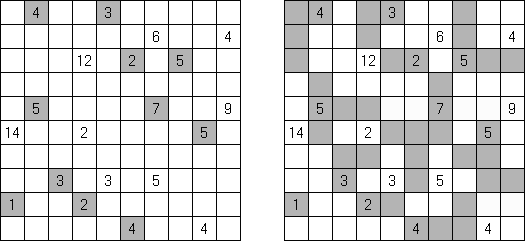
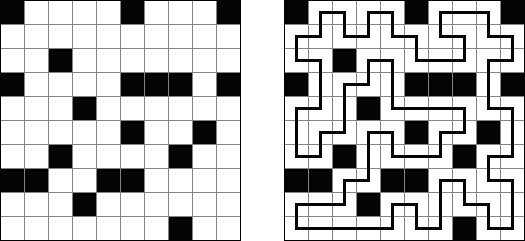
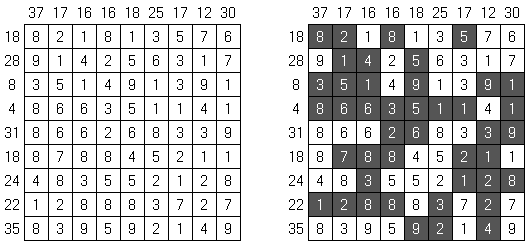
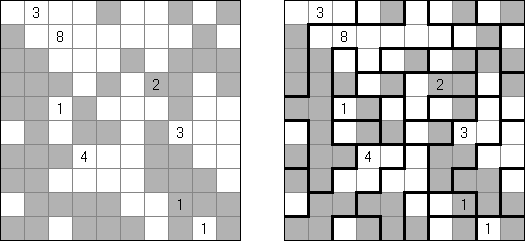
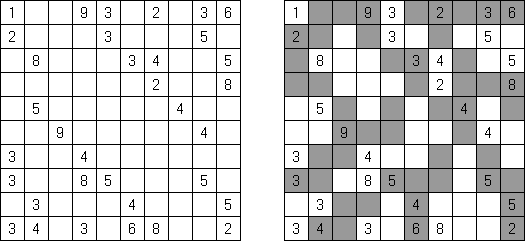
Hitori es un pasatiempo lógico. Hay que tachar los números repetidos para que no se aparezca el número en la misma columna o fila más de una vez. Pueden tocarse las esquinas y no lados de las celdas tachadas. Las celdas no tachadas deben formar un espacio "blanco" conexo sin aislarse una de otra.

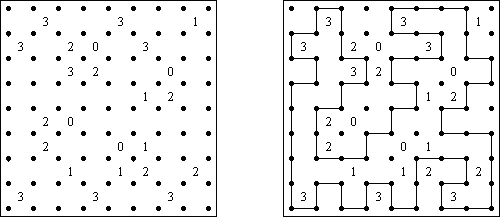
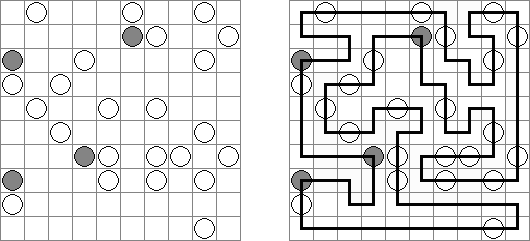
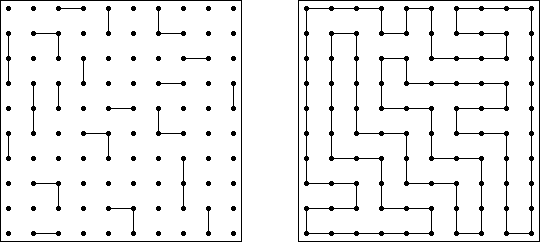
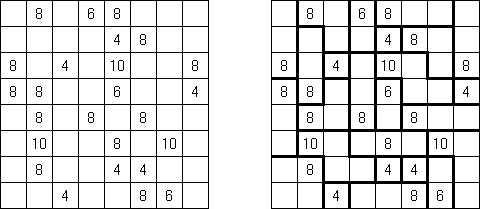
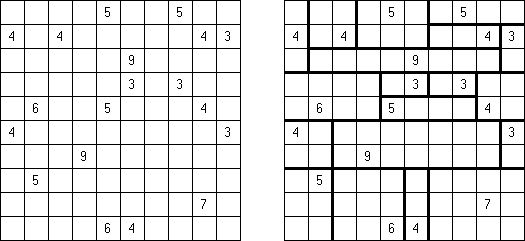
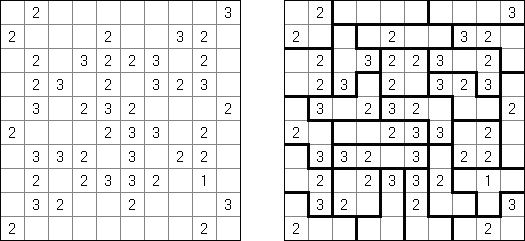
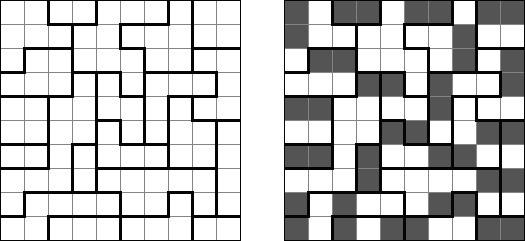
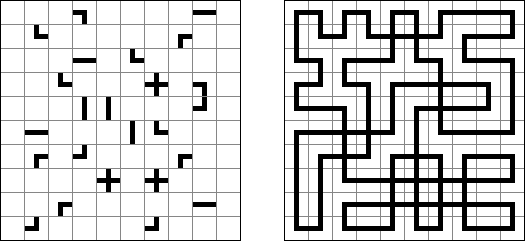
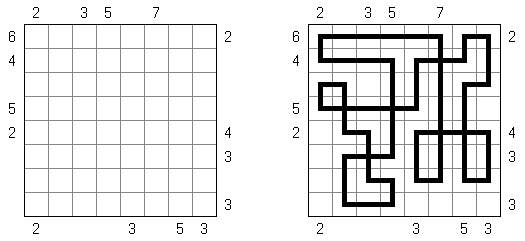
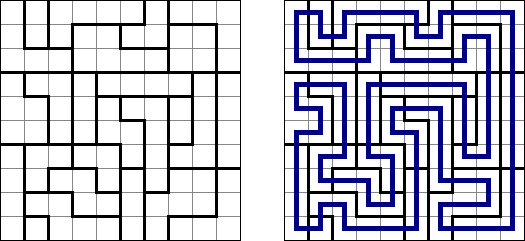
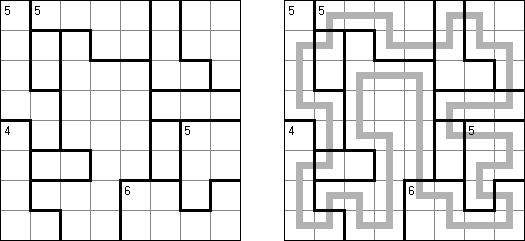
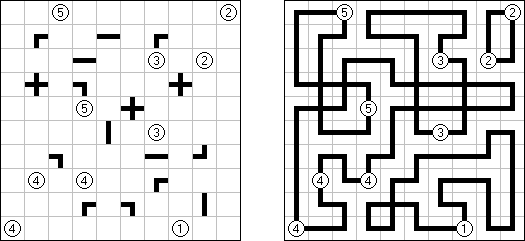
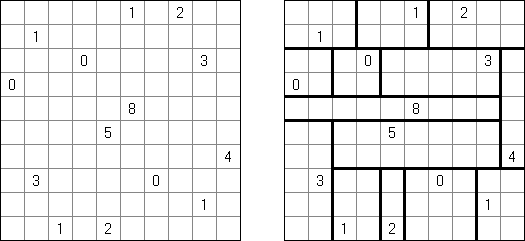
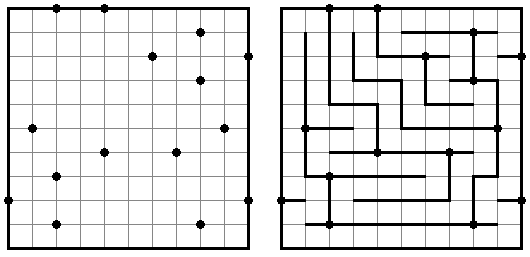
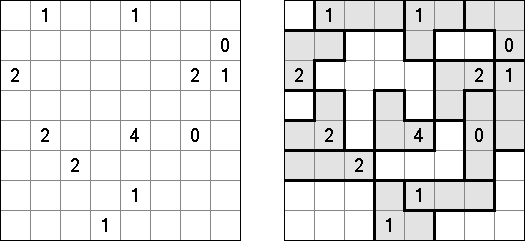
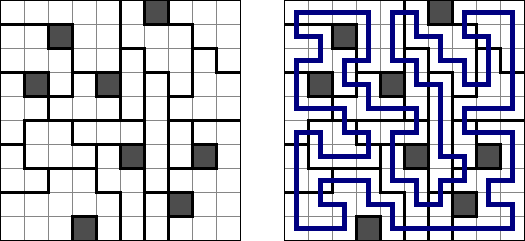
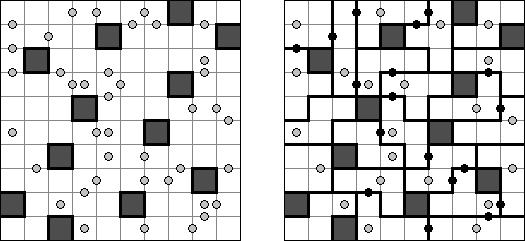
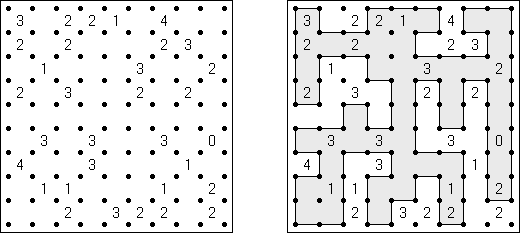
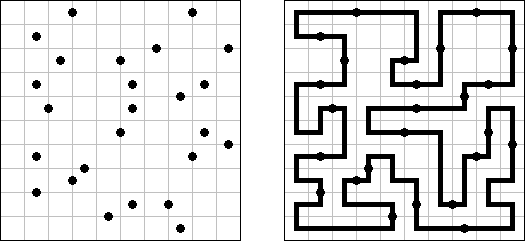
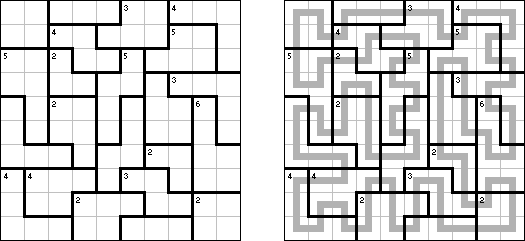
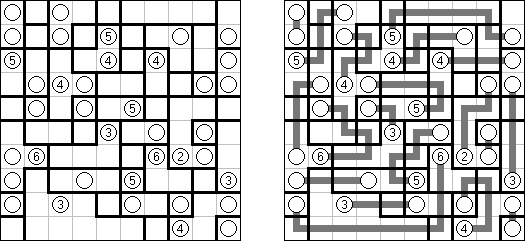
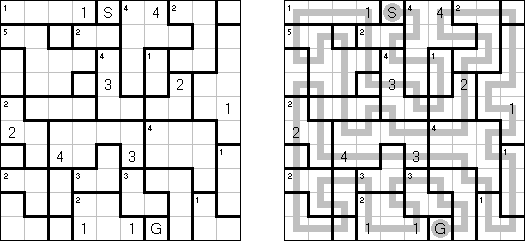
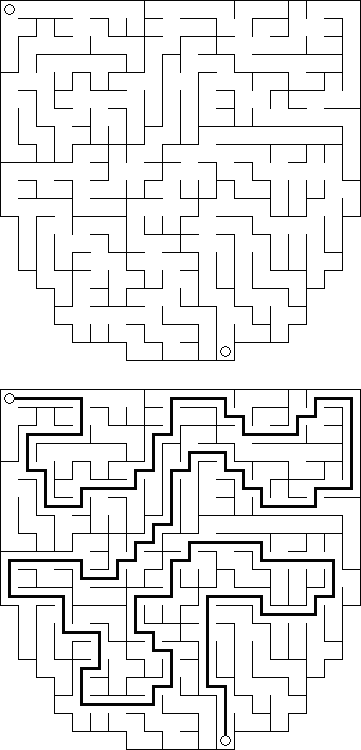
Slitherlink ("Fences", "Loop the Loop", "Puzzle Loop", "Loopy") es un pasatiempo lógico muy parecido al laberinto. El objetivo es con la ayuda de líneas rectas, verticales y horizontales, unir los puntos de manera que se forme un ciclo sin cortarse a si mismo. Cada número indica cuantas líneas deben estar en su perímetro. Si no hay número el la celda, se puede situar cualquier número de líneas en torno de esta.

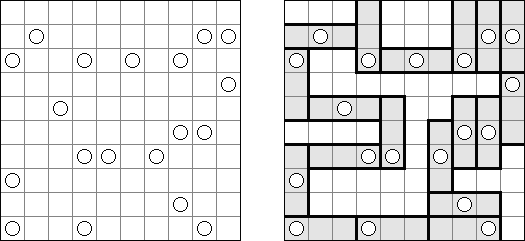
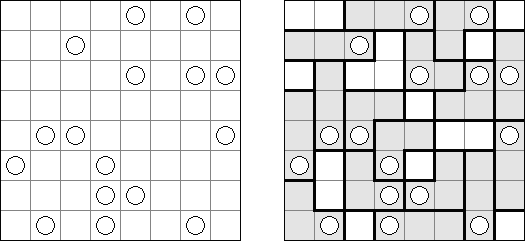
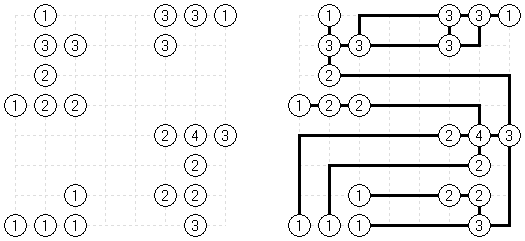
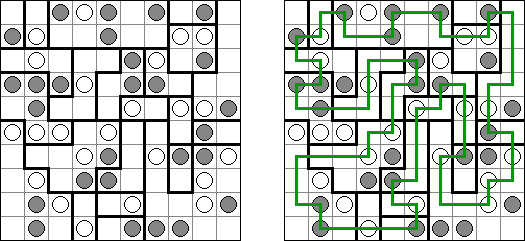
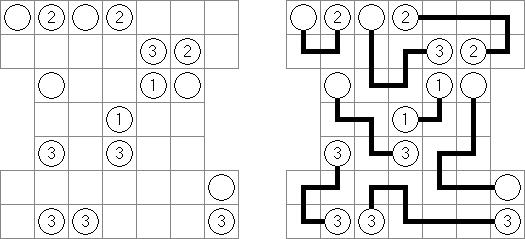
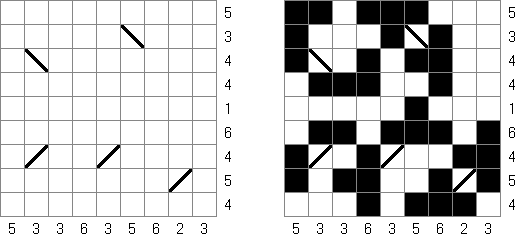
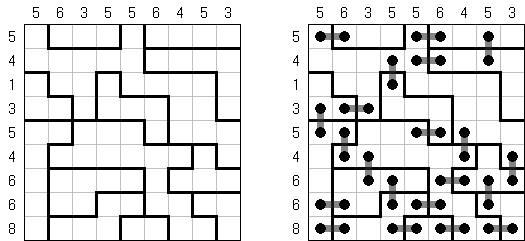
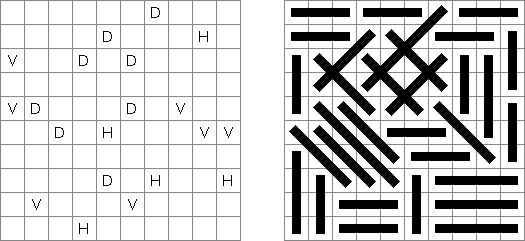
Link-a-Pix ("Paint by Pairs") es un pasatiempo numérico. Cada número en la cuadrícula, excepción hecha para 1, tiene su pareja. Hay que encontrar las parejas y unirlas con las líneas. La cantidad de celdas en la línea debe ser igual a los dos números en sus fines. Las líneas pueden qebrarse, ser horizontales o verticales, pero no diagonales. Las líneas no pueden cruzarse y pasar por mismas celdas.

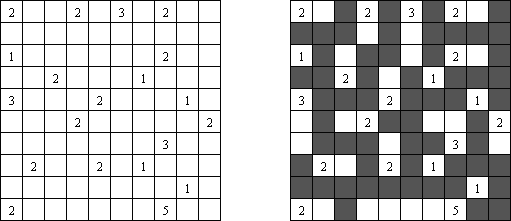
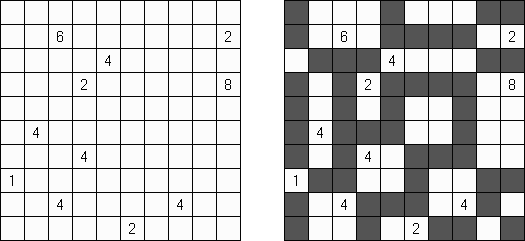
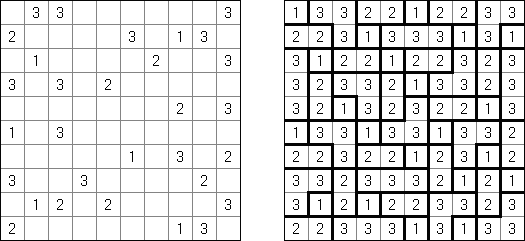
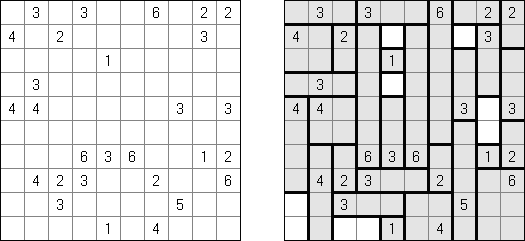
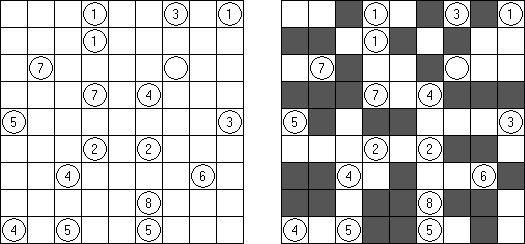
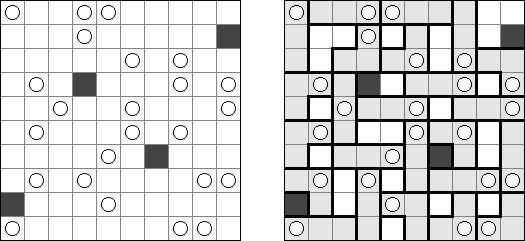
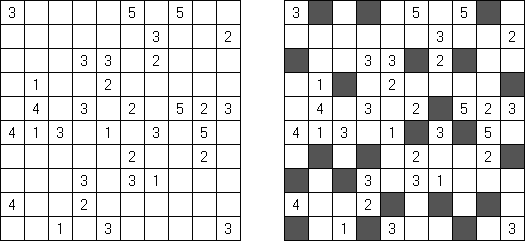
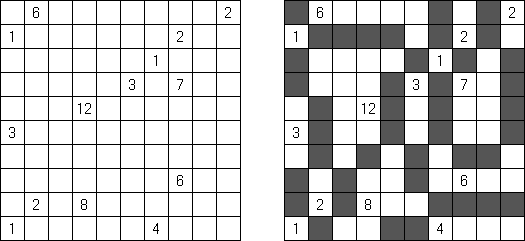
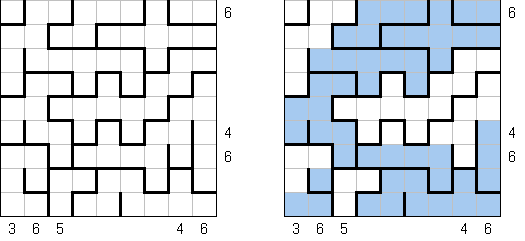
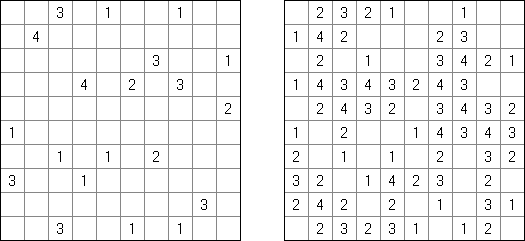
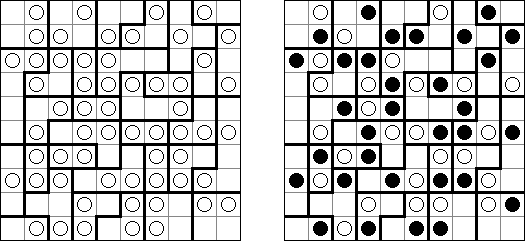
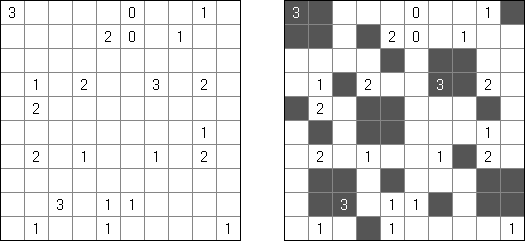
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") es un pasatiempo lógico con una imagen cifrada con la ayuda de números. Cada número indica cuantas celdas adyacentes, incluyendo esta misma, hay que rellenar de color. Por ejemplo, si está en la celda el número 0, no hay que rellenar ni esta, ni vecinas.

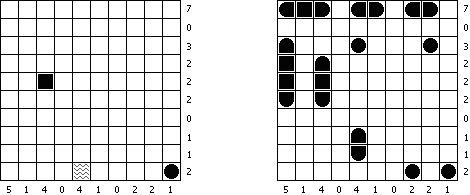
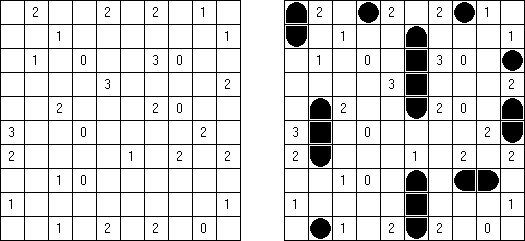
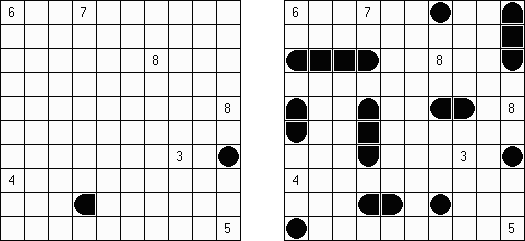
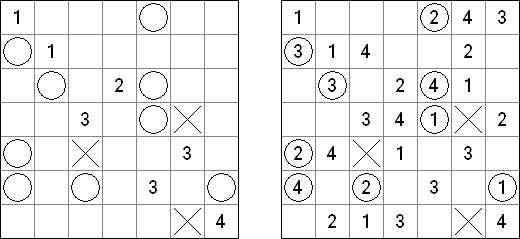
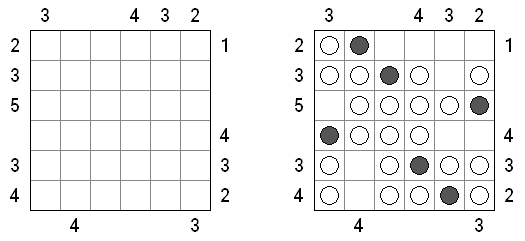
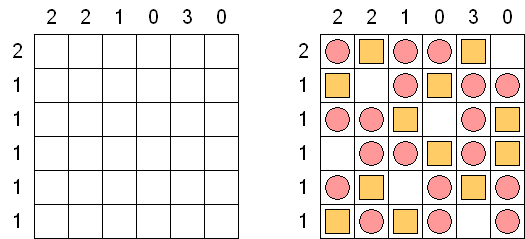
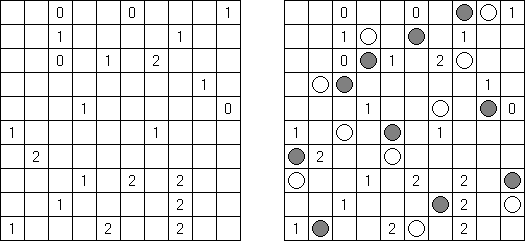
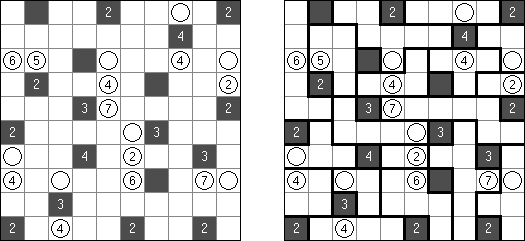
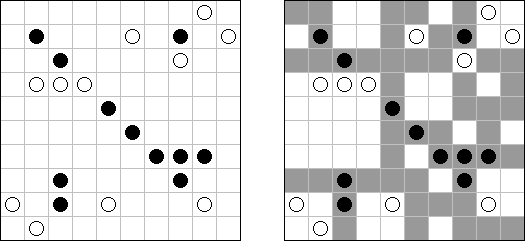
Batalla naval ("Battleships", "Solitaire Battleships", "Battleship Solitaire") es un pasatiempo muy parecido al juego popular "Hundir la flota". El objetivo es situar los barcos de manera que no se toquen sus esquinas. Los números al lado y debajo muestran cuantos fragmentos de los barcos contiene la fila o la columna.

De ordinario la cuadrícula es de 10 x 10 celdas. Toda flota tiene 10 barcos: un barco de 4 celdas, dos de 3 celdas, tres de 2 celdas y cuatro de 1 celda. En algunos partidos algunos fragmentos de los barcos pueden ser abiertos ya.

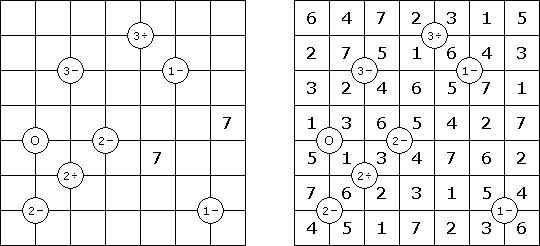
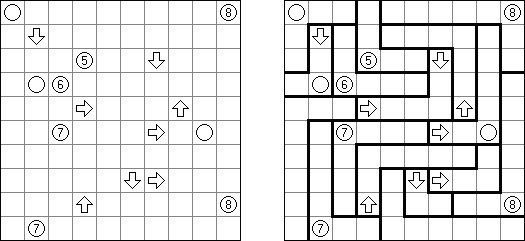
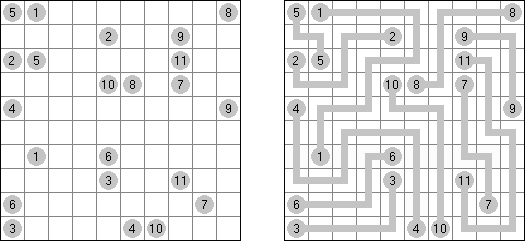
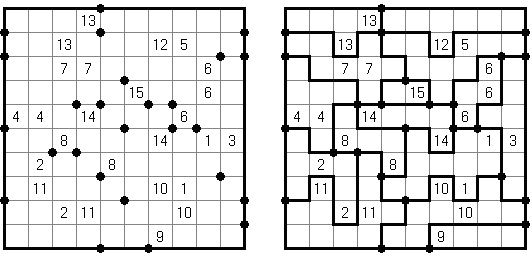
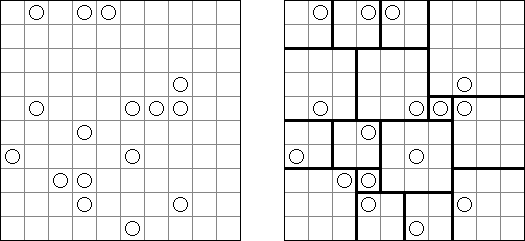
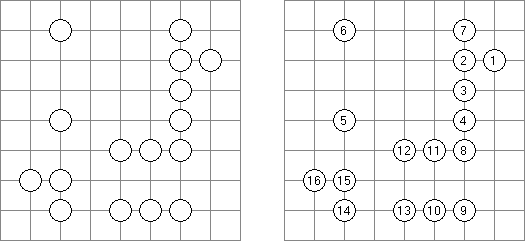
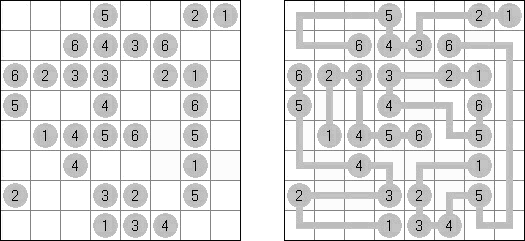
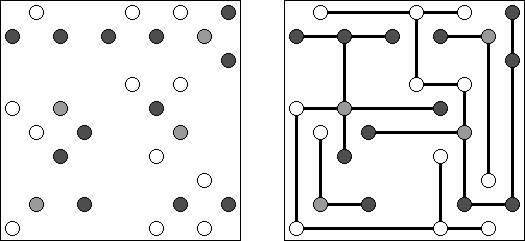
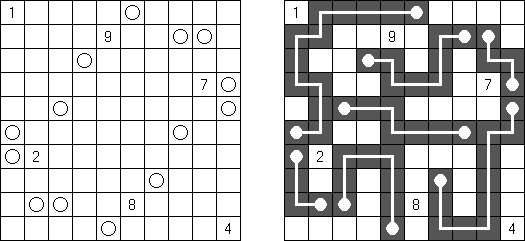
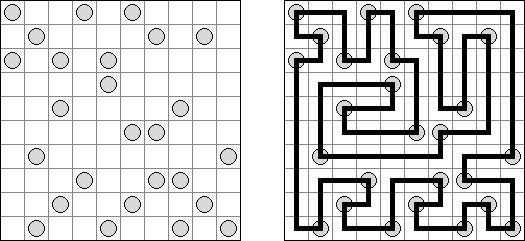
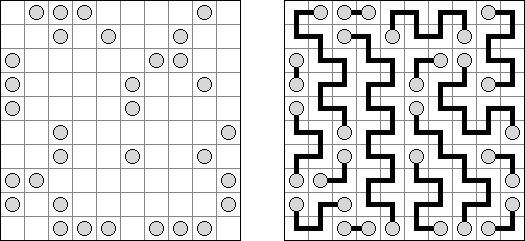
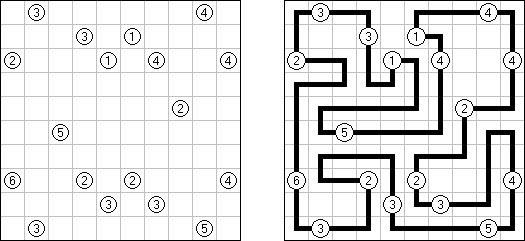
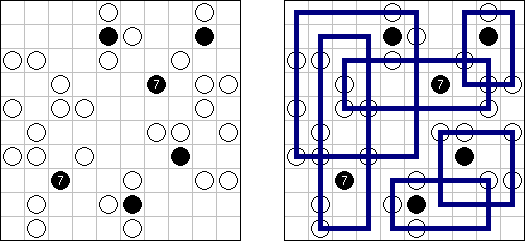
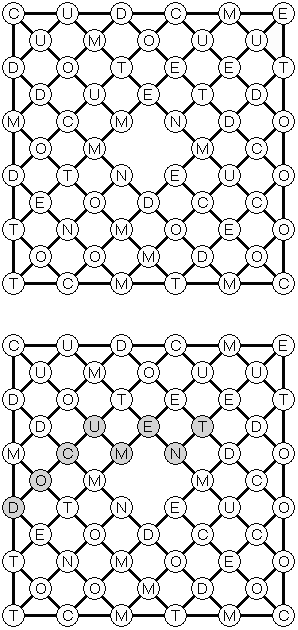
Hashiwokakero ("Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai") es un pasatiempo en que uno tiene que unir los círculos ("islas") por líneas rectas ("puentes"). El número dentro de la "isla" indica en cuantos puentes participa la isla. No se permiten islas aisladas: de cada isla uno debe llegar a cualquiera otra isla.

No pueden existir mas de 2 puentes entre 2 islas. Las líneas pueden ser verticales, horizontales y no diagonales. No pueden las líneas cruzarse, quebrarse o atravesar las islas.

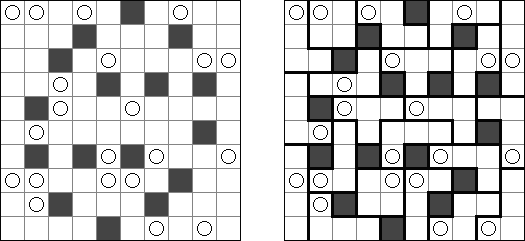
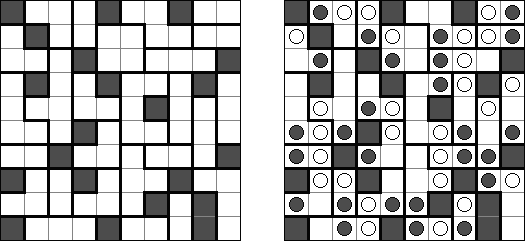
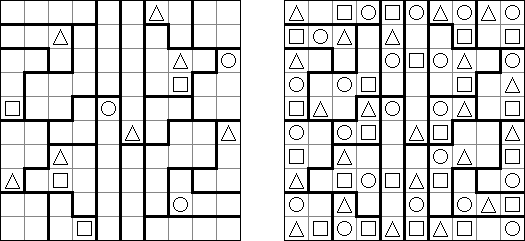
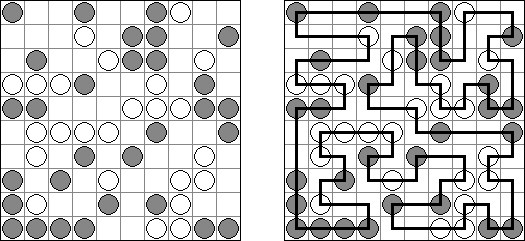
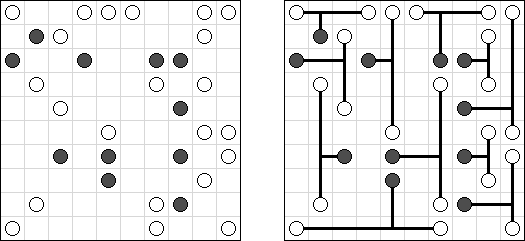
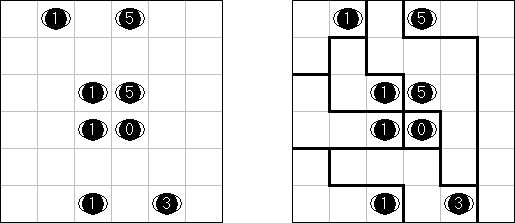
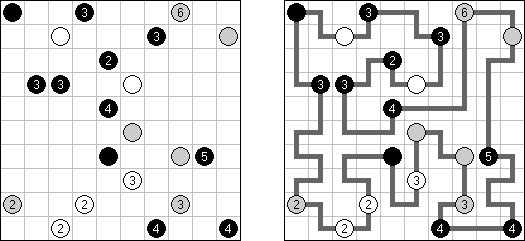
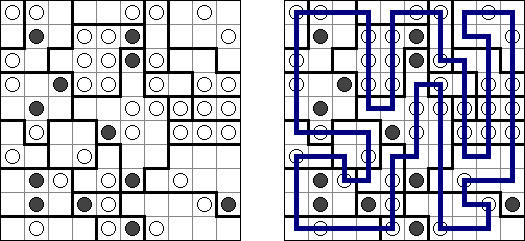
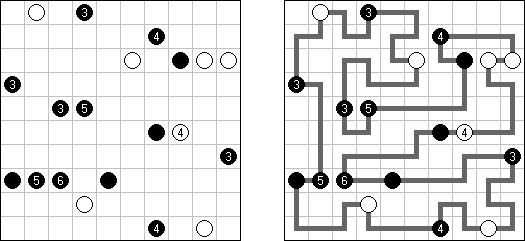
Masyu ("Shiroshinju Kuroshinju", "White Pearls and Black Pearls") es un pasatiempo lógico. El objetivo es unir los circúlos negros y los blancos con líneas rectas, verticales o horizontales, para formar un ciclo sin cortarse a sí mismo. Cuando el ciclo pasa por un círculo blanco, en la celda anterior o siguiente (o en ambas) ha de girar 90 grados. Cuando el ciclo pasa por un círculo negro, ha de girar 90 grados en la propia celda del círculo y tiene prohibido volver a girar en las celdas anterior y posterior.

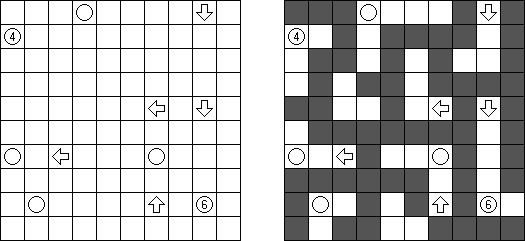
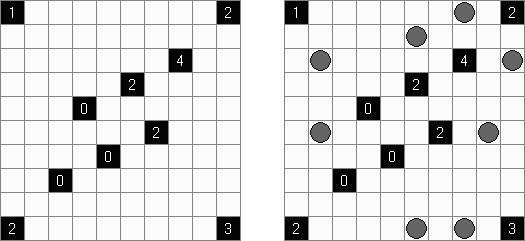
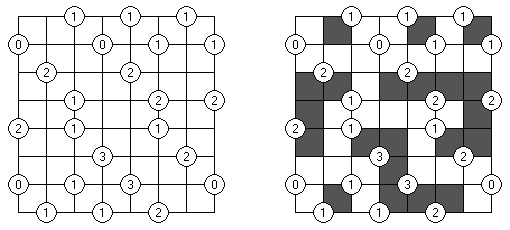
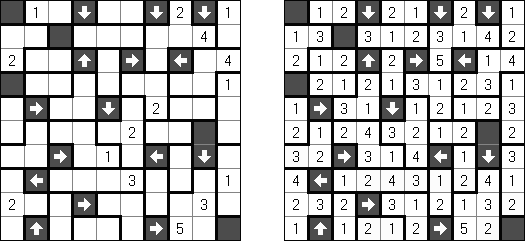
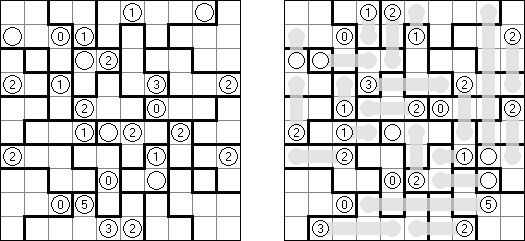
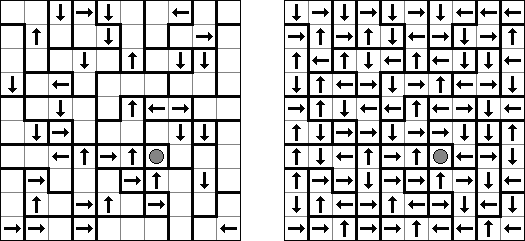
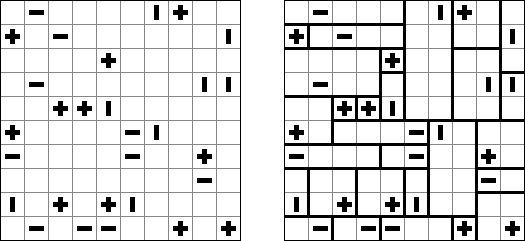
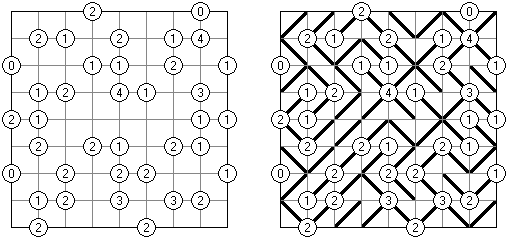
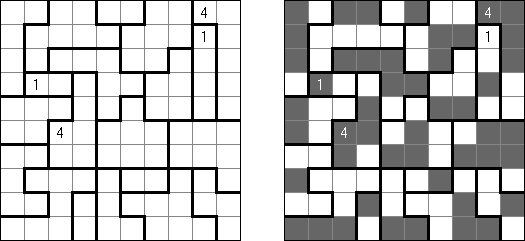
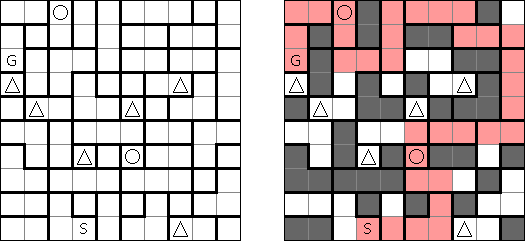
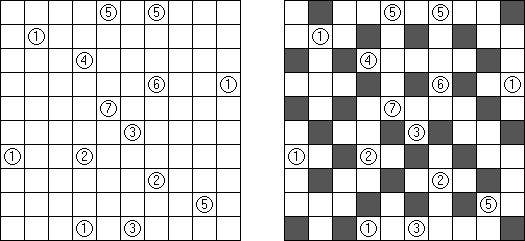
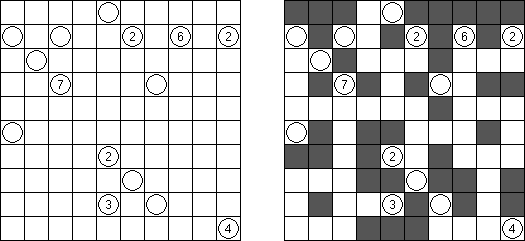
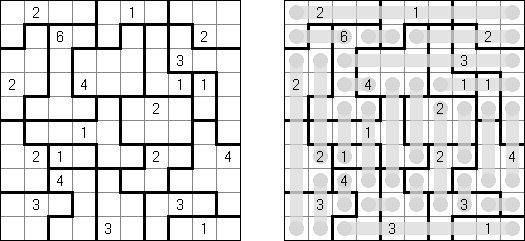
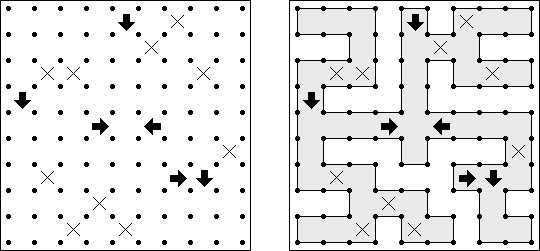
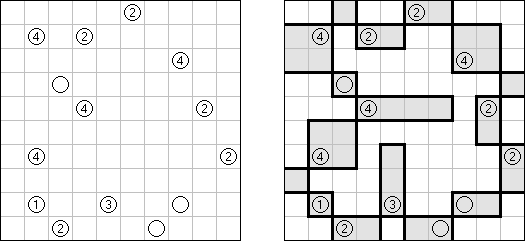
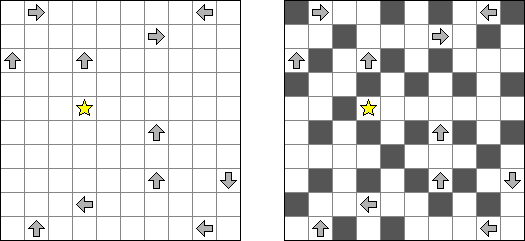
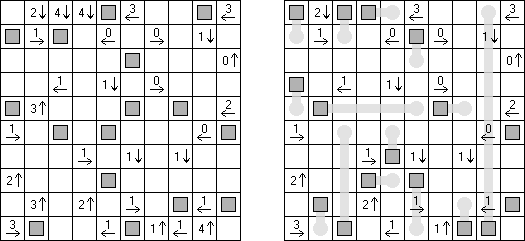
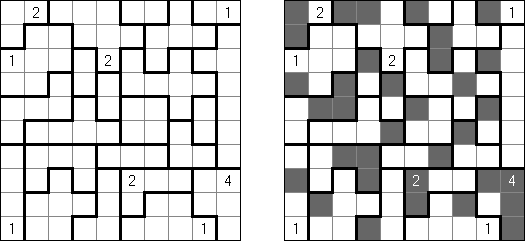
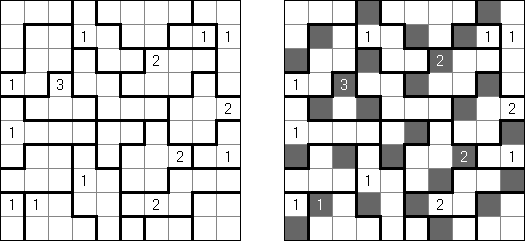
Akari ("Light Up", "Bijutsukan") es un pasatiempo lógico. La malla rectangular se forma de celdas blancas y negras; algunas celdas negras ya tienen números. El objetivo es situar "bombillas" en celdas blancas de manera que las bombillas iluminen la malla sin iluminarse mutuamente.

Las bombillas iluminan la malla en horizontal y en vertical hasta topar con un obstáculo de celda negra. El número en una celda puede ser de 0 a 4 indicando el número exacto de bombillas adyacentes a la celda sin tomar en atención las bombillas situadas en diagonal. Si no hay números en una celda, se puede situar cualquier número de bombillas en torno de esta.

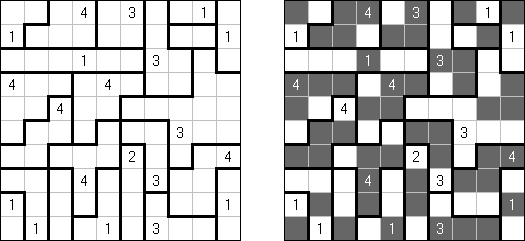
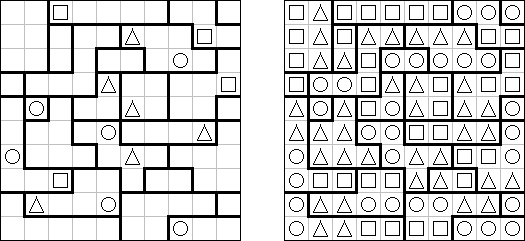
Fillomino ("Polyominous", "Allied Occupation") representa una cuadrícula del tamaño libre con números en unas de sus celdas. El objetivo es quedar la cuadrícula organizada en bloques. El bloque ha de tener tantas celdas cuantas indica el número en sus celdas. Los bloques del mismo tamaño no pueden tocarse en horizontal y en vertical. Las celdas sin números se puede incluir en los bloques para solucionar el pasatiempo.

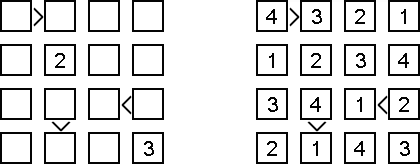
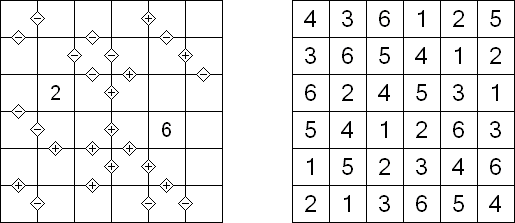
Futoshiki ("Hutoshiki", "Unequal") es un pasatiempo lógico númerico. La malla es un cuadrado con números en algunas celdas y signos "<" y ">" entre estas que indican la correlación de números adyacentes. El objetivo es rellenar las celdas libres con los números de manera que no se repitan los números en misma fila y columna.

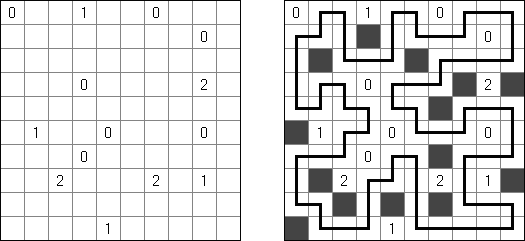
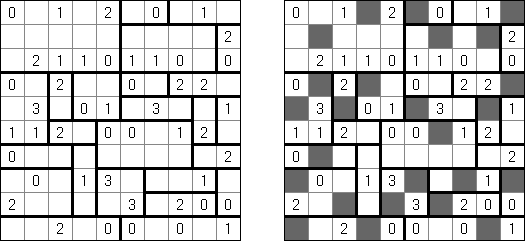
Kuromasu ("Kurodoko", "Where is Black Cells") es una malla rectangular con unos números en sus celdas. El objetivo es rellenar unas celdas de color negro según las reglas:

• Cada número indica el número de celdas "visibles" en vertical y en horizontal. Las celdas son visibles hasta toparse la mirada el margen de la malla o una celda negra.
• Las celdas con números no se rellenan de negro.
• Las celdas negras no pueden tocarse en vertical y en horizontal.
• Las celdas blancas forman el campo blanco conexo tocandose en vertical y en horizontal.

Nurikabe ("Cell Structure", "Islands in the Stream") es un pasatiempo lógico numérico. Tiene la palabra "nurikabe" su origen del japonés y denota un monstruo en forma de gran muro invisible que estorba el paso.

El objetivo es reconstruir un mapa con unas islas según las reglas:

• cada número indica el número de celdas ocupadas por la isla;
• las islas no pueden tocarse más que en diagonal;
• cada isla tiene solo un número en su descripción;
• por entre las islas hay un río;
• las celdas del río deben formar una única componente conexa;
• no pueden haber bloques 2 x 2 del río.

Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:

• All of the black cells must be connected.
• There cannot be any 2 x 2 blocks of black cells.
• All islands must be L-shaped and one cell wide. Two islands may not be connected.
• A circle represents a cell in which an "L" must bend.
• An island must have the same number of white cells as a number in a circle.
• An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.

Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:

• Cells with numbers are always white.
• No 2 x 2 cell area within the grid can contain all black cells.
• All the black cells form one contiguous region.
• A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.

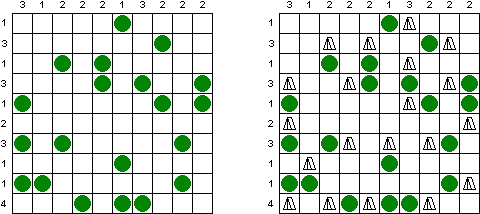
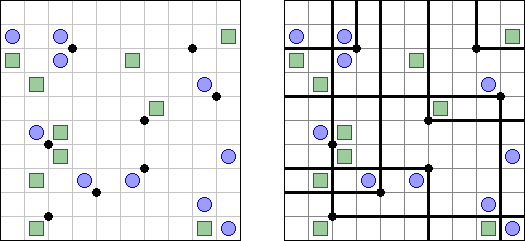
Tents ("Tents & Trees") es una cuadrícula con "árboles" en algunas celdas. El objetivo es situar tiendas cerca de los árboles según las reglas:

• El número de tiendas es igual al número de árboles.
• Cada tienda se situa cerca de su árbol en horizontal o en vertical y no en diagonal. Si condiciona la previa condición, no importa la posición de la tienda a otros árboles.
• Dos tiendas pueden encontrarse en celdas adyacentes, incluso en diagonal.
• Los números al lado y de arriba indican el número de tiendas en la fila o en la columna correspondiente.

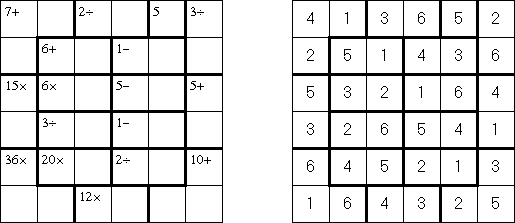
Calcudoku ("KenKen", "KENKEN", "KenDoku", "Square Wisdom") es un pasatiempo lógico, matemático. El objetivo es rellenar la cuadrícula con los números de manera que no se repitan en la misma fila y misma columna. El número en el rincón de cada bloque subrayado es el resultado de una operación aritmética con los números de este bloque. A diferencia de Sudoku Asesino (Killer Sudoku) pueden repetirse los números en el bloque.

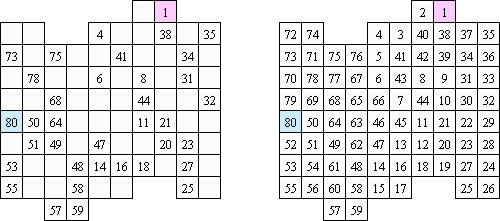
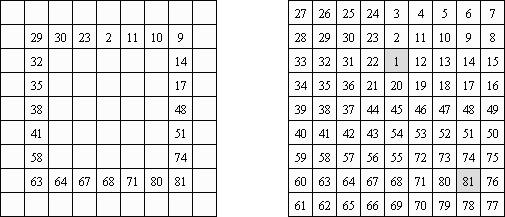
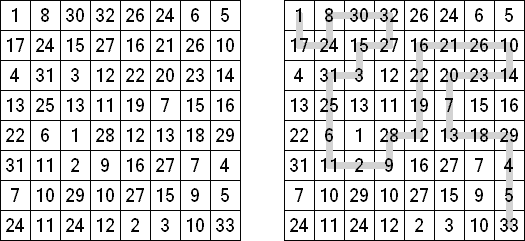
Hidato (del hebreo "mi rompecabezas"; "Hidoku") fue inventado por Gyora Benedek, un matemático israelí. El puzzle es una cuadrícula de forma libre, rectangular o cuadrada como regla. La tarea es llenar la cuadrícula de tal manera que los números consecutivos estén siempre conectados en diagonal, vertical o horizontal. Cada rompecabezas ya tiene los números máximos y mínimos. El campo de juego puede contener otros números para facilitar el proceso y asegurar la única solución.

Numbrix es un pasatiempo lógico. El objetivo de este juego consiste en ir llenando con números los espacios en blanco dentro de un tiempo, de modo que sigan un camino numérico correlativo. El camino puede ser horizontal o vertical, pero nunca diagonal.

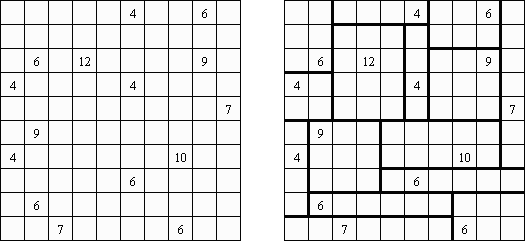
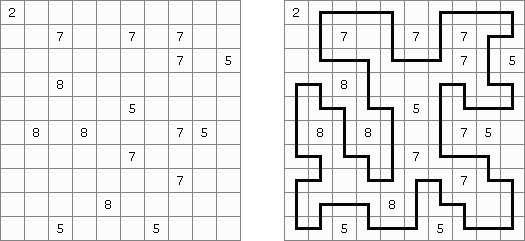
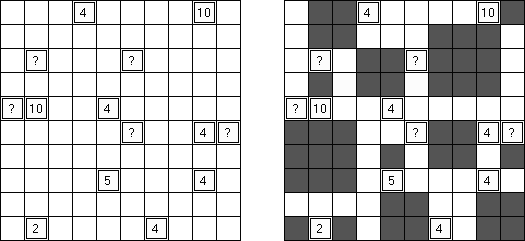
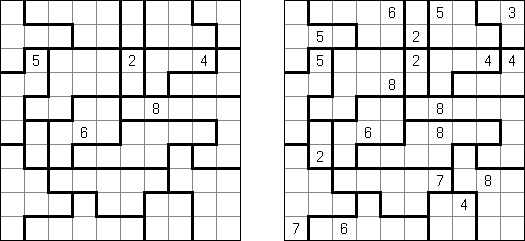
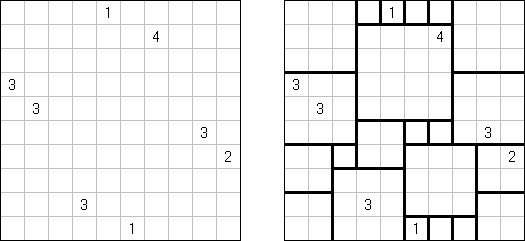
Shikaku ("Divide by Squares", "Divide by Box", "Number Area") es un puzzle lógico. El pasatiempo presenta un tablero cuadrado de tamaño libre con algunos números. La tarea es trazar unas líneas repartiendo el tablero en rectángulos y cuadrados de tal manera que cada región contenga un y solo un número que indique la cantidad de celdas de dicho rectángulo o cuadrado (su superficie).

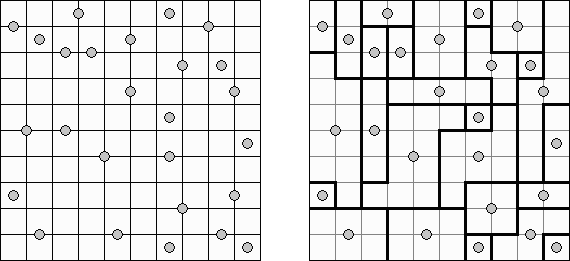
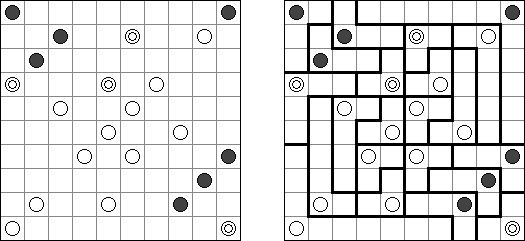
Galaxies ("Tentai Show") ofrece una malla rectangular (generalmente cuadrada), con algunos círculos (blancos y negros) dispuestos en el interior o en la separación de diversas celdas. Se trata de parcelar la malla en bloques (habitaciones, no necesariamente rectangulares, sino simétricamente estrelladas), según las siguientes reglas:

• Cada habitación ha de contener un y sólo un círculo.
• La habitación ha de ser simétrica respecto del centro del círculo que contiene.
• Al sombrear las celdas correspondientes a habitaciones con círculo negro se obtiene un dibujo.

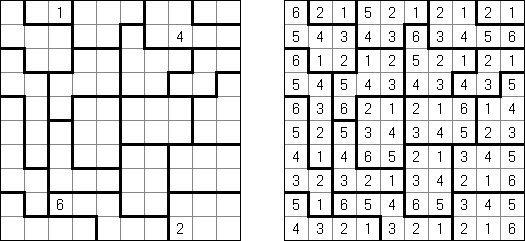
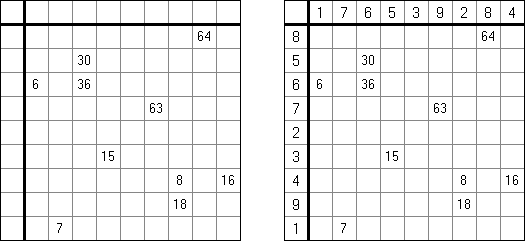
Rascacielos ("Skyscrapers") es un tipo de pasatiempo lógico. Hay que llenar un cuadrado con números de modo que en cada línea y en cada columna no se repitan los números. Llenando el cuadrado hay que usar los números-llaves y considerar que en cada celda dentro del cuadrado hay una casa el número de pisos de la cual es igual al número en la celda, y que los números fuera del cuadrado muestran el número de casas en su línea o columna correspondiente.

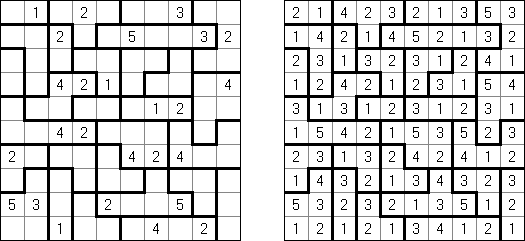
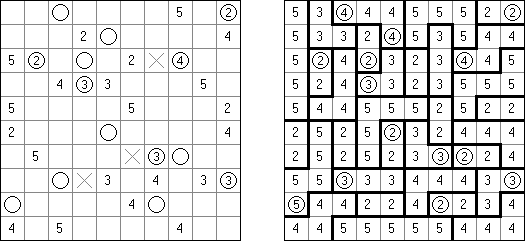
Hakyuu ("Ripple Effect", "Hakyuu Kouka", "Hakyukoka", "Seismic") es un pasatiempo lógico. Representa una cuadrícula dividida en bloques ("cuartos") en unos de los cuales se encuentran números. Hay que rellenar las celdas con números de manera que en cada bloque se encuentren los números de 1 al número de celdas en el bloque. Si tiene una fila o columna dos números iguales, el número de celdas entre estas es más o igual a estos números. Por ejemplo, si hay en una columna dos celdas con el número 5, deben separarse por lo menos cinco celdas con otros números.

Grand Tour es un pasatiempo lógico en que uno tiene que construir una línea cerrada por todos los puntos de una cuadrícula de manera que no se interseque y no se toque a sí misma. Para evitar multiples soluciones, tiene el pasatiempo unos puntos unidos con líneas ya.

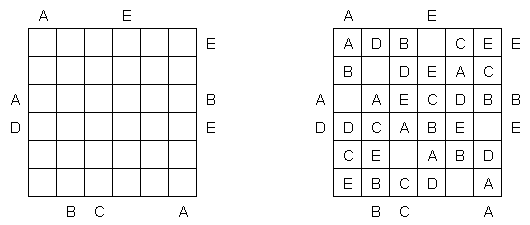
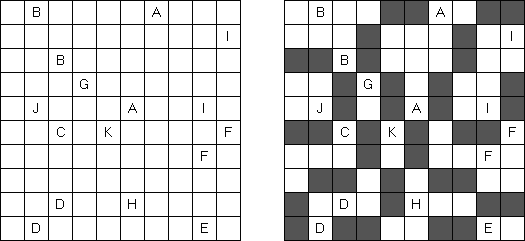
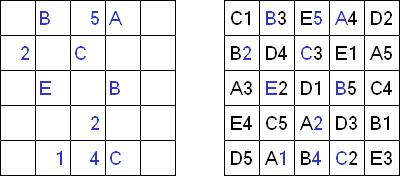
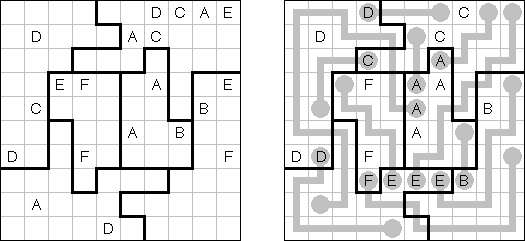
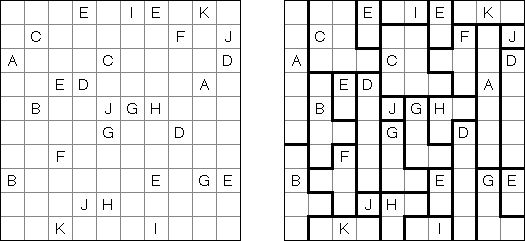
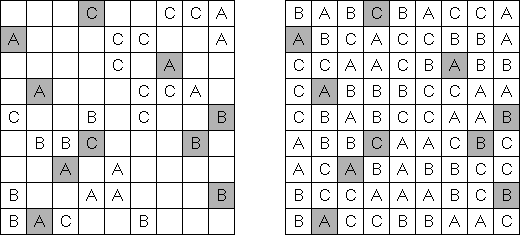
ABC ("Easy as ABC", "ABC End View", "Last Man Standing") es un pasatiempo lógico con letras. Hay que rellenar la cuadrícula con letras latinas (por ejemplo, de A a E) sin repetir los símbolos en la misma línea o fila. Se puede dejar vacías unas celdas. La letra en el borde de la cuadrícula es la primera letra de la línea (columna).

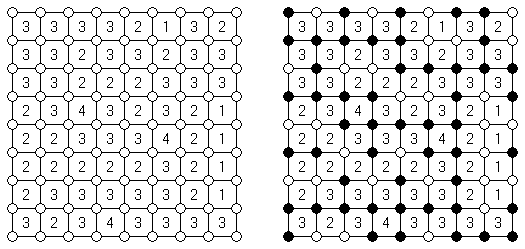
Nubes ("Clouds", "Rain Clouds", "Radar") es un variante del pasatiempo "Batalla naval". En una cuadrícula de forma libre hay que situar unos rectángulos ("nubes") que no se toquen aún sus puntas. Los números fuera de la cuadrícula significan la cantidad de celdas ocupadas con nubes. El número y tamaño de nubes no se dan pero los lados de rectángulos no deben ser menos de dos celdas.

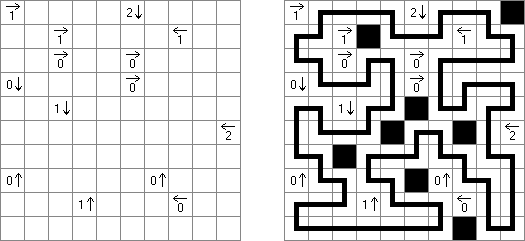
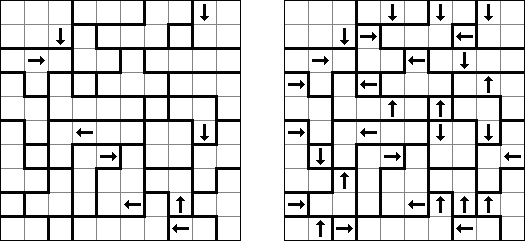
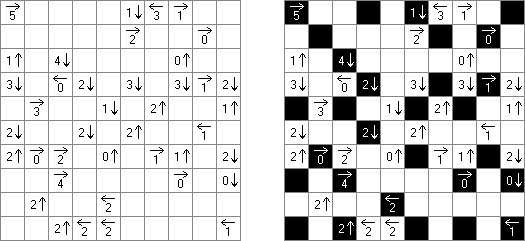
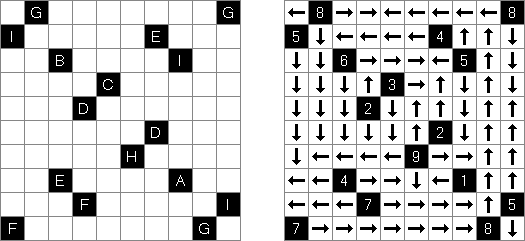
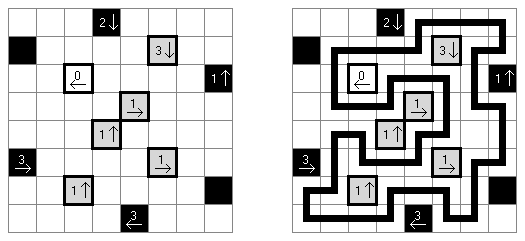
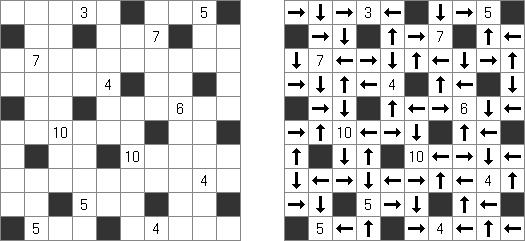
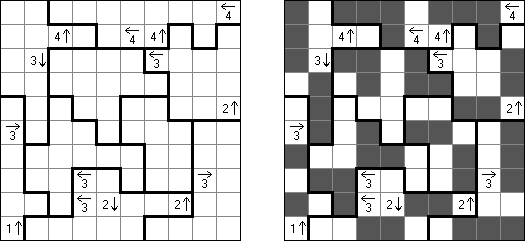
Yajilin ("Arrow Ring", "Straight and Arrow") es un pasatiempo lógico de forma cuadrada o rectangular. El pasatiempo representa celdas con flechas y números que ayudan situar unas celdas negras en la cuadrícula. La tarea es dibugar una línea cerrada que no se atraviese a si misma y no entre las celdas negras o con flechas. The grid may contain gray cells that can not be part of the loop.

• Los números en las celdas significan la cantidad de celdas negras en la columna o en la fila según la dirección de la flecha. Las celdas con flechas no se tomen como las negras.
• Si en la celda no hay flecha ni es negra, hay que llenarla con línea.
• Los números en las celdas significan la cantidad de celdas negras. Es que, si tiene una celda el número "3" y una flecha a la izquierda, lo significa que la fila a la izquierda de la celda tiene tres celdas negras.
• Las celdas negras no pueden tocarse en vertical y en horizontal.
• El campo puede tener unas celdas negras no indicadas con ningunas flechas.

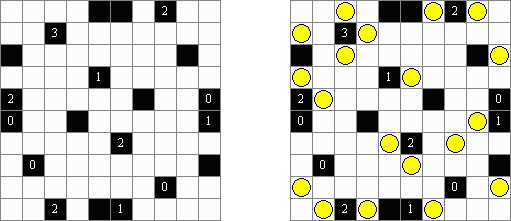
Buscaminas ("Minesweeper") es un juego conocido a cada usuario de Microsoft Windows. Hay que poner unas "minas" en celdas libres usando los números claves. Cada número clave significa la cantidad de celdas vecinas con minas. Cada celda puede tener una mina y la celda con número no puede tener minas.

Minesweeper Battleships (also known as "Battlemines") combines Battleships puzzle with Minesweeper game found on many computers. The aim is to locate the position of the fleet in the grid. The ships do not touch each other, not even diagonally. A cell with a number indicates how many ship pieces are adjacent to it. Ships are not allowed on the numbered cells.

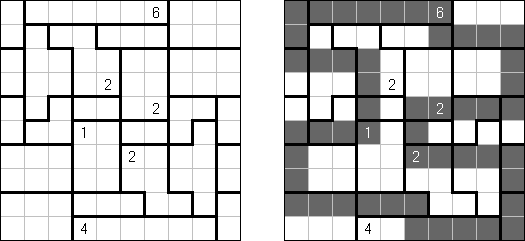
Heyawake (se traduce de japonés como "cuartos separados") es un rompecabezas lógico. Representa una cuadrícula dividida en unos bloques ("cuartos"). En unos bloques hay números que significan la cantidad de celdas negras en cada bloque. Si un bloque es vacío puede tener cualquiera cantidad de celdas negras.

• Las celdas negras no pueden tocarse en vertical y en horizontal (en diagonal sólo).
• Todas las celdas blancas se unen en horizontal o en vertical.
• Una línea continua no puede atravesar más de dos "cuartos".

Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten") representa una cuadrícula de diez celdas en horizontal. Hay que rellenar la cuadrícula de tal modo que cada fila tenga números de 0 á 9. Números en columnas pueden repetirse. El número debajo de la cuadrícula significa la suma de los números en la columna. Los números en las celdas adyacentes (aún en diagonal) deben ser diferentes.

Centena ("Hundred") representa un cuadrado con números en cada celda. Hay que situar unos números adicionales para que la suma de números en cada línea y cada columna sea igual a 100.

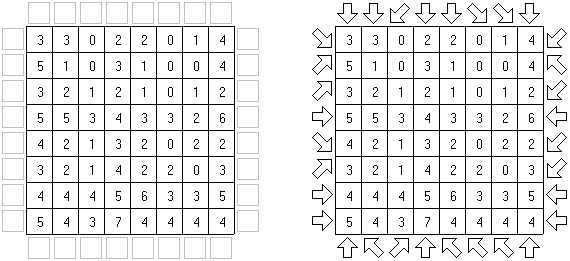
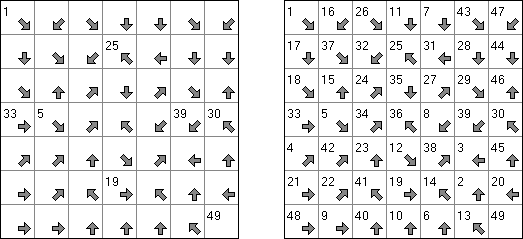
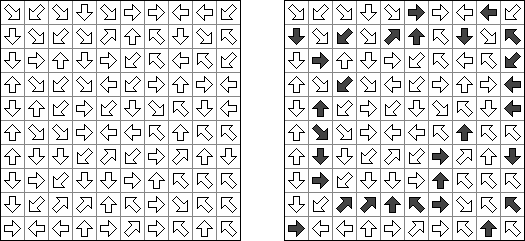
Flechas ("Arrows") es un variante de pasatiempo lógico. Representa una cuadrícula o un cuadrado con números en cada celda. La tarea es situar flechas fuera de la cuadrícula. Cada flecha debe apuntar, por lo menos, a una celda con número. Cada número indica la cantidad de flechas que deben apuntar a la celda.

Mathrax es un variante de pasatiempo lógico. Hay que llenar un cuadrado con números de tal modo que en cada línea y en cada columna no se repitan los números. La cuandrícula puede contener ya algunos números. En los puntos donde las líneas se cruzan, unos círculos con reglas adicionales se situarían:

• Número y signo de operación aritmética (adición, sustración, multiplicación, división): el número en el círculo es el resultado de la operación aritmética sobre la pareja de números el las celdas adyacentes al círculo y adherentes en diagonal.
• La letra "E" latina: en las celdas adyacentes al círculo todos los números son pares ("E" de "even" (par) inglés).
• La letra "O" latina: en las celdas adyacentes al círculo todos los números son impares ("O" de "odd" (impar) inglés).

Str8ts ("Straights") es un pasatiempo lógico inventado por Jeff Widderich de Canadá. La cuadrícula en forma de un cuadrado se compone de celdas negras y blancas. Hay que situar números en las celdas blancas para formar unas secuencias de números (el ordén numérico no es importante: por ejemplo, 1-3-4-2) en espacios blancos. En cada línea y en cada columna los números en celdas blancas y negras no deben repetirse. Los números en celdas negras no forman parte de secuencias de números.

Buscalíneas ("Linesweeper") es un pasatiempo lógico parecido a "Buscaminos" ("Minesweeper"). Representa una cuadrícula o cuadrado con números en algunas celdas (de 0 a 8). Hay que dibujar una línea cerrada que no se atraviese a si misma y no entre las celdas con números. El número en la celda significa la cantidad de celdas adyacentes a la celda con número y atravesadas por la línea.

Binairo ("Binary Puzzle", "Takuzu", "Tohu wa Vohu") es un pasatiempo lógico en que las cifras "0" y "1" se usan. La tarea es llenar el campo cuadrado o rectangular con estas dos cifras según las reglas:

• Cada línea y cada columna pueden contener el número igual de cifras "1" y "0" (ó en una cifra más para las cuadrículas con el número de celdas impar).
• La misma cifra puede contenerse solo en dos celdas consecuentes y no más.
• Cada línea y cada columna debe ser única.

Paredes ("Walls") es un pasatiempo lógico inventado por Naoki Inaba de Japón. La tarea es situar unas líneas horizontales y verticales en las celdas blancas de modo que lo largo de todos los rayos que se inician de la celda negra sea igual al número en la celda.

Dominosa ("Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") es un pasatiempo lógico basado en fichas de dominó. En el campo de juego hay solo unos números y su tarea es restituir los linderos por entre las fichas.

Patchwork ("Tatami") representa una cuadrícula dividida en regiones iguales ("cuartos"). Hay que llenar cada cuarto con las cifras de "1" a la cifra que sea igual al número de celdas en la región. Cada línea y cada columna deben contener la cantidad igual de cada tipo de números. Las celdas adyacentes en horizontal y en vertical no pueden contener los mismos números.

En algunos variantes de este pasatiempo se usan letras en vez de números. Cross+A puede solucionar los pasatiempos de ambos tipos: tanto con letras como con números.

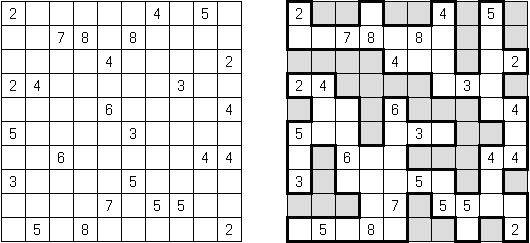
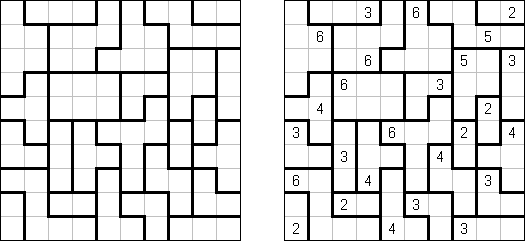
Cnosos ("Knossos"; "Cnosos" es un palacio en Creta asi como la ubicación del laberinto en que Minotauro fue encerrado) representa un campo de juego rectangular o cuadrado con números en unas de sus celdas. Hay que dividir la cuadrícula en unos regiones (“cuartos” de modo que en cada regíon sea un número) que es igual al perimetro de la región.

Rekuto ("Recto") es un pasatiempo lógico de forma cuadrada o rectangular con números en unas celdas. La tarea es trazar unas líneas repartiendo el tablero en rectángulos y cuadrados de tal manera que cada región contenga un y solo un número que indique la suma de lo alto y lo ancho de la región.

Vecinos ("Neighbours") es un pasatiempo lógico con el tablero de forma libre. En unas celdas hay números o signos de interrogación. Hay que dividir el tablero en regiones con la cantidad iguál de celdas. Cada región puede contener sólo una celda con un número o interrogación: el número significa la cantidad de "vecinos" de la región dicha. Las regiones vecinas son las con la raya común. Las regiones con interrogaciones pueden tener cualquier número de "vecinos".

Cuatro vientos ("Four Winds", "Line Game") es un pasatiempo lógico de forma cuadrada o rectangular con celdas negras y blancas. La tarea es trazar unas líneas rectas de manera que salgan de celdas negras y atraviesen las celdas blancas. El número en cada celda negra significa la cantidad de celdas blancas con líneas que salen de esta. Las líneas no pueden atravesarse.

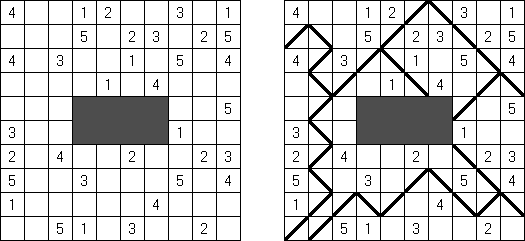
Shakashaka ("Proof of Quilt") es un pasatiempo lógico de forma cuadrada o rectangular. El tablero se forma de celdas blancas y negras. Unas celdas negras pueden contener números de 0 a 4. La tarea es situar unos triángulos negros en celdas blancas para formar cuadrados y rectángulos blancos. No hay que llenar todas las celdas blancas. Las regiones blancas pueden ser horizontales, verticales o diagonales, pero no deben tener lados comunes. El número en cada celda negra es la cantidad de triángulos adyacentes.

Kakurasu ("Index Sums") es un pasatiempo de forma cuadrada o rectangular para llenar con celdas negras y blancas. Los números a la izquierda y en la parte superior del campo de juego significan las sumas de "pesos" de celdas negras en líneas y columnas. Los números a la derecha y de abajo significan el "peso" de celdas negras en líneas y columnas (el cuadrado negro en la línea o columna primera "pesa" 1, en la línea o columna segunda "pesa" 2, etc.).

Mochikoro ("Mochinuri") representa un tablero cuadrado o rectangular con números en unas celdas. La tarea es situar unas celdas negras y blancas para formar "islas" cuadradas o rectangulares de celdas blancas.

• Cada "isla" blanca puede contener no más de una celda con número; el número significa la cantidad de celdas blancas en la región.
• Unas "islas" son libres de celdas con números.
• Las regiones blancas no tengan lados adyacentes, pero todas estas regiones deben tocarse en diagonal.
• El tablero no debe contener cudrados de 2 a 2 celdas negras.

Puertas ("Seethrough", "Doors", "Open Office") es un pasatiempo lógico de forma cuadrada o rectangular en que cada celda es un cuarto. La tarea es cerrar o abrir “puertas” de cuartos. Las puertas abiertas permiten mirar de cuarto a cuarto o por dentro de algunos cuartos. El número en una celda significa el número de cuartos que se vean de este a excepción del mismo cuarto. No deben dejarse unas partes isoladas de la cuadrícula: es que de cada cuarto hay acceso a otro.

Faros ("Lighthouses") es un pasatiempo lógico con celdas negras ("faros"). El número en estas celdas significa el número de buques iluminados por el faro. Un faro ilumina un buque si están en una línea o una columna, no importe hay otros buques o faros entre estos o no. Cada buque se ilumina por lo menos por un faro. Hay que situar los buques de manera que no toquen a faros o otros buques aún en diagonal.

Lighthouse Battleships combines Battleships with Lighthouses puzzle. A cell with a number is a lighthouse, and it indicates the total number of ship pieces that are in the same row or column as the lighthouse. Ships can not touch the lighthouses, not even diagonally.

Tapa es un pasatiempo inventado por Serkan Yürekli de Turquía. Representa un campo de juego cuadrado o rectangular de celdas blancas. La tarea es llenar unas celdas de negro para observar las reglas:

• Las celdas negras no pueden tocarse en vertical y en horizontal.
• No puede formar regiones de 2 a 2 celdas negras.
• Celdas blancas y con interrogaciones se dejan blancas.
• Cada número significa un grupo sólido de celdas negras agrupadas en torno de la celda blanca con este número; dos grupos de celdas negras deben separarse por una celda blanca por lo menos.
• El signo de interrogación significa cualquier número más de 0.
• Posiciones de números o su arreglo dentro de las celdas no importan.

Fobidoshi ("El cuatro está de más", "Forbidden Four") es un pasatiempo inventado por Naoki Inaba de Japón. El pasatiempo representa un campo cuadrado o rectangular con círculos en algunas celdas. Hay que llenar las celdas vacías con círculos de modo que se toquen en horizontal o vertical. No se puede situar más de tres círculos consecutivos en horizontal o en vertical.

La isla ("Island", "Tents Island", "Airando") es un rompecabezas lógico inventado por el japonés Naoki Inaba. Representa una cuadrícula en algunas casillas de la cual hay números. Hay que pintar de negro las casillas de modo que las casillas que queden blancas formen una isla. Las casillas con números forman parte de la isla. El número muestra cuántas casillas blancas sin números se pueden obtener moviéndose por la superficie desde una casilla numerada horizontal y verticalmente (hasta que otra casilla con numerada bloquee el movimiento).

Dominion es una cuadrícula con letras en algunas casillas. El objetivo es pintar de negro algunas casillas de acuerdo con las siguientes reglas:

• Las casillas negras se pueden añadir en el campo sólo en pares, es decir, cada dos nuevas casillas negras debe tocarse horizontal o verticalmente (tales pares de células son llamadas "el dominó").
• Las fichas del dominó pueden estar en contacto entre sí sólo en diagonal.
• Las casillas con letras deben quedar blancas.
• Las casillas negras dividen el campo en varias áreas blancas. Dentro de la misma área todas las casillas blancas deben estar en contacto entre sí ya sea horizontal o verticalmente.
• Las casillas con la misma letra pertenecen a la misma área blanca.
• No puede haber una zona blanca sin una casilla con letra.

Tren es un rompecabezas lógico inventado por el japonés Shinichi Aoki. El nombre japonés del problema lógico se traduce como "aparcamiento" (cada pieza es un coche, toda la cuadrícula es el aparcamiento). El rompecabezas consiste en una cuadrícula rectangular o cuadrada con números en algunas casillas. En la cuadrícula hay que colocar bloques de 1 x 2 y 1 x 3. Cada número debe ser parte de un bloque. Este número indica el número de casillas por el cual se puede mover el bloque. El bloque sólo se puede mover en la dirección del lado corto.

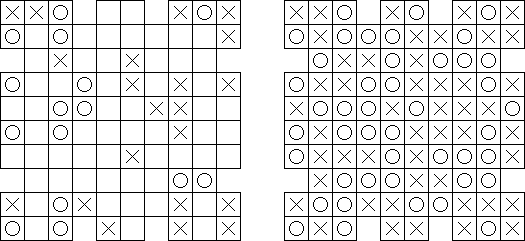
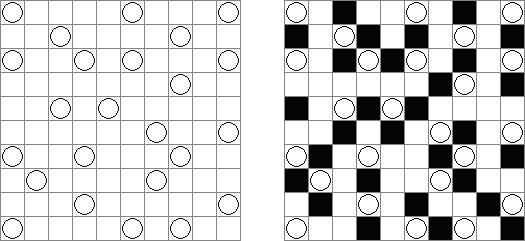
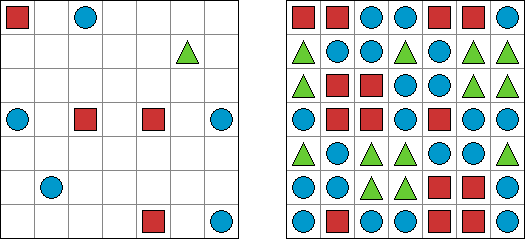
Tres en una fila ("No Four in a Row") es una retícula de cualquier forma. En algunas casillas de la retícula hay "O" y "X". Hay que rellenar las casillas restantes de manera que en horizontal, en vertical o diagonal no haya más de tres signos idénticos seguidos.

Corral ("Bag", "Cave") es un campo cuadrado o rectangular con unos numeros en sus celdas. Hay que trazar una línea cerrada al rededor de todos números. Cada número significa la cantidad de celdas que se vean de esta celda en horizontal y en vertical dentro de la línea cerrada con la misma celda con número.

Cuatro casillas ("Foseruzu", "Four Cells") es un rompecabezas de lógica que representa una retícula cuadrada o rectangular con números en algunas casillas. Hay que dividir la retícula en bloques de 4 casillas. El número indica cuántos lados de la casilla contienen elementos de límites entre bloques (el límite exterior de la casilla también se incluye). Un bloque puede contener cualquier cantidad de números (o no contener ninguno).

CincoCasillas ("Faibuseruzu", "Five Cells", "Solomon's Keep"): la retícula está dividida en bloques de 5 casillas.

Sutoreto ("Sutoretokurosu", nombre inglés "Straight Cross" alterado por la pronunciación japonesa) es un juego de lógica inventado por Naoki Inaba de Japón. El juego representa una retícula rectangular o cuadrada con casillas blancas y negras. Algunas casillas blancas son numeradas. Hay que llenar de números las casillas blancas que quedan de modo que entre las casillas negras tanto en horizontal como en vertical se formen conjuntos de números consecutivos, pero no necesariamente seguidos (por ejemplo, 2-3-4 o 5-4-7-6).

Renban una cuadrícula dividida en áreas de forma y tamaño libres. Hay que llenar la cuadrícula con números de modo que cada número se use sólo una vez en cada fila, en cada columna y en cada bloque. Todos los números del área son una serie de números consecutivos, pero no necesariamente en orden ascendente o descendente (por ejemplo: 5-3-4).

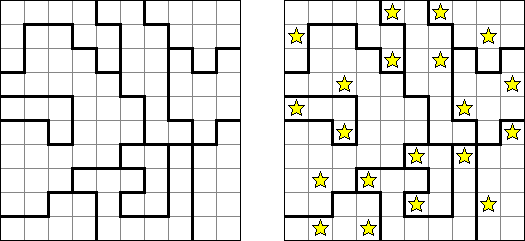
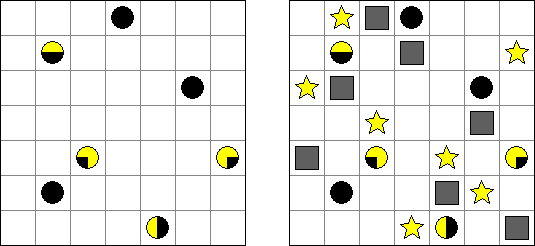
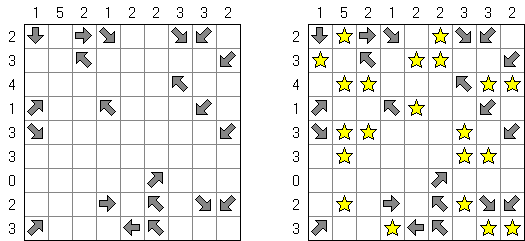
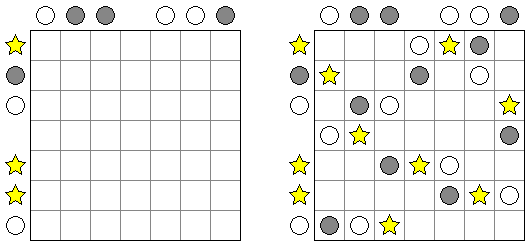
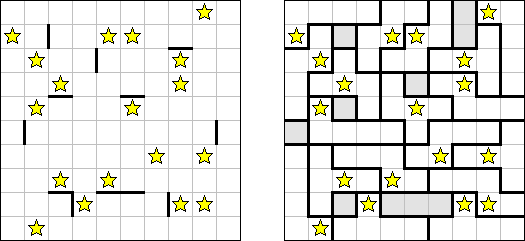
Buraitoraito (nombre inglés "Bright Light" alterado por la pronunciación japonesa) es un rompecabezas inventado por Naoki Inaba de Japón. Representa una retícula cuadrada o rectangular con casillas blancas y negras. Hay que colocar estrellas en las casillas blancas de modo que cada número en una casilla negra corresponda al número de las estrellas visibles desde la casilla horizontal y verticalmente. "La vista" se extiende hasta que alcance el borde del campo o tropiece con otra casilla negra.

Irasuto (nombre inglés "Illustration" alterado por la pronunciación japonesa) es un rompecabezas lógico inventado por Naoki Inaba de Japón. El juego representa una rejilla rectangular o cuadrada con las casillas en blanco y negro. En algunas casillas de la cuadrícula hay números. Hay que colocar las casillas negras y blancas observando las siguientes reglas:

• El número en una casilla blanca indica cuántas casillas blancas "se ven" desde la casilla vertical y horizontalmente. "La vista" se extiende hasta tropezar con una casilla negra u otra casilla blanca con número.
• El número de casillas negras indica cuántas casillas negras "se ven" de la casilla vertical y horizontalmente. "La vista" se extiende hasta tropezar con una casilla blanca u otra casilla negra con número.

Suguru ("Number Blocks") es un rompecabezas lógico inventado por Naoki Inaba de Japón. Es una rejilla cuadrada o rectangular dividida en áreas. Hay que llenar todas las casillas de los números de modo que cada área contenga los números del 1 al número de casillas en el área. Las casillas con números iguales no pueden tocarse en horizontal, vertical o diagonal.

Trinudo es un rompecabezas lógico cuadrado o rectangular. En algunas casillas de la cuadrícula hay números. Hay que dividir la cuadrícula en bloques de una, dos o tres casillas. Los bloques del mismo tamaño no deben tocarse horizontal o verticalmente. Cada número indica cuántas casillas contiene el bloque al cual pertenece el número.

Creek ("Kuriku") es un rompecabezas lógico que representa una rejilla cuadrada o rectangular; en las intersecciones de las líneas se pueden colocar círculos con los números de 0 a 4. El número indica cuántas casillas negras son adyacentes al círculo. Debe colocar las casillas en blanco y negro, de tal manera que todas las casillas blancas se toquen en vertical o en horizontal.

Gappy es un pasatiempo lógico que se presenta como una malla cuadrada. Hace falta colocar las celdas negras de manera que en cada línea y en cada columna se encuentren dos celdas negras. Las celdas negras no deberán contactar ni hasta con sus ángulos. Las cifras en los extremos de la malla designan el número de las celdas blancas entre las celdas negras en la línea o la columna.

Norinori es una variedad del pasatiempo lógico. Viene representado por una malla rectangular o cuadrada, dividida en regiones de forma libre. Hace falta pintar en negro dos casillas en cada región. Las casillas pintadas en negro han de formar bloques del tamaño de 2 x 1 o 1 x 2 (fichas del dominó), sin que importen fronteras de las regiones. Dos bloques de color negro no podrán contactar (pero sí, podrán hacerlo con sus ángulos).

Yonmasu ("Yonmasubunkatsu") es un pasatiempo lógico inventado por Naoki Inaba de Japón. La tarea viene representada por una malla de forma rectangular o cuadrada. Algunas celdas contienen círculos. Hay que dividir la malla en regiones de cuatro celdas de modo que cada región tenga un círculo.

Ladrillos ("Bricks") es una especie de rompecabezas lógico. Hay que llenar con números la cuadrícula de modo que no se repitan en ninguna fila y en ninguna columna. En cada ladrillo una número es par y el otro es impar.

Cadena de números ("Number Chain") es un rompecabezas con números inventado por Leonid Mochalov de Rusia. Se trata de una cuadrícula rectangular o cuadrada, en la cual cada célula contiene un número. En el ángulo superior izquierdo de la cuadrícula está el número 1, en el ángulo inferior derecho está N; las células restantes contienen números arbitrarios de 1 a N. Hay que abrir el camino desde el ángulo superior izquierdo de la cuadrícula al ángulo inferior derecho de modo que la línea quebrada pase a través de N células con números que no se repitan.

Kapetto ("Settokapetto" - denominación inglesa "Set Carpets" tergiversada por la pronunciación japonesa) es un pasatiempo lógico inventado por Naoki Inaba de Japón. La tarea está representada por una malla rectangular o cuadrada, algunas celdas de la cual contienen números. Hace falta ubicar las regiones rectangulares en la malla de manera que cada región tenga un solo número. El número significa la superficie de la región. La malla podrá tener celdas que no pertenecen a ninguna de las regiones.

Renkatsu es un rompecabezas lógico inventado por Naoki Inaba de Japón. Es una rejilla cuadrada o rectangular completamente llenada de números. Hay que dividir la cuadrícula en áreas de manera que cada área contenga números de 1 a N, donde N es el tamaño del área.

Eulero ("Cuadrado greco-latino", "Cuadrado de Euler") es un rompecabezas con letras y números. Hay que llenar la cuadrícula con símbolos de modo que se cumplan las siguientes condiciones:

• En cada célula hay una letra y un dígito.
• En cada fila y cada columna de cada letra y cada dígito se encuentran sólo una vez.
• Cada combinación de letra y número en el cuadrado se encuentra sólo una vez.

Anraikumozaiku (la frase inglesa "Unlike Mosaic" deformada por la pronunciación japonesa) - un rompecabezas lógico creado por Naoki Inaba del Japón. Se trata de una cuadrícula rectangular o cuadrada, en la cual algunas células contienen círculos. Hay que dividir la cuadrícula en regiones rectangulares de manera que cada región contenga un círculo. Las células negras no pertenecen a ninguna de las regiones. Las regiones que contienen el mismo número de células no pueden tocar vertical ni horizontalmente.

Kurotto ("bloques negros" en japonés) es una especie de rompecabezas lógico. Se trata de una cuadrícula rectangular o cuadrada, en la cual algunas células contienen círculos (en blanco o con números). Hay que colocar las células blancas y negras observando las siguientes condiciones:

• Una célula con un círculo no puede ser pintada de negro.
• Las células negras forman regiones en las cuales las células están en contacto en horizontal y en vertical.
• El número dentro del círculo es igual a la superficie de todas las regiones de células negras que se tocan horizontal y verticalmente con la célula correspondiente.
• Si el círculo no contiene números, tal célula puede ser adyacente de una región de células negras de cualquier tamaño.

Tasukuea (traduciendo de japonés: "encuentra cuadrados") – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, en algunas celdas de la cual se encuentran números o signos de interrogación. Hace falta situar casillas blancas y negras, cumpliendo las siguientes reglas:

• Una celda con el número o signo de interrogación no puede ser pintada de negro.
• Las casillas negras han de formar zonas de forma cuadrada.
• Las zonas de casillas negras no pueden tocarse en horizontal o vertical.
• El número es la superficie de todas las zonas de casillas negras, que tocan a esta celda en horizontal y en vertical.
• A la celda que contiene el signo de interrogación la pueden tocar zonas de casillas negras de cualquier superficie (pero al menos una casilla negra).
• Todas las casillas blancas han de formar un campo blanco unido, o sea tocarse en horizontal o en vertical.

Batalla de estrellas ("Star Battle") – es un pasatiempo lógico, que representa una malla cuadrada con regiones de forma aleatoria. Hace falta situar en la malla los círculos (“estrellas”) de tal forma que cada fila, cada columna y cada región contengan la misma cantidad de “estrellas”. Las celdas con círculos no deben tocar una a la otra incluso en diagonal.

Araf (traduciendo de turco "purgatorio"; otro nombre – "Aidabeya") – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, algunas celdas de la cual tienen números. Es necesario dividir la malla en regiones de tal forma que cada región contenga dos números. La superficie de una región debe tener el valor intermedio entre estos dos números. Por ejemplo, si una región contiene números 2 y 5, su superficie debe ser igual a tres o cuatro celdas.

Kabingurodo (denominación inglesa "Curving Road" tergiversada por la pronunciación japonesa) es un pasatiempo lógico inventado por Naoki Inaba de Japón. La tarea va representada por una malla rectangular o cuadrada, en algunas celdas de la cual hay círculos. Hace falta distribuir en la malla las casillas negras, observando las siguientes reglas:

• Las casillas con círculos no podrán tener el color negro.
• Las casillas negras no podrán contactar horizontal y verticalmente, solo podrán hacerlo en diagonal.
• Todas las casillas blancas constituyen un campo blanco único, es decir contactan vertical u horizontalmente.
• Cualquier vía que podrá ser trazada por las casillas blancas de un círculo al otro, ha de girar dos veces, como mínimo.

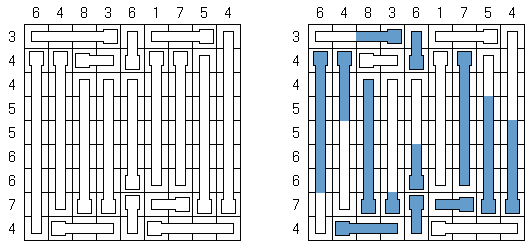
Termómetros ("Thermometers") – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, encima de las celdas de la cual están situados los termómetros. Los números a los lados de la malla señalan cuantas secciones dentro de los termómetros están llenos de líquido en sus correspondientes filas y columnas. Un termómetro se llena con el líquido empezando del depósito (parte convexa), independientemente de la orientación del termómetro en el espacio.

Serpiente ("Snake", "Tunnel") – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, dentro de la cual se indican los puntos inicial y final de la “serpiente”. Hace falta pintar de negro varias celdas de tal forma que formen una línea ininterrumpida entre estos dos puntos. La “serpiente” no puede tocar a sí misma, incluso en diagonal. Los números a los lados de la malla indican cuantas celdas negras en total hay en cada fila y columna correspondiente de la malla.

Peintoeria (una distorsión con pronunciación japonés del nombre inglés "Paint Area") – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, dividida en regiones con forma aleatoria. Hace falta pintar algunas celdas de negro de tal forma que todas las celdas negras toquen una a la otra en horizontal o en vertical. Las celdas que pertenecen a la misma región deben tener igual color. No debe haber grupos de celdas de tamaño 2 x 2, formadas de celdas del mismo color. El número dentro de la celda indica qué cantidad de celdas negras hay adyacentes a esta celda en horizontal y en vertical.

Irupu (una distorsión con pronunciación japonés del nombre inglés "I-Loop") – es un pasatiempo lógico, inventado por Naoki Inaba de Japón. La tarea representa una malla de forma rectangular o cuadrada. Algunas celdas contienen círculos. Hace falta situar en la malla bloques de tamaño 1 x 3 o 3 x 1. Cada bloque contiene un círculo y toca con sus lados a dos otros bloques. Todos los bloques tocan el uno al otro formando una superficie unida.

Sashigane (traduciendo de japonés: "escuadra de carpintero") – es un pasatiempo lógico de forma rectangular o cuadrada. En algunas celdas pueden situarse círculos (con los números dentro o sin números) o flechas. Hace falta dividir la malla en regiones con forma de la letra L; ambas "patas" de tal letra región deben ser de una celda de ancho. El círculo indica el lugar donde la letra L se dobla (en la malla los círculos no están para todos los regiones). El número dentro del círculo indica la cantidad de celdas en esta región. La flecha indica el final de una "pata" de la letra L; la flecha señala al lugar donde se dobla la letra.

Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.

Chocona ("Chocolate") representa un malla rectangular o cuadrada, dividida en regiones con forma aleatoria. Hace falta pintar varias celdas de negro de tal forma que se formen zonas negras rectangulares, indiferentemente de las fronteras de las regiones. Las zonas de celdas negras pueden tocar la una a la otra sólo en diagonal. El número en la celda indica cuántas celdas puede tintarse de negro en esta región. Si una región no contiene número, cualquiera cantidad de celdas en esta región puede ser tintada de negro.

Diferentes vecinos ("Different Neighbours") – es una variedad de pasatiempo lógico. La tarea representa una malla rectangular o cuadrada, separada en regiones con forma aleatoria. Dentro de algunas regiones pueden haber números. Hace falta poner en otras regiones los números de 1 a 4 de tal forma que las regiones con los números iguales no toquen la una a la otra, incluso en diagonal.

LITS ("Nuruomino") – es un pasatiempo lógico de forma rectangular o cuadrada. La tarea representa una malla, dividida en regiones con forma aleatoria. Hace falta poner en cada región una figura de cuatro celdas (tetrominó). Las figuras pueden ser de cuatro tipos:

Un tetrominó se puede girar o reflejar de forma espejada. Las figuras del mismo tipo no deben tener lados comunes (pero pueden tocarse entre sí en diagonal). Todos los tetrominós tocan el uno al otro, formando un espacio unido. No debe haber grupos de celdas de tamaño 2 x 2, formados por completo de las celdas que pertenecen a las figuras.

Nanbaboru (una distorsión con pronunciación japonés del nombre inglés "Number Ball") – es un pasatiempo lógico de forma cuadrada, inventado por Naoki Inaba de Japón. Es necesario colocar los números de un diapasón determinado en algunas celdas de la malla de tal forma que en cada fila y cada columna cada número se use sólo una vez. Si en una celda hay un círculo, tal celda obligatoriamente debe contener un número. Si en la celda hay una cruz, en esta celda no se puede poner un número.

Tairupeinto (una distorsión con pronunciación japonés del nombre inglés "Tile Paint"; un nombre más es "Crazy Pavement") – es una variedad de pasatiempo lógico. La tarea representa una malla rectangular o cuadrada, dividida en regiones con forma aleatoria. Hace falta pintar algunas regiones de negro; una región debe contener celdas de un sólo color (blanco o negro). Los números fuera de la malla indican cuántas celdas pintadas debe haber en una fila o en una columna correspondiente.

Yin-Yang – es una variedad de pasatiempo lógico. La tarea representa una malla de forma rectangular o cuadrada, en algunas celdas de la cual pueden haber círculos blancos o negros. Hace falta colocar en todas las celdas los círculos blancos y negros de tal forma que los círculos de cada color estén relacionados los unos con los otros en horizontal o en vertical. No puede haber grupos de círculos de tamaño 2 x 2, formados con los círculos del mismo color.

Nanro es un pasatiempo lógico, que consiste en una cuadrícula de forma rectangular o cuadrada, dividida en regiones. El objetivo es colocar los números en las celdas, cumpliendo con las siguientes condiciones:

• Dentro de una región están los mismos números; son iguales a la cantidad de números en esta región.
• Una región debe contener al menos un número.
• Si dos de las celdas vecinas están separadas por la frontera de la región, no pueden contener los mismos números.
• Cualquier grupo de celdas del tamaño de 2 x 2 debe contener al menos una celda vacía.
• Todas las celdas con números forman un solo espacio, tocándose horizontal o verticalmente.

Luz y sombra ("Light and Shadow") es un tipo de pasatiempo lógico. El objetivo es dividir la cuadrícula en regiones grises y blancas. Cada región contiene exactamente un número. La región debe tener la misma cantidad de celdas que el número que contiene. Los números en las celdas blancas son parte de las regiones blancas, de la misma forma que los números en las celdas grises son parte de las regiones grises. Las regiones del mismo color no pueden compartir un borde.

Arukone ("Number Link") consiste en una cuadrícula rectangular o cuadrada con números en algunas celdas. El objetivo es conectar cada par de números con líneas continuas. Las líneas no deben cruzarse ni tocarse entre sí.

Tetroid es un pasatiempo lógico inventado por Naoki Inaba (Japón). Una cuadrícula rectangular o cuadrada contiene celdas negras. El objetivo es dividir la cuadrícula en regiones de exactamente cuatro celdas, para formar un tetromino L, I, T, S u O:

Las celdas negras no pertenecen a ningún tetromino. Los tetrominoes pueden rotarse o reflejarse. Cuando dos tetrominoes en regiones adyacentes comparten un borde, no deben ser del mismo tipo.

Sukima (del japonés "Sukimaburokku"; literalmente "espacios entre bloques") es un pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene círculos en algunas celdas. El objetivo es colocar algunas regiones que tienen el tamaño de exactamente tres celdas en la cuadrícula de tal forma que cada región contenga un círculo. Cada área de 2 x 2 debe contener al menos una celda, que no pertenece a ninguna región. Las celdas negras no pertenecen a ninguna región.

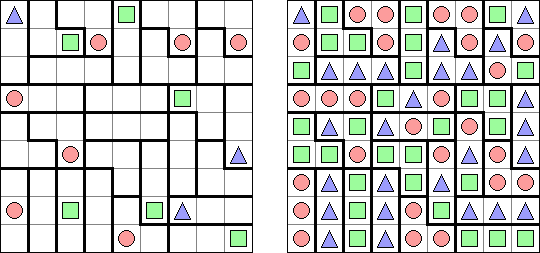
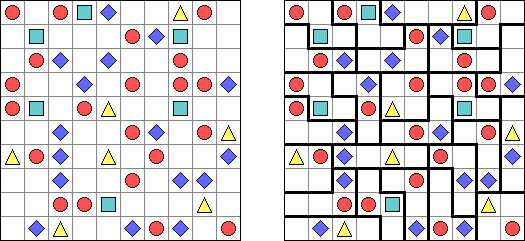
Triplets ("One or All") es un pasatiempo lógico inventado por Naoki Inaba (Japón). La tarea consiste en una cuadrícula rectangular o cuadrada dividida en regiones de exactamente tres celdas. Algunas celdas contienen figuras de 3 tipos: cuadrados, círculos y triángulos. El objetivo es completar cada celda con figuras. Cada región debe contener todas las figuras idénticas o todas las figuras diferentes. Si dos celdas vecinas están separadas por una frontera de región, las figuras en ellas deben ser diferentes.

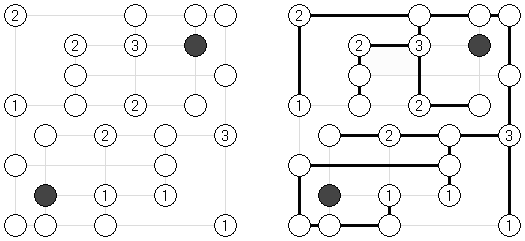
Korekutokonekuto (pronunciación japonesa de su nombre en inglés "Correct Connection") es un pasatiempo lógico creado por Naoki Inaba (Japón). La tarea consiste en círculos blancos y negros; algunos círculos blancos pueden contener números. El objetivo es conectar todos los círculos blancos por líneas horizontales y verticales (puentes). Las líneas no deben cruzar otras líneas o círculos negros. La cantidad de líneas conectadas al círculo blanco debe coincidir con el número en ese círculo.

Doppelblock es una variedad de pasatiempo lógico. Consiste en una cuadrícula cuadrada con números a la izquierda y arriba. El objetivo es ennegrecer dos celdas en cada fila y cada columna. Las celdas blancas restantes deben llenarse con los dígitos de siguiente forma:

• Cada fila y cada columna debe tener dos celdas negras.
• Las celdas blancas restantes en cada fila y cada columna se llenan con números del 1 al N-2, donde N es el tamaño del lado de la cuadrícula. Cada número debe aparecer en una fila o columna solo una vez.
• Los números fuera de la cuadrícula deben corresponder a las sumas de números en celdas ubicadas entre dos celdas negras en la fila o columna correspondiente.

Furisuri (pronunciación japonesa de su nombre en inglés "Free Three") es un pasatiempo lógico inventado por Naoki Inaba (Japón). Una cuadrícula rectangular o cuadrada contiene círculos en algunas celdas. El objetivo es ubicar regiones que tengan el tamaño de exactamente tres celdas en la cuadrícula. Cada región debe contener un círculo. Debe ser posible mover cada región por una celda en al menos una dirección en horizontal o en vertical.

Yagit (del japonés "yagi to ookami"; literalmente "cabra y lobo") es un pasatiempo lógico. El objetivo consiste en una cuadrícula rectangular o cuadrada con círculos ("cabras") y cuadrados ("lobos") en algunas celdas. Hace falta dividir la cuadrícula en regiones. Cada región debe contener o cabras o lobos (pero no ambos) y no debe estar vacía. Las líneas de frontera entre las regiones deben comenzar y terminar en los bordes de la cuadrícula. Las líneas solo pueden girar 90º en puntos negros. Las líneas pueden cruzarse entre sí, excepto en los puntos negros. No todos los puntos negros deben ser utilizados por las líneas de frontera.

Purenrupu (pronunciación japonesa de su nombre en inglés "Pure Loop") es un pasatiempo lógico creado por Naoki Inaba (Japón). Una cuadrícula rectangular o cuadrada contiene celdas negras. El objetivo es dibujar un solo bucle. El bucle ha de visitar todas las celdas blancas exactamente una vez. Los segmentos del bucle se extienden horizontal y verticalmente entre los centros de las celdas blancas.

Firumatto (pronunciación japonesa de su nombre en inglés "Fillmat") es una variedad del pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. Es necesario dividir la cuadrícula en regiones rectangulares. Cada región debe tener exactamente una celda de ancho, el otro lado de la región debe tener una longitud de 1 a 4 celdas. Una celda con un número indica el tamaño de una región. Dos regiones del mismo tamaño no deben tener borde común. Un punto de cuadrícula no debe ser compartido por las esquinas de cuatro regiones distintas.

Nawabari (traducido del japonés: "territorio") es una variedad de pasatiempo lógico. El objetivo es dividir la cuadrícula en regiones rectangulares de modo que cada región contenga exactamente un número. El número en la celda representa cuántos lados de esta celda pertenecen a las fronteras entre regiones, incluida la frontera de la cuadrícula.

Makaro es un rompecabezas lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. Cada región debe llenarse con cada uno de los dígitos del 1 al número de celdas en la región. La cuadrícula puede contener las celdas negras con flechas. La flecha apunta al número más grande entre las cuatro celdas alrededor (arriba, abajo, izquierda, derecha) de la celda negra. Cuando dos celadas son separados por la frontera de una región, los números en ellas deben ser diferentes.

Dosun-Fuwari es una variedad de pasatiempo lógico. El objetivo consiste en una cuadrícula rectangular o cuadrada dividida en regiones. La cuadrícula puede contener celdas negras que no pertenecen a ninguna región. Hace falta colocar un círculo negro y un círculo blanco en cada región de acuerdo con las siguientes reglas:

• Los círculos blancos son "globos" que son ligeros y flotan, por lo que deben colocarse en la celda superior de la cuadrícula o en la celda justo debajo de la celda negra o debajo de otro círculo blanco.
• Los círculos negros son "bolas de hierro" que son pesadas y se hunden, por lo que deben colocarse en la celda inferior de la cuadrícula o en la celda justo sobre la celda negra o sobre otro círculo negro.

Satogaeri (traducido del japonés: "volviendo a casa") es una variedad del pasatiempo lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. Algunas celdas de la cuadrícula contienen círculos (vacíos o con números dentro). El objetivo es mover los círculos vertical u horizontalmente, de modo que cada región contenga solo un círculo. Los números en los círculos indican cuántas celdas tienen que pasar. Los círculos sin números pueden moverse cualquier distancia, pero algunos de ellos permanecen fijos. Los círculos no pueden cruzar las pistas de otros círculos y no pueden moverse sobre otros círculos.

Koburin (pronunciación japonesa de su nombre en inglés "Goblin") es una variedad del pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. El objetivo es ennegrecer algunas celdas y dibujar un solo bucle continuo que no se cruza y que atraviesa correctamente todas las celdas blancas vacías. El número en la celda indica la cantidad total de celdas negras adyacentes a esta celda. La cuadrícula puede contener celdas negras no adyacentes a celdas con números. Las celdas con números no deben ennegrecerse. Dos celdas negras no deben ser adyacentes.

Sukrokuro (el nombre viene de tres pasatiempos lógicos: "Sudoku", "Kropki" y "Kakuro") combina los elementos de diferentes pasatiempos. Consiste en una cuadrícula cuadrada con celdas blancas y negras. El objetivo es completar las celdas blancas con un número en cada una, de modo que cada columna y fila contenga los números del 1 al 9 exactamente una vez. Las celdas negras contienen una barra diagonal desde la parte superior izquierda a la inferior derecha con números. El número de arriba indica la suma de números en celdas consecutivas a su derecha y el número de abajo la suma de números en celdas consecutivas de la columna hacia abajo. Si la diferencia entre dos números en las celdas vecinas es igual a 1, entonces están separadas por un punto. Si no hay un punto entre dos celdas vecinas, la diferencia entre los números en estas celdas es mayor de 1.

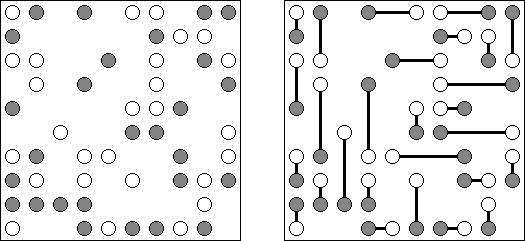
Shirokuro (traducido del japonés: "blanco/negro") es un pasatiempo lógico. Contiene círculos blancos y negros. La tarea es conectar cada círculo blanco con un círculo negro por una línea horizontal o vertical. Las líneas no pueden cruzar otras líneas. La línea entre dos círculos no puede pasar a través de otros círculos.

Roma (el nombre proviene de la frase: "todos los caminos van a Roma") es una variedad de pasatiempo lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. Algunas celdas de la cuadrícula contienen círculos negros. El objetivo es colocar flechas apuntando en una de las cuatro direcciones en cada celda vacía de tal forma que se cumplan dos condiciones:

• Cada región debe contener todas las flechas diferentes.
• Comenzando con cualquier celda, siguiendo las flechas de celda a celda, esta ruta debe terminar en la celda con el círculo negro.

Bodaburokku (pronunciación japonesa de su nombre en inglés "Border Block") es una variedad de pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas y en algunos cruces hay puntos. Es necesario dividir la cuadrícula en regiones cumpliendo con estas condiciones:

• Las celdas con el mismo número pertenecen a la misma región.
• Los puntos son los lugares donde se encuentran tres o cuatro líneas de fronteras entre regiones.
• Cada región contiene al menos una celda con un número.

Kuroshuto ("Kurochute" traducido del japonés: "disparo negro") es un pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. El objetivo es ennegrecer algunas celdas vacías. Una celda con un número indica que solo una de las celdas a esa distancia en cualquier dirección debe estar ennegrecida. Dos celdas negras no deben ser adyacentes. Todas las celdas blancas deben estar conectadas.

Toichika (traducido del japonés: "noviazgo a distancia") es un pasatiempo lógico. Consiste en una cuadrícula rectangular o cuadrada dividida en regiones. El objetivo es colocar flechas en algunas celdas de acuerdo con las siguientes reglas:

• Cada región contiene exactamente una flecha.
• Todas las flechas deben están emparejadas señalándose entre sí.
• Dos regiones con flechas emparejadas no deben ser adyacentes horizontal o verticalmente.
• Entre dos flechas emparejadas no se debe colocar ninguna otra flecha.

Usotatami es una variedad de pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. El objetivo es dividir la cuadrícula en regiones rectangulares de modo que cada región contenga exactamente un número. Cada región debe tener exactamente una celda de ancho; la longitud del otro lado NO debe ser igual al número en esta región. Un punto de cuadrícula no debe ser compartido por las esquinas de cuatro regiones.

Pipelink es un pasatiempo lógico. Consiste en una cuadrícula rectangular o cuadrada. El objetivo es dibujar un solo bucle continuo que pase por todas las celdas. El bucle debe usar todas las secciones dadas y puede cruzarse en cualquier celda.

Hakoiri (traducido del japonés: "empaquetar") es una variedad de pasatiempo lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. El objetivo es colocar exactamente un triángulo, un cuadrado y un círculo en cada región. Las mismas figuras no se pueden colocar en celdas adyacentes, ni siquiera en diagonal. Todas las figuras deben estar conectadas horizontal o verticalmente.

Nuribou (traducido del japonés: "pintar en forma de palo") es una variedad de pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. El objetivo es ennegrecer algunas celdas vacías de acuerdo con las siguientes condiciones:

• Las celdas negras dividen la cuadrícula en áreas de celdas blancas. Cada área contiene una celda con un número. Las áreas de celdas blancas no se deben tocar horizontal ni verticalmente.
• Cada área debe tener la misma cantidad de celdas blancas que el número que contiene (incluida la celda numerada).
• Las celdas negras forman franjas horizontales o verticales, que no deben ser adyacentes. Cada franja debe tener exactamente una celda de ancho.
• Si dos franjas están conectadas en diagonal, la longitud de las franjas debe ser diferente.

Tatamibari es un pasatiempo lógico. Una cuadrícula rectangular o cuadrada contiene 3 tipos de símbolos: cruz, barra horizontal, barra vertical. El objetivo es dividir la cuadrícula en regiones rectangulares cumpliendo con las siguientes condiciones:

• Cada región debe contener una celda con un símbolo.
• Una región con una cruz debe ser cuadrada.
• Si una región contiene una barra horizontal, el ancho de la región debe ser mayor que su altura.
• Si una región contiene una barra vertical, el ancho de la región debe ser menor que su altura.
• Un punto de cuadrícula no debe ser compartido por las esquinas de cuatro regiones.

Sol y Luna ("Sun and Moon"; "Munraito" pronunciación japonesa de su nombre en inglés "Moonlight") es un pasatiempo lógico. Una cuadrícula cuadrada contiene planetas en algunas celdas. El objetivo es colocar exactamente una estrella y una nube de polvo de estrellas (en forma de un cuadrado de color oscuro) en cada fila y cada columna de la cuadrícula. Si se ilumina un semicírculo particular de un planeta, debe haber una estrella en ese rango para iluminarlo. Una estrella brilla solo horizontal y verticalmente. Los planetas y las nubes de polvo de estrellas bloquean la luz de las estrellas.

Kojun (traducido del japonés: "subordinación de menores a mayores") es un pasatiempo lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. Algunas celdas contienen números. Cada región debe llenarse con cada uno de los dígitos del 1 al número de celdas en la región. Cuando dos números son adyacentes, los números deben ser diferentes. El número superior de dos números adyacentes verticalmente en la misma región debe ser mayor que el número inferior.

Usowan (traducido del japonés: "un mentiroso") es un pasatiempo lógico. Una cuadrícula se divide en regiones rectangulares y cuadradas. Algunas de las celdas de la cuadrícula están numeradas. El objetivo es ennegrecer algunas celdas de la cuadrícula de acuerdo con las siguientes reglas:

• Las celdas con números son siempre blancas.
• Un número en una celda indica cuántas celdas negras deben colocarse adyacentes a sus cuatro lados. Sin embargo, en cada región hay un número (y solo uno) incorrecto (muestra una cantidad incorrecta de celdas negras).
• Dos celdas negras no deben ser adyacentes.
• Todas las celdas blancas deben estar conectadas.

Gokigen Naname (traducido del japonés: "estar de mal humor", "a tuerto y a derecho"; otros nombres "Slalom", "Slant") es una cuadrícula rectangular o cuadrada. Los círculos con números del 0 al 4 pueden estar situados en intersecciones de líneas dentro de la cuadrícula. El objetivo es completar una línea diagonal en cada celda. El número en cada círculo es igual al número de líneas que se extienden desde ese círculo. Las líneas diagonales no deben formar un bucle cerrado.

Hebi-Ichigo (traducido del japonés: "serpiente en los matorrales de fresas") es una variedad de pasatiempo lógico. Consiste en una cuadrícula cuadrada o rectangular, algunas celdas de la cual están ennegrecidas. El objetivo es insertar a las celdas los números del 1 al 5 de acuerdo con las siguientes condiciones:

• Los números forman una cadena secuencial de cinco celdas desde 1 ("cabeza") a 5 ("cola") conectadas horizontal y verticalmente (formando "serpiente").
• Las serpientes no pueden tocar a otras serpientes horizontal o verticalmente, pero se permite que se toquen diagonalmente.
• No se permite que las serpientes aparezcan frente a la cabeza de otra serpiente. Los ojos de la serpiente están ubicados en un lado de la cabeza (celda con el número 1), opuesto al lado al que está conectado su cuerpo (celda con el número 2). Una serpiente mira en la dirección de sus ojos hasta que se alcanza una celda negra o el borde de la cuadrícula.
• El número en la celda negra muestra el valor del número más cercano en la dirección de la flecha. Este número debe aparecer antes que cualquier otra celda negra. Una celda negra con un cero significa que no hay serpiente en la dirección de la flecha hasta la siguiente celda negra o el borde de la cuadrícula.

Hamle (traducido del turco: "movimiento") es un pasatiempo lógico que consiste en una cuadrícula rectangular o cuadrada algunas de las celdas de la cual están ennegrecidas y tienen números. El objetivo es mover cada celda negra con número en una de las cuatro direcciones, de modo que los números en las celdas indiquen la longitud de sus movimientos. Cuando se realizan todos los movimientos, todas las celdas blancas deben estar conectadas horizontal o verticalmente y las celdas con número no deben compartir un borde.

Gyokuseki ("Gyokusekikonko Puresu"; traducido del japonés: "piedras preciosas u ordinarias") es un pasatiempo lógico de forma cuadrada. El objetivo es llenar la cuadrícula con círculos negros ("gemas") y círculos blancos ("piedras"). Cada fila y cada columna contiene un círculo negro y una cantidad aleatoria de círculos blancos. El número fuera de la cuadrícula indica cuántos círculos se pueden ver en la fila o columna correspondiente hasta e incluyendo el círculo negro.

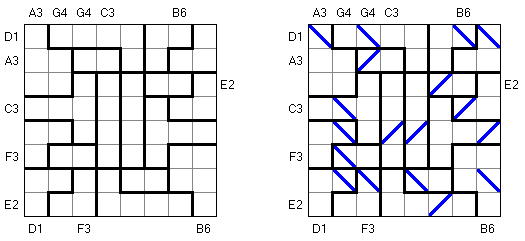
Kin-Kon-Kan es una variedad de pasatiempo lógico que consiste en una cuadrícula rectangular o cuadrada dividida en regiones. El objetivo es completar algunas celdas con líneas diagonales ("espejos"). Cada región contiene exactamente un espejo. Los pares de letras y números en los bordes de la cuadrícula se pueden conectar mediante líneas rectas ("rayos láser") que rebotan del mismo número de espejos que el número en el par de letras y números. Cada espejo debe reflejar al menos un rayo láser.

Ichimaga consiste de círculos con números. El objetivo es conectar todos los círculos por líneas horizontales y verticales. La cantidad de líneas conectadas al círculo debe coincidir con el número en ese círculo. Se puede conectar cualquier cantidad de líneas al círculo vacío (pero al menos uno). Las líneas no deben cruzar otras líneas. La línea puede cambiar de dirección 90 grados no más de una vez.

Shimaguni (traducido del japonés: "país insular") es un pasatiempo lógico. Una cuadrícula rectangular o cuadrada se divide en regiones. El objetivo es ennegrecer algunas celdas de una cuadrícula de acuerdo con las siguientes reglas:

• Todas las celdas negras en una región deben estar conectadas horizontal y verticalmente.
• Una celda con un número indica cuántas celdas en la región deben ennegrecerse.
• En regiones sin número, cualquier cantidad de celdas puede ennegrecerse (al menos una).
• Dos regiones con la misma cantidad de celdas negras no deben ser adyacentes.
• Cuando dos celdas son adyacentes a través de un límite de región, al menos una celda debe ser blanca.

Meadows es un pasatiempo lógico que consiste en una cuadrícula rectangular o cuadrada. Algunas de las celdas tienen círculos (“vacas”) en ellas. El objetivo es dividir la cuadrícula en bloques cuadrados de modo que cada bloque contenga exactamente un círculo.

Yajisan-Kazusan (traducido del japonés: "flecha – número") es una variedad de pasatiempo lógico. Consiste es una cuadrícula cuadrada o rectangular, en algunas celdas de la cual hay números con flechas. El objetivo es ennegrecer algunas celdas de acuerdo con las siguientes condiciones:

• Las celdas negras no deben estar conectadas horizontal o verticalmente.
• Una celda con un número puede ennegrecerse.
• Todas las celdas blancas deben estar conectadas horizontal o verticalmente.
• Una celda que contiene un número y una flecha representa cuántas celdas negras hay en la fila o columna señalada por la flecha.
• No todas las celdas con números y flechas contienen información verdadera. Las celdas con números deben ennegrecerse si contienen pistas falsas, pero las celdas numeradas pintadas de negro no necesariamente contienen pistas falsas. Cuando el pasatiempo sea resuelto, los números y las flechas en las celdas blancas deben contener información verdadera, y los números y las flechas en las celdas negras deben ignorarse.

Snake Pit es un pasatiempo lógico de forma cuadrada o rectangular. El objetivo es dividir la cuadrícula en regiones ("serpientes") de acuerdo con las siguientes reglas:

• Una serpiente es un camino de una celda de ancho y al menos dos celdas de largo. Una serpiente no puede tocarse a sí misma, ni siquiera en diagonal.
• Una celda con un círculo debe estar en uno de los extremos de una serpiente. Una serpiente puede contener una celda con un círculo, dos celdas con un círculo o ninguna celda con un círculo.
• Una celda con un número debe ser parte de una serpiente con una longitud de exactamente ese número de celdas. Una serpiente puede contener cualquier cantidad de celdas con números.
• Dos serpientes de la misma longitud no deben ser adyacentes horizontal o verticalmente.
• Una celda con una cruz 'X' no puede ser el final de una serpiente.

Hiroimono ("Goishi Hiroi"; traducido del japonés: "cosas recogidas") es una variedad de pasatiempo lógico cuyas reglas se inspiraron en el juego japonés de Go. La cuadrícula contiene círculos ("piedras") colocados en algunos puntos de la cuadrícula. El objetivo es moverse a lo largo de las líneas de la cuadrícula y recoger todas las piedras (numerarlas en el orden en que las recoge) de acuerdo con las siguientes reglas:

• Comience en cualquier piedra.
• Cuando se encuentra una piedra, se recoge.
• Cuando se levanta una piedra, se puede cambiar la dirección.
• No está permitido invertir la dirección.

Diversión acuática ("Water Fun") se juega en una cuadrícula rectangular o cuadrada. El objetivo es llenar de agua algunas partes de la cuadrícula. Los números fuera de la cuadrícula muestran cuántas celdas de cada fila y columna deben llenarse con agua. Las áreas conectadas de celdas rellenas deben tener el mismo nivel de agua en todas partes, como en una serie de tuberías.

Ida y vuelta ("Round Trip") es una especie de rompecabezas lógico. El objetivo es dibujar un solo bucle en una cuadrícula rectangular o cuadrada. El bucle puede entrecruzarse de forma ortogonal, pero en otras circunstancias no puede ni tocar ni cruzar a sí mismo. Los números a lo largo de los bordes de la cuadrícula indican el número de celdas ocupadas por la sección correspondiente del bucle en dicha fila o columna.

Cruzar números ("Number Cross") consiste en una cuadrícula cuadrada con números. El objetivo es ennegrecer algunas celdas. Los números fuera de la cuadrícula muestran las sumas de los números en celdas blancas en la fila o columna correspondiente.

Santoitchi (del japonés, literalmente "tres y uno") es un rompecabezas lógico inventado por Naoki Inaba (Japón). Una cuadrícula rectangular o cuadrada contiene números en algunas celdas. La tarea es ennegrecer algunas celdas vacías de acuerdo con las reglas: Todas las celdas blancas deben dividirse en regiones que tengan el tamaño de exactamente tres celdas. Dos celdas negras no pueden ser adyacentes ortogonalmente. Cada región debe contener un número. El número indica cuántas celdas negras comparten un borde con esa región.

Hamusando (una distorsión con pronunciación japonés del nombre inglés Tostadas de jamón – "Ham Sandwich") es un rompecabezas lógico inventado por Naoki Inaba (Japón). El objetivo es llenar una cuadrícula con cuadrados (“tostadas”) y círculos (“trozos de jamón”). Cada fila y cada columna contiene dos cuadrados y N círculos (N se da para cada rompecabezas). El número en el borde de la cuadrícula indica cuántos círculos deben colocarse entre los dos cuadrados en la fila o columna correspondiente.

Sigue los números ("Trace Numbers") consiste en una cuadrícula rectangular o cuadrada con números en algunas celdas. El objetivo es dibujar tantas líneas en la cuadrícula como celdas que tengan el número 1. La línea solo puede viajar horizontal o verticalmente, y nunca en diagonal. La línea comienza en la celda con el número 1 y visita todas las celdas con números en orden hasta el número más alto. Cada celda debe ser visitada exactamente una vez; las líneas no pueden cruzarse.

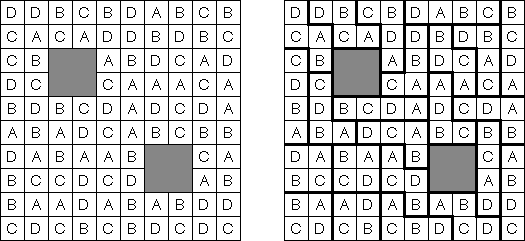
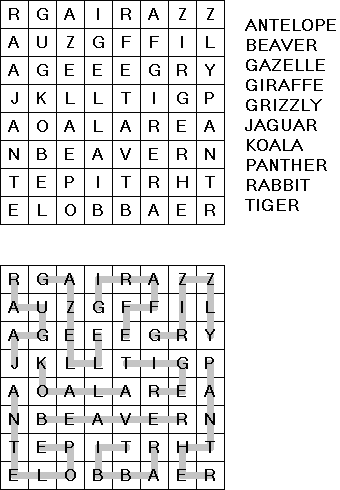
Dividir en áreas ("Area Division") se juega en una cuadrícula llena de letras latinas. El objetivo es dividir la cuadrícula en regiones. Cada región debe tener todas las letras del rango dado. Cada región ha de contener cada letra exactamente una vez. Cada letra debe ser parte de exactamente una región.

Sukoro consiste en una cuadrícula rectangular o cuadrada con números del 1 al 4 en algunas celdas. El número dentro de una celda representa cuántas celdas vecinas contienen números. Cuando dos celdas con números son ortogonalmente adyacentes, los números deben ser diferentes. Todas las celdas con números deben estar conectadas horizontal o verticalmente.

Entrada/Salida ("EntryExit") consiste en una cuadrícula rectangular o cuadrada dividida en regiones. El objetivo es dibujar un único bucle continuo que no se cruce y que pase por todas las celdas. Puede entrar y salir de cada región sólo una vez.

Emplazar números ("Sign In") se juega en una cuadrícula cuadrada. El objetivo es completar cada celda con números desde 1 al N, donde N es el tamaño de cada lado del rompecabezas. Ningún número puede aparecer dos veces en una fila o columna. Algunos dígitos pueden estar emplazados desde el principio. Si la diferencia absoluta entre dos dígitos en celdas vecinas es igual a 1, entonces están separados por un signo “+” o “-”. Si el borde entre celdas contiene signo “+”, el dígito en una celda a la izquierda o arriba es en uno más bajo que el dígito en una celda a la derecha o abajo. Si el borde entre celdas contiene signo “-”, el dígito en una celda a la izquierda o arriba es en uno más grande que el dígito en una celda a la derecha o abajo. Todas las instancias de dígitos consecutivos se muestran con estos signos.

Kuroshiro ("Kuroshirorupu"; del japonés, literalmente "bucle en blanco y negro") se juega en una cuadrícula con círculos en blanco y negro en algunas celdas. El objetivo es dibujar un solo bucle continuo que no se cruce y que pase correctamente por todas las celdas con un círculo. El bucle no debe girar entre dos círculos sucesivos del mismo color. Entre dos círculos sucesivos de diferentes colores, el bucle debe girar exactamente una vez.

Moonsun (del nombre inglés Luna o Sol – "Moon or Sun") es un rompecabezas lógico inventado por Nikoli. Una cuadrícula rectangular o cuadrada está dividida en regiones. La cuadrícula contiene círculos blancos y negros en algunas celdas. El objetivo es dibujar un solo bucle que no se cruce. El bucle debe cruzar los bordes de cada región exactamente dos veces. En una región el bucle debe visitar todas las celdas con círculos negros o todas las celdas con círculos blancos. Las regiones con círculos negros visitados deben alternarse con regiones donde se visitaron círculos blancos.

Rectslider (del nombre inglés "Rectangle-Slider", también conocido como "Shikaku suraida") consiste en una cuadrícula rectangular o cuadrada con celdas negras. La tarea es mover las celdas negras vertical u horizontalmente, de modo que las celdas negras formen rectángulos que tengan un área mayor que una celda. Dos rectángulos negros no deben ser adyacentes ortogonalmente. Los números en las celdas negras indican por cuántas celdas tienen que pasar. Las celdas negras sin números pueden moverse cualquier distancia, pero algunas de ellas se quedan sin moverse. Las celdas negras no pueden cruzar rastros de otras celdas negras y no pueden moverse sobre otras celdas negras.

Stostone (del nombre inglés "Sto-Stone", Piedra sobre piedra – "Stone on Stone") es un rompecabezas lógico inventado por Nikoli. Una cuadrícula rectangular o cuadrada está dividida en regiones. El objetivo es ennegrecer algunas celdas de la cuadrícula ("piedras") de acuerdo con las siguientes reglas:

• Todas las celdas negras en una región deben estar conectadas horizontal o verticalmente.
• La celda con un número indica cuántas celdas de la región deben ennegrecerse.
• En las regiones sin número se puede ennegrecer cualquier cantidad de celdas (al menos una).
• Cuando dos celdas son adyacentes ortogonalmente a través de un límite de región, al menos una celda debe ser blanca.
• Si todas las piedras "caen abajo", deben cubrir exactamente la mitad inferior de la cuadrícula.

Kohi Gyunyu (del japonés, literalmente "leche de café") consiste en círculos blancos, negros y grises. El objetivo es conectar círculos mediante líneas horizontales y verticales. Todos los círculos conectados forman un grupo. Cada grupo debe contener exactamente un círculo gris y cantidades iguales de círculos blancos y negros. Las líneas no deben cruzarse con otras líneas. Los círculos blancos y negros no pueden ser conectados directamente.

Mirukuti (una distorsión con pronunciación japonés del nombre inglés "Milk Tea", Té con leche o "Milk-T") consiste en una cuadrícula rectangular o cuadrada con círculos blancos y negros en algunas celdas. El objetivo es conectar cada grupo de tres círculos (uno negro y dos blancos) mediante una línea en forma de T. Dos círculos blancos deben estar conectados por un segmento de línea recta de la línea en forma de T. Las líneas no deben cruzarse con otras líneas.

Slash Pack es un rompecabezas lógico inventado por Yosuke Imai (Japón). La cuadrícula de forma irregular contiene números desde 1 a N en algunas celdas. El objetivo es dividir la cuadrícula en regiones colocando líneas diagonales en celdas vacías. Cada región debe contener los números desde 1 a N exactamente una vez. Dos diagonales no pueden cruzarse en una celda, y no puede haber finales de línea sueltos, es decir diagonales con final que no toque otra línea o borde de la cuadrícula.

Nurimaze ("Nurimeizu"; del japonés, literalmente "pintar el laberinto") es un rompecabezas lógico. Consiste en una cuadrícula rectangular o cuadrada dividida en regiones. El objetivo es ennegrecer algunas regiones de acuerdo con las siguientes reglas:

• Las celdas con letras, círculos o triángulos siempre son blancas.
• Las celdas blancas forman un camino desde la celda con S (“start”) hasta la celda con G ("goal"); este camino ha de tener exactamente una celda de ancho.
• Ningún área de celdas de tamaño 2 x 2 dentro de la cuadrícula puede tener el mismo color.
• Todas las celdas blancas deben formar un área ortogonalmente continua.
• El camino desde S hasta G ha de incluir todas las celdas con círculos y ninguna celda con triángulo.
• Las celdas blancas no deben formar un bucle.

Vista al Canal ("Canal View") se juega en una cuadrícula rectangular. Algunas de sus celdas tienen números en ellas. El objetivo es ennegrecer algunas celdas de la cuadrícula de acuerdo con las siguientes reglas:

• Todas las celdas negras deben crear un solo grupo conectado.
• Ningún área de celdas de tamaño 2 x 2 dentro de la cuadrícula puede contener todas las celdas negras.
• Las celdas numeradas no deben ser negras.
• Cada celda numerada indica la cantidad total de celdas negras conectadas vertical y horizontalmente a esa celda numerada, en línea recta hasta la siguiente celda blanca o el borde de la cuadrícula.

Camino rural ("Country Road") es un rompecabezas lógico inventado por Nikoli. El rompecabezas consiste en una cuadrícula rectangular de cualquier tamaño dividida en regiones. El objetivo es dibujar un solo bucle continuo que no se cruce y que conecte los centros de las celdas de la cuadrícula. El bucle debe visitar cada región exactamente una vez. El número en una región indica cuántas celdas de esta región son visitadas por el bucle. En regiones sin número, el bucle puede visitar cualquier número de celdas. Si el bucle no visita dos celdas vecinas, estas celdas deben estar en la misma región.

Nondango (el dango es un plato japonés, pequeñas bolas hechas de harina de arroz y ensartadas en palitos de bambú) es un rompecabezas lógico publicado por Nikoli. Una cuadrícula rectangular o cuadrada es dividida en regiones. Cada región contiene círculos en algunas celdas. El objetivo es ennegrecer algunos círculos de acuerdo con las siguientes reglas:

• Cada región ha de contener un círculo negro.
• Tres círculos consecutivos del mismo color nunca deben aparecen en ninguna fila, columna o diagonal (hebe haber un círculo de otro color o una celda vacía entre ellos).

Mintonette (el nombre original del juego conocido como voleibol) se juega en una cuadrícula de forma irregular con círculos en algunas celdas. El objetivo es conectar círculos en parejas, dibujando una línea que pase horizontal y verticalmente por los centros de estas celdas. Las líneas no pueden tocarse o cruzarse entre sí. Si un círculo contiene un número, este representa la cantidad de giros que de la línea entre los dos círculos. Si los dos círculos no tienen número, la línea puede dar cualquier cantidad de giros entre ellos. Todas las celdas deben ser utilizadas por las líneas, y cada círculo debe estar conectado a otro círculo.

Laberinto de flechas ("Arrow Maze") es un rompecabezas lógico con números y flechas. Consiste en una cuadrícula rectangular o cuadrada con flechas. El objetivo es encontrar un camino a través de la cuadrícula visitando cada celda sólo una vez y marcándolo con números consecutivos. El camino comienza desde la celda con el número 1. El camino puede saltar de una celda a otra en dirección horizontal, vertical o diagonal, pero sólo en la dirección de la flecha. Algunos de los números vienen ya marcados.

Telaraña de flechas ("Arrow Web") es un rompecabezas lógico. Una cuadrícula rectangular o cuadrada está llena de flechas. El objetivo es ennegrecer algunas de las flechas para que cada flecha en la cuadrícula apunte exactamente a una flecha negra.

Hanare ("Hanaregumi"; del japonés, literalmente "pareja familiar") es un rompecabezas lógico. Una cuadrícula cuadrada o rectangular es dividida en regiones. El objetivo es colocar un número en cada región. El número es igual al tamaño de la región. La distancia entre dos números vecinos horizontal o verticalmente debe ser igual a la diferencia entre estos números.

Oasis ("Oases") es un rompecabezas lógico. Una cuadrícula rectangular o cuadrada contiene círculos con números en algunas celdas. El objetivo es ennegrecer algunas celdas de acuerdo con las siguientes reglas:

• Las celdas ennegrecidas no deben compartir un borde.
• Las celdas con círculos no pueden ser ennegrecidas.
• Las celdas sin sombrear deben conectarse horizontal o verticalmente.
• Las celdas sin sombrear no deben cubrir un área de tamaño 2 x 2.
• Cada número dentro de un círculo representa la cantidad de otros círculos a los que se puede llegar desde ese círculo pasando sólo por celdas vacías (sin sombrear y sin círculo). Un círculo al que se puede llegar por más de un camino sigue contando como sólo un círculo para propósitos de determinar el número.

Conejos y Árboles ("Rabbits and Trees"; "Raitonanba" es una distorsión con pronunciación japonés del nombre inglés "Light Number") es una cuadrícula cuadrada con números en algunas celdas. La tarea es colocar exactamente un círculo blanco (“conejo”) y un círculo negro (“árbol”) en cada fila y cada columna. El número indica cuántos círculos blancos (“conejos”) se pueden ver en la fila y columna correspondientes. Un conejo es visible solo cuando no está escondido detrás de un árbol.

Flechas y Estrellas ("Stars and Arrows") consiste en una cuadrícula rectangular o cuadrada con flechas en algunas celdas. El objetivo es colocar estrellas en celdas vacías. Cada flecha apunta exactamente a una estrella y cada estrella cuenta sólo para una flecha. Los números fuera de la cuadrícula muestran el número de estrellas en la fila o columna correspondiente.

Kanjo ("Kanjo-sen supesharu"; del japonés, literalmente "línea de anillo especial") es un rompecabezas lógico. Una cuadrícula rectangular o cuadrada contiene círculos con números en algunas celdas. El objetivo es dibujar bucles que pasen correctamente por todas las celdas. Un bucle puede cruzar a sí mismo o a otros bucles. Todos los fragmentos de línea ya marcados deben ser usadas como parte de un bucle. Las celdas con el mismo número pertenecen al mismo bucle. Las celdas con diferentes números pertenecen a diferentes bucles. Un bucle debe pasar por al menos una celda con un número (en la cuadrícula hay exactamente tantos bucles como números diferentes en ella). Una celda con un número no debe contener el punto de intersección donde un bucle se cruza consigo mismo o con otro bucle.

Rukkuea (una distorsión con pronunciación japonés del nombre inglés "Look-Air") es un rompecabezas lógico inventado por Nikoli. El rompecabezas consiste en una cuadrícula rectangular o cuadrada con números en algunas celdas. Es necesario ennegrecer algunas celdas de acuerdo con las siguientes reglas:

• Celdas negras forman un área de forma cuadrada.
• No debe haber áreas negras que se toquen entre sí horizontal o verticalmente (sólo en diagonal).
• Áreas negras del mismo tamaño no deben "verse" entre sí: las líneas horizontales o verticales entre dos áreas negras deben contener al menos un área negra de otro tamaño.
• Cada número muestra cuántas de las cinco celdas (la que tiene el número más las cuatro celdas vecinas ortogonalmente) deben ennegrecerse.

Golem Grad (una isla en el lago Prespa, en la República de Macedonia del Norte) combina las reglas de los rompecabezas Nurikabe y Serpiente. Una cuadrícula rectangular o cuadrada contiene círculos y números en algunas celdas. El objetivo es ennegrecer algunas celdas de acuerdo con las siguientes reglas. Las celdas negras dividen la cuadrícula en áreas de celdas blancas (“islas”), cada una de las cuales contiene como máximo un número. La isla con un número debe tener la misma cantidad de celdas blancas que indica este número. Dos islas no pueden estar conectadas, es decir sólo pueden tocarse en diagonal. Todas las celdas negras deben formar un área ortogonalmente continua. Ningún área de celdas de tamaño 2 x 2 dentro de la cuadrícula puede tener el color negro. Todas las celdas negras deben ser divisibles en “serpientes” con cabezas y colas marcadas como círculos en la cuadrícula. Serpientes no deben cruzarse entre sí.

Trilogía ("Trilogy") consiste en una cuadrícula cuadrada o rectangular con figuras en algunas celdas: cuadrados, círculos y triángulos. El objetivo es llenar cada celda con figuras. Tres figuras consecutivas no deben ser todas iguales y no deben ser todas diferentes en ninguna fila, columna o diagonal.

Grades es un rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular con números fuera de ella. El objetivo es ordenar los números en la cuadrícula, cumpliendo con las siguientes reglas:

• Las celdas con números no deben tocarse horizontal, vertical o diagonalmente.
• El número a la izquierda o en la parte superior de la cuadrícula muestra cuántos números hay en esa fila o columna.
• El número a la derecha o debajo indica la suma de los números en esa fila o columna.

Hukuwall (del japonés: “la forma secreta de construir un muro”) es un rompecabezas de lógica inventado por Nishiyama Yukari de Japón. En una cuadrícula cuadrada o rectangular, algunas celdas contienen letras. El objetivo es llenar las celdas vacías con líneas que salen de las letras. Cada letra debe corresponder a un número: las mismas letras - los mismos números, diferentes letras - diferentes números. El número debe ser igual a la longitud total de las líneas que salen de la celda con la letra. Una línea no puede pasar por encima de una celda con letra. Las líneas no deben cruzarse. Si la cuadrícula contiene varias letras idénticas, entonces para cada letra la cantidad de direcciones de líneas ha de ser diferente.

Nurimisaki (del japonés: “colorear el cabo”) es un rompecabezas de lógica. En una cuadrícula cuadrada o rectangular, algunas celdas contienen círculos (con números o vacíos). El objetivo es pintar algunas de las celdas de negro, cumpliendo con las siguientes reglas:

• Las celdas sin pintar deben formar un camino de una celda de ancho.
• La celda con el círculo ha de quedar en blanco.
• La celda con el círculo debe tener exactamente una celda blanca adyacente horizontal o verticalmente. Las celdas adyacentes restantes deben ser negras.
• La celda blanca sin círculo debe tener al menos dos celdas blancas adyacentes horizontal y verticalmente.
• El número en el círculo muestra cuántas celdas blancas son visibles horizontal y verticalmente (incluida la celda con el círculo). La “mirada” se extiende hasta la celda negra o hasta el borde de la cuadrícula.
• Todas las celdas blancas deben tocarse entre sí horizontal o verticalmente.
• No debe haber un área de 2 x 2 que consta de celdas del mismo color.

Starry Night ("Niapuresu", "Near Place") es una variedad de rompecabezas de lógica. El objetivo es colocar en una cuadrícula cuadrada una estrella, un círculo blanco (“sol”) y un círculo negro (“luna”) en cada fila y cada columna de tal forma que las figuras idénticas no se toquen en diagonal. Las figuras fuera de la cuadrícula indican la distancia entre la estrella y la figura más cercana en la fila o columna correspondiente:

• Si hay un círculo blanco fuera de la cuadrícula, el círculo blanco debe estar más cerca a la estrella que el círculo negro.
• Si hay un círculo negro fuera de la cuadrícula, el círculo negro debe estar más cerca de la estrella que el círculo blanco.
• Si hay una estrella fuera de la cuadrícula, entonces los círculos blanco y negro deben estar ubicados a la misma distancia de la estrella.

Douieru (del japonés: “iguales y diferentes”) es un rompecabezas de lógica inventado por Nishiyama Yukari de Japón. Una cuadrícula cuadrada o rectangular contiene círculos en algunas celdas. El objetivo es dividir la cuadrícula en regiones con la forma de la letra latina L; ambas “patas” de la región deben tener una celda de ancho. El círculo indica dónde se dobla la L (hay círculos para todas las regiones de la cuadrícula). El doble círculo indica que ambas “patas” deben tener la misma longitud. El círculo negro indica que las “patas” de la región deben tener diferentes longitudes. El círculo blanco indica que no se sabe nada sobre la longitud de las “patas”.

Tetoron es un rompecabezas de lógica creado por Nishiyama Yukari de Japón. Una cuadrícula cuadrada o rectangular contiene diferentes símbolos en algunas celdas. El objetivo es dividir la cuadrícula en regiones de cuatro celdas (tetrominós). Cada región debe contener dos símbolos diferentes. Las regiones que tienen la misma forma deben contener los mismos pares de símbolos (los tetrominós se pueden rotar o reflejar).

Sashikaku (del japonés: “área como diferencia”) es un rompecabezas de lógica con forma cuadrada o rectangular. Algunas celdas de la cuadrícula contienen números. El objetivo es dividir la cuadrícula en regiones rectangulares y cuadradas de tal forma que cada región contenga solo un número, igual a la diferencia entre el ancho y el alto de la región.

Heki es un rompecabezas de lógica inventado por Nishiyama Yukari de Japón. Algunas celdas de la cuadrícula cuadrada o rectangular contienen números. El objetivo es dividir esta cuadrícula en regiones de seis celdas. Cada región debe contener dos números. El número muestra cuántas celdas de la región están adyacentes a la celda con el número horizontal y verticalmente.

Castle Wall es un rompecabezas de lógica inventado por Palmer Mebane de EE.UU. En una cuadrícula cuadrada o rectangular, algunas de las celdas están bordadas, la otra parte de las celdas está pintada de negro; algunas de estas celdas contienen números y flechas. El objetivo es trazar una línea cerrada, cumpliendo con las siguientes reglas:

• La línea no debe pasar a través de celdas negras ni por celdas bordadas. No es necesario que pase por todas las celdas vacías.
• La línea no debe entrecruzarse.
• Las celdas negras deben estar fuera de la línea cerrada; las celdas bordadas deben ubicarse dentro de la línea. Las celdas grises pueden ubicar tanto dentro como fuera de la línea cerrada.
• El número indica la cantidad de segmentos de línea en la dirección en la que apunta la flecha. (En otras palabras, el número es igual a la cantidad de bordes de celdas que la línea cruza en esa dirección.)

Deddoanguru (pronunciación japonesa del nombre en inglés “Dead Angle”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Una cuadrícula cuadrada o rectangular contiene círculos con números en algunas celdas. El objetivo es dividir la cuadrícula en regiones de forma aleatoria para que cada región contenga un círculo. El círculo es un “ojo” cuya mirada se extiende horizontal y verticalmente hasta el borde de la región. El número en el círculo corresponde a la cantidad de celdas de la región que no son visibles desde el círculo.

Endorain (pronunciación japonesa de la expresión inglesa “End Line”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Consiste en una cuadrícula cuadrada o rectangular, dividida en regiones de forma aleatoria. En algunas regiones puede haber números. El objetivo es dibujar líneas rectas horizontales o verticales que conecten los centros de dos celdas en diferentes regiones. El número corresponde a la cantidad de extremos de línea en esa región. Sólo se debe trazar una línea a través de cada celda.

Nuraf ("Araf Nurikabe") es una combinación de reglas de rompecabezas Nurikabe y Araf. En una cuadrícula cuadrada o rectangular, algunas celdas contienen números. El objetivo es pintar algunas celdas de negro, cumpliendo las siguientes reglas:

• Todas las celdas negras deben estar conectadas entre sí.
• No se debe pintar la celda con el número.
• Las celdas blancas forman “islas” de forma aleatoria. Dos islas cualesquiera pueden tocarse solo con sus esquinas.
• No debe haber un solo cuadrado de 2 x 2 en la cuadrícula que esté formado únicamente por celdas negras.
• Cada isla contiene dos números. El área de la isla debe ser igual al valor intermedio entre estos dos números. Por ejemplo, si una isla contiene los números 2 y 5, su área debe ser igual a tres o cuatro celdas.

Miti (del japonés, “camino”) es un rompecabezas de lógica inventado por Nishiyama Yukari de Japón. Dentro de una cuadrícula cuadrada o rectangular, hay puntos en las intersecciones de las líneas. El objetivo es pintar los bordes entre las celdas con color negro para obtener un camino cerrado de una celda de ancho. El camino debe pasar por todas las celdas, sin callejones sin salida. Los puntos indican las intersecciones de tres bordes de celdas (todos esos puntos están marcados en la cuadrícula).

Arofuro (pronunciación japonesa de la expresión inglesa “Arrow Flow”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Consta de una cuadrícula cuadrada o rectangular con números en algunas celdas. El objetivo es colocar flechas en todas las celdas libres, cumpliendo con las siguientes reglas:

• La flecha apunta en una de las cuatro direcciones (derecha, izquierda, arriba, abajo).
• Las flechas que apuntan en la misma dirección no deben colocarse en celdas adyacentes.
• Desde cualquier celda con una flecha se puede seguir una ruta a una celda con un número, si ir de una celda a otra en la dirección de las flechas.
• El número en una celda indica el total de flechas que se usan para llegar a esa celda.

Every Second Turn (“Alternate Corners”, “Every Second Breakpoint”) es una variación de rompecabezas lógico. Una cuadrícula cuadrada o rectangular contiene círculos en algunas celdas. El objetivo es trazar una línea cerrada a través de todas las celdas de la cuadrícula. La línea no debe entrecruzarse. Cuando la línea cruza un círculo, debe girar 90 grados. En cada sección entre dos círculos la línea debe girar exactamente una vez.

Mobiriti (pronunciación japonesa de la expresión inglesa “Mobility”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Consta de una cuadrícula cuadrada o rectangular, en algunas celdas de la cual hay círculos con números. El objetivo es pintar algunas celdas de negro. Las celdas con círculos no se pueden pintar. El número en el círculo corresponde al número de celdas blancas vacías que se pueden alcanzar moviéndose horizontal y verticalmente.

Mubunanba (pronunciación japonesa de la expresión inglesa “Move Number”) es un rompecabezas lógico inventado por Naoki Inaba de Japón. Consta de una cuadrícula cuadrada o rectangular con números en algunas celdas. El objetivo es colocar bloques de tres celdas en la cuadrícula. No todas las celdas deben estar ocupadas por bloques. Cada bloque ha de tener una celda con un número. El número indica la cantidad de direcciones disponibles para mover el bloque horizontal y verticalmente.

Terra X consta de una cuadrícula cuadrada o rectangular dividida en regiones. Algunas regiones pueden tener números dentro. El objetivo es poner los números del 0 al 9 en las regiones restantes de modo que las regiones con los mismos números no sean vecinas (las regiones pueden tocarse entre sí en diagonal). En aquellos puntos donde se tocan cuatro regiones, la suma de los números en estas regiones debe ser igual a 10. (Para facilitar la solución, todos esos puntos están marcados con pequeños círculos negros).

Rimotoejji (pronunciación japonesa de la expresión inglesa “Remote Edge”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. El objetivo es trazar una línea cerrada a través de todos los puntos de la cuadrícula cuadrada o rectangular. La línea no debe entrecruzarse. La cuadrícula contiene flechas y cruces: todas las figuras deben estar dentro de la línea cerrada. Las figuras determinan qué secuencias de celdas proceden de la celda con la figura y se extienden hasta el límite visible de la línea horizontal y verticalmente. La flecha apunta hacia la secuencia más larga de celdas. La cruz se sitúa en la celda de la que salen dos o más secuencias de celdas de máxima longitud.

Double Back es un rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. El objetivo es trazar una línea cerrada a través de todas las celdas blancas para que la línea visite cada región dos veces. La línea no debe entrecruzarse. La cuadrícula puede contener celdas negras; la línea no debe pasar a través de estas celdas.

Wamuzu (pronunciación japonesa de la expresión inglesa “Worms”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Consta de una cuadrícula que contiene círculos en algunas celdas. El objetivo es conectar todos los círculos en pares con líneas, cumpliendo con las siguientes condiciones:

• Sólo se puede dibujar una línea a través de una celda; ésta debe pasar por el centro de la celda.
• Las líneas pasan por todas las celdas de la cuadrícula.
• La longitud de cada sección de la línea no debe ser mayor que el lado de la celda.

Kaero (“Ouchihekaero”; del japonés “vamos a casa”) es un rompecabezas de lógica creado por Naoki Inaba de Japón. Una cuadrícula cuadrada o rectangular dividida en regiones contiene letras en algunas celdas. El objetivo es mover algunas letras de tal forma que cada región contenga las mismas letras. La letra se mueve a lo largo de la cuadrícula de manera aleatoria, cambiando la dirección del movimiento horizontal y verticalmente. Por cada celda debe pasar el camino de no más de una letra (algunas celdas pueden permanecer vacías). Los caminos que siguen las letras no pueden cruzarse ni pasar por encima de otras letras.

Kapama (del turco “cierre”) es una variedad de rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene líneas diagonales en algunas celdas. El objetivo es pintar algunas celdas para obtener figuras emparejadas conectadas por líneas diagonales. Las figuras emparejadas deben ser simétricas con respecto a la línea diagonal. Las figuras no deben tocarse entre sí por los lados. Las celdas con líneas diagonales no se pueden pintar. Los números fuera de la cuadrícula muestran cuántas celdas están pintadas en la fila o columna correspondiente.

Yunikumaka (pronunciación japonesa de la expresión inglesa “Unique Marker”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Hay puntos ubicados dentro de una cuadrícula cuadrada o rectangular. Cada punto puede estar en el centro de una celda o en el borde entre celdas vecinas. El objetivo es dividir la cuadrícula en regiones de cuatro celdas (tetrominós). Cada región debe contener un punto (en el centro de la celda o en el borde entre celdas dentro de la región). Se ignoran los puntos en la frontera entre regiones. La cuadrícula puede contener celdas negras que no pertenecen a ninguna de las regiones.

Meandering Numbers (“Count Number”, “Worms”) consta de una cuadrícula cuadrada o rectangular dividida en regiones. Algunas regiones pueden tener números dentro. El objetivo es llenar cada región con números del 1 al N, donde N es el tamaño de la región. Los números dentro de una región representan un camino: hay que ir del 1 al N moviéndose de celda en celda horizontal o verticalmente. Los números idénticos en la cuadrícula no deben tocarse, ni siquiera en diagonal.

Yokibunkatsu (del japonés: “hacer patrón de contenedor”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Una cuadrícula cuadrada o rectangular contiene estrellas en algunas celdas. El objetivo es dividir la cuadrícula en regiones de 5 celdas para que cada región contenga una estrella. Las celdas de la región representan el despliegue de un cubo (“caja”), que se puede plegar de tal manera que la estrella esté en la parte inferior del cubo y el cubo no tenga una cara superior (“tapa”) . Algunos bordes entre regiones pueden estar definidos en la cuadrícula. El rompecabezas puede contener celdas que no pertenecen a ninguna de las regiones.

Scrin (pronunciación japonesa de la palabra inglesa “Screen”) es una variación de rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene círculos vacíos y círculos con números en algunas celdas. El objetivo es colocar regiones cuadradas o rectangulares en la cuadrícula de tal forma que cada celda con un círculo quede dentro de una región. Una región no debe contener más de un círculo. La cuadrícula puede contener regiones sin círculos. El número indica la cantidad de celdas que contiene la región. Una región sin un número o una región con un círculo vacío puede tener cualquier tamaño. Las regiones sólo pueden tocarse en diagonal. Todas las regiones forman un bucle y se tocan entre sí con las esquinas.

De 1 a X (“From 1 To X”) es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. El objetivo es llenar todas las celdas con números para que cada región contenga números del 1 al de la cantidad de celdas en la región. Dos celdas adyacentes no pueden contener los mismos números. El número fuera de la cuadrícula indica la suma de todos los números en la fila o columna correspondiente.

Shingoki (del japonés “semáforo”) es un rompecabezas lógico de forma cuadrada o rectangular, en algunas celdas del cual hay círculos (con o sin números). El objetivo es trazar una línea cerrada a través de todos los círculos en la cuadrícula; la línea no tiene que pasar por todas las celdas de la cuadrícula. La línea no debe entrecruzarse. La línea ha de pasar recta por los círculos blancos. Cuando la línea cruza el círculo negro, debe girar 90 grados. La línea puede pasar por los círculos grises de cualquier forma. Si un círculo contiene un número, representa la longitud total de las líneas rectas que salen de ese círculo.

Stitches es una variación de rompecabezas de lógica. Una cuadrícula cuadrada o rectangular se divide en regiones. El objetivo es conectar cada par de regiones vecinas con una línea recta de una celda de largo (los extremos de la línea deben estar en celdas adyacentes). Una celda no puede contener más de una línea. El número fuera de la cuadrícula indica cuántos extremos de línea deben colocarse en la fila o columna correspondiente.

Cross+A puede resolver rompecabezas en los que las regiones vecinas deben estar conectadas con 2, 3 o 4 líneas.

Neibadomino (pronunciación japonesa de la expresión inglesa “Neighbour Domino”) es un rompecabezas lógico inventado por Naoki Inaba de Japón. Una cuadrícula cuadrada o rectangular contiene números en algunas celdas. El objetivo es colocar bloques de dos celdas de tamaño (“dominó”) en la cuadrícula y llenarlos con números. No todas las celdas deben estar ocupadas por bloques. Cada celda con un número ha de pertenecer a un bloque. El número indica cuántos bloques están en contacto con este bloque horizontal y verticalmente (cuántos “vecinos” tiene este bloque). Los bloques con el mismo número de vecinos no pueden ser vecinos. Cada área de 2 x 2 debe contener al menos una celda que no pertenezca a ninguno de los bloques. Se permiten zonas de 2 x 2 en las que las celdas no pertenecen a ninguno de los bloques.

Jemini ("Jemini Block") es un rompecabezas de lógica inventado por Naoki Inaba de Japón. Una cuadrícula cuadrada o rectangular contiene letras en algunas celdas. El objetivo es dividir la cuadrícula en regiones para que cada región contenga solo una letra. En regiones que tienen el mismo tamaño, forma y orientación, la misma letra debe aparecer en la misma posición.

Double Choco es una variación de rompecabezas de lógica. La mitad de las celdas de la cuadrícula cuadrada o rectangular son de color gris. El objetivo es dividir la cuadrícula en regiones para que cada región contenga la misma cantidad de celdas blancas y grises. Dentro de una región, el área de celdas blancas y el área de celdas grises deben tener el mismo tamaño y forma (las áreas se pueden rotar o reflejar). La cuadrícula puede contener celdas con números: el número indica cuántas celdas del mismo color hay dentro de la región. Una región puede contener cualquier cantidad de celdas con números (los números deben ser iguales).

Konarupu (pronunciación japonesa de la expresión inglesa “Corner Loop”) es un rompecabezas lógico inventado por Naoki Inaba de Japón. El objetivo es trazar una línea cerrada a través de los puntos de la cuadrícula cuadrada o rectangular. La línea no debe entrecruzarse. El número indica cuántas veces la línea gira 90 grados en puntos adyacentes al número.

Gaidoaro (pronunciación japonesa de la expresión inglesa “Guide Arrow”) es un rompecabezas de lógica inventado por Naoki Inaba de Japón. La cuadrícula cuadrada o rectangular contiene flechas y una estrella. El objetivo es pintar algunas celdas de negro para que todas las celdas blancas estén conectadas entre sí horizontal y verticalmente. Las celdas con flechas o estrella no se pueden pintar. No se puede pintar dos celdas que tengan un borde común. Las flechas indican la dirección del camino a lo largo de las celdas blancas hasta la celda con la estrella (solo hay un camino posible desde cada celda blanca hasta la celda con la estrella).

Mid-Loop es una variación de rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene puntos. Cada punto puede estar en el centro de una celda o en el borde entre celdas vecinas. El objetivo es trazar una línea cerrada que no debe entrecruzarse a través de todos los puntos. La línea no tiene que pasar por todas las celdas de la cuadrícula. La línea debe pasar recta por los puntos. Los segmentos de línea que parten de un punto deben ser iguales.

Dotchi-Loop es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. Es necesario trazar una línea cerrada que no debe entrecruzarse. La línea debe cruzar todas las celdas con círculos blancos y no debe pasar por las celdas con círculos negros. Dentro de una región, la línea debe pasar recta a través del círculo blanco o girar 90 grados en el círculo blanco.

Trinairo es un rompecabezas de lógica creado por Leo de Winter de los Países Bajos. Consta de una cuadrícula de 9 x 9 con letras en algunas celdas. El objetivo es llenar todas las celdas con letras para que en cada fila y cada columna haya tres letras A, tres letras B y tres letras C. Si una celda está resaltada con un color diferente, la letra en dicha celda no debe coincidir con las letras de las celdas vecinas horizontal y verticalmente (solo algunas de estas celdas están marcadas en la cuadrícula).

Detour es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. El objetivo es trazar una línea cerrada a través de todas las celdas de la cuadrícula. La línea no debe entrecruzarse. El número indica cuántas veces la línea debe girar dentro de la región. Si la región no contiene un número, la línea puede realizar cualquier cantidad de giros.

Balance Loop es una variedad de rompecabezas lógico inventado por Prasanna Seshadri de la India. Una cuadrícula cuadrada o rectangular contiene círculos blancos y negros. El objetivo es trazar una línea cerrada a través de todas las celdas con círculos. La línea no debe entrecruzarse. Del círculo blanco deben salir segmentos de línea de igual longitud (la longitud se mide desde el círculo hasta el giro más cercano de la línea). Del círculo negro deben salir segmentos de diferentes longitudes. El número dentro del círculo es igual a la suma de las longitudes de los segmentos de línea que salen de este círculo.

Turf es un rompecabezas lógico inventado por John Bulten de EE.UU. Algunas celdas de una cuadrícula cuadrada o rectangular contienen números. El objetivo es dividir la cuadrícula en regiones blancas y grises, pintando algunas de las celdas de gris. En cada región, uno de los números debe ser igual a la cantidad de celdas en la región. Los números restantes dentro de la región indican la cantidad de celdas blancas alrededor de la celda con el número (incluida esta celda misma).

SquarO es un rompecabezas cuyas reglas son similares a las del rompecabezas Minesweeper. En una cuadrícula cuadrada o rectangular, los puntos se ubican en las intersecciones de líneas. El objetivo es pintar algunos de los puntos. El número dentro de una celda significa la cantidad de puntos pintados alrededor de esa celda.

Chiyotsui (del japonés, “bisagra de puerta”) es un rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. El objetivo es pintar algunas celdas de tal manera que se creen áreas de celdas negras que solo pueden tocarse entre sí en diagonal. Cada área de celdas negras se encuentra en dos regiones diferentes y consta de dos mitades, simétricas con respecto al borde de la región. El número dentro de la región indica cuántas celdas se deben pintar. Si no hay ningún número, se puede pintar cualquier cantidad de celdas (todas las celdas de la región pueden permanecer blancas).

Aqre es un rompecabezas lógico inventado por Eric Fox de EE.UU. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. El objetivo es pintar algunas celdas de tal manera que todas las celdas negras estén conectadas entre sí horizontal o verticalmente. El número indica cuántas celdas se deben pintar dentro de la región. En una región sin número, se puede pintar cualquier cantidad de celdas (todas las celdas de la región pueden permanecer blancas). Solo se pueden pintar o no tres celdas seguidas horizontal o verticalmente.

Geradeweg ("Straight Loop") es una variación de rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular, algunas celdas de la cual contienen círculos con números. El objetivo es trazar una línea cerrada a través de todas las celdas con círculos. La línea no debe entrecruzarse. El número indica la longitud del segmento de la línea que pasa por el círculo. Si una línea gira en una celda con un círculo, ambos segmentos de línea deben tener la longitud igual al número en el círculo.

Kuroclone es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. El objetivo es pintar algunas celdas de tal manera que se creen áreas de celdas negras que solo pueden tocarse entre sí en diagonal. Cada región ha de contener dos áreas de celdas negras: estas áreas deben tener el mismo tamaño y forma (las áreas se pueden rotar o reflejar). Algunas celdas tienen números con flechas; dichas celdas siempre deben permanecer blancas. La flecha apunta a una celda adyacente que pertenece a una de las áreas de celdas negras. El número indica la cantidad de celdas de esta área. Si dos celdas adyacentes están separadas por un borde de región, una de las celdas debe ser blanca.

Yajisan-Sokoban es un rompecabezas de lógica inventado por Jamie Hargrove. Una cuadrícula cuadrada o rectangular contiene cuadrados grises en algunas celdas, así como celdas con números y flechas. El objetivo es mover los cuadrados grises horizontal o verticalmente (algunos cuadrados pueden quedar en su lugar). Los caminos que toman los cuadrados grises no pueden cruzarse ni atravesar otros cuadrados grises (pero pueden pasar por cuadrados con números). El número indica cuántos cuadrados grises se ubicarán en la dirección que apunta la flecha. Si el cuadrado gris después de moverse se encuentra encima del número con flecha, la información de esta celda se ignora (puede ser tanto verdadera como falsa). Si el camino del cuadrado gris cruza una celda con el número, la información de dicha celda es verdadera.

Line Segment es un rompecabezas lógico inventado por Erich Friedman de EE.UU. El objetivo es llenar una cuadrícula cuadrada o rectangular con líneas de 3 o 4 celdas de largo. La línea puede ser horizontal (H), vertical (V) o diagonal (D). Sólo una línea ha de atravesar cada celda de la cuadrícula. La letra en una celda indica el tipo de línea que pasa por esa celda.

Raneko (“Ranekomappu”; del japonés: “mapa de lugares donde viven los gatos”) es una variedad de rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular, en algunas celdas de las cual hay círculos (con números o vacíos). El objetivo es dividir la cuadrícula en regiones de forma aleatoria para que cada región contenga un círculo (un “gato”). El número en el círculo indica la cantidad de celdas en la región. La región con un círculo vacío puede ser de cualquier tamaño. La cuadrícula puede contener celdas negras que no pertenecen a regiones. Si hay un número en una celda negra, indica cuántas regiones son adyacentes a esta celda horizontal y verticalmente.

Factorism ("Find the Factors") es un rompecabezas lógico inventado por Iva Sallay de EE.UU. El objetivo es colocar los números del 1 al N en la parte superior e izquierda de una cuadrícula cuadrada de tamaño N x N. El número en la celda es el producto de los números fuera de la cuadrícula en la fila y columna correspondientes.

Akiperago (pronunciación japonesa de la palabra inglesa “Archipelago”) es un rompecabezas de lógica. La cuadrícula cuadrada o rectangular contiene celdas negras, algunas de las cuales contienen números. El objetivo es pintar las celdas de negro, cumpliendo con las siguientes reglas:

• Las celdas negras forman “islas” de forma aleatoria. Dos islas cualesquiera pueden tocarse sólo con sus esquinas.
• El número indica la cantidad de celdas en la isla. La isla puede contener varias celdas con números (en este caso los números serán los mismos).
• Todas las islas forman “archipiélagos”. Un archipiélago es un grupo de dos o más islas que se tocan en las esquinas.
• Si un archipiélago contiene N islas, tendrán entre 1 y N celdas (no necesariamente en ese orden).

Yakazu consta de una cuadrícula cuadrada o rectangular con algunas celdas de color negro. El objetivo es poner los números en las celdas blancas de tal manera que se formen conjuntos de números consecutivos en los espacios entre las celdas negras, pero no necesariamente en orden ascendente o descendente (por ejemplo, 3-1-2-4). Toda secuencia de dos o más números debe comenzar con el número 1.

Miraringutairu (pronunciación japonesa de la expresión inglesa “Mirroring Tile”) es un rompecabezas de lógica. En una cuadrícula cuadrada o rectangular, algunas celdas son de color negro. El objetivo es pintar las celdas negras para que formen bloques. Si una celda negra contiene número, es igual a la cantidad de celdas en el bloque (un bloque puede contener varias celdas con números). Los bloques no deben tocarse entre sí con los bordes. Cada bloque debe tocar al menos un bloque del mismo tamaño y forma (los bloques se pueden rotar o reflejar).

Heyablock ("Heyawake-Block") es un rompecabezas de lógica inventado por Atsumi Hirose (Japón). Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. El objetivo es pintar algunas celdas, cumpliendo con las siguientes reglas:

• Las celdas pintadas dentro de la misma región deben tocarse entre sí horizontal o verticalmente.
• El número indica cuántas celdas se deben pintar dentro de la región.
• En una región sin número, se puede pintar cualquier cantidad de celdas (al menos una celda).
• Si dos celdas adyacentes están separadas por un borde de región, una de las celdas debe ser blanca.
• Todas las celdas blancas deben estar conectadas entre sí horizontal o verticalmente.
• Una línea continua de celdas blancas no debe cruzar más de un borde de región.

Choco Banana es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene números en algunas celdas. El objetivo es pintar algunas celdas de la cuadrícula para crear áreas de celdas blancas y negras. Todas las áreas de las celdas negras deben tener forma cuadrada o rectangular. Todas las áreas de celdas blancas no deben ser cuadradas ni rectangulares. Si hay un número dentro de un área (pintada o sin pintar), debe ser igual a la cantidad de celdas en el área. Un área puede contener varios números iguales o no tener ninguno.

Wataridori (del japonés: “pájaro de paso”) es una variación de rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. Algunas celdas de la cuadrícula tienen círculos (con números o vacíos). El objetivo es conectar todos los pares de círculos con líneas. Se puede trazar una línea entre círculos con los mismos números, entre círculos vacíos o conectar un círculo vacío y un círculo con número. Las líneas no deben cruzarse. Como máximo se puede trazar una línea a través de cada celda. El número en la celda indica cuántas regiones debe visitar la línea. Una línea sólo puede visitar una región una vez.

Chenburo (pronunciación japonesa de la expresión “Chain Block”) es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene celdas negras, algunas de las cuales contienen números o signos de interrogación. El objetivo es pintar las celdas de negro, cumpliendo con las siguientes reglas:

• Las celdas negras forman bloques de formas aleatorias. Dos bloques cualesquiera solo pueden tocarse en sus esquinas.
• El número indica el tamaño del bloque. Si un bloque contiene una celda con un signo de interrogación, el tamaño del bloque puede ser cualquiera.
• Cada bloque contiene un número o un signo de interrogación.
• Todos los bloques forman “cadenas”. Una cadena es un grupo de dos o más bloques que se tocan en las esquinas.
• Una cadena no puede contener dos bloques del mismo tamaño y forma (independientemente de cómo se giren o reflejen los bloques).

Wanrumuwandoa (pronunciación japonesa de la expresión inglesa “One Room One Door”) es una variación de rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. El objetivo es pintar algunas celdas, cumpliendo con las siguientes reglas:

• El número en una celda indica cuántas celdas hay que pintar de negro en esa región. Si una región no contiene un número, se puede pintar cualquier cantidad de celdas de esa región.
• Las celdas negras no pueden tocarse entre sí ni horizontal ni verticalmente.
• Las celdas negras no pueden dividir una región en varias áreas blancas.
• Entre regiones vecinas no debe haber más de un par de celdas blancas, separadas por un borde de región (no más de una “puerta”).
• Todas las celdas blancas deben estar conectadas entre sí horizontal o verticalmente.

Haisu (pronunciación japonesa de la palabra inglesa “House”) es un rompecabezas lógico inventado por William Hu. Una cuadrícula cuadrada o rectangular se divide en regiones de forma aleatoria. Es necesario trazar una línea (“camino”) desde la celda con la letra S (start) hasta la celda con la letra G (goal). La línea debe atravesar todas las celdas y no debe entrecruzarse. Si el camino pasa por una celda con un número dentro de una región, este número indica la vez que la línea visita la región. Si una región contiene un número escrito en letra pequeña, ese número representa cuántas veces la línea debe visitar esa región.

Obitaru (pronunciación japonesa de la palabra inglesa “Orbital”) consta de una cuadrícula que contiene círculos blancos y negros. El objetivo es dibujar caminos cerrados cuadrados o rectangulares (“órbitas”) que pasen por todos los círculos blancos. Los caminos pueden cruzarse entre sí, pero no pueden correr paralelos a través de la misma celda. Puede haber caminos que no pasen por ningún círculo blanco. El círculo negro debe estar dentro de una órbita. Si un círculo negro contiene un número, será igual al número de círculos blancos por los que pasa la órbita alrededor de ese círculo negro.

Square Jam es un rompecabezas de lógica. Una cuadrícula cuadrada o rectangular contiene números en algunas celdas. El objetivo es dividir la cuadrícula en regiones cuadradas. Si la región contiene un número, representa la longitud del lado del cuadrado. Una región puede contener varios números idénticos. Puede haber regiones sin números. No debe haber un punto en la intersección de las líneas de la cuadrícula donde se unan las esquinas de cuatro regiones diferentes.

Cocktail Lamp (pronunciación japonesa de la expresión inglesa “Cocktail Lamp”) es una variación de rompecabezas de lógica. Consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. El objetivo es pintar algunas celdas, cumpliendo con las siguientes reglas:

• Las celdas pintadas dentro de la misma región deben tocarse horizontal y verticalmente (formar el mismo bloque).
• El número indica cuántas celdas se deben pintar dentro de la región.
• En una región sin número, se puede pintar cualquier cantidad de celdas (todas las celdas de la región pueden quedar blancas).
• Si dos celdas adyacentes están separadas por un borde de región, una de las celdas debe ser blanca.
• Todos los bloques de celdas negras deben estar conectados entre sí en diagonal.
• No debe haber un área de 2 x 2 formada por celdas negras.

Kazoku (“Kazoku shashin”; del japonés “foto de familia”) es una variación de rompecabezas de lógica. La cuadrícula cuadrada o rectangular contiene círculos negros; algunos círculos pueden contener también números o signos de interrogación. Algunas celdas también pueden contener números o signos de interrogación. El objetivo es dividir la cuadrícula en regiones rectangulares. Cada región debe contener un número o un signo de interrogación. El número en la celda o en el círculo muestra cuántos círculos negros hay dentro de la región. Si hay un signo de interrogación en una celda o en un círculo, la región puede contener cualquier número de círculos negros (al menos uno). Si dos círculos negros están en celdas adyacentes horizontal o verticalmente, estos círculos están dentro de la misma región.

Tontonbeya (del japonés: “jugador azaroso”) consta de una cuadrícula cuadrada o rectangular dividida en regiones de forma aleatoria. El objetivo es colocar una de las tres figuras (cuadrado, círculo o triángulo) en cada celda, cumpliendo con las siguientes reglas:

• Una región puede contener cualquier figura, pero si contiene diferentes símbolos, entonces debe haber cantidades iguales de cada tipo de figura.
• Las celdas con las mismas figuras dentro de la misma región deben tocarse horizontal y verticalmente (formar un mismo bloque).
• Cada bloque de figuras idénticas dentro de una región debe ser adyacente a un bloque de las mismas formas en otra región. No debe haber un bloque de figuras que sea adyacente a dos o más bloques de las mismas figuras en otras regiones.

Contexto ("Context") consta de una cuadrícula cuadrada o rectangular con números en algunas celdas. El objetivo es pintar las celdas de negro para que todas las celdas blancas estén conectadas entre sí horizontal y verticalmente. La celda con el número puede ser pintada. No se pueden pintar dos celdas que tengan un borde común. El número en una celda blanca indica la cantidad de celdas negras vecinas que tienen un borde común con esta celda. El número en una celda negra significa la cantidad de celdas negras adyacentes en diagonal.

Word Finder ("Word Search", "Word Seek", "Word Sleuth", "Mystery Word") es una cuadrícula con letras de forma rectangular o cuadrada. Hay que encontrar las palabras escondidas en la cuadrícula con letras. Las palabras se leen en una línea quebrada; la línea puede doblarse sólo en ángulo recto. Cada letra se puede usar sólo en una palabra.

Para crear un rompecabezas hay que hacer una lista de palabras. También se puede indicar una palabra clave compuesta de las letras que queden después de resolver el rompecabezas.

Nueve letras ("Nine Letters") es una variedad del rompecabezas Word Finder. Es una cuadrícula con letras, dividida en regiones de 3 x 3. Hay que encontrar palabras de 9 letras escondidas dentro de cada región.

Telaraña ("Spider Web") se compone de círculos unidos uno con el otro mediante líneas. En los círculos se encuentran letras, hace falta encontrar la secuencia continua de los círculos que posean letras de la palabra clave.

Laberinto ("Maze") es una estructura formada de caminos enredados. En pasatiempos de ese tipo hay que encontrar el camino entre dos puntos asignados. El programa permite crear laberintos de forma libre, no solamente rectangular o cuadrada.