Cross+A Variantes de rompecabezas

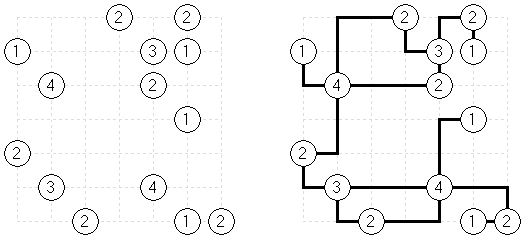
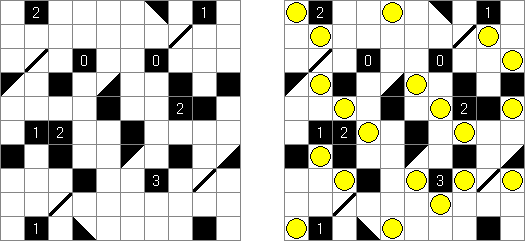
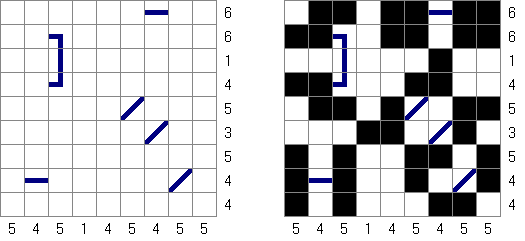
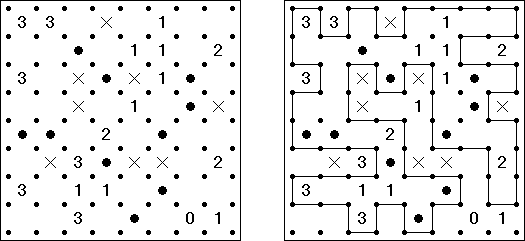
• Slitherlink
• Ovejas y lobos
• Batalla naval
• Digital Battleships
• Retrograde Battleships
• Fillomino
• No Rectangles Fillomino
• Only Rectangles Fillomino
• No 2 x 2 Squares Fillomino
• Non-Consecutive Fillomino
• Consecutive Fillomino
• No Row/Column Repeats Fillomino
• All Odds Fillomino
• All Evens Fillomino
• Nurikabe
• Line Nurikabe
• Parejas de Nurikabe
• Rascacielos
• Sum Rascacielos
• Tapa
• Tapa [En línea]
• Tapa sin cuadrados
• Tapa igual
• Tapa negra y blanca
• Tapa islas
• Pata
• Tapa balanza
• Tapa en fila
• Tapa 1-n
• Tapa partida
• Tapa [Diagonal Neighbors]
• Corral
• Dentro/Fuera de Corral
• Arukone
• Arukone³
• ABC
• Not as Easy as ABC
• Ichimaga
• Crossing Ichimaga
• Magnetic Ichimaga
• Snake
• Multiple Snakes
• Toroidal Snake
• Buscaminas
• Double Minesweeper
• Mirukuti
• Milk Tease
• Akari
• Mirror Akari
• Tren
• Tren+
• Ghost Tren
• Mubunanba
• Mubunanba+
• Yajilin
• Regional Yajilin
• LITS
• Double LITS
• Kapama
• Sunglasses
• Makaro
• Masakuchi

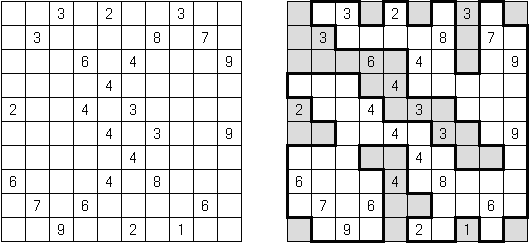
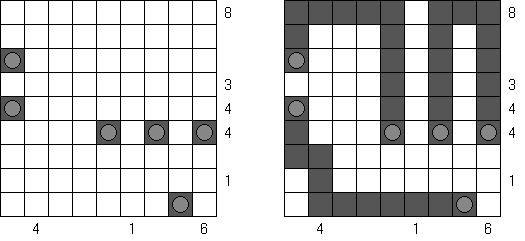
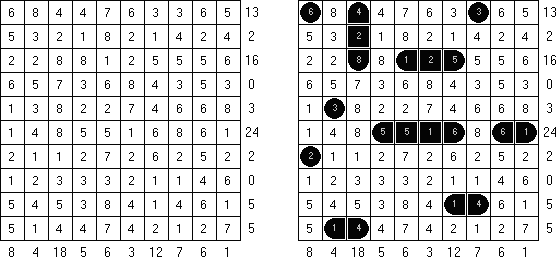
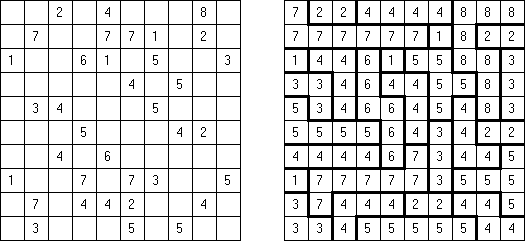
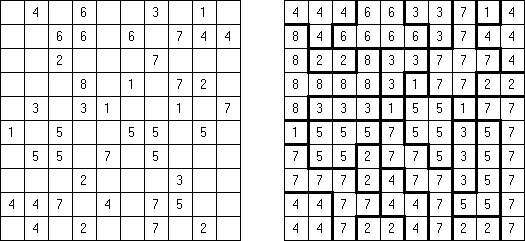
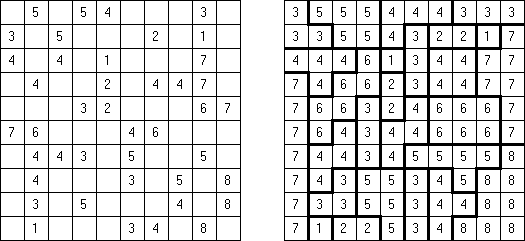
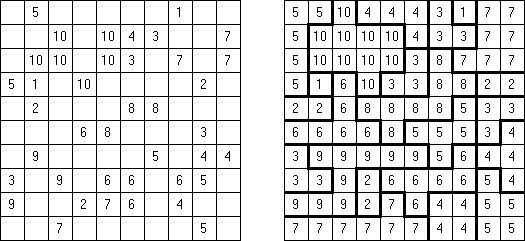
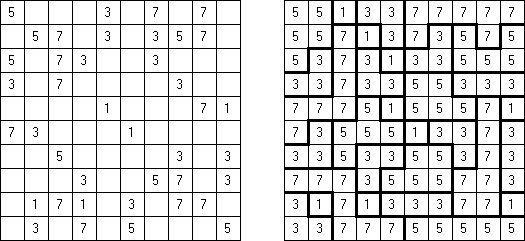
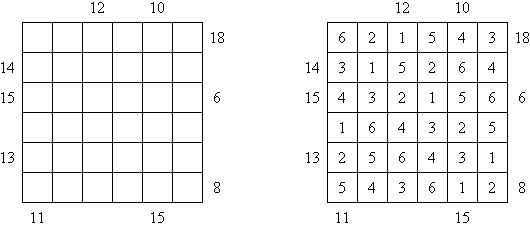
Ovejas y lobos ("Sheep and Wolves") es una variedad del rompecabezas Slitherlink: además de los dígitos del 0 al 3, contiene también círculos negros ("ovejas") y cruces negras ("lobos"). Al final de la resolución del rompecabezas las "ovejas" deben quedar dentro de una línea cerrada ("dentro del corral") y los "lobos" fuera de la línea cerrada ("fuera del corral").

In Digital Battleships all cells of the grid contain numbers. The values on the right and bottom edges of the grid reveal the sum of the numbers in each of the ship pieces that appear in each respective row or column.

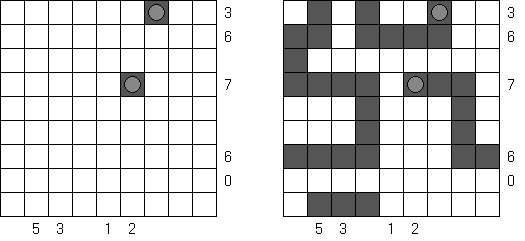
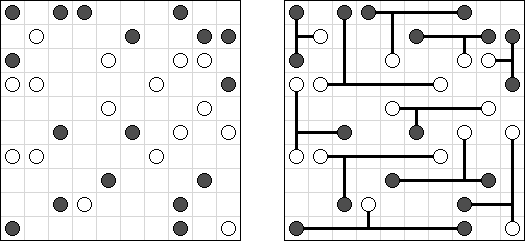
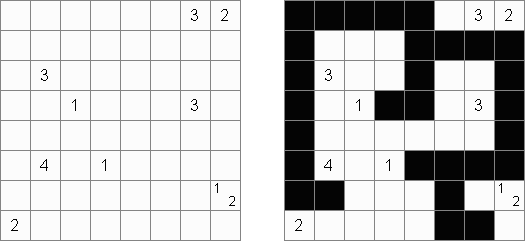
Retrograde Battleships ("Reverse Battleships") contains all segments of the ships in the grid. The aim is to find the correct locations of the ships. No ship may touch another, even diagonally.

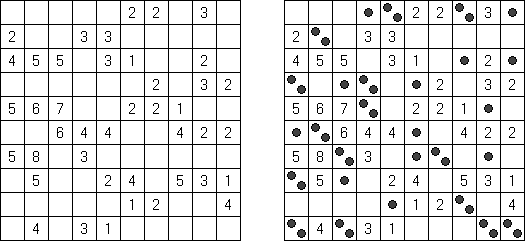
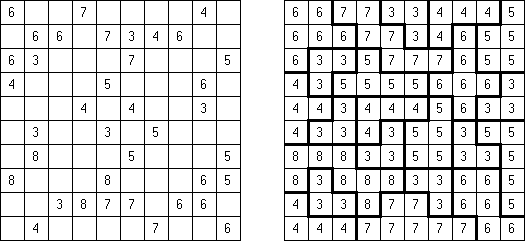
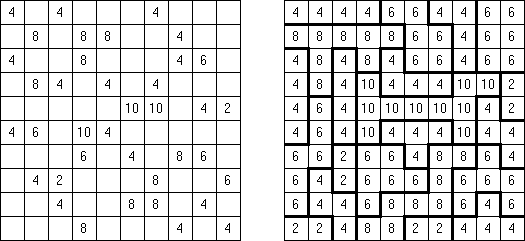
No Rectangles Fillomino tiene regla adicional: ninguno de los bloques deben tener una forma rectangular o cuadrada.

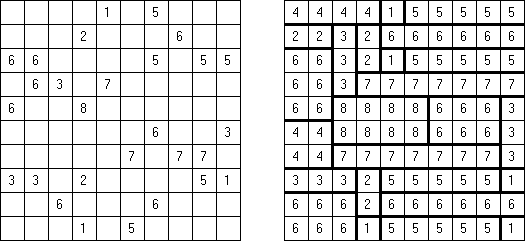
Only Rectangles Fillomino: todos los bloques deben ser rectangulares o cuadrados.

No 2 x 2 Squares Fillomino: en la cuadrícula no debe haber áreas de 2 x 2 que contenga números iguales.

Non-Consecutive Fillomino: las casillas de dos bloques que se tocan horizontal o verticalmente no deben diferir por uno.

Consecutive Fillomino: cada bloque debe tocar horizontal o verticalmente con al menos un bloque cuyo tamaño se diferencia en una casilla.

No Row/Column Repeats Fillomino ("Deadomino"): todos los números iguales en una fila o columna deben pertenecer al mismo bloque. Por ejemplo, si se repiten dos veces los "5", ambos pertenecen al mismo bloque.

All Odds Fillomino: los tamaños de todos los bloques son números impares.

All Evens Fillomino: los tamaños de todos los bloques son números pares.

Line Nurikabe: a grid cannot contain five consecutive black cells in a row or column (2 x 2 cell area can be all black).

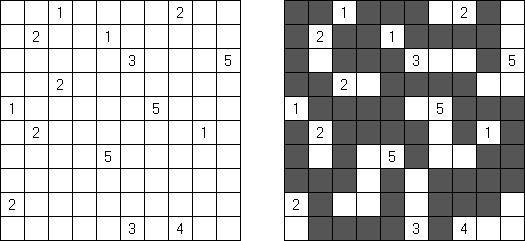
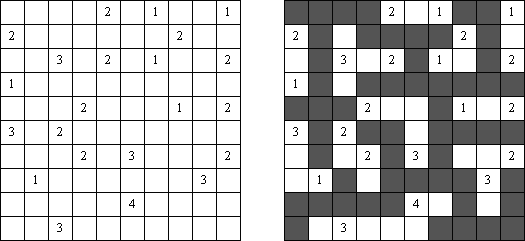
Parejas de Nurikabe ("Pairs Nurikabe") se diferencia del Nurikabe trivial en que cada isla contiene dos números y su suma es igual al superficie de la isla.

Sum Rascacielos ("Sum Skyscrapers") se diferencia de Rascacielos ("Skyscrapers") en que los números fuera de la cuadrícula significan las sumas de pisos de las casas y no cantidad de casas visibles.

Existen muchas variedades del rompecabezas de Tapa. El programa Cross+A sabe solucionar unas de estas.

Tapa [En línea] ("Tapa [Line]") se basa en la regla adicional: No se puede formar una línea horizontal o vertical de cuatro celdas negras.

Tapa sin cuadrados ("No Squares Tapa"): no se permite formar cuadrados blancos de 2 a 2 celdas.

Tapa igual ("Equal Tapa"): la cantidad de celdas blancas (las celdas con números se excluyen) es igual a la catidad de celdas negras.

Tapa negra y blanca ("B&W Tapa"):

• Todas las celdas blanas forman una zona integra.
• No se permite formar cuadrados blancos o negros de 2 a 2 celdas.
• Las celdas con números son blancas.

Tapa islas ("Tapa Islands"):

• Los grupos de celdas blancas forman zonas separadas ("islas").
• En cada zona blanca no puede estar más de una celda con número.
• Un número de números en la celda es igual a la superficie de la "isla".
• Se puede dejar unas zonas blancas sin celdas con números.

Pata:

• Los números en una celda significan zonas integras de celdas blancas en torno de la celda.
• Las zonas de celdas blancas se separan por una celda negra o más.

Tapa balanza ("Tapa Balance"): la cantidad de celdas negras en la parte izquierda de la malla es igual a la cantidad de las celdas negras en la parte derecha. La celdas blancas y celdas con números no se toman en cuenta.

Tapa en fila ("Tapa Row"): la suma de números en cada fila es igual a la cantidad de celdas negras en esta fila.

Tapa 1-n: todos columnas y filas deben contener el número diferente de celdas negras.

Tapa partida ("Dissected Tapa"): celdas blancas y celdas negras forman dos figuras congruentes. Es que estas figuras coinciden al sobreponerlas.

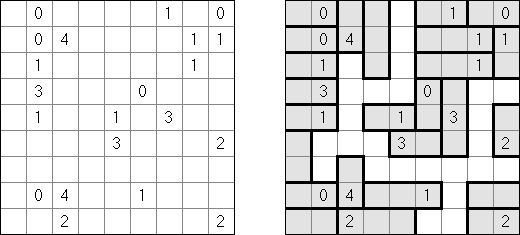
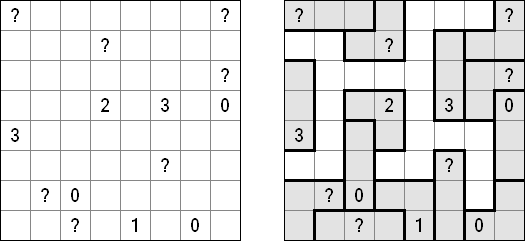
Tapa [Diagonal Neighbors]: cada casilla negra debe tener por lo menos una casilla vecina negra en diagonal.

Dentro/Fuera de Corral ("Inside/Outside Corral") es una variedad de Corral. La diferencia es que numeros se situan dentro de la línea cerrada o fuera de esta. En ambos casos cada número es igual a la cantidad de las celdas "visibles" en horizontal y en vertical, incluida la misma celda.

Arukone³:

• Every line must not cover 2 x 2 area.
• All cells in the grid must be filled.

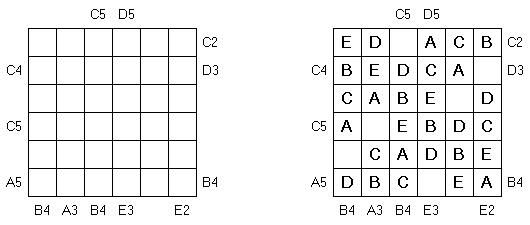
Not as Easy as ABC is a variation of Easy as ABC puzzle. The goal is to fill in the first letters of the alphabet on every row and every column exactly once. One cell in every row and every column remains empty. Letters and numbers on the outside indicate at what position you come across this letter when looking from that side (e.g. C₂ means the C is the second letter encountered when looking from that side).

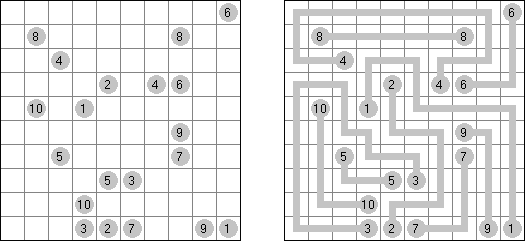
Crossing Ichimaga: the lines may cross other lines; the lines cannot change direction at the point of intersection.

Magnetic Ichimaga ("Jishaku-Ichimaga"): the circles with the same digits cannot be connected.

Multiple Snakes: a grid contains multiple snakes. Head and tail of all snakes are given. Different snakes do not touch each other, even diagonally.

Toroidal Snake: a grid wraps around itself. A snake can go from one edge to another.

Double Minesweeper: place mines into each empty cell in the grid, at most two mines per cell.

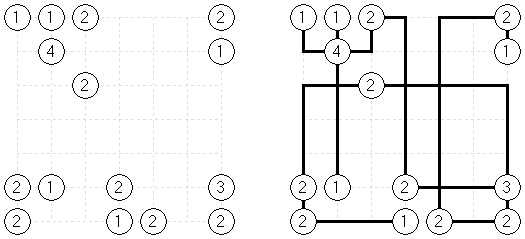
Milk Tease is a variation of Mirukuti ("Milk-T") puzzle. T-shaped line may connect:

• one black circle and two white circles;
• one white circle and two black circles.

Two circles of the same color must be connected by the straight-line segment of the T-shaped line.

Mirror Akari ("!irakAkari!"): a square or rectangular grid contains diagonal walls (black triangles) with mirrors.

• No two bulbs shine on each other, even by reflected light. A bulb cannot shine on itself.
• If a cell contains a diagonal wall ("mirror"), it should be lit.
• If a cell contains a diagonal line ("two-sided mirror"), both sides of a mirror should be lit.
• A cell with a mirror cannot contain a bulb.

Tren+:

• Each block contains exactly one number or a question sign (unknown number), indicating the amount of its possible movements.
• All cells that are not part of any block must be connected horizontally or vertically.

Ghost Tren:

• Blocks can also be placed without any numbers, with no restrictions on their ability to move.
• All cells that are not part of any block must be connected horizontally or vertically.

Mubunanba+:

• Each block contains exactly one digit or a question sign (unknown digit), indicating the number of possible directions to move a block.
• All cells that are not part of any block must be connected horizontally or vertically.

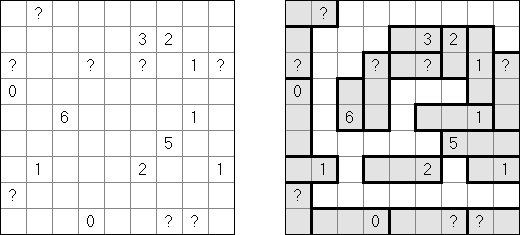
Regional Yajilin (also known as "Yajilin (Regions)") is a square or rectangular grid divided into regions. The aim is to blacken some cells and to draw a single non-intersecting loop through all the white cells. A number in a region indicates the number of black cells in that region. A region without a number can contain any amount of black cells. No two black cells can share a border. The loop may visit numbered cells; numbered cells can be blackened.

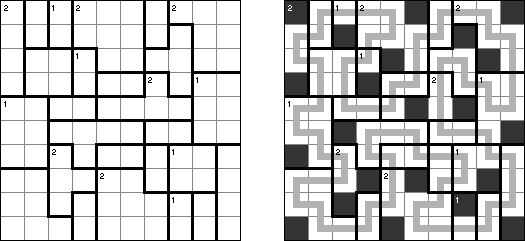
Double LITS has one difference from the classic variant of the puzzle: each region must contain two tetrominoes. These two tetrominoes within a region cannot touch each other horizontally or vertically (only diagonally); they can be the same or different shapes.

Sunglasses is a logic puzzle. A rectangular or square grid contains lines ("bridges") in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes ("lenses") are symmetrical with respect to a bridge. Two lenses may not share an edge. Cells with bridges can not be blacken. Numbers outside the grid show the number of black cells in a corresponding row or column.

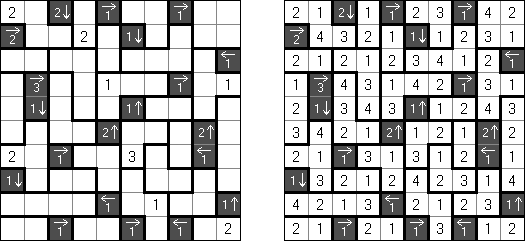
Masakuchi is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. The grid may contain black cells with arrows and numbers: the arrow points at the greatest number among the four cells around (up, under, left, right) the black cell. The number in the black cell shows the difference between the greatest number and the second highest number in all orthogonally adjacent cells around the black cell.